|
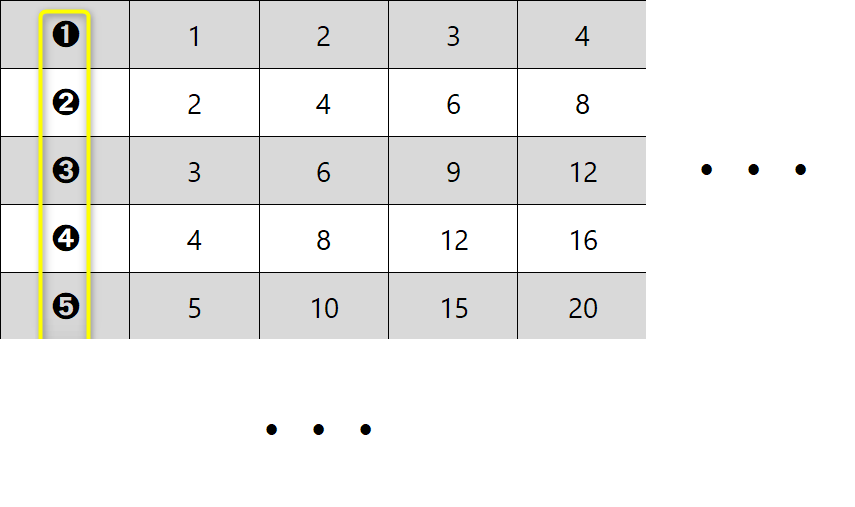
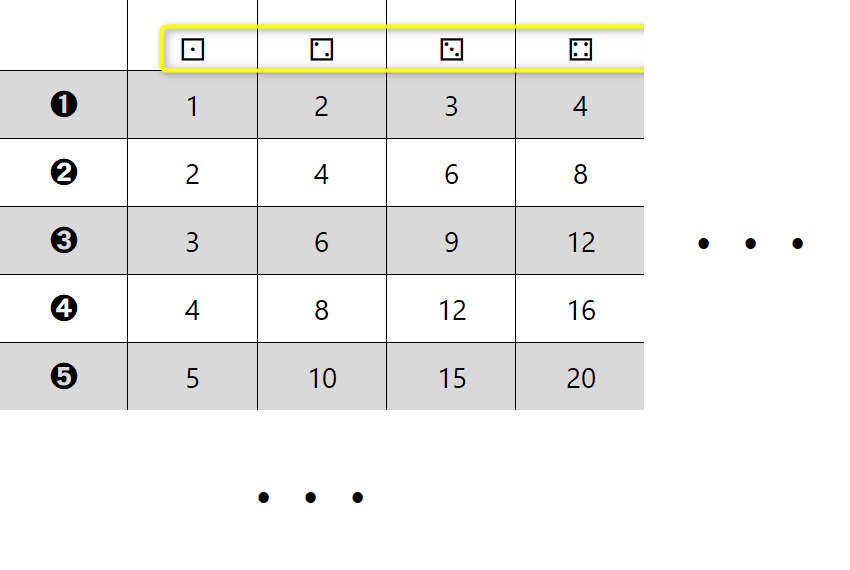
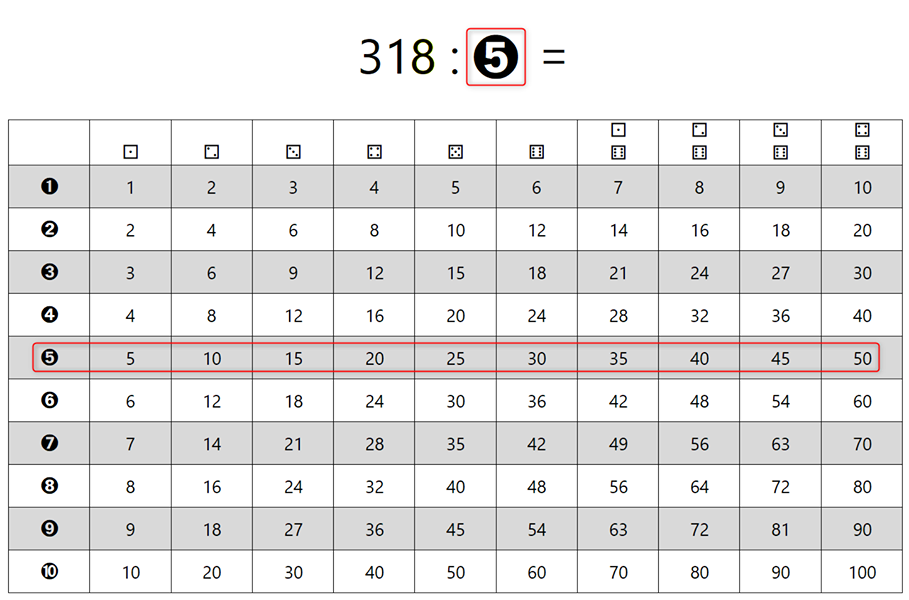
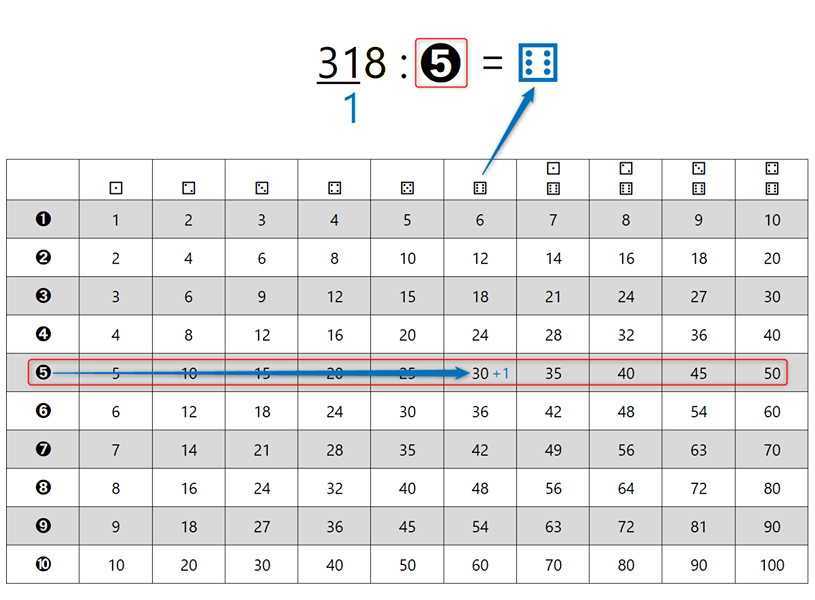
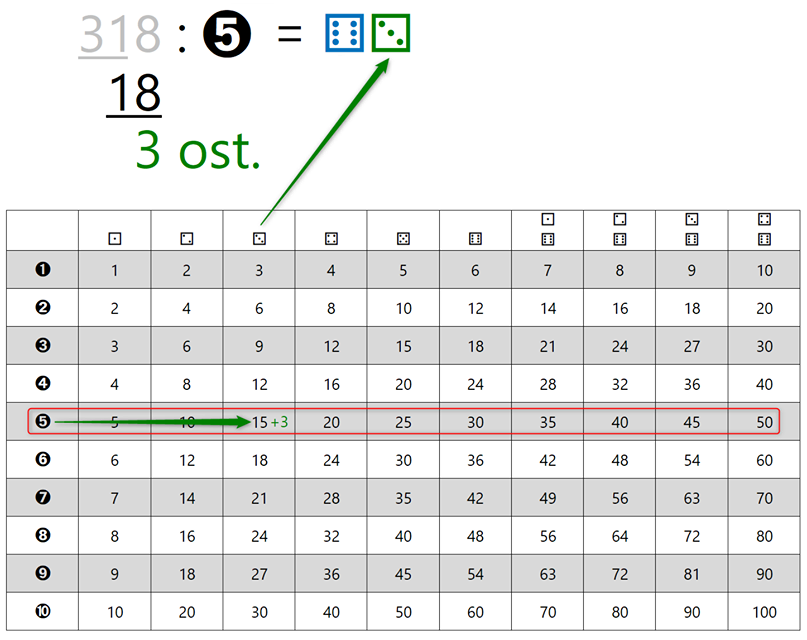
Naj vas najprej pomirim, tale pripomoček ni "potuha", če se je kdo slučajno ustrašil, je pa odličen "pomočnik" pri deljenju z ostankom in nam omogoča, da postopek tudi dejansko razumemo, ne le "znamo na pamet", kakor je na žalost dokaj pogosto pri poštevanki. Za 4 krat 5 vemo, da je 20, 20 deljeno s 4 pa je že problem. Kaj šele 21 deljeno s 4 ... Pri deljenju je ključno poznavanje večkratnikov delitelja (to je število, s katerim delimo oz. "tisto, kar stoji za dvopičjem" 😉). Zato celoten pripomoček temelji na večkratnikih števil. Zapišimo prvih 10 večkratnikov števil od 1 do 10 in sicer za vsako število v svojo vrstico tabele: Verjetno se vsi strinjamo, da se matematične pojme in postopke lažje zapomnimo, če jih povežemo z nečim znanim iz življenja. Nekaj takšnega so igralne kocke. Kot vemo, število pik pomeni vrednost, ki je "padla" ob metu kocke. Ena pika pomeni eno točko. Sedaj pa si predstavljajmo, da pika ni vredna eno točko, ampak več točk, od 1 do 10. To označimo tudi na naši tabeli - v prvi vrstici je pika vredna eno točko, v drugi dve in tako naprej do 10: Imena vrstic smo označili, preostanejo pa nam še imena stolpcev. Na podoben način, kot smo s številkami od 1 do 10 v krožcih označili vrstice, označimo tudi stolpce in sicer s kockami, na katerih je "padla" vrednost od 1 do 10. Ko na eni kocki "zmanjka pik", dodamo še eno kocko. Število pik na kocki pomeni, kateri večkratnik (po vrsti) števila v krožcu (v računu bo to delitelj) je zapisan v stolpcu pod kocko. Da bo razumevanje lažje, dodajmo še primer. Če na kocki padejo 4 pike (skrajno desni stolpec na sliki) in je vrednost posamezne pike 5 (spodnja vrstica na sliki), je skupna vrednost vseh pik 20, saj je 4 krat 5 enako 20. Velja seveda tudi, da je 20 deljeno s 4 enako 5 in 20 deljeno s 5 enako 4. Sedaj pa si oglejmo uporabo pripomočka na konkretnem računu deljenja z enomestnim številom, izračunajmo, koliko je 318 : 5. Ker delitelj (5) deli deljenca (318), bo iz deljenca nastalo več (enako velikih!) delčkov (in še nekaj ostanka). Število teh delčkov bomo zapisali desno od enačaja (to pa bo količnik). En tak delček je "vreden" 5 enot, ravno toliko, kot je "vreden" delitelj. "Po domače" nas zanima, koliko "petic" lahko "stlačimo" v škatlo, v katerem je prostora za 318 enot. Do rezultata najlažje pridemo tako, da poiščemo večkratnike delitelja, v našem primeru 5: Ker je 318 kar veliko število, bi morala biti spodnja tabela zelo široka, da bi v njej lahko našli rezultat. 🙂 Zato se reševanja lotimo postopoma. V vsakem koraku se bomo osredotočili le na prvih devet večkratnikov delitelja (dopustimo tudi 0), zato bo tabela z desetimi stolpci popolnoma dovolj. S tem postopkom v vsakem koraku dobimo eno števko rezultata oziroma količnika. Ker bomo račun reševali postopoma, je na začetku potrebno določiti, kolikšen del deljenca (318) bomo uporabili v prvem koraku. Izbiro začnemo z leve strani. Ker je vrednost prve števke (3) manj od 5 (delitelj), vzamemo prvi dve števki oziroma število 31. To število podčrtamo z vodoravno črto. Nadaljnji postopek pa je popolnoma enostaven:
Do sem je postopek dokaj standarden (morda le z izjemo načina označevanja stolpcev in vrstic v tabeli), medtem ko je naslednja ideja nekoliko bolj "smela". Pri prehodu na naslednji korak je potrebno določiti naslednji "mini" deljenec (v prejšnjem koraku je bilo to število 31 oziroma število, sestavljeno iz levih dveh števk števila 318). Običajno k ostanku v vrstici pod vodoravno črto (v našem primeru je to 1) prepišemo prvo števko od leve proti desni, ki ni podčrtana (v našem primeru je to 8) in dobimo naslednji "mini" deljenec 18. Naš predlog, ki bi si ga učenci verjetno lažje zapomnili, je naslednji: zakaj ne bi k ostanku v vrstici pod vodoravno črto "potisnili" kar celoten preostanek števila, ki ni podčrtan? V našem primeru je to sicer le števka 8, ampak če bi bil deljenec "daljši", bi pa lahko navzdol prestavili kar vse, kar ni podčrtano (trik: za lažje pomnjenje bi si predstavljali, da je delu deljenca "zmanjkalo tal pod nogami" 🙂 - to asociacijo bi si učenci lahko priklicali v spomin tudi, če bi postopek že nekoliko pozabili) S predlaganim pristopom je sicer v naslednjem koraku (in vsem, ki mu potencialno sledijo) potrebno znova določiti "mini" deljenca, a to ne bi smel biti prevelik problem saj za vse korake uporabimo enako logiko določevanja le-tega. Ponovimo postopek še za drugi "mini" deljenec (v našem primeru je to 18):
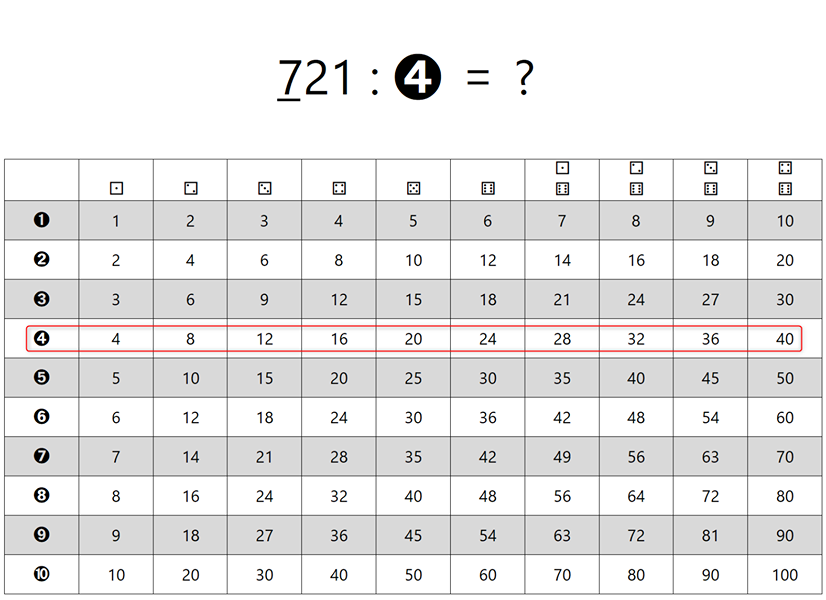
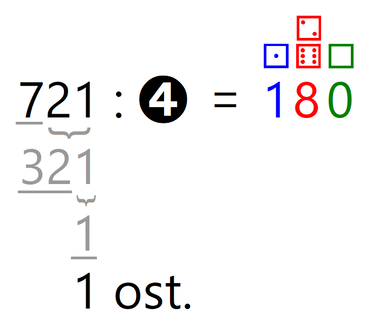
Ker desno od vodoravne črte ni nobene števke več (podčrtano je celotno število, s katerim smo delili oz. celoten "mini" deljenec, to je 18, zato nobeni števki ne more "zmanjkati tal pod nogami" 😉), smo z računanjem zaključili. Ostanek, ki smo ga dobili v zadnjem koraku deljenja (v našem primeru je to 3), je končni ostanek pri deljenju. Tega moramo v testu zapisati k rezultatu deljenja oziroma količniku, ki ga bomo iz kock "prebrali" pri zapisu končnega rezultata. Zapišimo še končni rezultat. Ostanek smo že določili, sedaj le še "preberimo" vrednosti kock. Število pik na kocki predstavlja vrednost posamezne števke, v našem primeru sta to 6 in 3, kar predstavlja število 63. V našem primeru, kjer smo število 318 delili s številom 5, smo torej dobili količnik 63 ter ostanek 3. Z drugimi besedami, v število 318 lahko "stlačimo" 63 petic, pa še ostane prostor za tri "vitke" enice. 😉 Naloga Izračunaj, koliko je 721 : 4. V tabeli je že označen "namig": Rešitev:
V našem primeru je druga vrstica nekoliko drugačna od tistega, kar se običajno uči v šolah (iz prve vrstice bi se namreč v drugo vrstico poleg ostanka 3 "morala po pravilih" prenesti le dvojka, ne pa celoten preostanek deljenca).
Pravilo sem nekoliko priredil, ker menim, da se učenci postopek lažje zapomnijo, če si predstavljajo, da preostanek števila, ki ni podčrtan, "pade v spodnje nadstropje" :) Kljub "mini spremembi" račun ni napačen, le potrebno je paziti, da v vsaki vrstici podčrtamo nov "vmesni deljenec", kar v "originalnem" postopku ni potrebno. Mogoče nekoliko razmišljanja več, a koraki so s tem poenoteni, kar pa tudi prispeva k lažji razumljivosti. Pazljivost je potrebna edinole v primerih, kjer pri deljenju vmesnega deljenca ni ostanka. Če v koraku, ki sledi, podčrtamo dve števki, je v rezultat potrebno "vriniti" še eno ničlo. Primer: 18300 : 6.
0 Comments
Vemo, da je število deljivo z 2, če se konča z 2, 4, 6, 8 ali 0 ter deljivo s 5, če se konča z 0 ali 5.
Potem pa so tu »naloge z zvezdico«, kjer se naučimo še, da je število deljivo s 4, če sta s 4 deljivi zadnji dve števki oziroma deljivo s 25, če sta s 25 deljivi zadnji dve števki. V primeru, da sta zadnji dve števki enaki 0, je število deljivo tako s 4 kot s 25. Največji ljubitelji matematike se potem naučijo še to, da je število deljivo z 8, če so z 8 deljive zadnje tri števke. Prepoznate vzorec? Pri deljivosti s katerim številom si še lahko pomagamo z zadnjimi tremi števkami? Vrnimo se k deljivosti z 2 in 5. Če pravilo zapišemo podobno kot pravilo za deljivost s 4 in 25, se glasi: Število deljivo z 2, če je z 2 deljiva zadnja števka oziroma deljivo s 5, če je zadnja števka deljiva s 5. Pozabiti pa seveda ne smemo na primer, ko je enica enaka 0. V tem primeru je število deljivo tako z 2 kot s 5. Po tej analogiji bi moralo obstajati še eno število, pri deljivosti s katerim si lahko pomagamo z zadnjimi tremi števkami. Kako ga lahko ugotovimo? Zopet se vrnimo k deljivosti z 2 in 5. Če štejemo naprej po večkratnikih števila 2, se vsak vzorec konča z 0 na mestu enic. Enako velja za štetje po večkratnikih števila 5. Zato je dovolj za deljivost gledati le zadnjo števko. Če štejemo po večkratnikih števila 4, pa se vsak vzorec konča z »00« na mestu desetic in enic. Enako velja za večkratnike števila 25. Zato moramo za deljivost gledati zadnji dve števki. Enako velja za večkratnike števila 8. Tu se vsak vzorec konča z »000« na zadnjih treh mestih. Vse lepo in prav, a še vedno ne vemo, pri deljivosti s katerim številom si še lahko pomagamo z zadnjimi tremi števkami. Pomislimo, kakšna povezava obstaja med 2, 5 in 0 na mestu enic. Kaj pa med 4, 25 in »00« na mestu desetice in enice? 2 ∙ 5 je 10, 4 ∙ 25 pa je 100. 4 ∙ 25 lahko zapišemo tudi kot 2² ∙ 5² oziroma (2 ∙ 5)². Naš odgovor je že skoraj na dlani. Koliko krat 8 je 1000? Oziroma koliko na tretjo potenco krat 2³ je 1000? Po dosedanji logiki 5 na tretjo potenco oziroma 125. Res je, 125 ∙ 8 = (5 ∙ 2)³ = 1000 in število je deljivo s 125, so s 125 deljive zadnje tri števke. Ne verjamete? Poizkusite s kalkulatorjem in enim zelo velikim številom, recimo 45653454243443375:125. Ni važno, kako veliko je število, pomembne so samo zadnje tri števke. Za konec pa še vprašanje. Deljivost s katerimi števili lahko še raziščemo na podlagi ugotovljenega? Kaj ima seštevanje in odštevanje v okviru celih števil skupnega s košarko?
Predstavljajmo si tekmo med plusi in minusi in ves čas spremljajmo razliko v rezultatu:
3 -2 -2 +1 -3 +2 Kakšen je torej trenutni rezultat?
Tudi rezultat računa 3 -2 -2 +1 -3 +2 je enak -1. Minus 1, ker "minusi vodijo za 1 točko". Ko imamo opravka s pozitivnimi števili, ponavadi ni težav, saj »smo z njimi gor rasli«. Pri negativnih številih pa si s »klasičnimi« modeli ne moremo več pomagati (predstavljajte si, da je na avtobusu 5 ljudi, nato pa jih 7 izstopi – mission impossible), zato si je potrebno izmisliti nove. Najdete jih na koncu tega članka, prej pa si odgovorimo še na nekaj vprašanj. Predznak ali računska operacija? Kadar množimo ali delimo, ni dileme: če se vmes pojavi kakšen plus ali minus, gre definitivno za predznak. Pri seštevanju in odštevanju pa zadeva postane že bolj zanimiva, a povsem obvladljiva, če upoštevamo naslednje:
Za predznak je logično, da je negativen, saj pozitivnega ni potrebno pisati, v nalogah pa je potrebna pazljivost, saj nikjer ne piše, da pozitivnega predznaka ne smemo pisati, zato nas učitelji radi presenetijo tudi s kakšnim zapisom v stilu »2+(+3)-(+5) ...« Zakaj moramo predznak postaviti v oklepaj? Zato, ker se z računsko operacijo »ne marata« in ju je potrebno fizično ločiti. :) Ne vem, če je to sicer res, si je pa lahko zapomniti. :) Povrhu zapis brez oklepaja še »grdo zgleda«, recimo 5 - - 3, 6 + - 2 ... Prišteti ali odšteti, to je sedaj vprašanje Ko se pred nami pojavi račun s samimi plusi in minusi, med katerimi je nekaj računskih operacij, nekaj pa predznakov, ga je potrebno najprej poenostaviti, kar marsikomu povzroča težave. Zato sem za vas pripravil nekaj modelov, s katerimi si lahko pomagate. Če si predstavljamo, da računski operaciji seštevanja in odštevanja pomenita segrevanje in ohlajanje, predznak minus pa zanikanje trditve in zamižimo na eno oko glede slovnice, rezultat dobimo že z nekaj logike: Na podoben način si seštevanje in odštevanje lahko predstavljamo kot hojo naprej in nazaj po sobi, pri čemer nas negativni predznak obrne za 180 stopinj: Lahko pa rečemo, da je število s predznakom minus »negativno razpoloženo« in računski operaciji, ki stoji pred njim, »meša štrene« in sicer tako, da plus spremeni v minus, minus pa v plus. :)
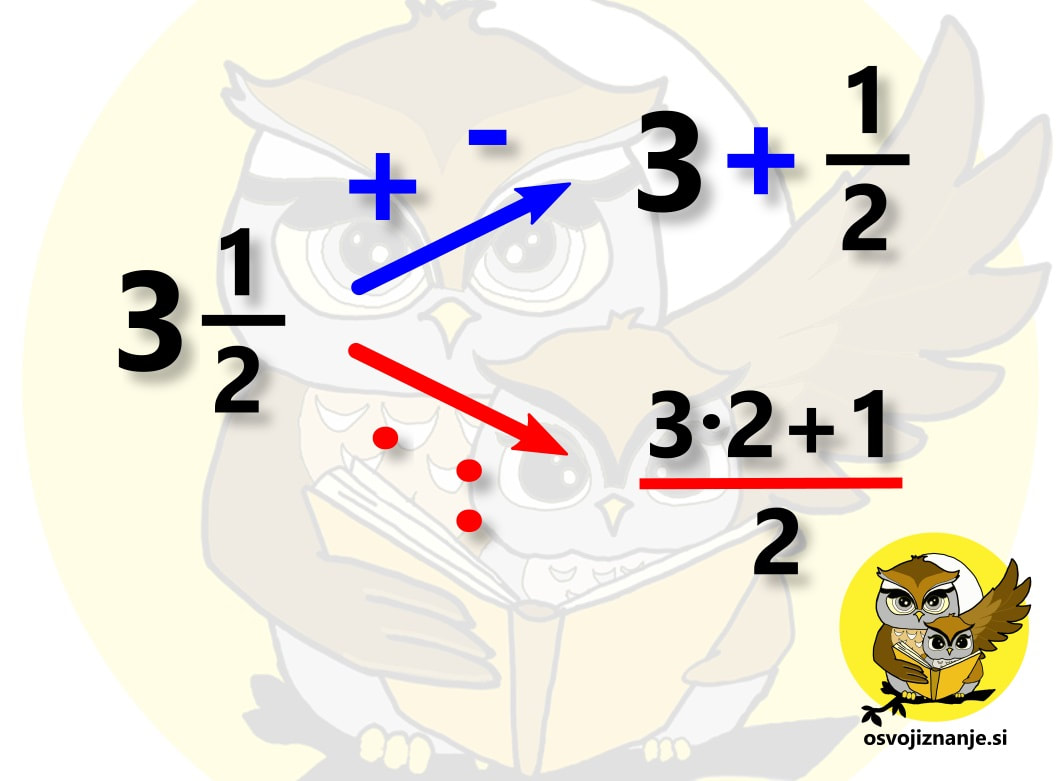
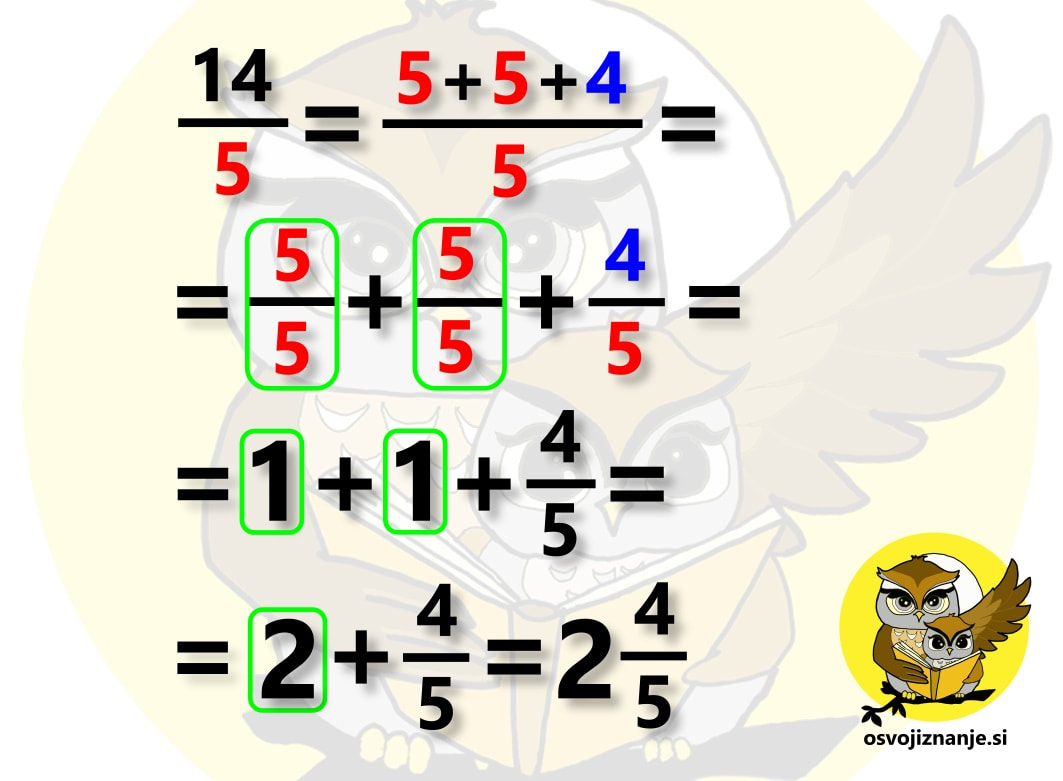
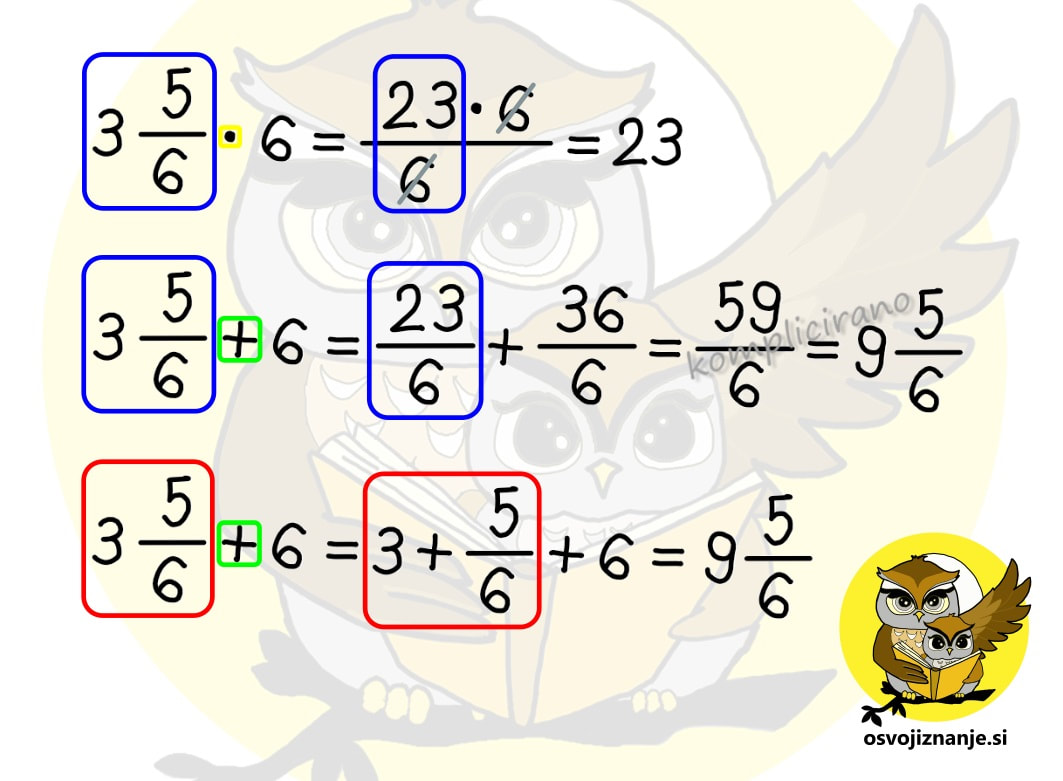
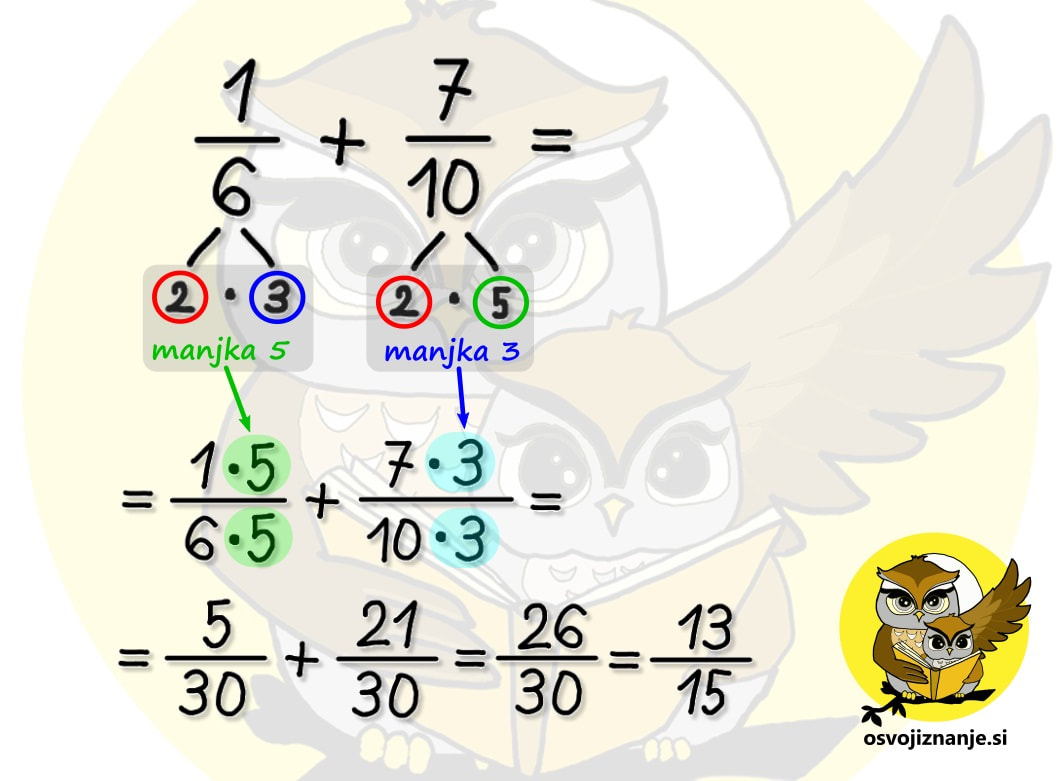
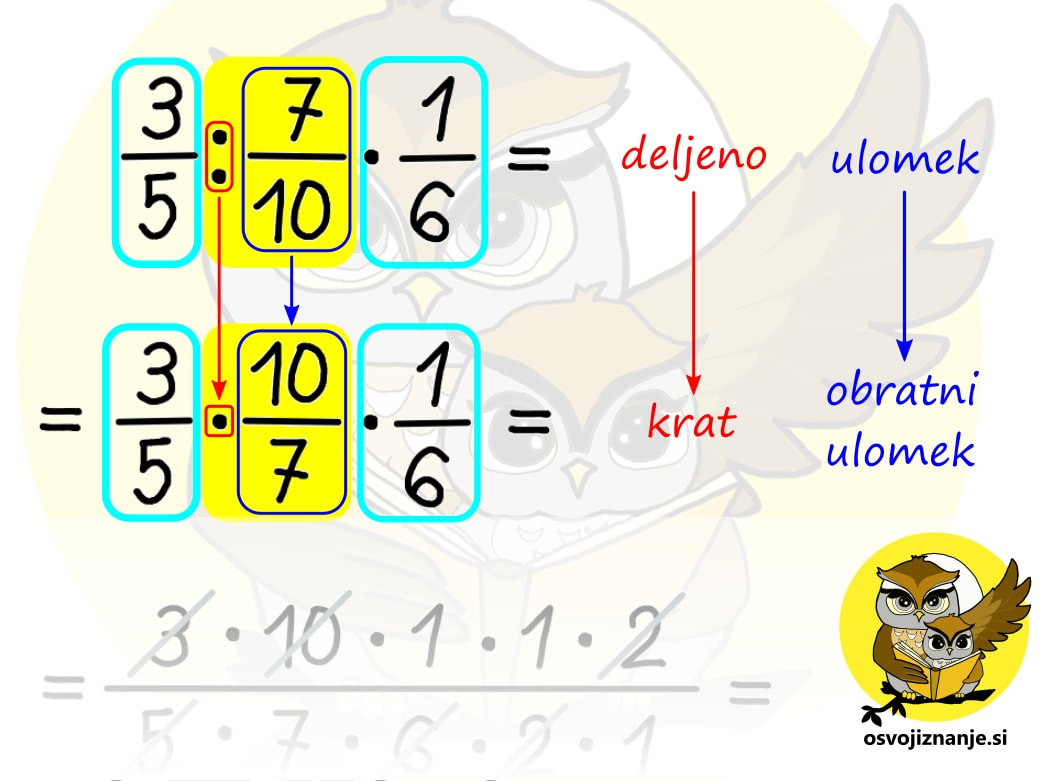
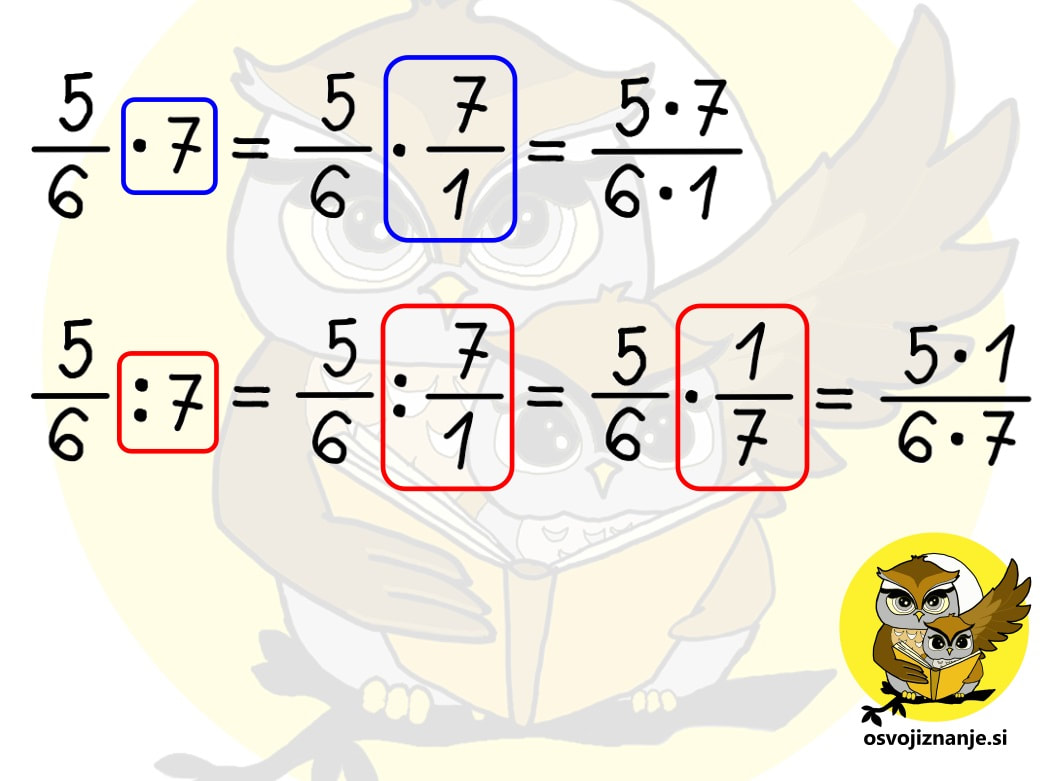
Sedmi razred je pri matematiki za marsikoga kar zalogaj. Praštevila, nato pa ulomki in vse kar pride zraven – krajšanje, razširjanje, primerjanje, iskanje skupnega imenovalca ... in seveda računanje z ulomki. Najprej osnovne računske operacije (seštevanje, odštevanje, množenje in deljenje), nato pa kombinacije le-teh. Da je zadeva še bolj zanimiva, se ulomkom pridružijo še cela, mešana in decimalna števila. Pri obravnavi snovi se seveda vedno mudi in kdor je v nižjih razredih »prešprical« kakšno snov ali pa jo zgolj pozabil (vsi smo ljudje), se hitro znajde v težavah. Da v takih primerih ne bi bilo potrebno takoj klicati inštruktorja, sem pripravil nekaj hitrih nasvetov za »spopad z ulomki«. :) Kako obravnavati mešano število? Mešano število je število, ki je sestavljeno iz celega števila in ulomka, na primer 3 in ena polovica (glej sliko). Marsikdo ob pogledu na tako število začne v imenovalcu takoj množiti 3 z 2 in prištevati 1 ... (spodnji ulomek na desni strani slike). To je seveda pravilen postopek, a ga ni »modro« uporabljati v vseh primerih, ampak le pri množenju in deljenju. Pri seštevanju in odštevanju pa je mešani ulomek lažje zapisati »na dolgo« in sicer v obliki celo število + ulomek (zgornji ulomek na desni strani slike). Zakaj »na dolgo«? Zato, ker je zapis mešanega števila v bistvu skrajšan zapis vsote celega števila in ulomka. Kako odšteti ulomek od celega števila? V takem primeru lahko uporabimo t.i. »strategijo izposojanja«. V našem primeru na spodnji sliki si od 3 »izposodimo« 1, ki jo nato zapišemo v obliki ulomka. Število 1 v obliki ulomka zapišemo tako, da izenačimo vrednost števca in imenovalca, ta pa je lahko karšna koli celoštevilska vrednost. Ker v našem računu nastopa še en ulomek, ki ima vrednost imenovalca 7, enako vrednost uporabimo tudi pri ulomku, ki predstavlja celoto, saj nam tako ni potrebno iskati skupnega imenovalca. Enako strategijo lahko uporabimo tudi pri odštevanju ulomka od mešanega števila, če je ulomek, ki ga odštevamo, večji od ulomka zraven celega števila (npr. 5 2/5 – 3/5). Kako odšteti mešani ulomek? Za mešani ulomek vemo, da je skrajšan zapis vsote celega števila in ulomka. Če tak ulomek prištevamo, lahko enostavno zapišemo celo število + ulomek. Če pa ga odštevamo, ne smemo pozabiti, da minus pred njim »zagrabi« tako na celo število kot na ulomek (podobno kot če bi imeli oklepaj), zato je potrebno odšteti tako celo število kot ulomek. Kdaj je priporočljivo »nepravi ulomek« spremeniti v mešano število in kako to storim? Če ima ulomek »zgoraj več kot spodaj« oziroma ima števec večji od imenovalca, zanj rečemo, da je nepravi. Tak ulomek je »vreden« več kot 1, zato »lepše«, če ga zapišemo kot vsoto celega števila in ulomka oziroma »tistega, kar ostane«. Vemo, da ulomke seštevamo tako, da števce seštejemo, imenovalec pa prepišemo. Kaj pa, če bi to pravilo uporabili »v rikverc«? Števec ulomka lahko zapišemo kot vsoto vrednosti v imenovalcu in ji prištejemo »tisto, kar ostane«. V našem primeru števec 14 zapišemo kot vsoto dveh petic in »preostale« štirice (5+5+4). Tak ulomek lahko razdelimo na 3 ulomke (5/5, 5/5 in 4/5), od katerih sta prva dva enaka 1, zato ju lahko zapišemo kot celoštevilsko vrednost 2, zadnji ulomek (4/5) pa dopišemo zraven. Kdaj moram mešano število spremeniti v »nepravi ulomek« in kako to storim? Takrat, kadar mešano število množimo ali delimo s celimi števili ali ulomki. Primer množenja mešanega števila s celim številom je prikazan v prvi vrstici spodnje slike. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Druga in tretja vrstica spodnje slike predstavljata isti račun (seštevanje mešanega števila s celim številom), rešen na dva načina. V drugi vrstici vidimo, da smo iz povsem enostavnega seštevanja znotraj desetice prišli na račun 23+36, katerega rezultat je potrebno potem deliti še s 6, da dobimo celi in ulomljeni del rešitve. V tretji vrstici pa enostavno seštejemo celi števili, prištejemo ulomljeni del in brez pretiranega napora dobimo, seveda, enak rezultat. :) Kako najlažje poiščem (najmanjši) skupni imenovalec? Pred časom sem na inštrukcijah poskusil z metodo »nogic« oziroma »rožičkov«, ki se jo mogoče kdo spomni še iz nižjih razredov osnovne šole. Za razliko vrednosti na krajiščih »nogic« tu ne seštevamo ampak množimo, pred tem pa število razcepimo na prafaktorje. Ker to počnemo grafično, zadeva utegne postati celo zabavna. ;) Več o sami metodi si lahko preberete v članku o računanju s pomočjo številskih dreves. V čem je »trik«? Vzemimo za primer račun s spodnje slike. Prvi seštevanec ima imenovalec enak 6, drugi pa 10. Po razcepu na praštevila na »nogice« prvega imenovalca zapišemo 2 in 3 (2 · 3 = 6), na nogice drugega pa 2 in 5 (2 · 5 = 10). »Fora« najmanjšega skupnega imenovalca je v tem, da s »čim manj potezami« imenovalca izenačimo. Pri tem seveda lahko uporabimo zgolj računsko operacijo množenja, množiti (z istim številom!) pa moramo tako »spodaj« (imenovalec) kot »zgoraj« (števec), sicer vrednost ulomka spremenimo, kar pa ni okej. Poglejmo, kako lahko imenovalca izenačimo v našem primeru. Prvi ulomek »ima« 2 in 3, drugi pa 2 in 5. Z »najmanj potezami« imenovalca izenačimo tako, da na prvi imenovalec dodamo (števec in imenovalec množimo s) 5, na drugega pa 3. Tako sta oba imenovalca enaka 2 · 3 · 5 = 30, števca pa sta po množenju enaka 5 oziroma 21. Ulomka nato še seštejemo in okrajšamo oziroma poenostavimo in dobimo rezultat trinajst petnajstin. Če imamo večja števila, imenovalce lako »drobimo« postopoma (drevo se bolj razveji), upoštevamo pa zgolj številke na končnih vej(ic)ah. Te za boljšo vidnost lahko tudi obkrožimo. Ko smo že nekoliko bolj izkušeni, nam imenovalcev ni potrebno drobiti povsem do praštevil. Če imamo na primer imenovalca enaka 8 in 12, lahko zapišemo 8 kot 2 · 4, 12 pa kot 3 · 4. 4 nam ni potrebno drobiti naprej na 2 · 2, saj se 4 nahaja v obeh imenovalcih s takim »kompliciranjem« ne bi nič pridobili, le hitreje bi se lahko zmotili. :) To je seveda zgolj eden izmed možnih načinov. Če v njem nekako »ne najdete«, pa lahko »pokukate« še tale članek. Kdaj moram »obrniti ulomek«? Računanju z obračanjem ulomka »uradno« rečemo množenje z obratno vrednostjo ulomka. Ker je deljenje z ulomkom »smotano« :) (pojavijo se dvojni ulomki in druge neprijetnosti), raje uberemo drugo pot, pri čemer modro izkoristimo naslednja dejstva:
Iz tega sledi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Obratno vrednost ulomka določimo zelo enostavno, saj zgolj zamenjamo vrednosti števca in imenovalca (ulomek obrnemo »na glavo«). :) Kdaj moramo torej »obrniti ulomek«? Vsakič, kadar računsko operacijo deljenja zamenjamo z množenjem. In zakaj to počnemo? Zato, ker je množenje z ulomkom enostavnejše od deljenja. A ne pozabimo: obrnemo vedno zgolj tisti ulomek, ki stoji desno od znaka za deljenje (ki postane znak za množenje)! Še nekaj za »nerde«. Če potegnemo analogijo s seštevanjem in odštevanjem, lahko zapišemo ...
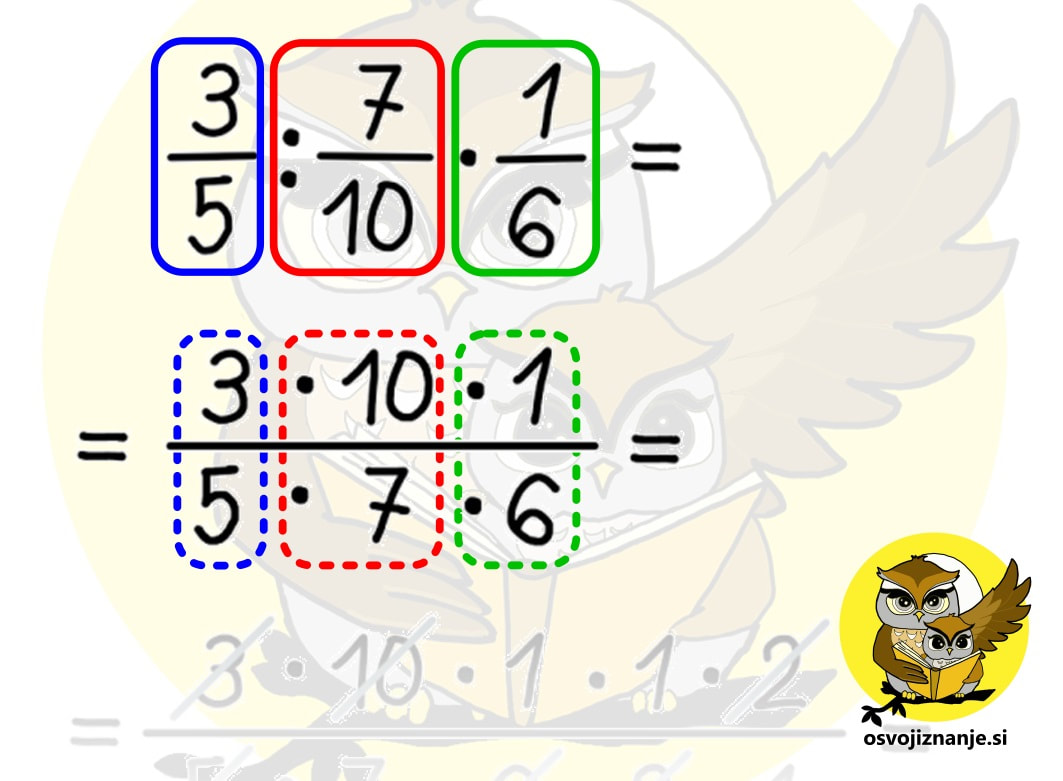
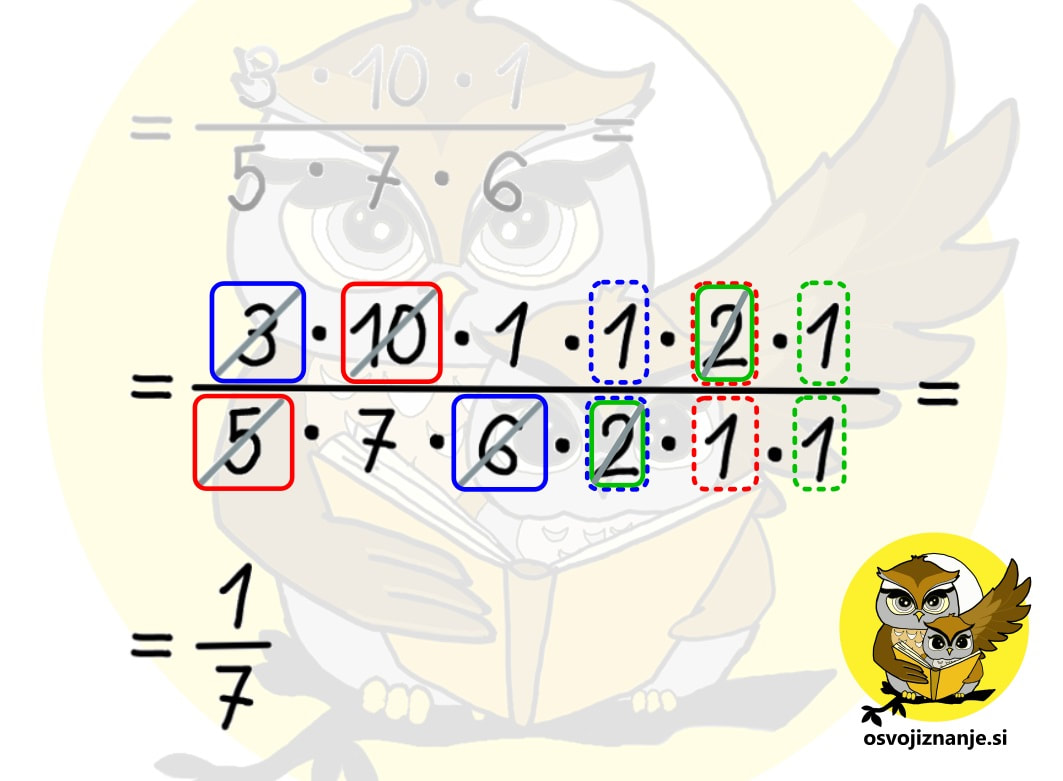
Za konec pa še nekaj za »toplt nerde« :) Vemo, da velja enakost a-(-a) = a+a. Po analogiji bi lahko zapisali tudi a:(:a) = a·a, ampak bi nas kak matematik »za ušesa«. :) Omenjeni zapis namreč ni dovoljen, saj »:« v prvem oklepaju ni predznak, tako kot »-« v drugem oklepaju. Lahko pa drugi zapis popravimo v a:(1:a) = a·a oziroma v a:(1/a) = a·a. Pa smo spet pri naši ugotovitvi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Pa še nekaj. Predznaka »+« nikoli ne pišemo, čeprav »vemo, da je tam«. Zato tudi prvi člen na skrajni levi strani računa v primeru, da je pozitiven, nima predznaka. Po drugi strani moramo predznak »-« vedno zapisati. Kadar imamo opravka hkrati s predznakom »+« ali »-« in računsko operacijo »+« ali »-«, velja pravilo, da dva »-« dasta »+« (o, ko bi bilo tako tudi pri ocenjevanju!) :) Predznaka »krat« in »deljeno« pa kot taka ne obstajata, zato se nikoli ne bomo srečali npr. z računom 10:(:5), bomo pa srečali račun npr. 10:(1/5), ki se od prvega praktično ne razlikuje, saj enica pri množenju in deljenju ne spremeni vrednosti računa. In tu se lahko spomnimo pravila »dva minusa dasta plus«, saj analogno tudi »dve deljenji dasta množenje« (matematiki bi nas spet za ušesa :)) in račun 10:(:5) oziroma 10:(1/5) postane 10 · 5. To si velja zapomniti, saj nas analogija pogosto lahko reši iz zadrege, če kaj pozabimo. A pozor – učitelju ne skušajte »prodati« računa 10:(:5), ampak vmes vrinite tisto enico (10:(1/5)), da vas – ne bo za ušesa seveda. :) Več na temo povezav med seštevanjem in odštevanjem oz. med množenjem in deljenjem ter nasprotnih in obratnih vrednostih pa najdete v samostojnem članku. Kdaj lahko »dam vse na eno dolgo ulomkovo črto«? Kadar imamo v računu (ali v delu računa) samo množenje in deljenje ulomkov ter celih števil, lahko vse skupaj zapišemo na eno ulomkovo črto, ki jo po potrebi podaljšamo (če je možno kaj »krajšati« oziroma, bolj pravilno rečeno, poenostaviti). Pri zapisu na »dolgo« ulomkovo črto ulomkov, pred katerimi stoji znak za deljenje, ne pozabimo »obrniti okoli«. Deljenje se v tem primeru spremeni v množenje, tako da ima taka »dolga« ulomkova črta tako v števcu kot v imenovalcu zgolj računsko operacijo množenja, kar nam omogoča enostavno krajšanje. Ali lahko ulomke lahko krajšam »križkraž«? Seveda. In to večkrat. :) Zakaj? Ker imamo tako v imenovalcu kot v števcu račun, ki vsebuje zgolj množenje, za katerega velja zakon o zamenjavi (recimo 3 krat 5 je isto kot 5 krat tri ...) Na spodnji sliki vidimo, da 3 v števcu in 6 v imenovalcu lahko krajšamo s 3, 10 v števcu in 5 v imenovalcu pa z 2, kljub temu, da ne ležijo »eden pod drugim«. 2 v imenovalcu iz prvega krajšanja in 2 v števcu iz drugega krajšanja lahko nato še enkrat krajšamo z 2. Aja, pa še nekaj. Lepše kot »krajšati« se sliši »poenostaviti«, saj po tem postopku ulomek ni nič »krajši«, J ampak zgolj poenostavljen, saj je vrednost okrajšanega ulomka enaka »originalnemu« ulomku. Kdaj je priporočljivo celo število pretvoriti v ulomek in kako to storim? Kadar celo število nastopa "v družbi ulomkov" v računu množenja ali deljenja, ga je najbolj enostavno pretvoriti v ulomek in nato z njim računati tako kot z ulomkom. Na ta način se ne bomo nikoli spraševali, ali ga je potrebno zapisati v števec ali imenovalec ulomka. Celo število v ulomek pretvorimo tako, da ga zapišemo v števec (zgoraj), v imenovalec (spodaj) pa zapišemo vrednost 1. Dokaj logično, če vemo, da ulomek predstavlja deljenje, deljenje z 1 pa na deljenca nima vpliva. Primer: 5=5/1. Če s tem številom množimo, vemo, da gre 5 v števec "dolge ulomkove črte", 1 pa v imenovalec. Če pa z njim delimo, vemo, da ga moramo "obrniti na glavo", zato na "dolgo ulomkovo črto" zapišemo 1 zgoraj, 5 pa spodaj. Če imamo poleg celega števila zraven še ulomek, je tak zapis pri množenju in deljenju potrebno pretvoriti v »nepravi ulomek«. Za več »poskrolajte« malo višje po članku. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Če »gremo kje čez«, nepravi ulomek pretvorimo v pravega, celoštevilski del pa ustrezno povečamo. Če »nam kje zmanjka«, pa si od celega števila »izposodimo« ulomek tipa n/n in odštevanje izvedemo posebej za cela števila in posebej ulomke. Za podrobnejšo razlago »poskrolajte« malo višje po članku. Kdaj je koristno decimalno število pretvoriti v ulomek?
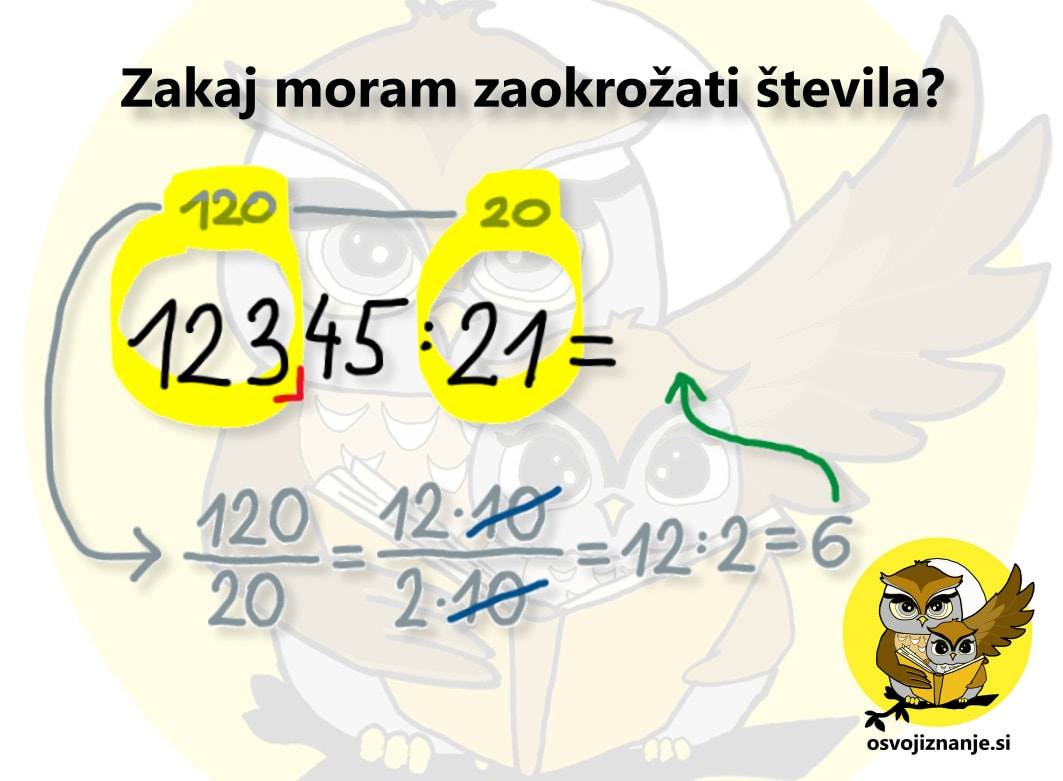
Marsikdo »ne mara ulomkov«, zato v računih, kjer nastopa kombinacija decimalnih števil in ulomkov, slednje vedno pretvori v decimalna števila in se potem »igra s premetavanjem decimalnih vejic«. Poleg tega, da je tako računanje »manj elegantno«, rezultat take pretvorbe ni vedno končno decimalno število, zato ga moramo zaokrožiti, s čimer pa »pridelamo« tudi nekaj pogreška. Zakaj je računanje s pretvorbo ulomkov v decimalna števila »manj elegantno«? Naloge so velikokrat zastavljene tako, da je pri računanju z ulomki »manj pisanja« in veliko faktorjev se »lepo krajša«, tako da tak račun izgleda »lepše« oziroma bolj pregledno. Po drugi strani se pri računanju z decimalnimi števili ni potrebno ukvarjati s pravili za računanje z ulomki, a moramo biti zelo pozorni na decimalne vejice. V računih, kjer nastopa kombinacija decimalnih števil in ulomkov, je decimalno število koristno pretvoriti v ulomek predvsem pri množenju in deljenju z ulomki, medtem ko je pri seštevanju in odštevanju včasih lažje, če naredimo obratno – ulomek pretvorimo v decimalno število, predvsem takrat, kadar je rezultat take pretvorbe končno decimalno število. Ker pisno deljenje velja za postopek, v knjigah in na spletu mrgoli "kuharskih receptov" z vrstnim redom opravil, ki ga je potrebno dosledno upoštevati, če ne želimo npr. bankrotirati, ko bomo 100 evrov med 10 sodelavcev razdelili tako, da bomo vsakemu dali 1000 evrov. ;) Tako kot življenje pa ne poteka vedno "po ravni črti", se tudi pri pisnem deljenju včasih kje ustavi. In če znamo zgolj postopek na pamet, je račun potrebno prečrtati in začeti znova. "Tekoče znanje matematike" namreč ne pomeni, da znamo vse postopke na pamet, ampak je to sposobnost, da se "izmotamo iz težav", ko naletimo nanje. Recimo, da pozabimo korak postopka ali pa se pri prejšnjem koraku zmotimo. Takrat nam po glavi začnejo rojiti različna vprašanja in zaželimo si, da bi imeli ob sebi nekoga, ki bi ga lahko prosili za pomoč. S tem namenom sem tokratni članek oblikoval v obliki vprašanj in odgovorov. Upam, da vam bo v pomoč. :) Koliko števk deljenca (na levi) moram vzeti za prvi izračun? Ravno prav. :) Pojdimo lepo po vrsti, pri tem pa si pomagajmo s primerom na sliki. Kot vemo, je deljenje enako ulomku in ulomek s števcem, manjšim od imenovalca, je manjši od 1. V okviru celih števil je to 0 (v minus ne gremo). Če bi torej vzeli premalo števk (v našem primeru le prvo ali prvi dve), bi bil rezultat deljenja manjši od 1 in prva števka količnika (desno od enačaja) bi bila 0. S tem sicer ni nič narobe, a je brez smisla, saj ničel pred števili ne pišemo. Tudi preveč števk (npr. prve štiri) ne bi bila dobra rešitev, saj bi bilo računanje preveč zahtevno, s čimer bi algoritem izgubil smisel. V našem primeru je torej najbolje izbrati tri števke, s čimer je celoštevilski rezultat prvega deljenja enomestna vrednost (1, 2, 3 ... ali 9), v našem primeru 6. Ta vrednost je hkrati tudi prva števka rezultata (količnika) in jo bomo bomo zapisali desno od enačaja, kar bo razvidno v nadaljevanju. Zakaj moram zaokrožati števila? Zato, ker večmestna števila delimo lažje, če so le-ta večkratniki potenc števila 10 (imajo na desni strani eno oziroma več ničel). Ker deljenje predstavlja ulomek, lahko posamezno število zapišemo kot zmnožek nekega števila in potence števila 10, nakar te potence enostavno okrajšamo. V primeru na sliki deljenec 123 zaokrožimo na 120, delitelj 21 pa na 20. Ker velja 120 = 12 · 10 in 20 = 2 · 10, lahko 10 enostavno okrajšamo in dobimo nov račun 12 : 2, za kar pa vemo, da je enako 6. Zakaj moram pri računu deljenja množiti? Algoritem je zasnovan tako, da lahko računamo s približki in oceno (po domače povedano »na palec«), kar nam sicer olajša delo, a za točen rezultat moramo pri vsakem koraku narediti preverjanje, za koliko smo pri ocenjevanju rezultata zmotili oziroma, po domače, »udarili mimo«. :) Pogrešek pri deljenju preverimo z množenjem, ker pa množenje velja za nasprotno računsko operacijo od deljenja, ju izvedemo v nasprotnih smereh. Enostavno si lahko zapomnite, da »delimo v smeri računanja (z leve), množimo pa z nasprotne smeri (z desne)«. V našem primeru smo za račun deljenja uporabili »števili z leve« (123 in 21 oziroma njuna približka 120 in 20), za račun množenja pa »števili z desne« (21 in 6). 120 : 20 oziroma 12 : 2 nam da količnik 6. Z množenjem delitelja (21) in tega količnika (obarvana rožnato) preverimo, če je bila naša ocena pravilna. 21 · 6 = 126, kar je več od 123, torej smo se pri ocenjevanju zmotili. Kaj pa sedaj? Odgovor na to najdete v nadaljevanju, na tem mestu zgolj razlaga, zakaj to presneto množenje. ;) Kako vem, da je števka količnika, ki sem jo zapisal v posameznem koraku deljenja, pravilna? Rezultat »množenja nazaj« v posameznem koraku vedno primerjamo s »trenutnim« deljencem. Pozor! To ni celotni deljenec, ampak le določene števke le-tega (na sliki so označene z modro barvo):
V našem primeru smo najprej »naračunali« preveč (21 · 6 je enako 126, kar je več od 123, označeno z modro), zato smo števko količnika morali zmanjšati za 1 (iz 6 na 5) in še enkrat izračunati račun množenja. Zmnožek 21 · 5 je enak 105, kar je manj od »trenutnega deljenca« (123), razlika med 123 in 105, ki je enaka 18, pa je tudi manjša od delitelja (21), zato je števka količnika v tem koraku pravilna, torej 5. Kako najlažje pridem do vrednosti, ki jo je potrebno podpisati na levi strani? Že v prejšnjem poglavju smo ugotovili, da je razlika med zmnožkom »množenja nazaj« (105) in »trenutnega« deljenca (123) enaka 18, nismo pa povedali, kako do te razlike najlažje pridemo. Na sliki je prikazana strategija s približevanjem preko »okroglih« števil (angl. under strategy). Za okrogla števila štejemo večkratnike potenc števila 10, v angleškem jeziku zanje pogosto slišimo izraz »friendly numbers«. Namesto te strategije bi lahko uporabili tudi strategijo s prištevanjem »okroglega« števila in vračanjem nazaj (angl. over strategy): 123 + 20 - 2. Omenjen način je marsikomu mogoče nekoliko neobičajen, saj je navajen »klasičnega« računa odštevanja v stolpcu (123 - 105), ampak omogoča veliko boljši vpogled v sam koncept pisnega deljenja. Saj se tudi vprašamo ponavadi: »Koliko od 105 manjka do 123?« in ne: »Koliko je 123 minus 105?« :) Kako pravilno podpisujem? Pri podpisovanju si zapomnite predvsem to, da enico podpisanega števila zapišete točno pod enico »trenutnega deljenca«. V našem primeru to pomeni 8 (enica števila 18) pod 3 (enica števila 123). Za lepši in bolj sistematičen izgled je seveda dobro zapisati tudi desetice pod desetice, stotice pod stotice itd., a za opisani način reševanja s pomočjo številskega traka to ni bistveno. Pri prvem podpisovanju si lahko pomagamo tudi s »kaveljcem«, ki označuje konec »trenutnega deljenca« (v našem primeru stoji med števkama 3 in 4 deljenca), pri podpisovanjih, ki sledijo, pa pazimo na to, da gremo v vsakem koraku za eno mesto v desno. Zakaj pa moramo paziti na to, da so enice pod enicami? Zato, ker bomo naslednjem koraku na desno stran podpisanega števila dodali naslednjo števko deljenca (v našem primeru je to števka 4), s čimer bomo dobili nov »trenutni deljenec«. In če je podpisana vrednost zamaknjena v levo ali v desno, se nam lahko zgodi, da bomo na desni strani dopisali napačno števko (v našem primeru 3 ali 5), kar za naš račun ne pomeni nič dobrega. Več o tem povem v naslednjem poglavju o »padajočih števkah«. :) Kaj pri pisnem deljenju »pada dol«? Podpisovanju razlike med zmnožkom »množenja nazaj« in »trenutnega deljenca« vedno sledi dodajanje naslednje števke deljenca na desno stran te razlike, s čimer dobimo »trenutni deljenec« za naslednji korak deljenja. Ste kaj razumeli? Brez skrbi, z razlago ob primeru bo lažje. ;) V našem primeru je razlika med zmnožkom »množenja nazaj« (21 · 5 = 105) in »trenutnega deljenca« (123, na rumenem polju do rdečega »hakeljca«) enaka 18. Kot je bilo rečeno že prejšnjem poglavju, pazimo, da je enica te razlike (8) točno pod enico trenutnega deljenca (3). Po domače rečeno »se držimo desnega robu rumenega polja«. Celotni deljenec je v našem primeru enak 12345, »trenutni deljenec« (v prvem koraku) pa predstavljajo njegove prve tri števke (123, v rumenem polju do »hakeljca«). Naslednja števka deljenca je tako (v prvem koraku) 4, ki prva sledi »hakeljcu«. Za lažjo predstavo ta števka leži na modri podlagi. To števko (4) nato dodamo na desno stran razlike (18), po domače lahko rečemo, da 4 »pade dol«. Za lažjo predstavo je pot padanja obarvana modro. Ko 18 in 4 »sestavimo skupaj«, dobimo »trenutni deljenec« za naslednji korak, to je 184. Tega nato delimo z 21 in tako naprej ... Kdaj je podpisovanja konec? Predpostavimo, da želimo rezultat zapisati v obliki celoštevilskega količnika in ostanka. S postopkom, opisanim v prejšnjem koraku, nadaljujemo toliko časa, da »pade dol« še zadnja števka celotnega deljenca, s čimer dobimo naš zadnji »trenutni deljenec«. Deljenje zadnjega »trenutnega deljenca« z deliteljem nam da še zadnjo števko količnika in ostanek. V našem primeru je celotni deljenec enak 12345, torej je njegova »zadnja števka« 5. To zapišemo desno od razlike 16, ki smo jo podpisali pod prejšnji »trenutni deljenec« 184. Naš zadnji »trenutni deljenec« je tako 165. Za količnik 165 : 21 smo ocenili vrednost 7. Ta postane zadnja števka količnika (587). Razlika med zmnožkom »množenja nazaj« (21 · 7 = 147) in »trenutnim deljencem« (165) pa je enaka 18. Ta razlika je naš ostanek, saj – po domače - »nima več kaj dol pasti«. V primeru, da želimo rezultat zapisati v obliki decimalnega števila, za zadnjo zapisano števko delitelja zapišemo decimalno vejico in s postopkom nadaljujemo vse dokler je razlika med zmnožkom »množenja nazaj« in »trenutnim deljencem« različna od nič. To lahko traja tudi »v neskončnost«, zato je včasih potrebno na neki decimalki rezultat zaokrožiti. Več o tem postopku povem kdaj drugič. ;) Kako vem, da je rezultat pravilen (oziroma vsaj smiseln)?
Marsikdo od nas je verjetno že kdaj na testu oddal kakšno »neumnost«, recimo rezultat za premer atoma, merjen v centimetrih. :) V izogib takim spodrsljajem je dobro izračun preveriti oziroma rezultat oceniti »na palec«, bodisi pred zapisom končnega odgovora ali pa že na začetku, da vemo, kaj pričakovati. Pri računu deljenja to lahko storimo zelo enostavno tako, da deljenec zaokrožimo na dve, delitelj pa na eno številsko mesto (več o zaokroževanju si lahko preberete tule), okrajšamo odvečne ničle in izračunamo »kar ostane«. Zakaj zaokrožati na tak način? Zato, ker s tem dobimo preprost račun deljenja dvomestnega števila z enomestnim, katerega lahko enostavno rešimo že s poznavanjem poštevanke in nekaj »premetavanja« ničel. V našem primeru deljenec 12345 zaokrožimo na 12000 (številska mesta štejemo od leve proti desni), delitelj pa na 20. Ker je deljenje isto kot ulomek, zadnji ničli lahko enostavno »okrajšamo« in dobimo račun 1200 : 2, katerega rezultat je 600. Račun deljenja »iz poštevanke«, ki ga moramo pri tem izračunati, je 12 : 2, kar je enako 6, ničli v deljencu pa se »preneseta« na količnik. Računanja pri matematiki marsikdo ne mara, medtem ko je geometrija, vzorci, marsikje tudi logika in kombinatorika med bolj priljubljenimi.
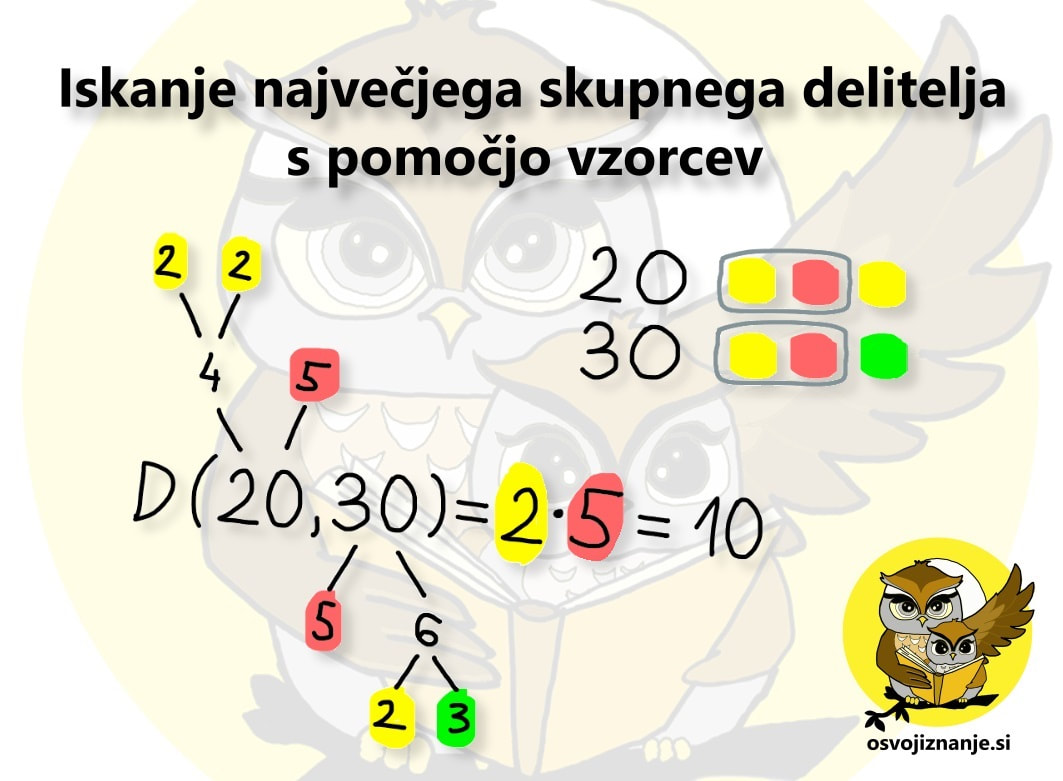
Tudi za določanje največjega skupnega delitelja (z VELIKO črko D ga označimo zato, ker je NAJVEČJI) obstaja "neračunska" metoda in sicer s pomočjo vzorcev. Navodilo je preprosto, oglejmo si ga na primeru iskanja največjega skupnega delitelja števil 20 in 30:
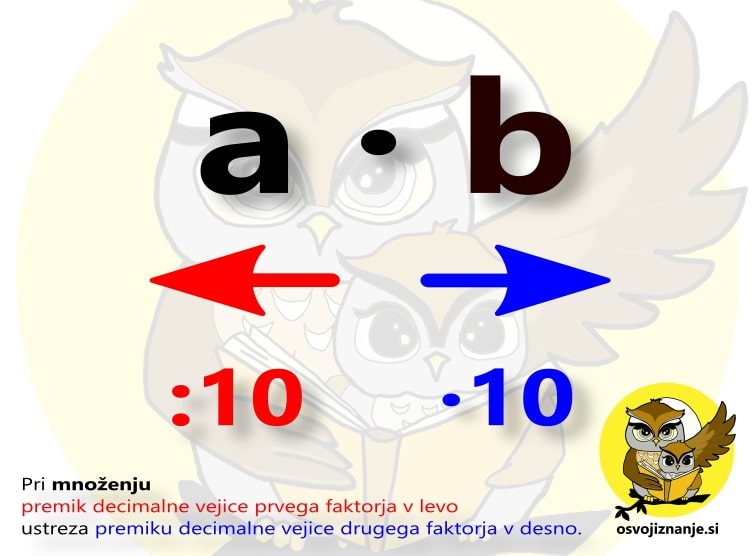
Omenjeno metodo lahko uporabimo tudi za iskanje največjega skupnega delitelja več števil. Množenje Množenje dveh števil, od katerih eno vsebuje decimalno vejico, drugo pa je večkratnik desetiške enote (po domače: konča se z ničlami), si lahko poenostavimo s tem, da decimalna mesta in ničle "kompenziramo". Kompenzacija lahko poteka v eno ... ... ali pa v drugo smer: Matematično ozadje je preprosto. Če neko število (v našem primeru produkt a ∙ b) delimo z 10 (premik decimalne vejice v levo) in nato še množimo z 10 (premik decimalne vejice v desno), dobimo seveda isto število. Predstava bo še lažja s pomočjo primera:
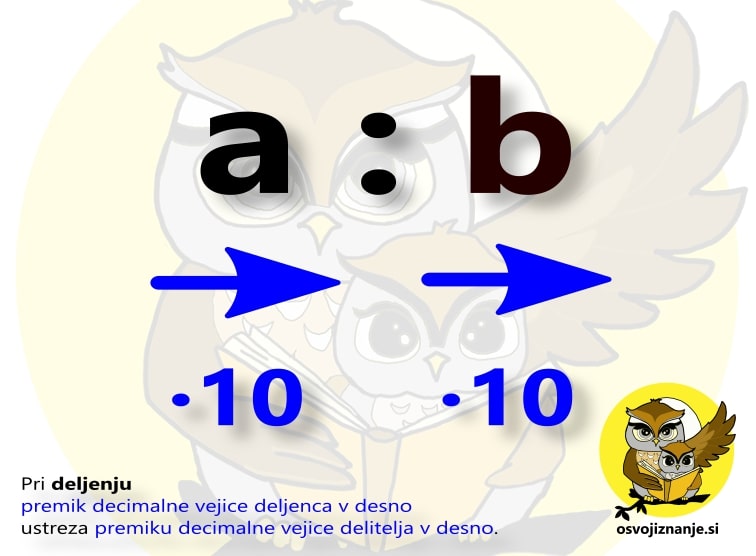
Deljenje Pri deljenju pa se decimalna mesta in ničle za razliko od množenja ne "kompenzirajo" ampak se premik decimalne vejice naredi pri deljencu in delitelju v isto smer. Če deljenec ali/in delitelj vsebuje decimalno vejico, naredimo premik v desno za toliko mest, da sta tako deljenec kot delitelj celi števili: Če ob tem deljencu ali delitelju "zmanjka" decimalnih mest, mu ob vsakem premiku na desno dodamo eno ničlo (več o tem v primerih, ki sledijo). Če pa je deljenec ali/in delitelj večkratnik desetiške enote (po domače: ima na desni strani eno ali več ničel), hkrati odvzamemo obema toliko ničel na desni, da vsaj eden izmed njiju ni več večkratnik desetiške enote (po domače: ima na mestu enic števko, različno od 0): Oglejmo si dva primera. V prvem delimo število 10 z 0,2.
V drugem primeru pa število 600 delimo s 30.
Glede na to, da je ena izmed interpretacij ulomkov razmerje, bi ulomke lahko krajšali in razširjali oziroma pretvarjali na določeni števec ali imenovalec tudi s tabelo razmerij (angl. ratio table). Preden si ogledamo nekaj primerov, najprej razmislek v povezavi z izrazoma krajšanje in razširjanje ulomkov. Pam Harris, predavateljica na Teksaški univerzi, avtorica številnih knjig in promotorka poučevanja t.i. »prave matematike« (angl. »real math«) me je opozorila, da je primernejši izraz za hkratno deljenje števca in imenovalca z istim številom poenostavljanje, saj vrednost ulomka po »krajšanju« ni nič manjša kot prej. Tudi »razširjanje ulomka« bi bilo po tej analogiji bolje imenovati pretvorba ulomka na določeno vrednost števca oz. imenovalca. Primer 1: poenostavi ulomek 180/300:
Števec in imenovalec smo dvakrat razpolovili (deljenje ulomka z 2), nato pa ju delili s 3 in nazadnje s 5. Primer 2: pretvori ulomek na vrednost števca 18:
Števec in imenovalec smo trikrat podvojili (množenje ulomka z 2), nato pa sešteli vrednosti v prvem in četrtem stolpcu s številkami (2+16=18, 3+24=27). Pozor! Tu ne gre za seštevanje ulomkov 2/3 in 16/24! Pomislimo na reševanje sistemov enačb (metoda nasprotnih koeficientov) ... Pri takem sklepanju se osredotočimo na števec, a ne pozabimo na imenovalec! Primer 3: pretvori ulomek na vrednost imenovalca 100:
Števec in imenovalec smo podvojili, nato pa smo ju pomnožili še z 10.
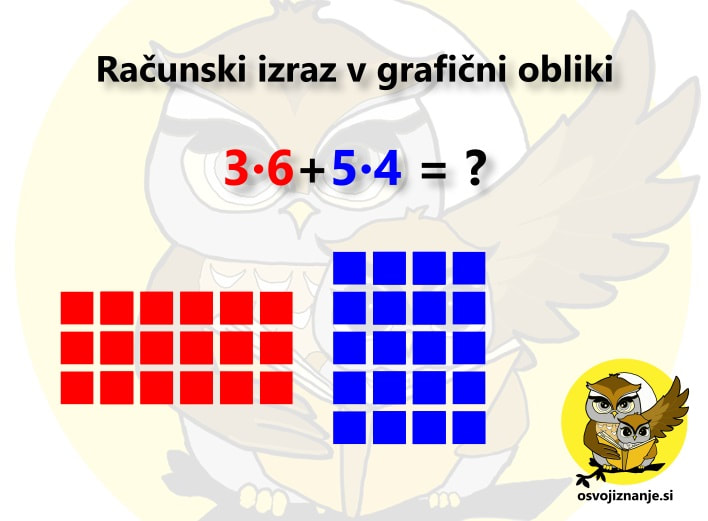
Pri takem sklepanju se osredotočimo na imenovalec, a ne pozabimo na števec! Za konec pa še odgovor na vprašanje: »Zakaj je pretvarjanje ulomkov sploh potrebno?« V tem najdemo vsaj dva smisla. Zakaj poenostavljamo, nam pove že samo ime – zato, da je ulomek enostavneje zapisati, ga prebrati, si ga zapomniti ... Pretvarjanje na določeno vrednost imenovalca, točneje na potence števila 10, pa nam pomaga pri pretvorbi ulomka v decimalno število ali odstotek. Smisla pretvarjanja na določeno vrednost števca pa do danes še nisem našel, čeprav v učbenikih najdemo tudi take naloge. :) Marsikdo si težko zapomni, da ima množenje (in deljenje) prednost pred seštevanjem (in odštevanjem). Predstavljajmo si, da se v testu pojavi račun 3∙6+5∙4. Ker smo itak živčni, pozabimo katera računska operacija ima prednost. Seštevanje ali množenje? Iz zagate nas reši grafični model računa: Če izraz zapišemo (ali pa si ga zgolj predstavljamo) v grafični obliki (v našem primeru 3 vrste po 6 in 4 vrste po 5), vidimo, da vse elemente (npr. kvadratke) preštejemo tako, da najprej izračunamo polji (računa na krat), nato pa vse skupaj še seštejemo.
Za konec pa še izziv za vas. Kako bi grafično predstavili račun 8∙7-6∙5? Kaj pa 9∙5-6∙7? (V prvem primeru kvadratke modrega pravokotnika dimenzij 6∙5 položimo na rdeči pravokotnika dimenzij 8∙7. Preostanek rdečega pravokotnika je rezultat. V drugemprimeru storimo enako, le da je potrebno kvadratke modrega pravokotnika nekoliko preoblikovati, da "pašejo" na rdeč pravokotnik.) |
ARHIV
May 2024
KATEGORIJE
All
|

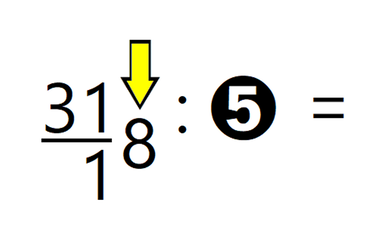





















 RSS Feed
RSS Feed
