|
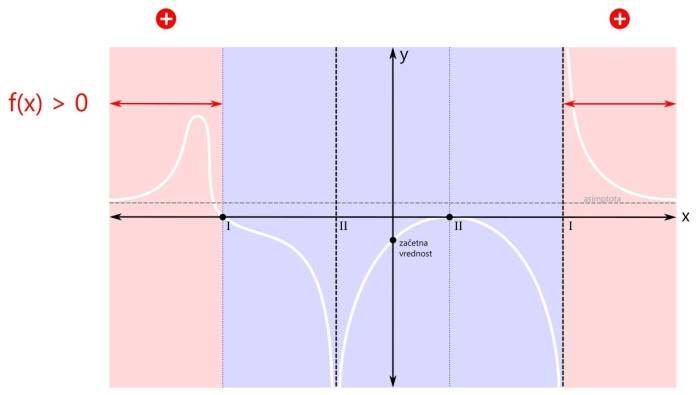
Povezavo si oglejmo kar na primeru grafa racionalne funkcije, ki smo ga narisali tule. Ogledali si bomo štiri značilne primere. V prvem primeru je pogoj za neenačbo vrednost racionalne funkcije (strogo) večje od nič. Zakaj "strogo"? Zato, ker ničla ni dovoljena ampak velja samo tisto, kar je večje od nič. Pozor! Pogoj govori o vrednostih y, medtem ko rešitev neenačbe podajamo v vrednostih x! Rešitev neenačbe običajno podajamo v enem ali več intervalih. Ker pogoj zahteva vrednost funkcije, večjo od nič, se osredotočimo na pozitivna (rdeča) področja. Taki področji sta dve, zato bosta v rešitvi dva intervala. Na sliki sta označena z rdečimi črtami, ki imata na krajiščih puščici. Zakaj puščici? Puščici na intervalu označujeta, da krajišči intervala nista vključeni v rešitev. Če bi bilo kakšno krajišče intervala vključeno v rešitev, bi bila tam pika. Na splošno so na krajiščih puščice v naslednjih primerih:
Pozor! Kadar je pogoj za neenačbo "strog", se vam ni potrebno ukvarjati z zgoraj omenjenimi pravili, ampak si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervala še z oklepaji. Pri tem upoštevamo:
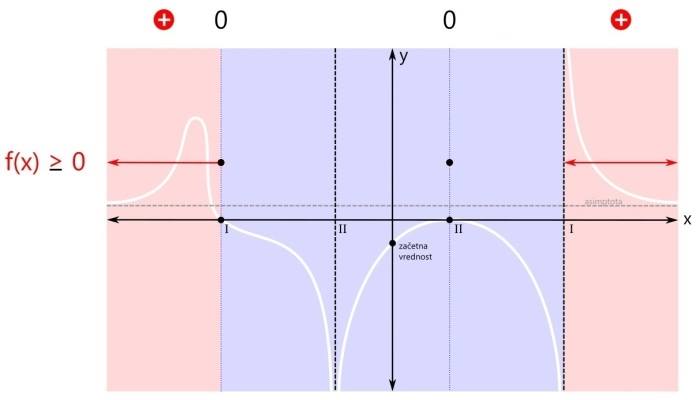
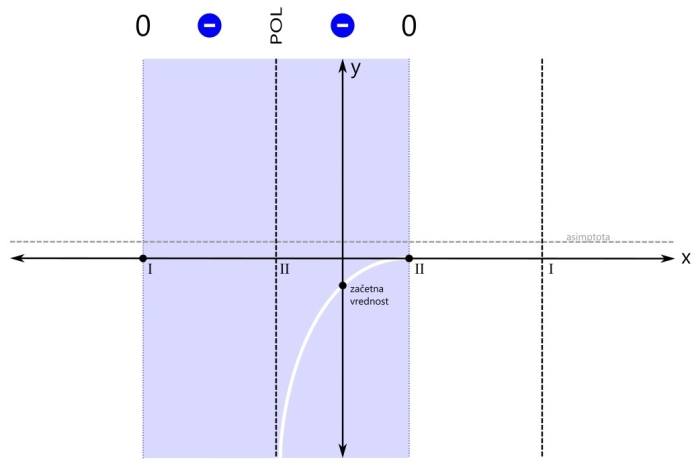
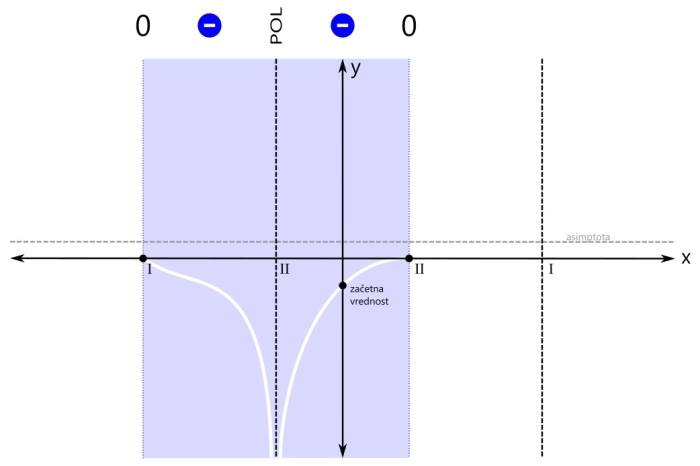
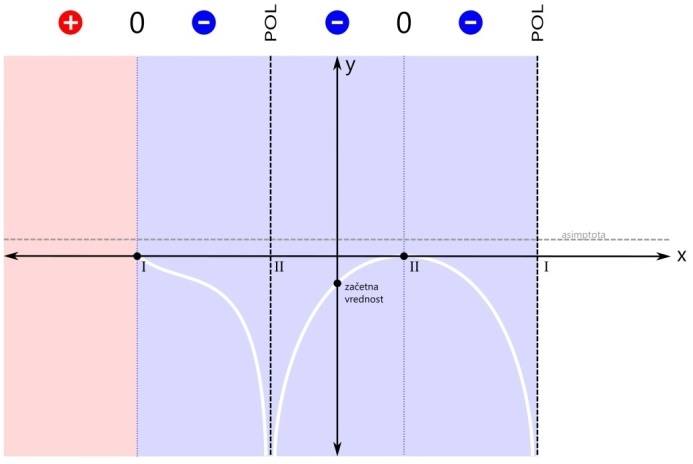
Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Med oklepaji je znak za unijo "∪". S tem znakom združimo intervale v eno rešitev. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desni pol pa na x=3, je v našem primeru rešitev naslednja: x ∈ (-∞,-3) ∪ (3,∞) V drugem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije večje ali enako nič. Od "strogega" pogoja se razlikuje v tem, da je ničla tu dovoljena. Tu pa nas zanimajo pozitivna (rdeča) področja ter ničle (črne pike):
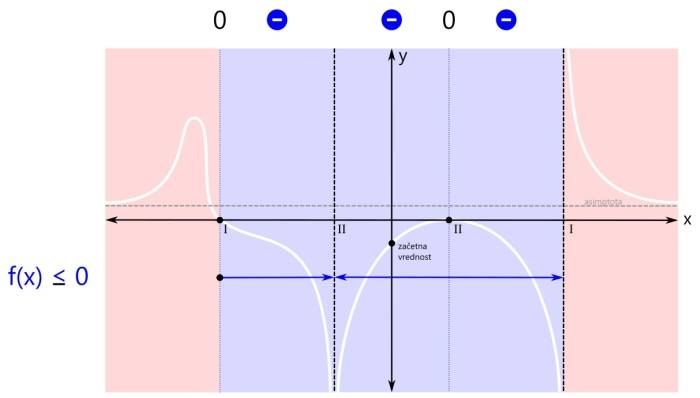
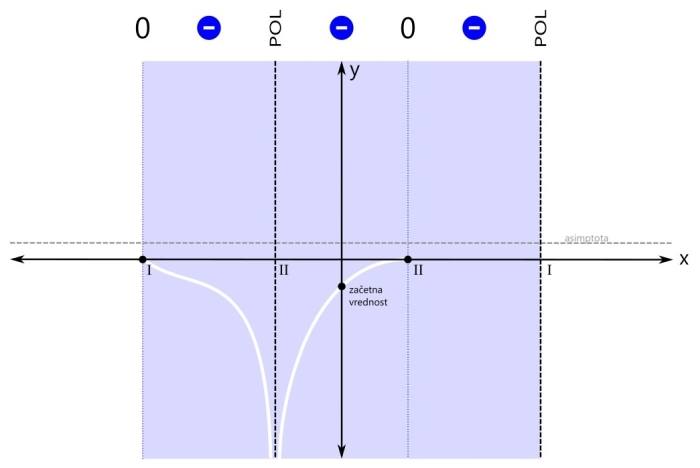
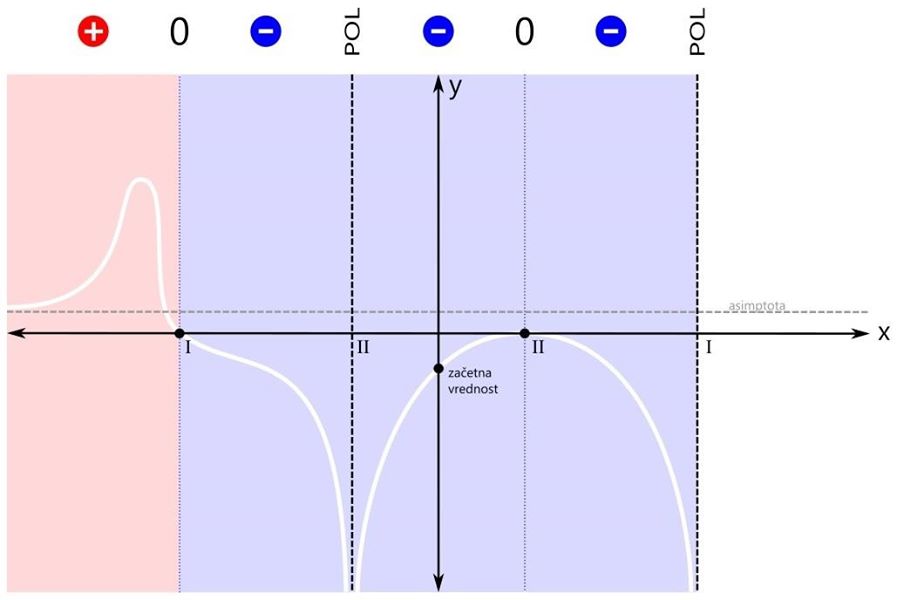
Ker sta rdeči področji dve, bosta v rešitvi dva intervala. Prva ničla (levo) je del prvega intervala (levo), zato je ni potrebno posebej navajati. Druga ničla (desno) pa je samostojna, zato jo je potrebno dodatno vključiti v rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desna ničla na poziciji x=1, desni pol pa na x=3, je rešitev naslednja: x ∈ (-∞,-3] ∪ {1} ∪ (3,∞) Pozor! Ker je rešitev v desni ničli le ena točka, je ne podamo kot interval, ampak kot zapis posameznega elementa množice rešitev - v zavitih oklepajih. V tretjem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije manjše ali enako nič. Tudi tu je ničla dovoljena. Kaj nas zanima? Negativna (modra) področja in ničle (črne pike):
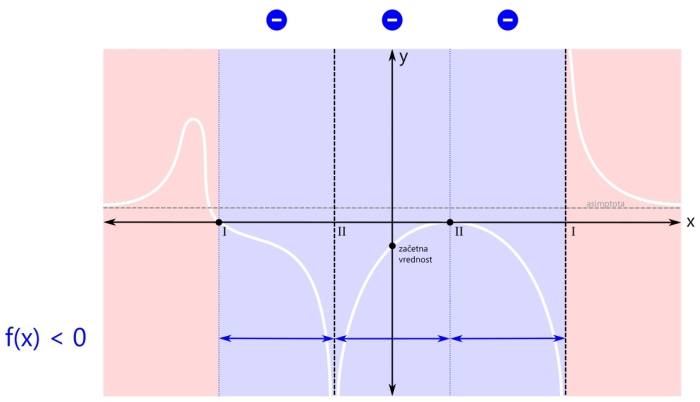
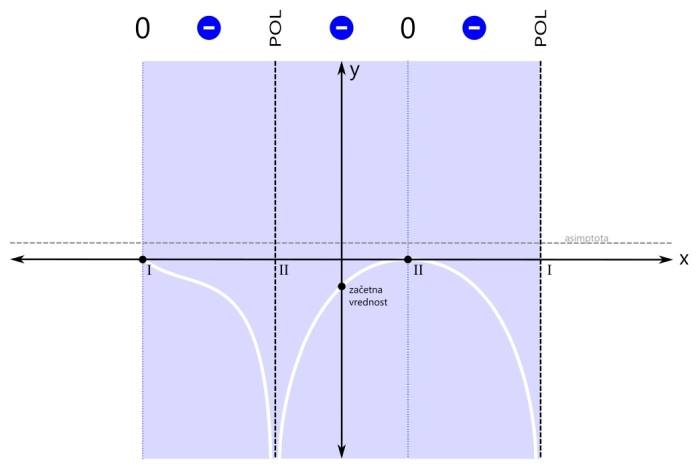
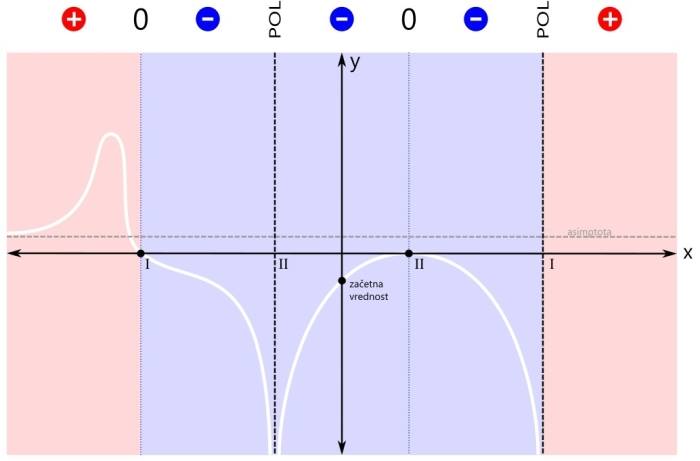
Ker so modra področja tri, bi bili v rešitvi načeloma trije intervali, a ker desna ničla združuje dva od njih, bosta v rešitvi le dva intervala. Ničla na skrajni levi pa je tudi del "modrega" intervala, tako da je ni potrebno navajati kot ločeno rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desni pol pa na x=3, je rešitev naslednja: x ∈ [-3,-1) ∪ (-1,3) V zadnjem primeru neenačbe je pogoj vrednost racionalne funkcije (strogo) manjše od nič. Tako kot v prvem "strogem" primeru tudi tu ničla ni dovoljena. Velja samo tisto, kar je manjše od nič.
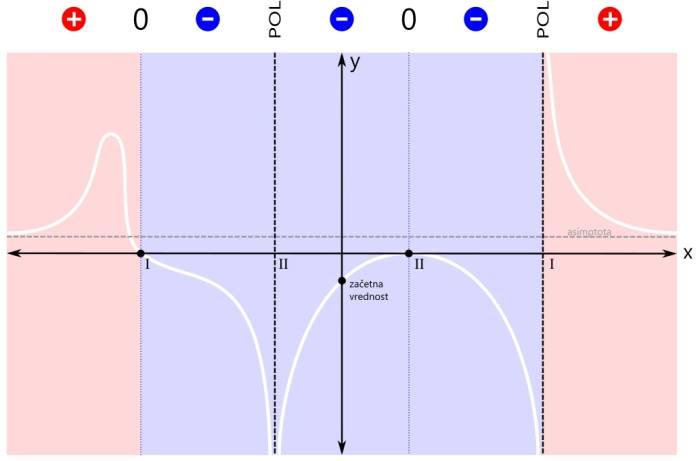
Ker pogoj zahteva vrednost funkcije, manjšo od nič, se osredotočimo na negativna (modra) področja. Tako področje je sicer eno samo, a je s polom in ničlo (druge stopnje) razdeljeno na tri dele. Rešitev bodo torej trije intervali. Na sliki so označeni z modrimi črtami, ki imajo na krajiščih puščice, kar pomeni, da krajišča intervalov niso vključena v rešitev. To, da so na krajiščih intervalov puščice in kdaj pike, smo že povedali, sedaj poudarimo samo naslednje: Pozor! Kadar je pogoj za neenačbo "strog", si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervale še z oklepaji. Ker imajo vsi intervali na krajiščih puščice, bodo vsi oklepaji okrogli. Še enkrat ponovimo naslednje splošno pravilo: Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desna ničla pa na x=1, je rešitev naslednja: x ∈ (-3,-1) ∪ (-1,1) ∪ (1,3)
0 Comments
Za vas smo pripravili "univerzalno" orodje, s katerim boste lahko kjerkoli in kadarkoli narisali graf racionalne funkcije ter reševali naloge s polinomi in racionalnimi funkcijami. Prvi se od slednjih razlikujejo predvsem po tem, da nimajo polov, s čimer so tudi njihovi grafi "lepši" :) Dobra novica pa je tudi ta, da si boste po branju tega prispevka omenjeni pripomoček lahko pripravili čisto sami :) Da bo pripomoček res univerzalen, ga pripravimo kar za racionalno funkcijo (za polinome ga bomo pa na koncu poenostavili). Naloge opisanega tipa običajno zahtevajo graf funkcije ali zapis rešitve neenačbe. Rešitev neenačbe je preprosto interval (pozor: na x osi!), kjer se graf nahaja nad ali pod določeno mejo. Predpostavimo, da ima naša racionalna funkcija dve ničli:
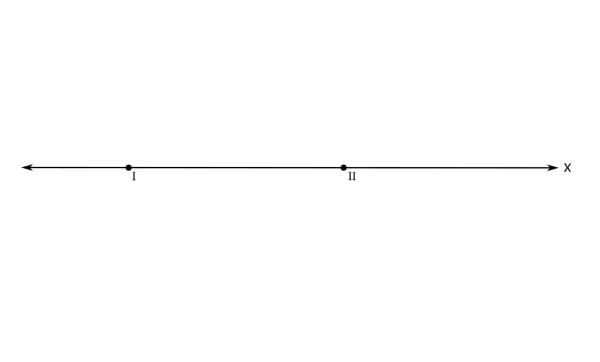
Računsko do teh ničel pridemo tako, da polinom v števcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=-3 in x₂=x₃=1. Narišimo x os in na njej označimo ničli (s pikama). Ničlo prve stopnje označimo z rimsko 1, ničlo druge stopnje pa z rimsko 2: Naša racionalna funkcija naj ima tudi dva pola:
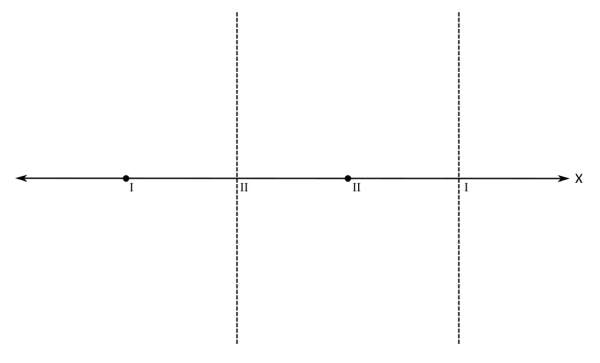
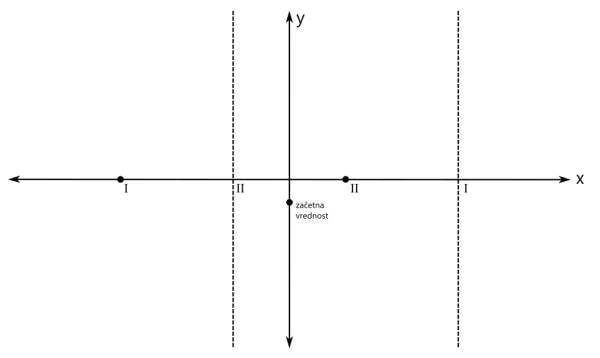
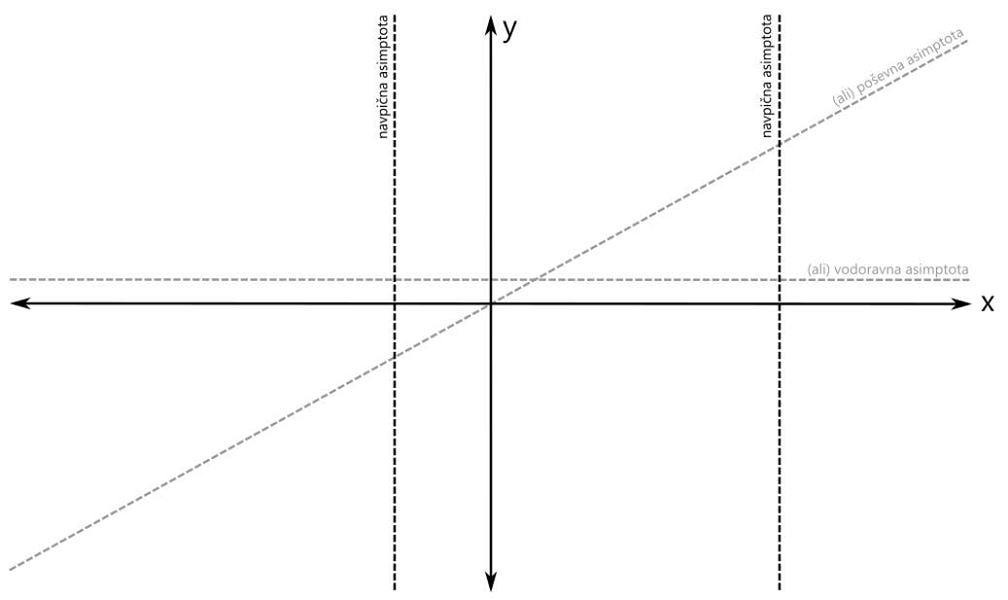
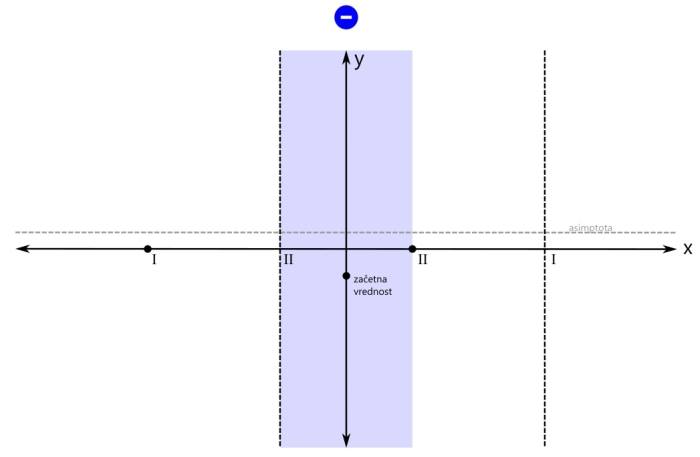
Računsko do teh polov pridemo tako, da polinom v imenovalcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Z drugimi besedami, poiščemo ničle polinoma v imenovalcu. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=x₂=-1 in x₃=3. Ampak pozor! Kljub temu, da govorimo o ničlah, so na grafu to poli, saj gre za polinom v imenovalcu! Na x osi označimo še pola (z navpičnima črtkanima črtama). Pol prve stopnje označimo z rimsko 1, pol druge stopnje pa z rimsko 2: Ničle in pole naše racionalne funkcije smo označili, sedaj je na vrsti začetna vrednost. V našem primeru je začetna vrednost negativna. Pozor! Za razliko od vrednosti ničel in polov, ki sta bili vrednosti x, je začetna vrednost vrednost y! Na primer y=-0,5. Računsko do začetne vrednosti pridemo tako, da vse x v zapisu racionalne funkcije nadomestimo z 0 in izračunamo vrednost funkcije. Z drugimi besedami, začetna vrednost je količnik prostih členov polinomov v števcu in imenovalcu. Pozor! V primerih, ko se v x=0 nahaja kakšna ničla ali pol, je potrebno izbrati novo začetno vrednost, na primer pri x=-1 ali x=1. Narišimo še y os in na njej označimo začetno vrednost: Označimo še vrednost, ki jo naša funkcija doseže pri zelo majhnih oziroma velikih vrednostih x (po domače rečeno "levo oz. desno v neskončnosti", čeprav neskončnosti dejansko ne moremo doseči). To vrednost v koordinatnem sistemu predstavlja premica (lahko je tudi krivulja, a to spada že med zahtevnejšo matematiko), ki jo graf funkcije doseže na skrajni levi oz. desni strani (v "neskončnosti"). To premico imenujemo asimptota. Le-ta je lahko vodoravna (vodoravna asimptota) ali pa poševna (poševna asimptota). Pozor! Tako kot pri začetni vrednosti nas tudi pri asimptoti zanima vrednost y! Računsko do asimptote pridemo tako, da najprej preverimo stopnji polinomov v števcu in imenovalcu racionalne funkcije (to sta najvišja eksponenta x, ki se pojavita - pri potenci x², gre recimo za polinom 2. stopnje):
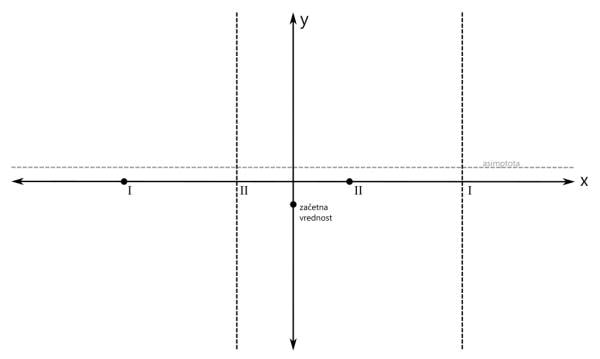
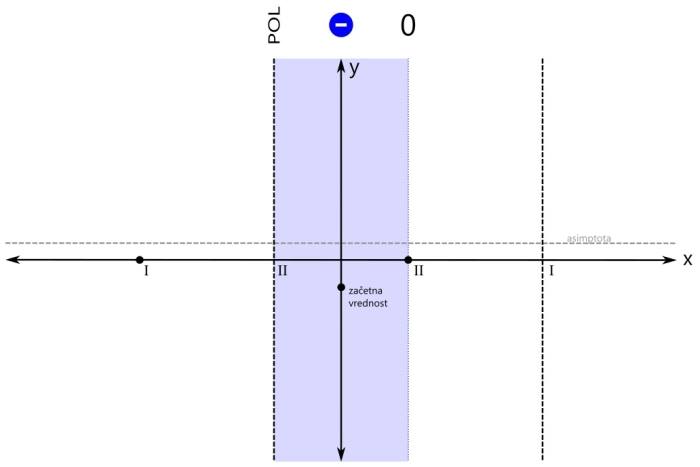
Pozor! Pri asimptoti je pomembno tudi to, da jo graf pri majhnih vrednostih x lahko seka, kar za pol recimo ne moremo reči. V našem primeru imamo vodoravno asimptoto, njena vrednost je pa večja od nič: Ustavimo se še nekoliko pri asimptotah. Po definiciji je asimptota premica ali krivulja, ki se v neskončnosti približuje drugi krivulji, ne da bi jo dosegla. Omenili smo vodoravno in poševno asimptoto. Ti dve asimptoti se nanašata na obnašanje grafa racionalne funkcije skrajno levo oziroma desno (-∞ oz. +∞ na x osi). Vodoravna in poševna asimptota hkrati ne moreta obstajati, saj se graf v neskončnosti lahko približuje le eni od njiju. Ne pozabimo: Vrednost vodoravne oz. poševne asimptote zapišemo kot y=... Pri risanju racionalne funkcije pa se skoraj vedno (kadar ima funkcija vsaj en realni pol) srečamo s še eno asimptoto, to je navpična asimptota. Ta je vedno navpična in poteka skozi pol racionalne funkcije. Navpične asimptote se nanašajo na obnašanje grafa racionalne funkcije v okolici polov (poli se nahajajo na x osi, graf pa gre v njihovi bližini navzgor ali navzdol proti neskončnosti). Navpičnih asimptot je za razliko od vodoravne in poševne lahko več - toliko, kolikor ima racionalna funkcija različnih realnih polov. Ne pozabimo: Vrednost navpične asimptote zapišemo kot x=... Navpičnih asimptot pri risanju grafa racionalne funkcije običajno ne omenjamo, le preprosto rečemo, da smo na koordinatnem sistemu označili pol racionalne funkcije. Je pa dobro, da vemo, da gre tudi v tem primeru za asimptoto. Vse asimptote rišemo kot črtkane premice. Tako, glavne značilne točke grafa imamo (stacionarne točke bomo izpustili), sedaj pa pričnimo z risanjem grafa. Graf bomo risali po odsekih, pred tem pa bomo na vsakem odseku določili predznak funkcije. Začnimo z odsekom okoli začetne vrednosti. Začetna vrednost je v našem primeru negativna, zato bo negativno tudi področje okoli nje. Za začetek z modro obarvajmo področje do prvega pola oz. ničle na levi oz. desni strani: Preverimo še predznak funkcije na robovih narisanega območja, označenega z modro barvo:
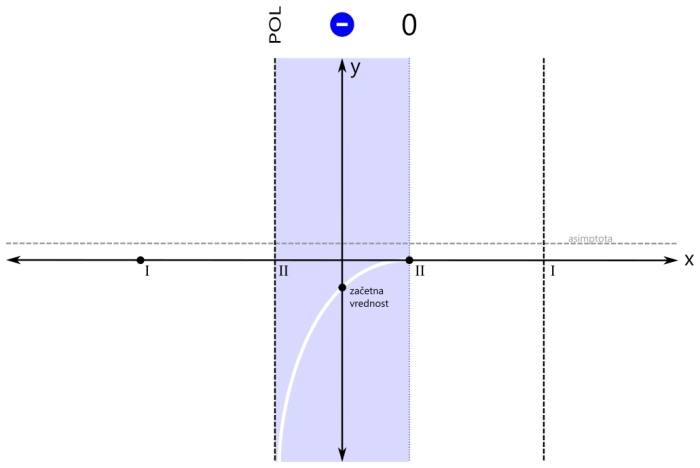
Sedaj pa pričnimo z risanjem grafa. Risali ga sproti z barvanjem območij predznaka funkcije. Zaenkrat imamo eno območje (modro). Začnimo pri začetni vrednosti. Pojdimo najprej v levo stran (do meje obarvanega območja). Ker se tam nahaja pol, graf zavije navzdol proti neskončnosti. Pozor! Navzgor graf ne more, saj bi pri tem sekal abscisno os, to pa drugje razen pri ničli ni dovoljeno! Na desni strani obarvanega območja pa imamo ničlo, zato začetno vrednost preprosto povežemo z ničlo na njeni desni. Pozor! Črta naj ne bo ravna, saj nimamo linearne funkcije! Pri risanju se izogibajmo še ostrim zavojem, pa smo že na dobri poti ;) Nadaljujemo v levo stran. Pol levo od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čezenj ne menja predznaka. Modro območje se tako nadaljuje vse do naslednje značilne točke grafa racionalne funkcije, to je ničla na skrajni levi. Vrednost funkcije v ničli pa je seveda nič ;) Nadaljujemo z risanjem grafa. Ostajamo v negativnem (modrem) območju, zato se graf vrne z iste strani, v katero je izginil, ko smo se približevali polu. Z grafom nato preprosto nadaljujemo proti ničli na levem robu modrega območja. Naj vas še enkrat opozorimo: črta naj ne bo ravna, saj nimamo linearne funkcije! Sedaj pa pojdimo še malo v desno stran. Ničla desno od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čeznjo prav tako ne menja predznaka. Negativno (modro) območje se tako nadaljuje tudi v desno - do naslednje značilne točke grafa racionalne funkcije, pola na skrajni desni. Vrednost funkcije v polu pa ni definirana. Pozor! Zaenkrat naša racionalna funkcija nikjer ni pozitivna, kar pa ne pomeni, da je vedno negativna! V ničlah je vrednost funkcije nič, v polih pa ni definirana. Z risanjem grafa nadaljujemo v desno smer. Zopet smo v negativnem (modrem) območju, zato se graf desno od ničle obrne navzdol. Nadaljujemo v desno, do meje obarvanega območja. Ker se na skrajni desni nahaja pol, graf zavije navzdol proti neskončnosti. Ničla na skrajni levi strani je lihe (prve) stopnje, zato funkcija pri prehodu čeznjo menja predznak (iz negativnega v pozitivnega). Levo od te ničle ni nobene značilne točke grafa več, zato se pozitivno (rdeče) območje nadaljuje levo v neskončnost. Narišimo še zadnji odsek grafa na levi strani koordinatnega sistema. Ker se na skrajno levi ničli predznak funkcije zamenja (iz negativnega v pozitivnega), z grafom nadaljujemo levo od te ničle navzgor. Pozor! Navzgor ne pojdimo preveč daleč, saj se graf pri zelo majhnih vrednostih x (levo v neskončnosti) približuje vodoravni asimptoti! Zato naredimo "ovinek" navzdol in z grafom funkcije nadaljujemo naprej proti asimptoti. Če želimo graf na tem (rdečem) območju še točneje narisati, si lahko izberemo kakšno dodatno točko, v kateri izračunamo vrednost racionalne funkcije in jo vrišemo na koordinatni sistem (na primer f(-4), to je vrednost funkcije pri x=-4). Določimo predznak še na zadnjem območju grafa racionalne funkcije. Pol na skrajni desni strani je lihe (prve) stopnje, zato funkcija pri prehodu čezenj menja predznak (iz negativnega v pozitivnega). Desno od tega pola ni nobene značilne točke grafa več, zato se pozitivno (rdeče) rdeče območje nadaljuje desno v neskončnost. Narišimo še zadnji odsek grafa na desni strani koordinatnega sistema.
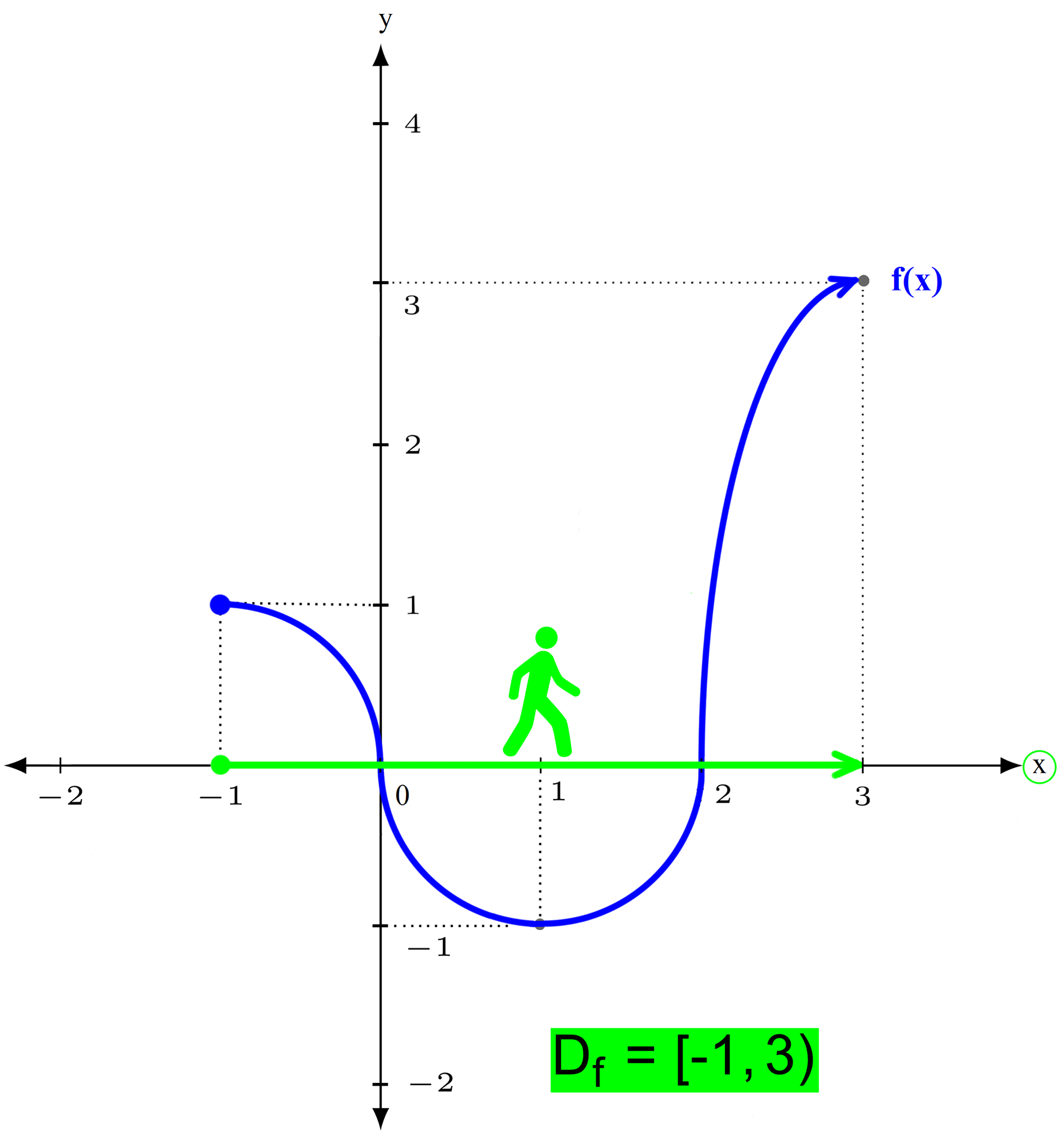
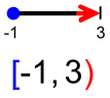
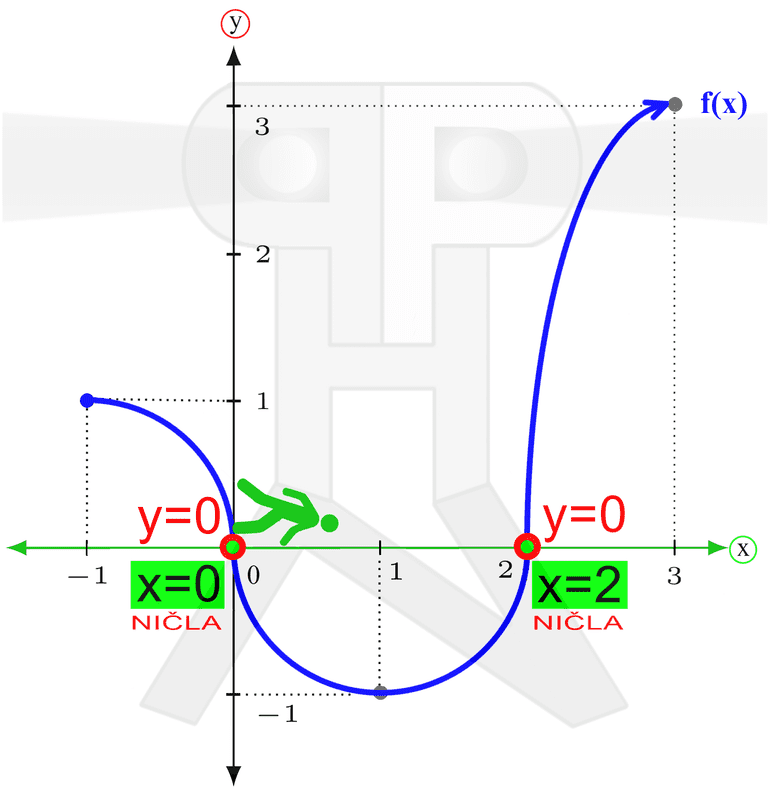
Ker se na skrajno desnem polu predznak funkcije zamenja (iz negativnega v pozitivnega), se graf na drugi strani pola ne vrne z iste strani, v katero je izginil (navzdol), ampak z nasprotne (od zgoraj). Ker se graf racionalne funkcije pri zelo velikih vrednostih x (desno v neskončnosti) približuje vodoravni asimptoti, le-ta naredi zavoj v desno (brez ostrih robov!) in se nadaljuje naprej proti asimptoti. Pozor! Abscisne osi (x) na tem odseku ne smemo več sekati, saj v področju desno od pola prve stopnje ni več nobene ničle, graf pa lahko seka abscisno os le pri prehodu preko ničle! Ste se kdaj "zataknili" pri definicijskem območju ali zalogi vrednosti? Govorimo seveda o funkcijah, takih in drugačnih, vsaki z zvrhanim košem lastnosti :) Da pred tablo ali na pisnem testu ne boste "debelo gledali", vam predstavimo nekaj idej, kako funkciji določiti lastnosti na čim lažji način. Definicijsko območje Začnimo z definicijskim območjem, ki smo ga malo prej že omenili. Kot vemo, funkcija preslika neodvisno spremenljivko (največkrat je to x) v odvisno spremenljivko (običajno y). In definicijsko območje pomeni tiste vrednosti x, ki se bodo preslikale v y. Jap, ne pridejo vedno vse na vrsto za preslikavo ;) Definicijsko območje si je najlažje predstavljati na grafu funkcije. Zamislite si, da ste možak na spodnji sliki. Hodite po abscisi koordinatnega sistema (to je x os) od leve proti desni strani (v tej smeri tudi pišemo). Pri hoji se ozirate navzgor in navzdol, če boste kje videli funkcijo. Del poti, kjer je funkcija vidna, pobarvate z zeleno (tako kot je označeno na spodnji sliki). Interval, ki ste ga narisali (obarvan zeleno), je definicijsko območje funkcije:
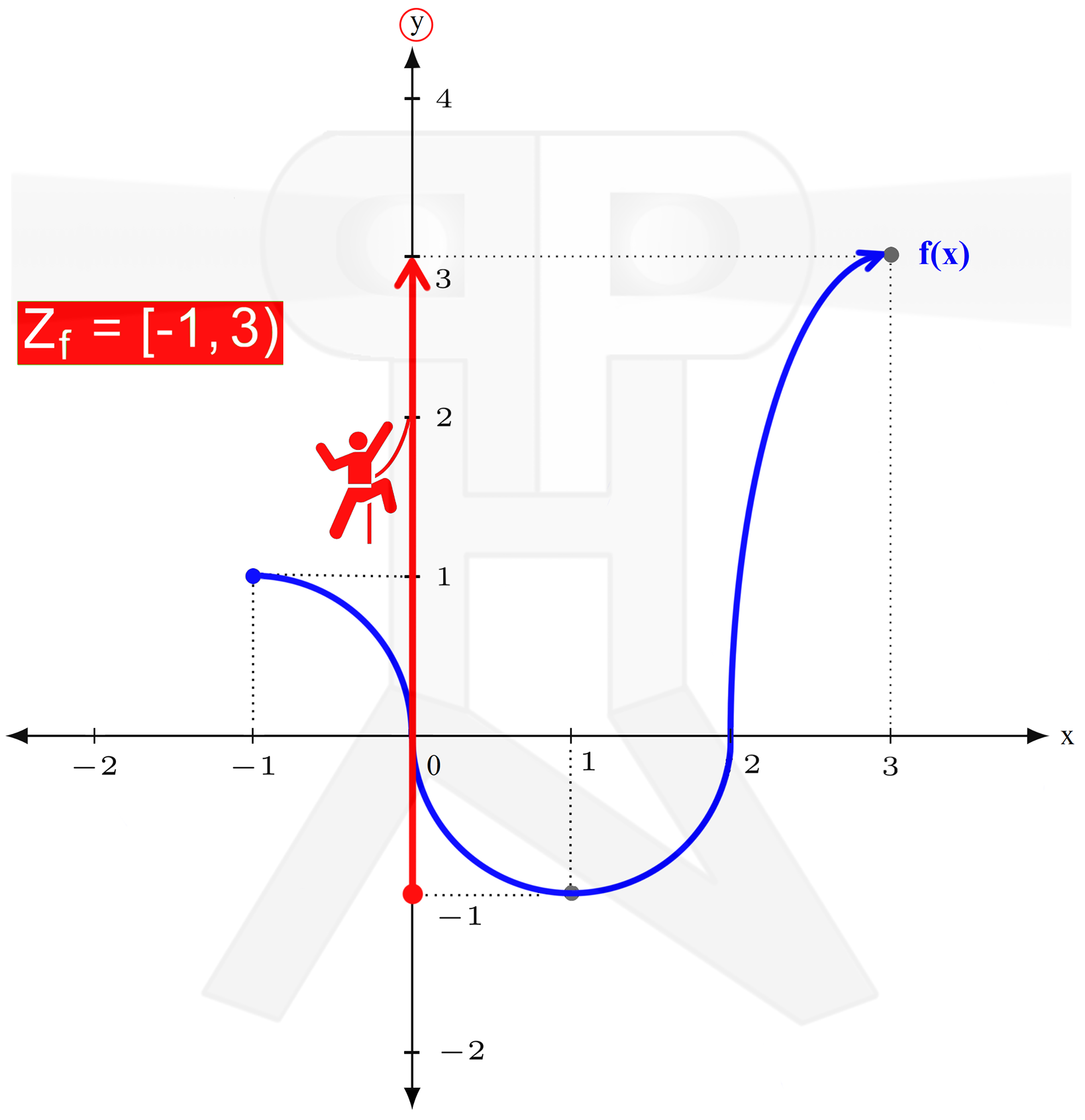
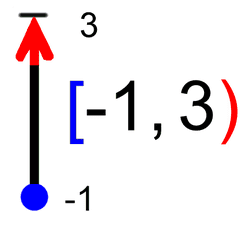
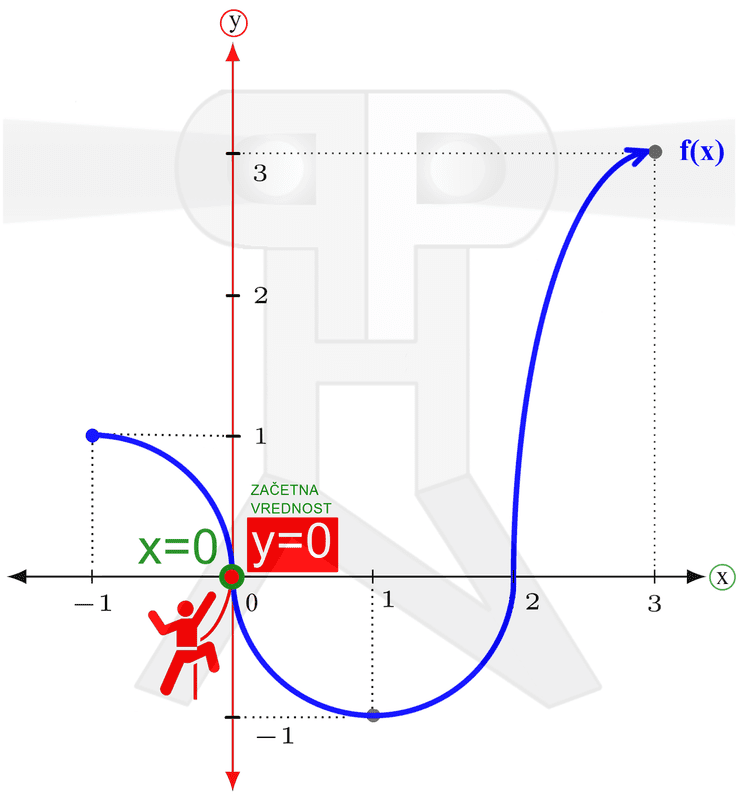
V našem primeru začetna točka spada zraven, končna pa ne. Temu primeren je tudi zapis definicijskega območja. Zaloga vrednosti Poleg definicijskega območja običajno vedno navedemo tudi zalogo vrednosti. Če so definicijsko območje tiste vrednosti x, ki se bodo preslikale v y, so "zaloga vrednosti" vse vrednosti y, ki so pri preslikavi nastale. Poenostavljeno bi lahko rekli, da se je definicijsko območje preslikalo v zalogo vrednosti. Tudi zalogo vrednosti si najlažje predstavljamo na grafu funkcije. V prejšnjem poglavju smo bili "zelen sprehajalec", sedaj pa bodimo "rdeč plezalec" ;) Včeraj smo hodili, danes pa plezamo, navpično navzgor, po ordinati koordinatnega sistema (y os). Plezati začnemo v najnižji točki grafa funkcije in splezamo vse do njenega vrha. Ker nam plezanje ne dela težav, zraven še malo pleskamo, tokrat z rdečo barvo :)
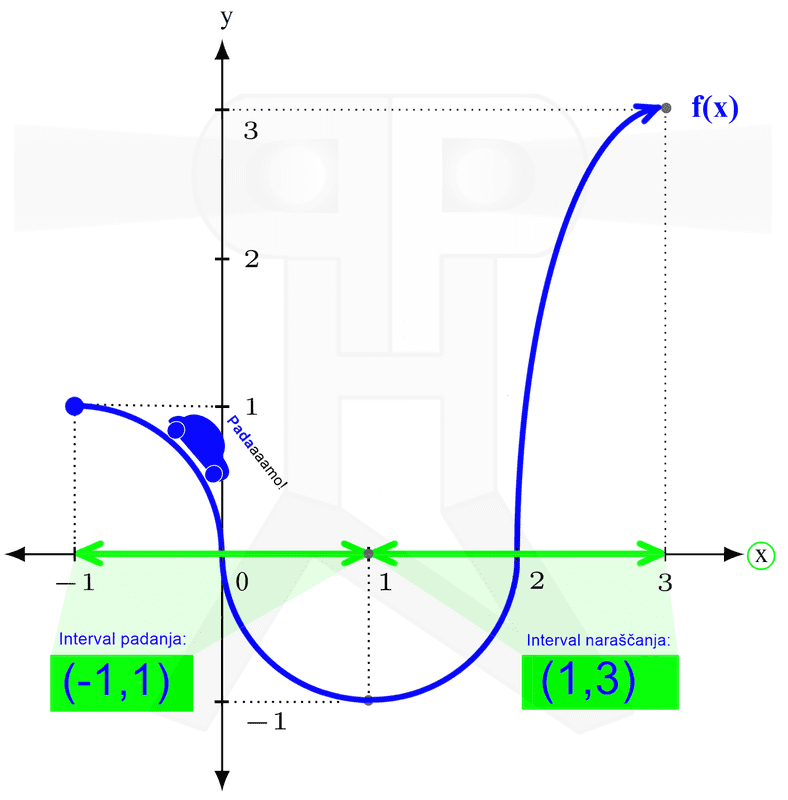
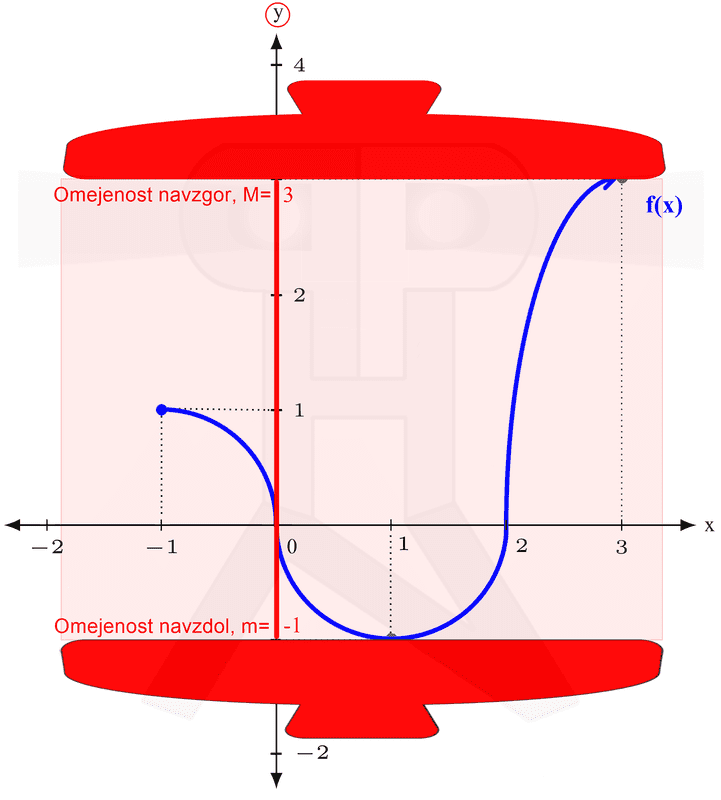
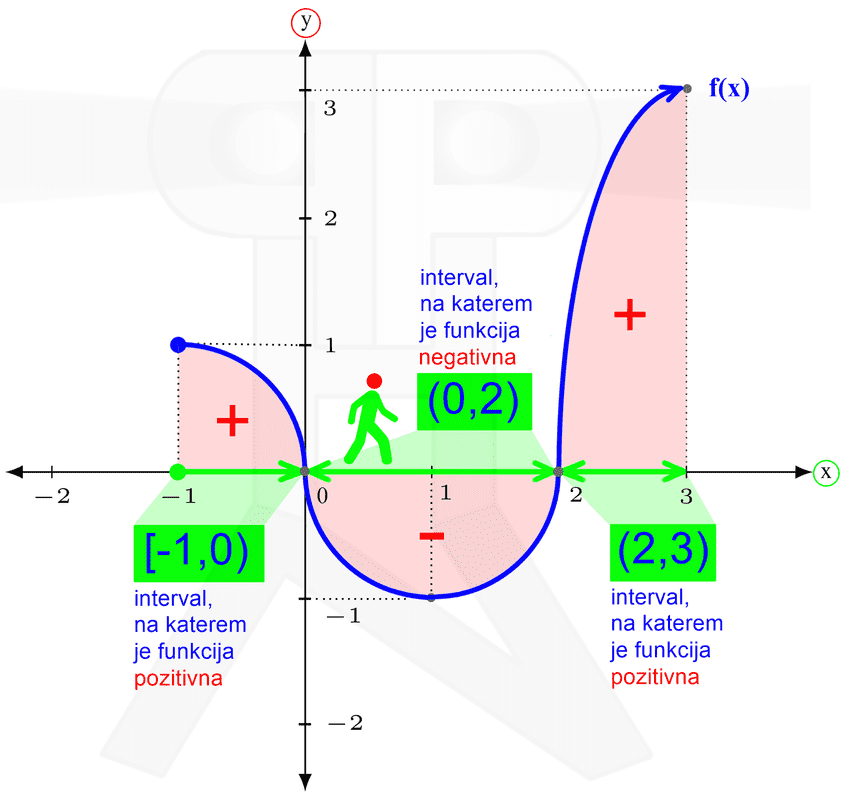
V našem primeru najnižja točka spada zraven, najvišja pa ne. Temu primeren je tudi zapis zaloge vrednosti. Naraščanje in padanje Na kratko: zanima nas, pri katerih vrednostih (neodvisne) spremenljivke x funkcija narašča in pri katerih vrednostih pada. Vrednosti spremenljivke x seveda ne naštevamo, ker bi jih bilo preveč, ampak jih podajamo v obliki intervalov. Spremenljivki x pripadajo "vodoravni" intervali, ki smo jih srečali že pri obravnavi definicijskega območja in so na naših slikah obarvani zeleno. Intervale naraščanja in padanja najlažje razberemo z grafa funkcije. Do sedaj smo tekli in plezali, tokrat pa se peljimo z avtomobilom. Peljemo se po (modri) krivulji funkcije od leve proti desni (v tej smeri tudi pišemo) in smo pozorni na to, ali se peljemo "v klanec" ali "s klanca". Ko gremo navzgor, funkcija narašča, ko gremo navzol, pa pada: Naj omenimo še to, da točke, kjer graf iz padanja preide v naraščanje (in obratno), ne spadajo v intervale naraščanja oz. padanja, zato so oklepaji v zapisu intervalov vedno okrogli. Ne pozabimo: če graf "pride iz neskončnosti" oziroma "gre v neskončnost", moramo pa tako ali tako uporabiti okrogli oklepaj! Omejenost Funkcija je lahko omejena navzgor, navzdol ali pa kar v obe smeri (in ne na levo in desno, kot se včasih kdo rad zmoti). Vsi ste že kdaj merili svojo višino. Če ne drugače, so vas izmerili na sistematskem pregledu. Na podoben način lahko "izmerimo" tudi funkcijo, s to razliko, da ne bomo podali njene višine, ampak le najnižjo in najvišjo točko. Zopet si pomagajmo z grafom funkcije. Zamislimo si dve veliki pokrovki (na sliki rdeče barve), med kateri "ulovimo" funkcijo. Zakaj ravno pokrovki? Zato, da bo zares "odbito" in si boste zato bolj zapomnili :) Položaj spodnje pokrovke na navpični (y) osi nam pove spodnjo mejo funkcije (označimo jo z malo črko m), položaj zgornje pokrovke na y osi pa nam pove zgornjo mejo funkcije (označimo jo z veliko črko M). Včasih se zgodi, da funkcije ne moremo "ujeti v pokrovko". V tem primeru funkcija navzdol oz. navzgor ni omejena. Kakšne niso omejene navzgor, druge navzdol, se pa najdejo tudi take, ki sploh niso omejene. Pozitivnost in negativnost Poglejmo, pri katerih vrednostih x je funkcija pozitivna oziroma negativna. Tudi tu vrednosti spremenljivke podajamo v obliki intervalov ("vodoravni" intervali, obarvani zeleno) Spomnimo se poglavja o definicijskem območju, kjer se je zelen možak oziral navzgor in navzdol ter preverjal, kje je funkcija vidna. Takrat ga ni zanimalo, ali je funkcija nad ali pod njim, sedaj pa je to pomembno (zato smo možaku glavo obarvali rdeče). Kadar je funkcija nad možakom, je le-ta pozitivna, kadar pa je pod njim, pa je negativna: Točke, kjer graf seka x os, ne spadajo v intervale pozitivnosti oz. negativnosti (uporabimo okrogli oklepaj!), saj tam funkcija ni ne pozitivna in ne negativna, ampak je njena vrednost enaka nič. Te točke imenujemo ničle funkcije. K njim se še vrnemo v nadaljevanju. Ne pozabimo: Če graf "pride iz neskončnosti" in/ali "gre v neskončnost", moramo na začetku prvega in/ali na koncu zadnjega intervala uporabiti okrogli oklepaj! Ničle funkcije Nekaj vrstic nazaj smo iskali vrednosti (neodvisne) spremenljivke x, pri katerih je funkcija pozitivna oziroma negativna. In kakšno vrednost ima funkcija, če ni niti pozitivna, niti negativna? Nič, seveda :) Točke, v katerih ima funkcija vrednost 0, imenujemo ničle funkcije. Nahajajo se na abscisni (x) osi koordinatnega sistema. Ne pozabimo: v ničlah je y enak 0, medtem ko vrednost "ničle" pove x! Na grafu ničle funkcije izgledajo kot neki kamni na zeleni poti (vodoravna x os), ob katere se spotika naš možic, ki smo ga že kar nekajkrat srečali: V ničli graf seka ali pa se dotika (zeleno označene) x osi. Graf seka x os v ničlah "lihega reda" (stopnje 1,3,5,...), dotika se ga pa v ničlah "sodega reda" (stopnje 2,4,6,...). V našem primeru sta ničli dve. Prva ima vrednost 0, druga pa vrednost 2. Označeni sta z zelenim okvirčkom. Začetna vrednost funkcije V nasprotju z ničlami, ki smo jih obravnavali nekaj vrstic višje, tokrat 0 ni vrednost funkcije, ampak vrednost neodvisne spremenljivke x. Ne pozabimo: v točki, ki označuje začetno vrednost, je x enak 0, medtem ko začetno vrednost podajamo z y! Na grafu začetna vrednost izgleda kot nek "oprijemek" na rdeči steni (navpična y os), po kateri pleza naš možic, ki smo ga že kar nekajkrat srečali: V tej točki, ki označuje začetno vrednost, graf funkcije seka (rdeče označeno) y os.
V našem primeru je začetna vrednost enaka 0. Označena je z rdečim okvirčkom. Jih znate našteti? ;) Še enkrat jih ponovimo posebej za vas:
Eksplicitna oblika zapisa enačbe premice Najprej razrešimo dilemo med eksplicitnim in implicitnim zapisom. Besedi seveda izvirata iz latinščine, v oči oziroma ušesa pa nas najbolj zbode predpona pri prvi, to je "eks-", ki po latinsko pomeni "izven" oziroma "iz". Kdo je v tem primeru "zunaj"? Odvisna spremenljivka y. Na drugo stran enačaja jo je namreč postavila neodvisna spremenljivka x v družbi koeficientov (številk). To je nekako tako, kot da bi "eks" dekle pred vrata postavilo "eks" fanta. Auč, not good. Na sliki imate primer eksplicitnega zapisa: Implicitna oblika zapisa enačbe premice Če je pri eksplicitnem zapisu odvisna spremenljivka y osamljena, ločena od neodvisne spremenljivke x in številskih koeficientov, je pri implicitnem zapisu le-ta "v dobri družbi". Na drugi strani enačbe pa je ničla, po čemer tak zapis linearne funkcije tudi najlažje prepoznamo. Če še malo "pokukamo" k latinščini, beseda eksplicitno izhaja iz latinskega izraza "implicitus", ki pomeni "vključiti, prepletati" - logično, spet je govora o odvisni spremenljivki y, ki tokrat ni osamljena (juhu :)) Odsekovna oblika zapisa enačbe premice
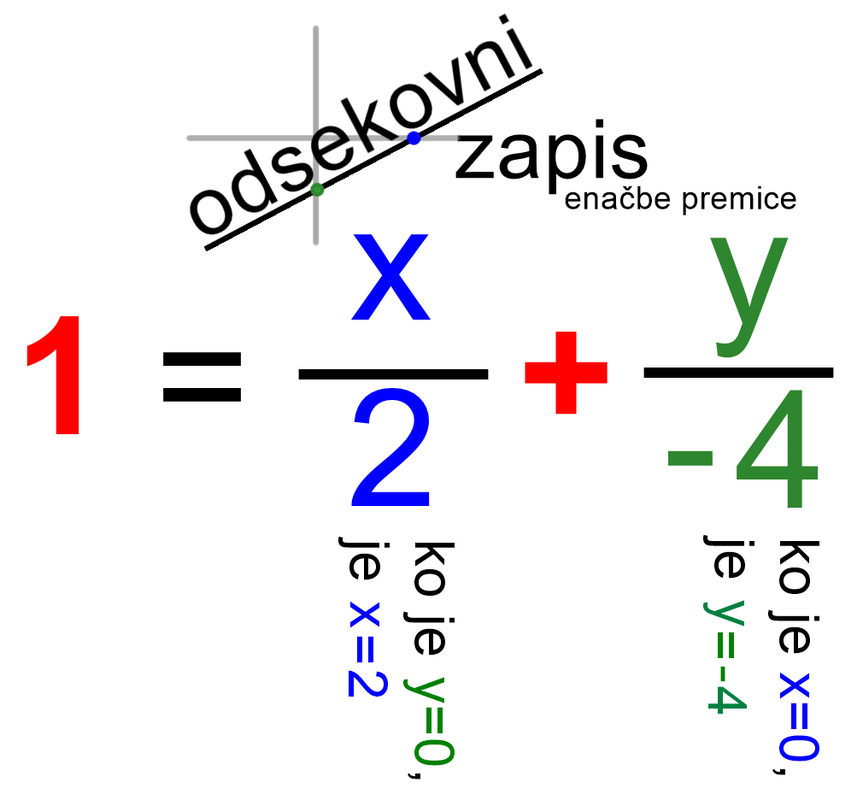
Ta zapis je po eni strani najbolj zakompliciran, po drugi strani pa si ga je najlažje predstavljati, saj je v neposredni povezavi z grafom funkcije. Tokrat je na svoji strani enačbe "osamljena" enica. Kaj nam ta enica pove?
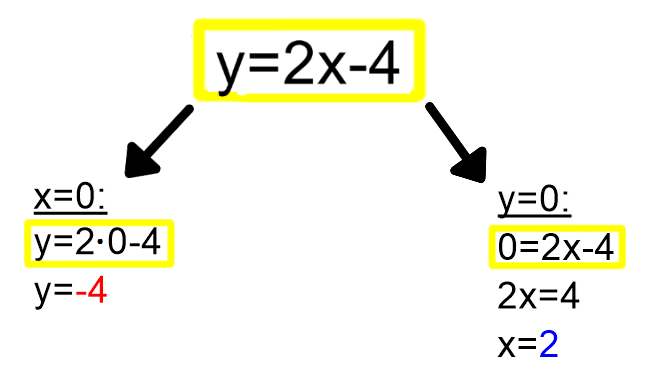
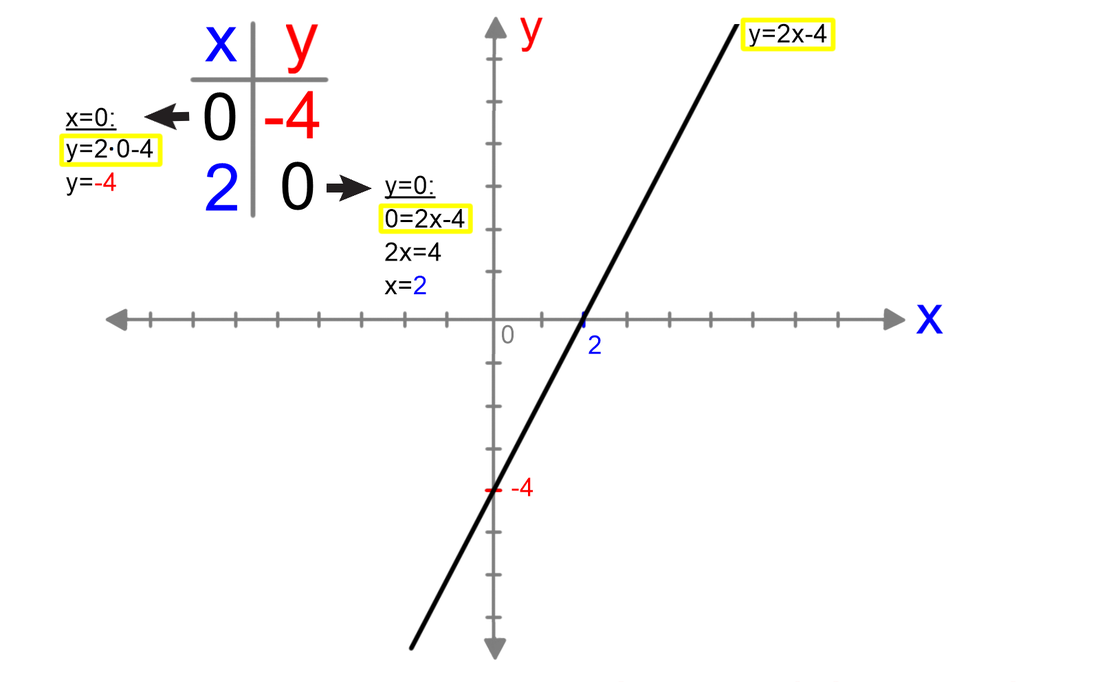
Načinov za risanje grafov linearnih funkcij je več; z enimi pokažete več znanja (ki ga tudi hitro pozabite), drugi so pa bolj enostavni, a jih zlepa ne pozabite. Pobliže poglejmo enega od slednjih. Narišimo graf linearne funkcije y=2x+4. Vemo, da ima linearna funkcija dve spremenljivki. Ena je neodvisna (x), druga pa je odvisna (y). Vse, kar morate storiti je, da vsako od njiju izenačite z nič in preverite, kakšno vrednost ima pri tem druga spremenljivka: S tem, ko smo vrednost spremenljivk x in y postavili na 0, smo dobili dve točki na koordinatnem sistemu. Ker imata vsaka eno od koordinat enako 0, ležita vsaka na eni od koordinatnih osi in ju je zato lahko označiti. Skoznji potegnemo le še premico in že imamo graf linearne funkcije. Naj na koncu opozorimo, da omenjena metoda ni primerna za grafe funkcij, ki potekajo skozi koordinatno izhodišče, saj v tem primeru omenjeni točki sovpadata (0,0).
Iz težav nas reši tretja točka, katere koordinate dobimo tako, da si izberemo poljuben x (npr. 1), ga vstavimo v funkcijo in izračunamo vrednost y. Sedaj potegnemo le še premico skozi koordinatno izhodišče in to tretjo točko (1, izračunan y), in graf je tu. |
ARHIV
May 2024
KATEGORIJE
All
|



 RSS Feed
RSS Feed
