V matematiki najdemo veliko računskih operacij, ki so med seboj obratne. To pomeni, da rezultat prve operacije z drugo operacijo vrnemo nazaj v začetno stanje. Vsakdo od vas bi si verjetno želel matematične operacije, ki bi vašo razmetano sobo pospravila nazaj v "pospravljeno stanje" ;)

"In kje je sedaj tisti del, ki pravi, da se je potrebno naučiti samo na pol?" boste dejali. Če sta računski operaciji obratni, je dovolj, da se določenega postopka naučimo le za prvo, za drugo pa vemo, da omenjeni postopek "obrne na glavo".

Oglejmo si primer. Množenje in deljenje sta obratni računski operaciji. Če vemo, da vsako množenje z 10 rezultatu doda ničlo (oziroma decimalno mesto premakne v desno), jo bo vsako deljenje z 10 odvzelo (oziroma decimalno mesto premaknilo v levo).

Naštejmo nekaj najbolj pogosto uporabljanih računskih operacij, ki so med seboj obratne:

• seštevanje in odštevanje
• množenje in deljenje
• potenciranje in korenjenje
• odvajanje in integriranje

Oglejmo si še en primer za potenciranje in korenjenje, konkretno za kvadrat in kvadratni koren:

• ker je 5²=25,
  je 50² = 2500 (kvadrat podvoji število ničel)
  oziroma je 0,5² = 0,25 (kvadrat podvoji število decimalnih mest)
• za koren velja pa ravno obratno; ker je √25 = 5
  je √2500 = 50 (koren razpolovi število ničel)
  oziroma je √0,25 = 0,5 (koren razpolovi število decimalnih mest)

Včasih dve obratni računski operaciji najdemo kar v enem računu, česar se še posebej razveselimo, saj ena operacija izniči drugo, tako da nam sploh ni potrebno ničesar računati :)

Oglejmo si nekaj primerov:

• √(0,25)² = 0,25, saj kvadratni koren izniči kvadrat;

• a + 5b - 5b = a, saj enako vrednost (5b) najprej prištejemo in nato odštejemo;

• abc / abd = c / d, saj enako vrednost (ab) v števcu in imenovalcu ulomka okrajšamo.

Ste vedeli, da se je tudi poštevanke dovolj naučiti le na pol? Za to pa ima zaslugo zakon o zamenjavi, ki velja za množenje. 3·4 je tako enako 4·3 in tako naprej ... Zakon o zamenjavi velja tudi za seštevanje.

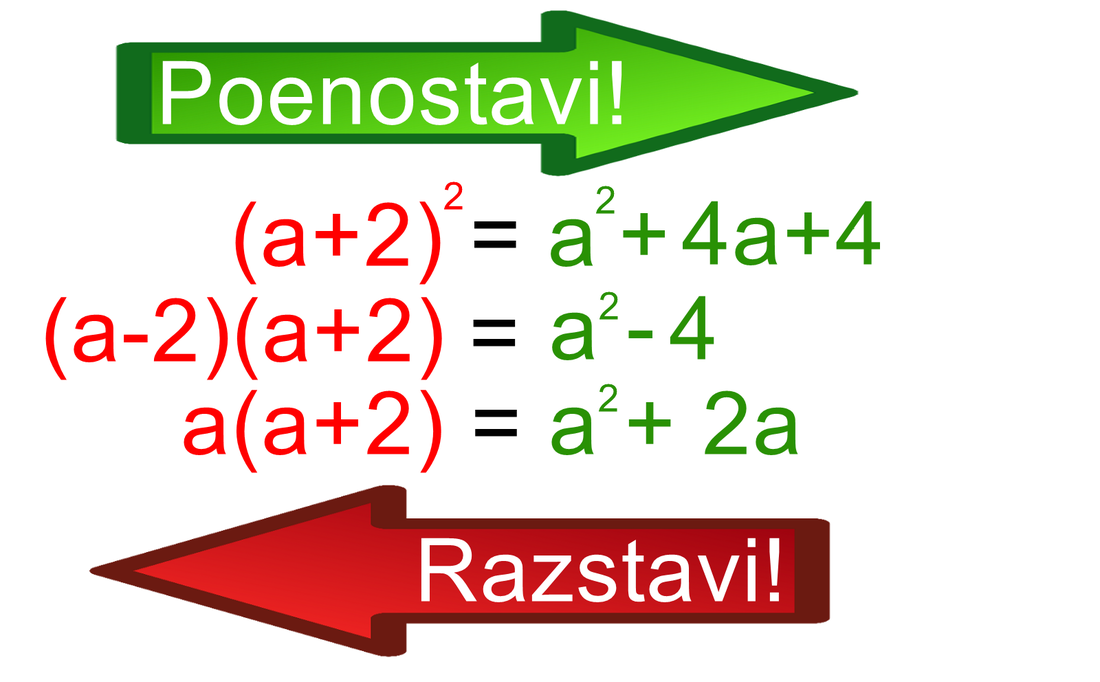
Navodila, ki sledijo, vam bodo prišla prav pri domačih nalogah ter matematičnih testih, tudi na NPZ-jih ter maturi.

A veste, tisto, ko si ves nervozen, do konca testa je le še 10 minut, pa ne veš točno, kaj naloga sploh hoče od tebe?!? No, tega, upamo, da bo sedaj manj ;)

Poenostavi!

Pri taki nalogi najprej z množenjem in potenciranjem odpravimo oklepaje (izraz razširimo), na koncu pa "zložimo" skupaj podobne člene ter konstante:

V šali včasih kdo reče: "Pa ne moreš seštevati jabolk in hrušk!" In prav ima! Hrušk in jabolk seveda ne moremo sešteti skupaj, lahko pa seštejemo oziroma odštejemo vsake posebej.

V nalogah lahko namesto "Poenostavi!" zasledimo zahtevo "Skrči izraz!" Navodili za reševanje sta pri obeh enaki. Enemu učitelju je pač bolj všeč en, drugemu pa drug način podajanja navodila za reševanje naloge.

Razstavi!

V matematiki ima (skoraj) vsaka operacija svojo inverzno operacijo. Naj navedemo nekaj takšnih "parov":

• seštevanje in odštevanje
  
• množenje in deljenje
  
• potenciranje in korenjenje
• itd.

Tako ima tudi navodilo "Poenostavi!" svojo inverzno različico, ki se glasi: "Razstavi!" Razliko med njima najbolje ponazorijo naslednji primeri:

Pomembno je, da si zapomnite naslednje:

• poenostavljena oblika izraza nima oklepajev, razstavljena pa jih ima
• po obliki poenostavljena oblika izgleda kot neka "kača" (niz členov, ločen s plusi in minusi), razstavljena pa je en sam člen, sestavljen iz oklepajev.
• pri poenostavljanju največ množimo in potenciramo, pri razstavljanju pa izpostavljamo

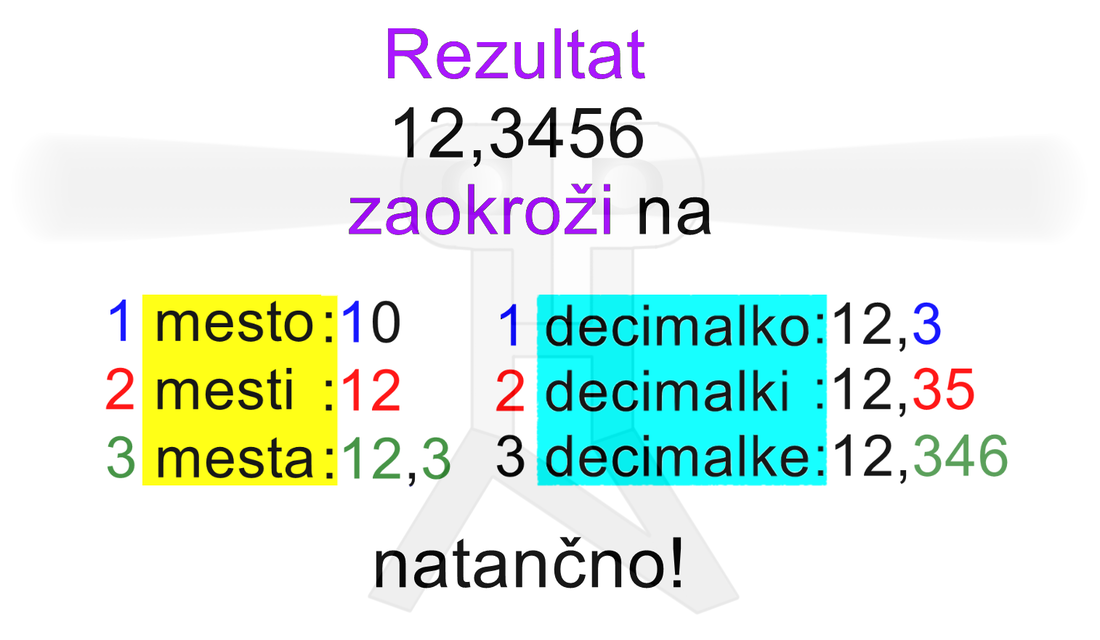
Reši!

Kaj lahko na matematičnem testu "rešimo"? Enačbo ali neenačbo. In zakaj ravno "rešimo"? Predstavljajte si, da ste superjunak, ki iz krempljev strašne enačbe rešite spremenljivko (največkrat je to "x"). No, sedaj ste dobili odgovor :)

Reševanje (ne)enačb je podobno kot poenostavljanje izrazov, s to razliko, da imamo pri (ne)enačbah nekaj členov na levi in nekaj členov na desni strani (ne)enačaja, medtem ko je pri izrazih vedno vse na levi strani enačaja, kar ponazarja tudi primer:

Če naredimo preizkus, vedno vemo, koliko točk bomo dobili pri taki nalogi, še preden jo učitelj(ica) preveri oziroma "popravi", kot včasih radi rečemo.

Izračunaj!

Če moramo nekaj izračunati, v rezultatu dobimo same številke. Tudi rešitev (ne)enačbe je številka, kot smo videli včeraj.

Za primerjavo: pri poenostavljanju v rezultatu poleg številk dobimo tudi spremenljivke (x, y, a, b,...) - razen takrat, ko se le-te okrajšajo:

Nekatere naloge so pa še bolj "zvite": izraz moramo najprej poenostaviti, nato pa ga za podane številske vrednosti spremenljivk še izračunamo.

Zaokroži!

Če je rezultat realno število (ima neskončen decimalni zapis), ga lahko zapišemo točno ali pa ga zaokrožimo.

Najprej si oglejmo zaokrožanje. Rezultat lahko zaokrožimo na dva načina:

• na številska mesta (gledamo števke od prve neničelne naprej)
• na decimalna mesta (gledamo števke za decimalno vejico)

Pri zaokroževanju je potrebno vedno "pokukati" še za eno mesto naprej (desno od zadnje števke, ki nas še zanima):

• če je na tem mestu števka od 0 do 4, odvečna mesta preprosto "odrežemo"
• ​če je na tem mestu števka od 5 do 9, zadnjo števko, ki nas še zanima, povečamo za 1 oziroma "zaokrožimo navzgor".

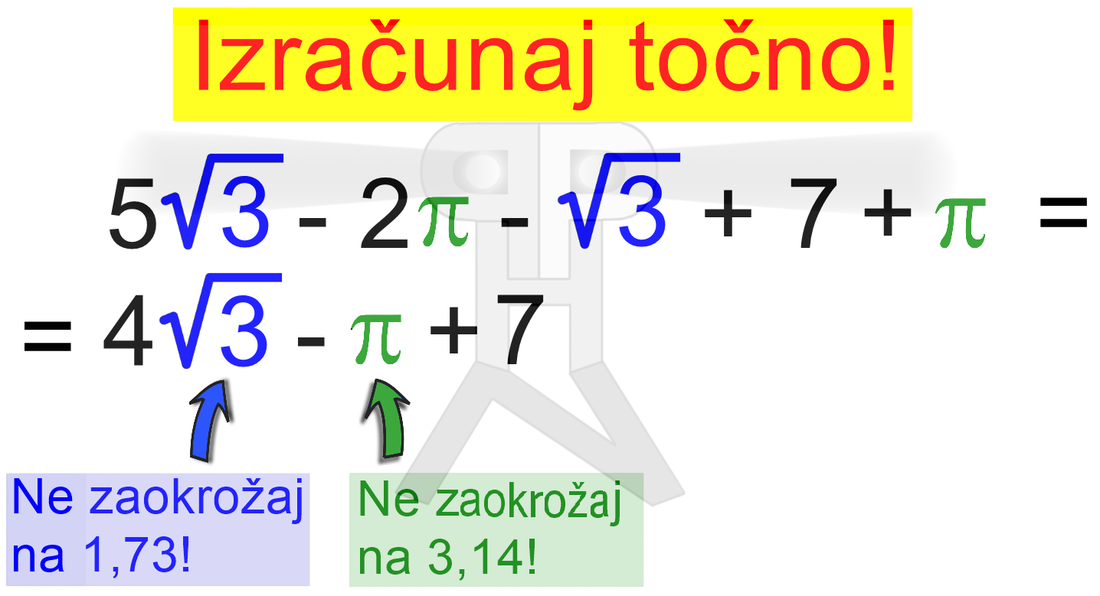
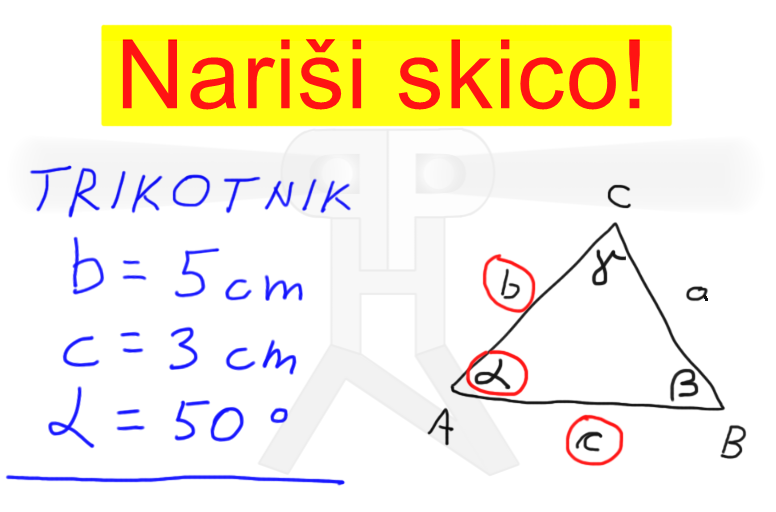
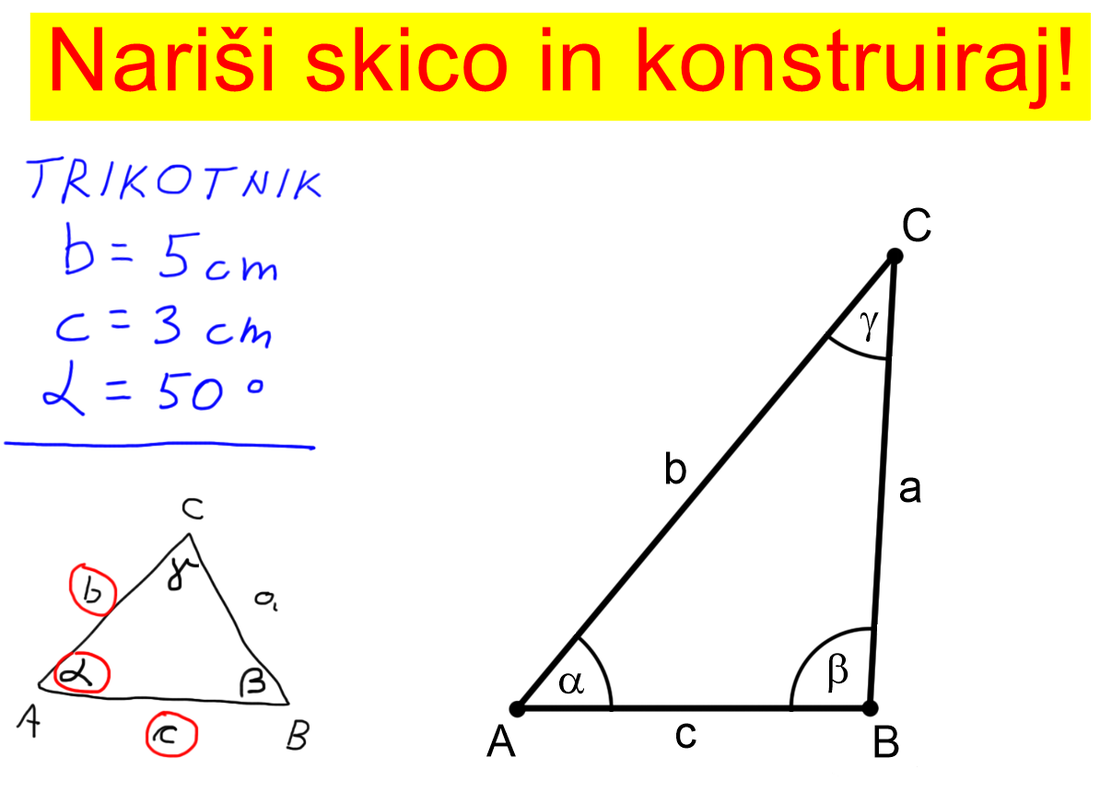
Izračunaj točno!

Če želimo rezultat, v katerem nastopajo koreni ter matematične konstante, ki se jih ne da zapisati brez zaokrožanja (npr. π ali e), zapisati točno oz. natančno, teh števil ne smemo zaokrožati, ampak jih pišemo v prvotni obliki, torej koren ostane koren, posebna števila pa ostanejo zapisana z znakom, ki jih določa.

Ne pozabimo pa izraza s takimi števili poenostaviti, torej sešteti oziroma odšteti vse enake korene ter posebna števila: