Znak za računsko operacijo oziroma predznak "pripada" vedno tistemu, ki je na njegovi desni strani26/12/2017 Seštevanje in odštevanje (oziroma predznak + in -)
Marsikaterega učenca pri učenju računanja z izrazi zmede takle primer: 5+6-3+2-7+4 "Kje moram sedaj upoštevati minus med 6 in 3? Na levi ali na desni strani?" Veliko lažje nam je, če si zgornji primer predstavljamo takole: 5+6-3+2-7+4 Vsak par računske operacije in števila, ki mu sledi, smo obarvali z enako barvo. Sedaj točno vemo, da minus med 6 in 3 pripada številu na desni strani, torej trojki. "Katera računska operacija pa pripada petici na začetku računa?" Na začetku računa ni nobene računske operacije, ima pa zato prvo število predznak (predpostavimo, da smo v množici celih števil). Predznak petice je "+", zato ga ne zapisujemo (pred števili zapisujemo le predznak "-") Predznak celega števila pa si lahko predstavljamo tudi kot računsko operacijo seštevanja:
Glede na to lahko naš račun zapišemo kot: 0+5+6-3+2-7+4 Tudi ničle na začetku računa nima smisla zapisovati, tako da je končni izgled našega računa naslednji: +5+6-3+2-7+4 V enem izmed naših prejšnjih zapisov smo omenili, da je odštevanje enako prištevanju nasprotne vrednosti oziroma vrednosti z zamenjanim predznakom ("+" v "-" in obratno). Če si predstavljamo vse enako obarvane pare v zgornjem računu kot seštevanje števil z različnimi predznaki, lahko enostavno seštejemo vsa pozitivna (5+6+2+4 = 17) in negativna (3+7 = 10) števila ter ju odštejemo med seboj, "zmaga" pa predznak "večje skupine", v našem primeru "+", saj je 17 več od 10. Množenje in deljenje Oglejmo si še en primer: 20:5⋅3 "Moram najprej deliti s 5 in nato množiti s 3?" "Moram deliti tako s 5 kot s 3?" Obarvajmo račun enako kot v prejšnjem primeru: 20:5⋅3 Sedaj vidimo, da s 5 delimo, s 3 pa množimo. Ker sta množenje in deljenje enakovredni računski operaciji, vrstni red pri tem ni pomemben. Kaj pa storimo z 20? Ker vemo, da množenje števila z 1 ne spremeni vrednosti le-tega, lahko zapišemo: (20⋅1):5⋅3 Po zakonu o zamenjavi velja tudi: (1⋅20):5⋅3 Ker so vse operacije v računu enakovredne, lahko oklepaj odstranimo: 1⋅20:5⋅3 Sedaj vidimo, da tudi z 20 množimo. Enica na začetku pa naj nas ne moti, saj ne glede na to, ali z njo množimo ali delimo, ne spremeni vrednosti člena (podobno kot prištevanje ali odštevanje ničle nekemu členu ne spremeni vrednosti izraza - glej prvi del tega zapisa). V enem izmed naših prejšnjih zapisov smo omenili, da je deljenje enako množenju z obratno vrednostjo. Če si predstavljamo vse enako obarvane pare v zgornjem računu kot množenje števil ter njihovih obratnih vrednosti, lahko enostavno zmnožimo vsa števila, ki imajo pred seboj znak množenja (20⋅3=60) ter števila, ki imajo med seboj znak deljenja (5) števila ter jih postavimo na ulomek (ulomek je enak deljenju). 60 postavimo v števec in 5 v imenovalec. Ko ulomek okrajšamo, dobimo 12. To pa je tudi rešitev našega računa. Zakon o zamenjavi (komutativnostni zakon) Zakon o zamenjavi velja le za seštevanje in množenje, za odštevanje in deljenje pa ne. Na primer:
Če odštevanje obravnavamo kot prištevanje nasprotne vrednosti odštevanca, si račun 6-3 lahko predstavljamo kot seštevanje števil +6 in -3. Ta vrstni red pa lahko zamenjamo, tako da velja:
In če na podoben način deljenje obravnavamo kot množenje z obratno vrednostjo delitelja, lahko zapišemo:
0 Comments
Zato, da namesto s štirimi osnovnimi računskimi operacijami (seštevanje, odštevanje, množenje in deljenje) računamo le z dvema (seštevanje in množenje).
Kako? Preprosto:
Zgornja razlaga je mogoče res nekoliko karikirana, je pa res, da omenjeni dve zakonitosti redno uporabljamo. Naj omenimo le nekaj primerov:
Z Evklidovim algoritmom računamo največji skupni delitelj dveh naravnih števil. No ja...to lahko storimo tudi zelo preprosto - naredimo ulomek (eno število postavimo v števec, drugo v imenovalec) in ga okrajšamo. Naredimo primer za števili 180 in 210. Ko števili okrajšamo, dobimo ulomek šest sedmin: Če ulomek želimo razširiti nazaj, moramo števec in imenovalec pomnožiti z vsemi števili, s katerimi smo ga prej krajšali. V našem primeru so to števila 2, 3 in 5, njihov zmnožek pa je 30: S tem ugotovimo, da je 30 največji skupni delitelj števil 180 in 210.
Sedaj pa isti primer izračunajmo po Evklidovem algoritmu: 210 = 180 • 1 + 30 180 = 30 • 6 + 0 Za vse tiste, ki Evklidovega algoritma (še) ne poznate ali pa ste ga pozabili:
Sedaj pa se malo "poigrajmo" z zgornjim izračunom. Drugo vrstico iz zgornjega zapisa vstavimo v prvo (+0 ne pišemo): 210 = (30 • 6) • 1 + 30 180 = 30 • 6 + 0 Po ureditvi dobimo: 210 = 30 • 6 + 30 180 = 30 • 6 V obeh vrsticah izpostavimo, kar se da izpostaviti, v spodnjem računu pa tako ali tako nimamo kaj izpostavljati: 210 = 30 • (6 + 1) = 30 • 7 180 = 30 • 6 V obeh vrsticah smo izpostavili največji skupni delitelj števil 180 in 210, ki je 30. To pa je isto število, s katerim bi krajšali ulomek 180/210 (glej prvi primer). Naredimo še en primer, tokrat z nekoliko daljšim postopkom Evklidovega algoritma. Poiščimo največji skupni delitelj števil 80 in 36. 80 = 36 • 2 + 8 36 = 8 • 4 + 4 8 = 4 • 2 + 0 Zadnjo vrstico iz zgornjega zapisa vstavimo v prvo in drugo vrstico, drugo vrstico pa v prvo (+0 ne pišemo): 80 = (8 • 4 + 4) • 2 + 4 • 2 36 = (4 • 2) • 4 + 4 Po ureditvi dobimo: 80 = 8 • 4 • 2 + 4 • 2 + 4 • 2 36 = 2 • 4 • 4 + 4 V obeh vrsticah izpostavimo, kar se da izpostaviti: 80 = 4 • (2 • 8 + 2 + 2) = 4 • 20 36 = 4 • (2 • 4 +1) = 4 • 9 V obeh vrsticah smo izpostavili 4, ki je največji skupni delitelj števil 80 in 36. To pa je isto število, s katerim bi krajšali ulomek 80/36. Kaj pa če bi uporabili kar obe varianti, malo Evklidovega algoritma in malo krajšanja ulomkov? Števili zapišimo v števec in imenovalec ulomka tako, da bo njegova vrednost večja od ena, nato pa zapis pretvorimo v celi del + ulomek. Nazadnje ulomek okrajšajmo. V prvem primeru bi račun izgledal takole: 210/180 = 1 cela in 30/180 🡺 ker ulomek lahko okrajšamo s 30 (180 = 6•30), je 30 največji skupni delitelj števil 180 in 210. V drugem primeru pa: 80/36 = 2 celi in 8/36 🡺 ker ulomek lahko okrajšamo s 4 (8 = 2•4, 36 = 4•9), je 4 največji skupni delitelj števil 36 in 80. Zaključek: Evklidov algoritem je lahko zabavna igra s številkami, ki pa je v življenju ne potrebujemo prav pogosto (niti pri matematiki :)), zato gre kaj hitro v pozabo, medtem ko je krajšanje ulomkov vedno "na tapeti" - vsaj pri matematiki :) - in ga zlepa ne pozabimo. |
ARHIV
May 2024
KATEGORIJE
All
|
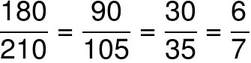
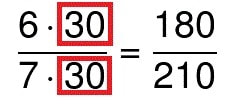
 RSS Feed
RSS Feed
