|
Pri razstavljanju izrazov moramo biti dobri opazovalci, da pravilno »identificiramo« zapis, na podlagi česar se potem odločimo za postopek. Seveda obstaja lažji način od učenja vseh kombinacij na pamet, ampak ga včasih učitelji niso veseli. Je pa z njim vseeno možno rešiti kakšno nalogo več. Omejimo se na dvočlenike, ki jih obravnavamo v osnovni šoli. Najprej je seveda potrebno vedeti, ali izraz razstavljamo ali poenostavljamo. Pri nalogi običajno jasno piše, še vedno pa je dobro »od daleč« videti, kaj bomo počeli: Poenostavljeno povedano: zgornji izraz na sliki nima oklepajev, zato ga je potrebno razstaviti, spodnji pa ima oklepaje, zato pri njem pride v poštev poenostavljanje. V nadaljevanju se posvetimo razstavljanju. Pri tem imamo v bistvu le dve večji opciji – izpostavljanje skupnega faktorja ali pa Vietovo pravilo: Oba izraza na zgornji sliki imata tri člene, ampak zgornji ima v prvem členu številski faktor, poleg tega pa ima še različne črke (spremenljivke), medtem ko gre desni po pravilu »spremenljivka na kvadrat, spremenljivka, brez spremenljivke« (govorimo o spremenljivki a na sliki). Zato prvega rešimo z izpostavljanjem skupnega faktorja, drugega pa po Vietovem pravilu. Se sprašujete, kam sta izginila kvadrat dvočlenika ter produkt vsote in razlike? Brez panike, tudi ta dva tipa razstavljanja si bomo ogledali, jima pa ne bomo dodelili svojega postopka, saj ju je moč rešiti s pomočjo vietovega pravila. V šoli vam pa tega običajno ne povedo, ampak vas naučijo še dva postopka, kot da jih že tako ali tako ni dovolj ... Najprej si oglejmo prvi »posebni primer«: Veste, kateri izraz na zgornji sliki predstavlja kvadrat dvočlenika? V bistvu vam sploh ni treba vedeti. Izraz ustreza »normam« za razstavljanje po Vietovem pravilu, torej ga ne bomo reševali z izpostavljanjem skupnega faktorja. Če bomo kot rezultat dobili dva popolnoma identična faktorja, ju bomo zapisali kot kvadrat, sicer pa enega zraven drugega. Sedaj pa si oglejmo še situacijo s produktom vsote in razlike: Če med prvi in drugi člen spodnjega izraza zapišemo »0⋅a«, se vrednost izraza ne spremeni, nova oblika pa je ustrezna za razstavljanje po Vietovem pravilu:
a² + 0⋅a – 9 Razstavljanje marsikomu povzroča kar nekaj težav, a ni potrebno, da je tako. Predvsem se ga ne smemo ustrašiti in tudi če pozabimo kakšno pravilo, imejmo v mislih, da se vedno lahko znajdemo in z nekaj logike račun rešimo nekoliko drugače.
0 Comments
Verjetno se nihče ne bi branil "nevidne sile", ki bi ga rešila vsakič, ko bi zašel v težave. Verjeli ali ne, v matematiki taka "sila" dejansko obstaja. To je število 1, ki ga v redovalnici seveda ne maramo, :) v matematičnem zvezku pa pride še kako prav.
Število 1 imenujemo tudi enota (oziroma nevtralni element) za množenje, to pa zato, ker je rezultat množenja katerega koli števila z 1 kar število samo (če koga zanima več o tem, lahko pokuka sem). Zakaj "nevidna"? Oglejmo si izraz ab. Ta izraz lahko pomnožimo z 1 tolikokrat, kot želimo, pa bo še vedno enak 1: ab⋅1 = ab⋅1⋅1 = ab⋅1⋅1⋅1 = ... = ab Ker vemo, da množenje nekega člena (če se sprašujete, kaj je to člen, lahko na hitro pokukate sem) z 1 samega člena ne spremeni, enice nima smisla pisati, dobro pa je vedeti, da je tam. :) Kateremu faktorju pripada minus? Člen -ab sestavljata dva faktorja, predznak pa nam sporoča, da je ta člen negativen. Kateremu faktorju pripada minus? Načeloma lahko pripada a-ju ali pa b-ju (saj poznate tisto: plus in minus pri množenju vrne minus ...), da se ne bomo kregali, pa lahko rečemo tudi nobenemu. :) Kako? Pomnožimo vse skupaj še z 1 in dobimo. -1ab oziroma (-1)ab. Tu pa se lepo vidi, da je minus "ukradla" enica. Ti, ti, enica :) Kako pri razstavljanju izrazov "ukalupiti" enačbo? Enačba za razliko kvadratov se glasi: a²-b² = (a+b)(a-b) Kaj pa, če imamo v izrazu recimo a²-1? Desni člen lahko mirno pomnožimo z 1 in dobimo: a²-1² To pa je že lažje, kajne? :) Podobno lahko storimo tudi z izrazom -a²+b². V enačbi je prvi člen pozitiven, drugi pa negativen, mi pa imamo ravno nasprotno situacijo. Tokrat z 1 pomnožimo kar oba člena: -1a²+1b², nato pa izpostavimo (-1): -1(a²-b²) in v oklepaju dobimo to, kar želimo. :) Ulomkov marsikdo ne mara, delno tudi zato, ker jih v izrazih ne moremo preprosto seštevati in odštevati, ampak jih moramo prej vedno razširiti na najmanjši skupni imenovalec: Nekoliko raje jih imamo v enačbah. Tu nam ulomkov ni potrebno razširjati na najmanjši skupni imenovalec, ampak z njim preprosto pomnožimo obe strani enačbe. Najboljše pri vsem tem je pa to, da gredo na ta način ulomki pa pa 😉
Linearna enačba ima običajno eno rešitev, ni pa vedno tako. Lahko se tudi zgodi, da enačba nima rešitve ali pa da je rešitev neskončno. Kako vemo, da enačba nima rešitve? Vemo, da kakršno koli množenje z 0 pomeni rezultat 0. Če pri računanju naletimo na zmnožek neznanke in števila 0, katerega rezultat ni enak 0 (na primer x • 0 = 5 ali pa recimo 0 • x = 8), je očitno, da "tu nekaj ne štima". Res je, večkratnik števila 0 mora biti vedno 0, sicer rešitev ne obstaja. Kako pa vemo, da je rešitev neskončno? Že prej smo povedali, da kakršno koli množenje z 0 pomeni rezultat 0. Če pri računanju naletimo na zmnožek neznanke in števila 0, katerega rezultat je enak 0, pa ni nič narobe. Večkratnik števila 0 je vedno 0, ne glede na to, koliko je x oziroma s katerim številom množimo 0. Zato je x lahko katero koli število, torej je rešitev karkoli oziroma ima enačba neskončno rešitev.
V matematiki se velikokrat zgodi, da nekaj dejansko je tam, a tega ne vidimo ... in - papa točka ali dve pri kontrolki :( Matematika je sinonim za urejenost, zato mora pri zapisih vse "lepo izgledati", brez "odvečne krame" in med to "kramo" spada tudi nekaj predznakov in znakov za računske operacije. Lahko pa si zadevo predstavljamo tudi drugače, zamislimo si, da so matematiki le leni in se jim teh znakov enostavno ne da pisati :) Oglejmo si nekaj najznačilnejših primerov. Znak za množenje med spremenljivkami kljub temu, da znaka za množenje med spremenljivkami (črkami v računih) ne pišemo, moramo vedeti, da je tam. A pozor: Znak za množenje med številkami je nujen! Predznak + pred prvim členom v računskem izrazu Če pred prvim členom v računskem izrazu ni predznaka, to pomeni, da je le-ta pozitiven. A pozor! Če je prvi člen negativen, moramo predznak nujno zapisati! Katerega izmed faktorjev je potrebno postaviti nad in katerega pod ulomkovo črto? Vsi številski faktorji znotraj posameznega člena imajo levo od sebe znak za množenje ali deljenje. Glede na to tudi vemo, kam jih postavimo, če člen želimo zapisati v obliki ulomka. Množenje vodi v "zgornje nadstropje" (števec), deljenje pa v "spodnje nadstropje" (imenovalec ulomka) :) Posebnost pa je faktor na skrajni levi. Tega vedno zapišemo v števec ulomka. Zakaj? Oglejmo si primer na spodnji sliki. Levo od prvega številskega faktorja si predstavljajmo še en faktor - enico, s katero pomnožimo celoten člen (vrednost člena se pri tem seveda ne spremeni, saj množenje z 1 ne spremeni rezultata). Trojka tako predse dobi znak za množenje, kar jo "pelje" v števec ulomka. Enice pa v ulomku tako ali tako ni potrebno pisati (razen če bi bila edina v števcu ali imenovalcu). Pozor! Če je pred številskim faktorjem na skrajni levi slučajno predznak + ali -, ta ne vpliva na zgoraj povedano, saj se nanaša na celoten člen. Preprosto ga prepišemo pred ulomek. Kaj se nahaja med celim delom in ulomkom? Odvisno. Če gre za števila, je vmes plus. Če pa imamo spremenljivke (črke), je vmes krat. Ničle na skrajni levi in skrajni desni strani decimalnega zapisa Ničel levo od prve števke celega dela števila in desno od zadnje neničelne decimalke (števke v decimalnem delu števila) ne pišemo: Decimalna vejica pri celem številu?
Celo število ne vsebuje decimalne vejice, je pa pri deljenju takega števila z večkratniki števila 10 dobro vedeti, "od kje pride". Vejica namreč "potrpežljivo čaka" na desni strani števke, ki v mestnovrednostnem konceptu predstavlja enico. Čeprav se čudno sliši, je to povsem običajen postopek pri obračanju enačb, ko želimo izraziti iskano spremenljivko (običajno je to x). Pri tem si velja zapomniti dve glavni pravili: Prvo pravilo: Člen, ki ga ne potrebujemo (to je tisti člen, ki ne vsebuje iskane spremenljivke), preprosto "vržemo" na drugo stran enačbe, ob tem pa mu spremenimo predznak. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Pozitiven člen na levi strani enačaja postane negativen ... ... negativni pa pozitiven: Drugo pravilo: Ko imamo na levi (ali desni) strani enačbe le še tisti člen, ki vsebuje iskano spremenljivko, le-tega "razcepimo", tako da na tej strani enačbe ostane le še iskana spremenljivka, ostale faktorje pa prestavimo na drugo stran enačbe. Ob tem se prestavljenim faktorjem ne spremeni predznak, ampak položaj. Če so bili na eni strani v imenovalcu ulomka, so na drugi strani v števcu in obratno. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Faktor, pomnožen s spremenljivko x na levi strani enačaja, se na desni strani preseli v imenovalec ulomka ... ... faktor, ki je na levi strani enačaja v imenovalcu ulomka, pa na desni strani pomnožimo s preostalim delom enačbe: Pozor! Pri drugem pravilu moramo v primeru več členov na desni strani uporabiti oklepaj!
Primer: x/2 = 2a + b x = 2(2a+b) Računski izrazi lahko vsebujejo le številke, poleg teh pa v njem lahko nastopajo tudi črke oziroma spremenljivke. Tokratni algoritem opisuje reševanje slednjih.
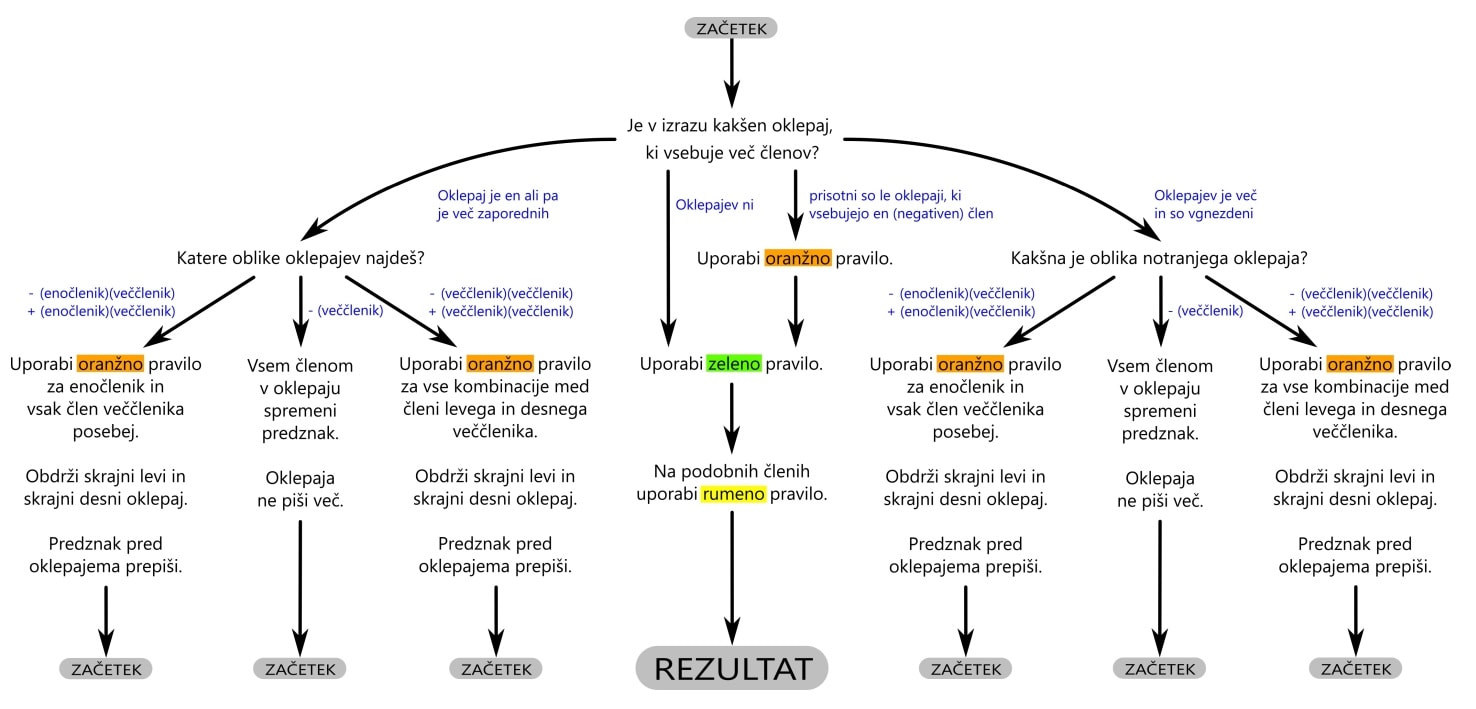
Naj na kratko razložimo naš algoritem:
* rumeno pravilo seštevanja in odštevanja, oranžno pravilo množenja in deljenja ter zeleno pravilo grupiranja podobnih členov smo definirali zato, da se v algoritmu ne ukvarjamo preveč z osnovami računanja, ampak lahko takoj preidemo na bistvo problema. Preko priloženih povezav pa seveda lahko kadarkoli ponovimo tudi osnove, če so nam slučajno "ušle iz glave" ;) Pomni! Potence veččlenikov so v osnovi množenje veččlenikov (samih s seboj), zato v algoritmu take situacije niso posebej navedene. Pomni! Če imamo le en oklepaj z več členi, pred njim pa je plus, le izbrišemo oklepaj, saj je nepotreben (tudi taka situacija v algoritmu ni posebej opisana). Pomni! Dvočleniki so v algoritmu pridruženi veččlenikom, tako da niso posebej omenjeni. V računskih izrazih poznamo dve osnovni postavitvi oklepajev:
Zaporedna oklepaja lahko razrešujemo istočasno (v isti vrstici izraza), medtem ko pri vgnezdenih oklepajih začnemo z reševanjem v notranjosti, nakar se pomikamo navzven. Primera z zaporednimi oklepaji:
Primera z vgnezdenimi oklepaji:
Za razliko od "rumenega" in "oranžnega" pravila zeleno pravilo uporabljamo samo pri računanju izrazov v algebri (črke in številke) in sicer pri poenostavljanju končnega izraza ("kače" členov, ki nam ostane potem, ko smo že razrešili oklepaje ter vse potrebno potencirali, korenili, zmnožili in delili) Pri rumenem pravilu seštevanja in odštevanja smo omenili, da v algebri podobne člene seštevamo / odštevamo ločeno ("hrušk in jabolk" seveda ne moremo seštevati :) ). Zeleno pravilo se glasi:
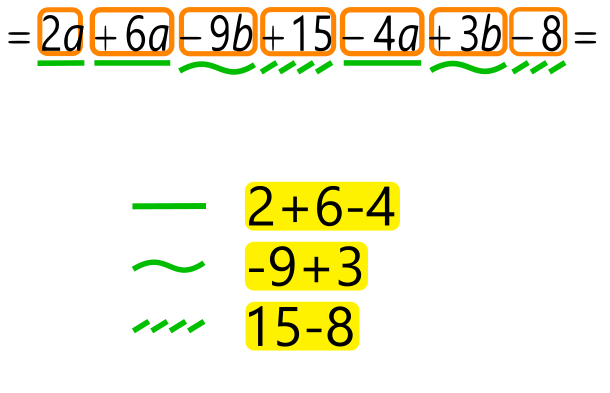
Pomni! Podobni členi so tisti členi, ki imajo različne številske faktorje in enake spremenljivke (na primer 4bc in -3bc). Enaki členi pa imajo enake tako številske faktorje kot tudi spremenljivke. Če odštejemo enaka člena, dobimo 0. Primer končne "kače" členov; členi so obkroženi z oranžno barvo in nato grupirani po zelenem pravilu. Znotraj vsake "zelene" skupine je uporabljeno rumeno pravilo; ravna črta so a-ji, vijugasta b-ji, poševno črtkana črta pa predstavlja številske člene.
Rumeno pravilo" seštevanja in odštevanja že poznamo, za naziv "mojster reševanja matematičnih izrazov" pa moramo spoznati še t.i. oranžno pravilo množenja in deljenja. Kot vemo, so seštevanje, odštevanje, množenje in deljenje osnovne matematične operacije. Vemo tudi, da imata množenje in deljenje v računskih izrazih prednost pred seštevanjem in odštevanjem. "Oranžno pravilo" bo imelo torej prednost pred "rumenim". Pravilo množenja in deljenja uporabimo pri:
Za množenje oziroma deljenje dveh členov se pravilo glasi:
Oglejmo si ga še v grafični obliki (več o pomenu krožcev si lahko ogledate v članku o računanju s simboli): Pomni! Situacijo, ko je pred oklepajem samo minus, upoštevamo kot množenje (-1) s členi v oklepaju, torej se vsem členom v oklepaju zamenja predznak! V primeru več členov pa pravilo lahko posplošimo:
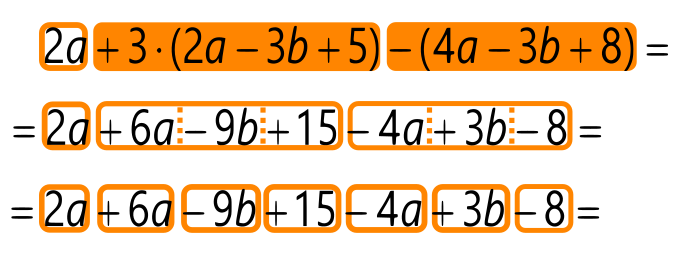
Pomni! Potenciranje števila upoštevamo kot množenje števila s samim seboj (tolikokrat, kolikor je vrednost eksponenta); v primeru potenciranja negativnega števila (minus je znotraj oklepaja, na primer (-5)²) je zato končni predznak odvisen od tega, ali je eksponent liho ali sodo število! Potenciranje posameznega števila vedno izvedemo pred množenjem z ostalimi faktorji znotraj posameznega člena! V izrazu 3⋅(-3)² recimo najprej izračunamo (-3)²=9 in nato šele 3⋅9=27. V istem koraku kot potenciranje izvedemo tudi korenjenje, a zanj oranžnega pravila ne uporabljamo. Ideja: Člen, znotraj katerega bomo uporabili oranžno pravilo, lahko obkrožimo z oranžno in ga pobarvamo. Po uporabi oranžnega pravila nastanejo novi členi, katere le obkrožimo z oranžno barvo. Z oranžno barvo lahko obkrožimo tudi ostale člene, kjer oranžnega pravila ni potrebno uporabiti. Tako dobimo pregleden "zemljevid" členov, ki jih bomo potrebovali za končen izračun po rumenem (aritmetika - samo številke) oziroma zelenem in rumenem (algebra - številke in črke) pravilu. Primer uporabe oranžnega pravila v aritmetičnem izrazu Primer uporabe oranžnega pravila v algebrskem izrazu
|
ARHIV
May 2024
KATEGORIJE
All
|









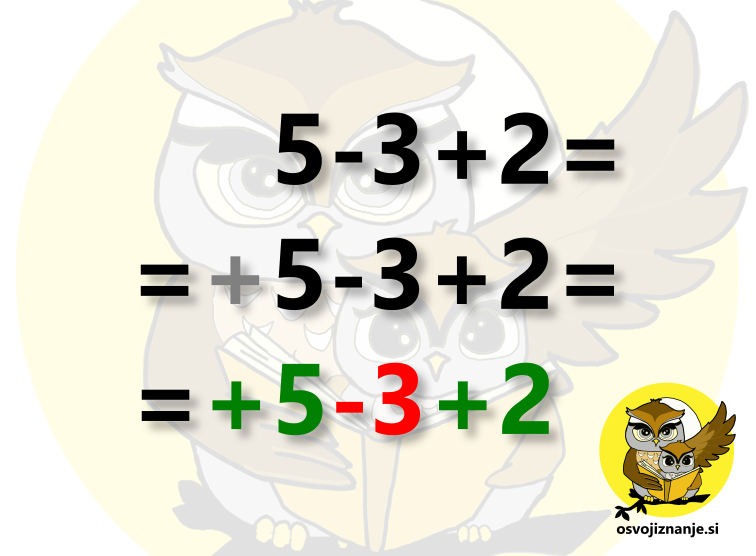

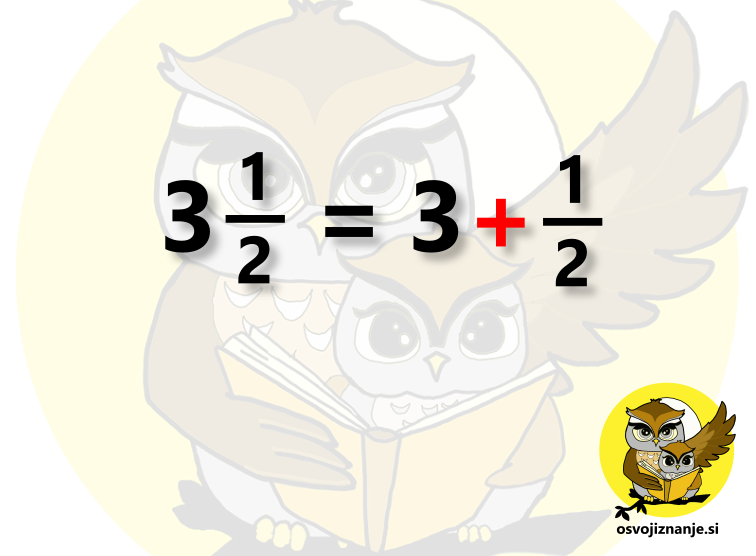
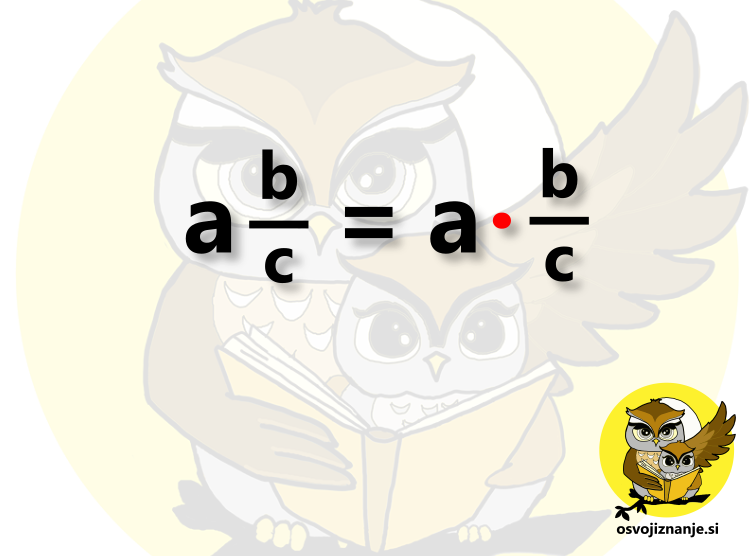



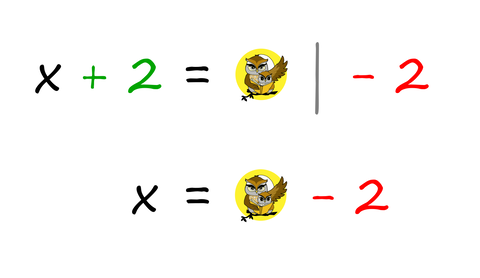
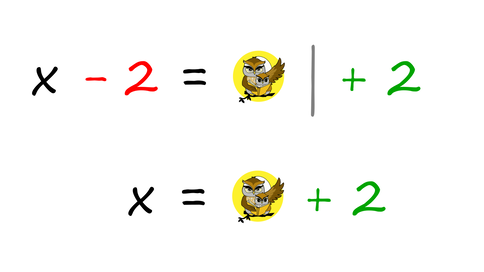
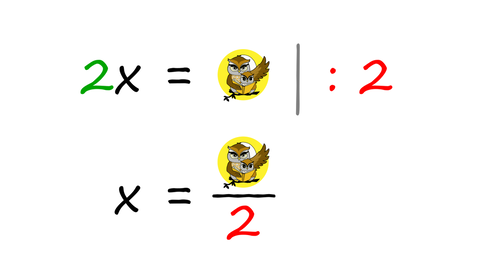
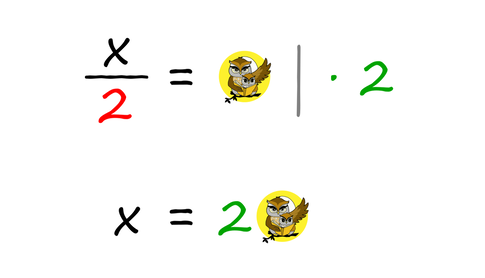

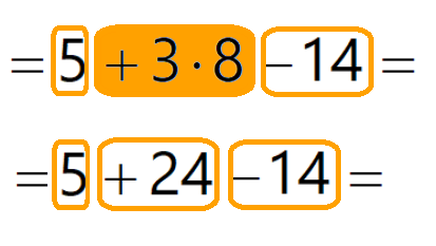
 RSS Feed
RSS Feed
