Blog Archives

Enačba za kvadrat dvočlenika v grafični obliki

16/10/2017

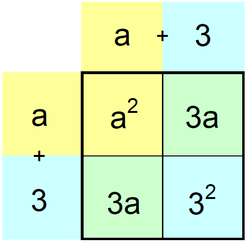
Enačba za kvadrat dvočlenika se glasi:

(a+b)² = a² + 2ab + b² oziroma
(a-b)² = a² - ab + b² oziroma
(-a+b)² = a² - ab + b² oziroma
(-a-b)² = a² + 2ab + b²

Zmeda, kajne?

Pa si zadevo poenostavimo in si enačbo predstavljajmo v grafični obliki.

Naredimo primer za (a+3)²:

Pri razumevanju zgornje slike si pomagamo tako, da si predstavljamo ploščino kvadrata, katerega stranici sta dolgi (a+3). Če seštejemo vsa polja v kvadratu, dobimo:

a²+ 3a + 3a + 3² oziroma a²+ 2(3a) + 3²

Kje stoji predznak minus, pa si zapomnimo takole:

prvi in zadnji člen na desni strani enačaja nista nista nikoli negativna, saj kvadrat katerega koli realnega števila nikoli ne more biti negativen.
predznak srednjega člena na desni določa število minusov oklepaju na levi strani enačaja. Če je to število liho, je srednji člen negativen, če pa je število minusov sodo, pa je srednji člen pozitiven.

0 Comments

Kako "sestaviti" enačbo za kub dvočlenika?

15/10/2017

0 Comments

Enačbo za kvadrat dvočlenika si nekako še zapomnimo, pri enačbi za kub dvočlenika, pa se zadeva rada ustavi.

Ponovimo:

(a+b)³ = a³ + 3a²b + 3ab² + b³ oziroma
(a-b)³ = a³ - 3a²b + 3ab² - b³ oziroma
(-a+b)³ = -a³ + 3a²b - 3ab² + b³ oziroma
(-a-b)³ = -a³ - 3a²b - 3ab² - b³

Kje je minus, si je še nekako najlažje zapomniti:

pogledamo, kateri člen v oklepaju na levi strani enačaja je negativen
vsi členi na desni strani enačaja, kjer se pojavlja negativni člen iz oklepaja na liho potenco (1 oz. 3), so negativni.

Poskusimo račun rešiti po korakih.

Najprej si nekje ob strani zapišimo:

predznaka obeh členov v oklepaju
kvadrata obeh členov v oklepaju in
kuba obeh členov v oklepaju

Nato pa gremo po vrsti:

najprej na začetku in koncu računa zapišemo kuba obeh členov v oklepaju, vmes pa pustimo kar nekaj prostora: a³ ... ... b³
nato zapišemo vmesna dve trojki, za katerima pustimo nekaj prostora: a³ 3... 3... b³
nato vstavimo predznake: a³ + 3... + 3... + b³ (od tu naprej predpostavimo, da so vsi predznaki pozitivni)
nato k prvi trojki pomnožimo kvadrat prvega člena, k drugi trojki pa prvi člen (ne na kvadrat!): a³ + 3a²... + 3a... + b³
zatem pa k prvi trojki pomnožimo še drugi člen (ne na kvadrat!), k drugi trojki pa drugi člen na kvadrat: a³ + 3a²b + 3ab² + b³

Če se še enkrat ozremo na desno stran enačbe, opazimo, da eksponent prvega člena v oklepaju pada, eksponent drugega člena pa narašča (ne pozabimo, da eksponenta 1 ne pišemo, karkoli na eksponent 0 pa je 1):

a³ + 3a²b + 3ab² + b³

0 Comments

Enačba za kvadrat dvočlenika v grafični obliki

Kako "sestaviti" enačbo za kub dvočlenika?

ARHIV

KATEGORIJE