Grafično računanje z ulomki ...

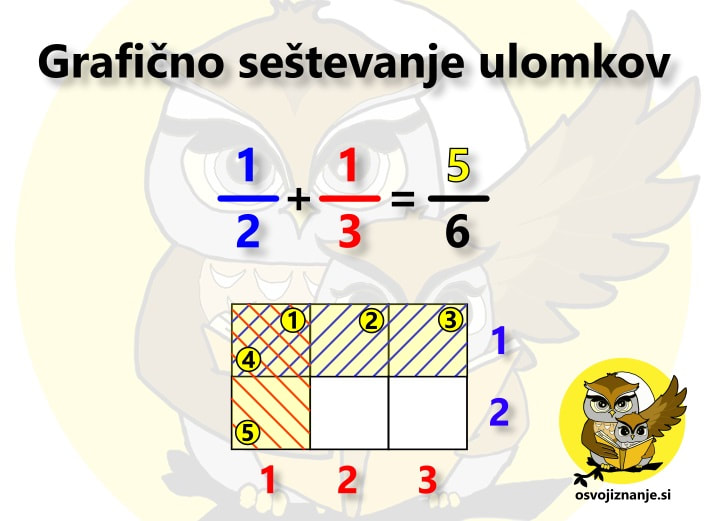
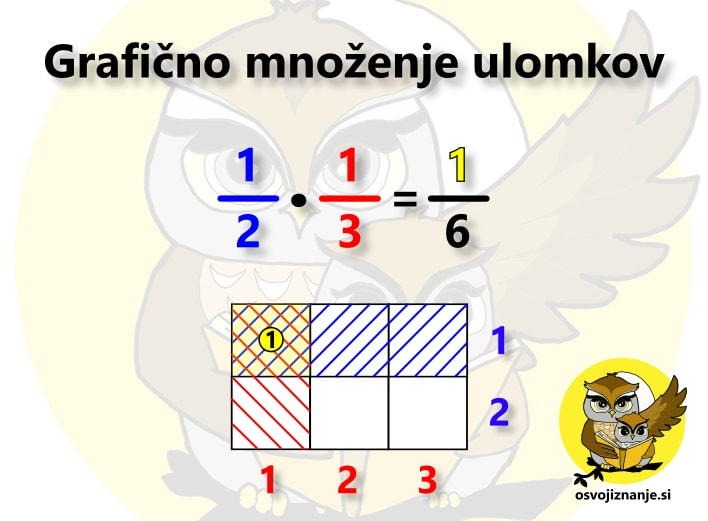
... oziroma uporaba logike pri uri aritmetike.

Pri seštevanju ulomkov »na klasičen način« vemo, da jih moramo najprej »spraviti na skupni imenovalec«, nato pa sešteti števce le-teh. Na koncu ulomek, ki predstavlja vsoto, še okrajšamo.

Kako pa bi to storili grafično?

Oglejmo si račun 1/2+1/3. Ker ulomek predstavlja del celote, eno polovico lahko predstavimo tako, da celoto razdelimo na dva enaka dela in enega pobarvamo. Z eno tretjino storimo podobno, le da celoto razdelimo na tri enake dele.

Kako pa bi naenkrat lahko predstavili oba ulomka?

Z dvodimenzionalnim poljem oziroma tabelo. S stolpci prikažemo en ulomek, z vrsticami pa drugega. V našem primeru torej potrebujemo tabelo z dvema stolpcema in tremi vrsticami (lahko storimo tudi obratno, saj za vsoto velja zakon o zamenjavi). Modra šrafura na sliki predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3.

Sedaj pa »vklopimo logiko«. V Booleovi algebri simbol »+« pomeni disjunkcijo oziroma logični »ali«. V izjavni logiki (angl. propositional logic) to povezavo označimo z znakom »∨«, v teoriji množic pa z znakom »∪«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »∥« ali zgolj angleškem izrazu »OR«.

Kaj to pomeni za našo tabelo s prikazom ulomkov?

S pomočjo uporabe logike lahko iz nje neposredno zapišemo rezultat našega računa. Ker ima tabela 6 polj, je imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Kaj pa števec? Ker imamo logično relacijo »ali«, moramo prešteti vsa polja, ki so šrafirana ali modro ali rdeče. Eno polje je šrafirano z dvema barvama, torej ga moramo šteti dvakrat. Imamo torej eno modro, dve rdeči in eno dvobarvno šrafirano polje, skupaj torej 1+2+2 oziroma 5 polj. Števec je torej 5, kar pomeni, da je vsota enaka 5/6.

Pri množenju ulomkov »na klasičen način« pa zmnožimo tako števce kot imenovalce ter okrajšamo, »kar se da«.

Za primer uporabimo ista ulomka, le da ju tokrat zmnožimo. Iščemo torej produkt 1/2 · 1/3. Ulomka predstavimo na povsem enak način kot pri seštevanju, le rezultat bomo prebrali drugače. Zopet imamo torej tabelo z 2 stolpcema in 3 vrsticami, kjer modra šrafura predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3.

Ponovno »vklopimo logiko«. V Booleovi algebri simbol »*« pomeni konjunkcijo oziroma logični »in (hkrati)«. V izjavni logiki to povezavo označimo z znakom »∧«, v teoriji množic pa z znakom »∩«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »&« ali zgolj angleškem izrazu »AND«.

S pomočjo naše tabele zapišimo še rezulat. Ker ima tabela 6 polj, je tudi tu imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Pri števcu pa bo nekoliko drugače. Ker imamo logično relacijo »in hkrati«, moramo prešteti vsa polja, ki so šrafirana tako modro kot rdeče. Tako je le eno polje, kar pomeni, da je števec enak 1. Zmnožek ulomkov 1/2 in 1/3 je torej enak 1/6.

Omenjena metoda je mogoče nekoliko daljša od »klasične«, saj je tu in tam potrebno kakšen rezultat še dodatno okrajšati, nam pa omogoča zelo dober vpogled v koncept računanja z ulomki, česar nam »piflarski« postopki ne nudijo.

Ste pogrešili odštevanje in deljenje? Odštevanje je »pokrito« s prištevanjem nasprotne vrednosti, deljenje pa z množenjem z obratno vrednostjo.

Na koncu pa še vprašanje za vas. Kako bi grafično predstavili vsoto oziroma zmnožek treh ulomkov?