Jih znate našteti? ;) Še enkrat jih ponovimo posebej za vas:

• eksplicitna
• implicitna
• odsekovna

Marsikdo je že zamešal vsaj prvi dve obliki (obe imeni izgledata enako neprivlačno :)), tretja je pa sploh "krneki", čeprav - moramo priznati - to niti ni. Pa pojdimo lepo po vrsti.

Eksplicitna oblika zapisa enačbe premice

Najprej razrešimo dilemo med eksplicitnim in implicitnim zapisom. Besedi seveda izvirata iz latinščine, v oči oziroma ušesa pa nas najbolj zbode predpona pri prvi, to je "eks-", ki po latinsko pomeni "izven" oziroma "iz".

Kdo je v tem primeru "zunaj"? Odvisna spremenljivka y. Na drugo stran enačaja jo je namreč postavila neodvisna spremenljivka x v družbi koeficientov (številk). 

To je nekako tako, kot da bi "eks" dekle pred vrata postavilo "eks" fanta. Auč, not good.

​Na sliki imate primer eksplicitnega zapisa:

Odsekovna oblika zapisa enačbe premice

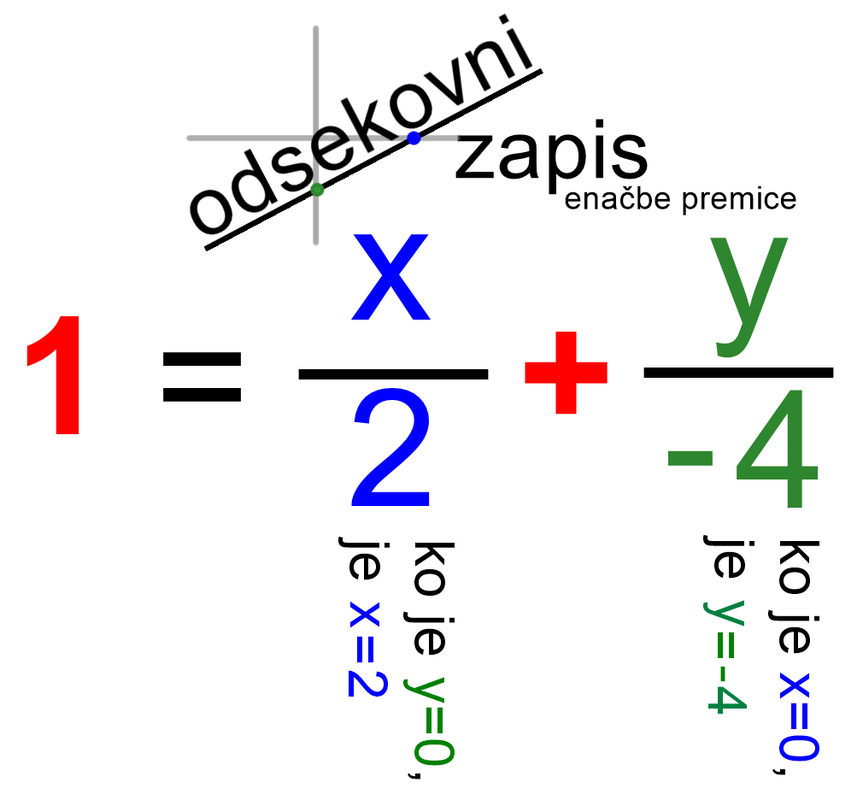
Ta zapis je po eni strani najbolj zakompliciran, po drugi strani pa si ga je najlažje predstavljati, saj je v neposredni povezavi z grafom funkcije.

Tokrat je na svoji strani enačbe "osamljena" enica. Kaj nam ta enica pove?

• Če je x enak 0, je vrednost prvega ulomka na desni strani enačbe enaka 0 in števec v drugem ulomku mora biti enak imenovalcu, da bo njun količnik 1 z leve strani enačbe. Omenjena situacija predstavlja presečišče z ordinatno (y) osjo oziroma točko (0,-4) iz našega primera
• Če pa je y enak 0, je vrednost drugega ulomka na desni strani enačbe enaka 0 in števec v prvem ulomku mora biti enak imenovalcu, da bo njun količnik 1 z leve strani enačbe. Omenjena situacija predstavlja presečišče z abscisno (x) osjo oziroma točko (2,0) iz našega primera:

Enkrat je bilo v enem razredu ene šole eno dekle. In rada se je oblačila čisto "po svoje". Ker je bilo njenim sošolkam njeno oblačenje všeč, so jo pri tem posnemale.

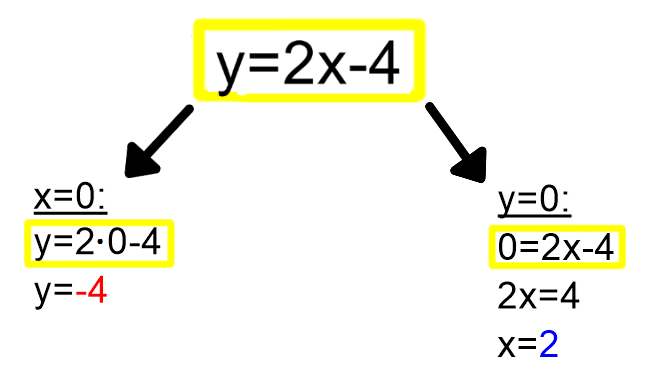
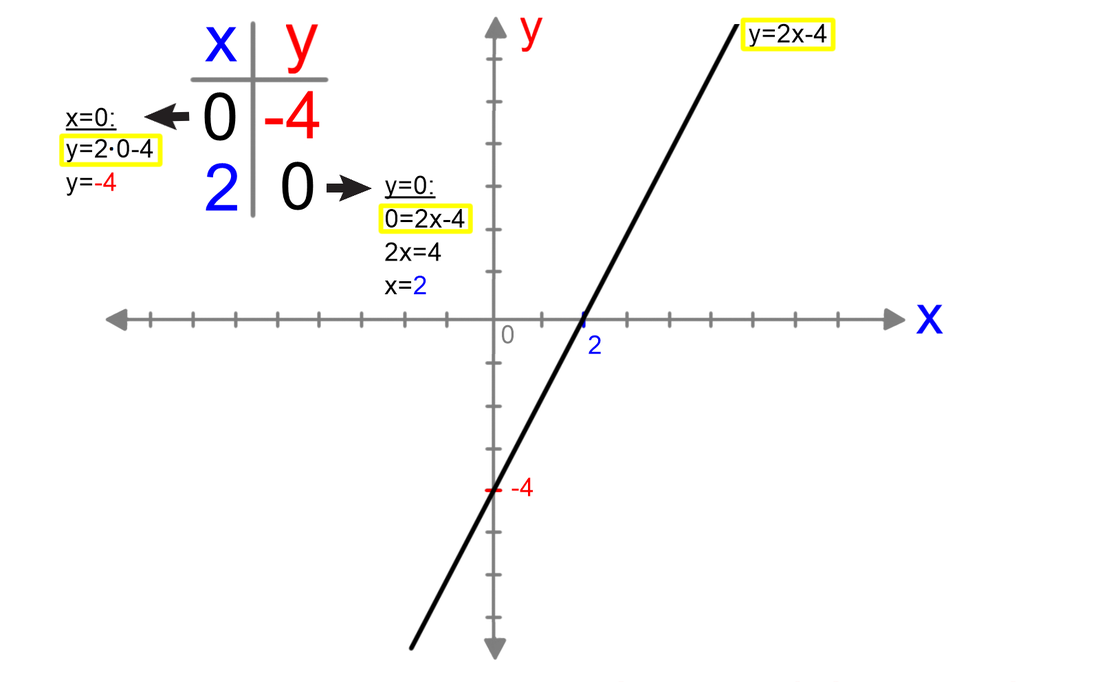
In kje je tu matematika? 

​Dekle, ki se je oblačilo "po svoje", lahko označimo kot neodvisno, medtem ko so posnemovalke od nje odvisne.

Resno, kje je tu matematika?

Tako kot v zgornji zgodbi imamo tudi pri matematiki spremenljivke, ki so lahko odvisne ali pa neodvisne. Odvisne so seveda odvisne od - neodvisnih :) Odvisno spremenljivko običajno označimo z y, neodvisno pa z x. Na primer: y=2x+4.

No, sedaj pa imate matematiko :)

Načinov za risanje grafov linearnih funkcij je več; z enimi pokažete več znanja (ki ga tudi hitro pozabite), drugi so pa bolj enostavni, a jih zlepa ne pozabite. Pobliže poglejmo enega od slednjih.

Narišimo graf linearne funkcije y=2x+4. Vemo, da ima linearna funkcija dve spremenljivki. Ena je neodvisna (x), druga pa je odvisna (y). Vse, kar morate storiti je, da vsako od njiju izenačite z nič in preverite, kakšno vrednost ima pri tem druga spremenljivka:

S tem, ko smo vrednost spremenljivk x in y postavili na 0, smo dobili dve točki na koordinatnem sistemu. Ker imata vsaka eno od koordinat enako 0, ležita vsaka na eni od koordinatnih osi in ju je zato lahko označiti. Skoznji potegnemo le še premico in že imamo graf linearne funkcije.

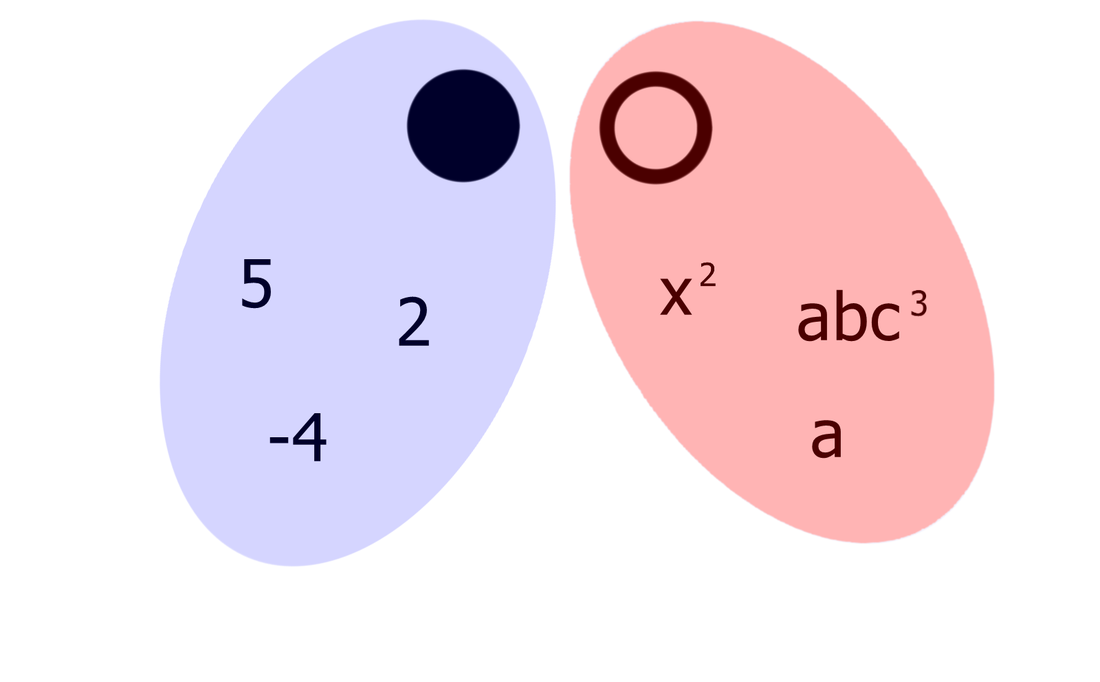
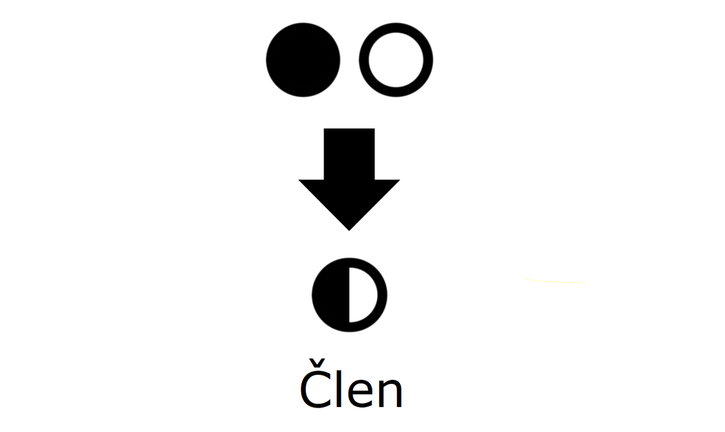
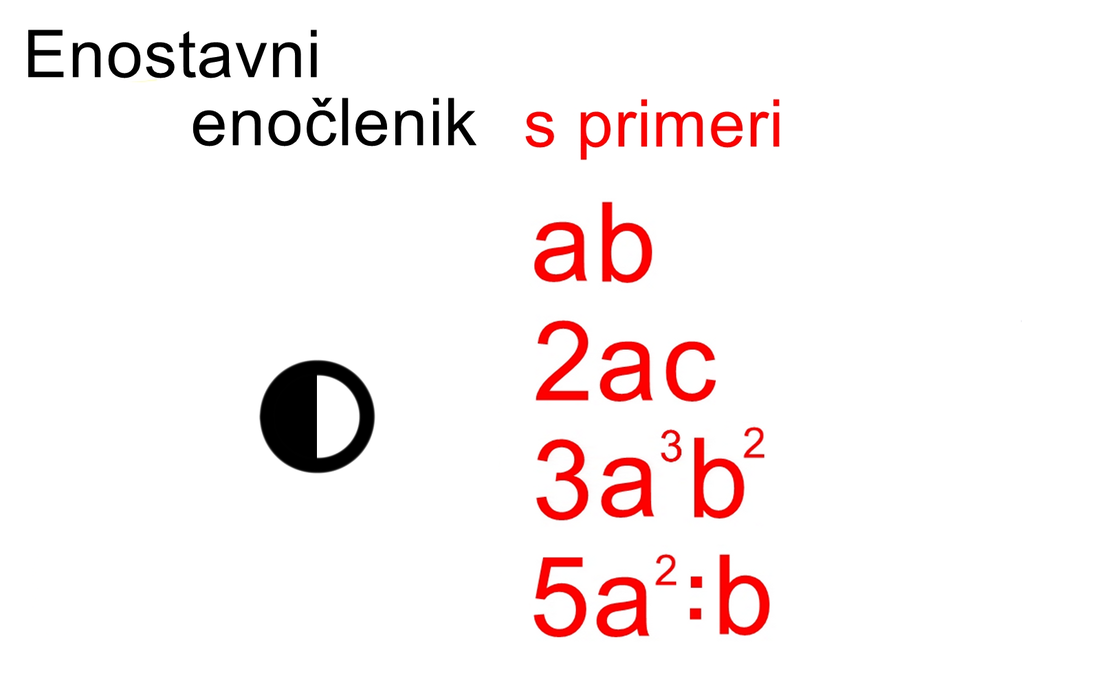
Izrazi, enačbe, neenačbe, poenostavljanje, razstavljanje... Nočna mora za tistega, ki ne razume, "šala-mala" za tistega, ki "se mu posveti". 

Skozi nepregledno množico pravil se bomo tokrat skušali prebiti s pomočjo simbolov, kar bo všeč predvsem tistim, ki ste bolj "vizualni tip".

Ponovitev

Najprej ponovimo pojem "člen".  Poenostavljeno rečeno je člen skupek številk in črk, med katerimi lahko nastopajo še simboli za množenje in deljenje ter eksponenti potenc in koreni. 

Ne pozabimo: znotraj člena simboli za seštevanje in odštevanje ter predznaka + in - ne nastopajo, razen če niso "ujeti" med oklepaje. So pa s simboli za seštevanje in odštevanje členi povezani med seboj!

Definicija simbolov

Začnimo z enočlenikom. Označimo ga z dvema krogoma:

• poln krog (predstavlja številko oziroma koeficient - številski faktor),
• prazen krog  (predstavlja črko oziroma spremenljivko).

Med njima je znak za množenje, ki pa ga ne pišemo. Pod njima je na sliki še nekaj primerov:

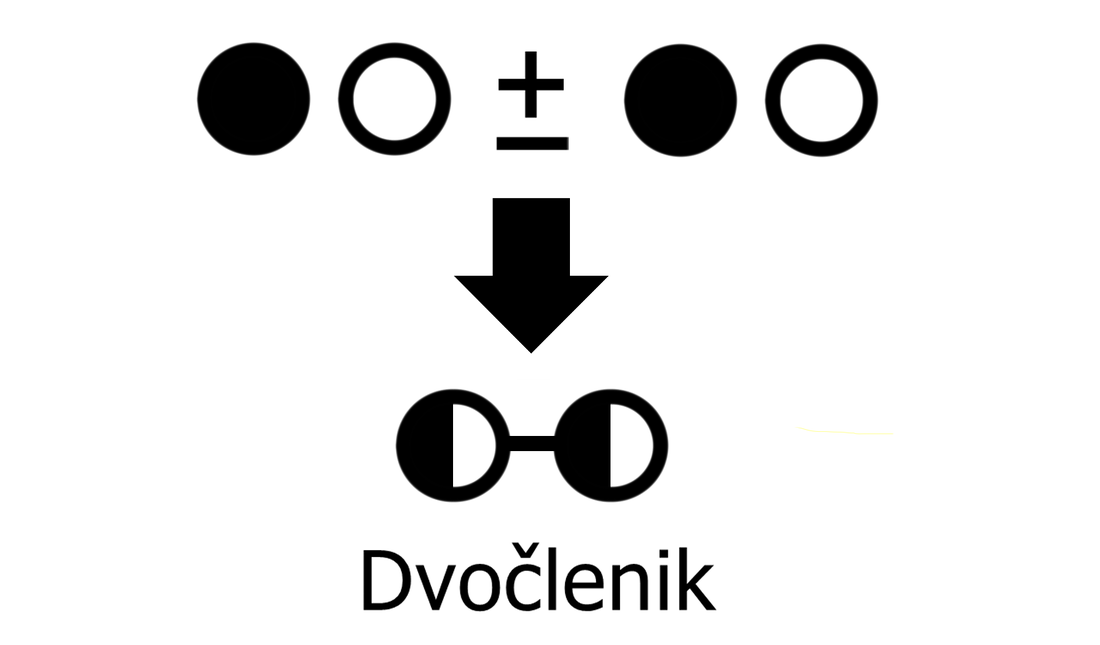
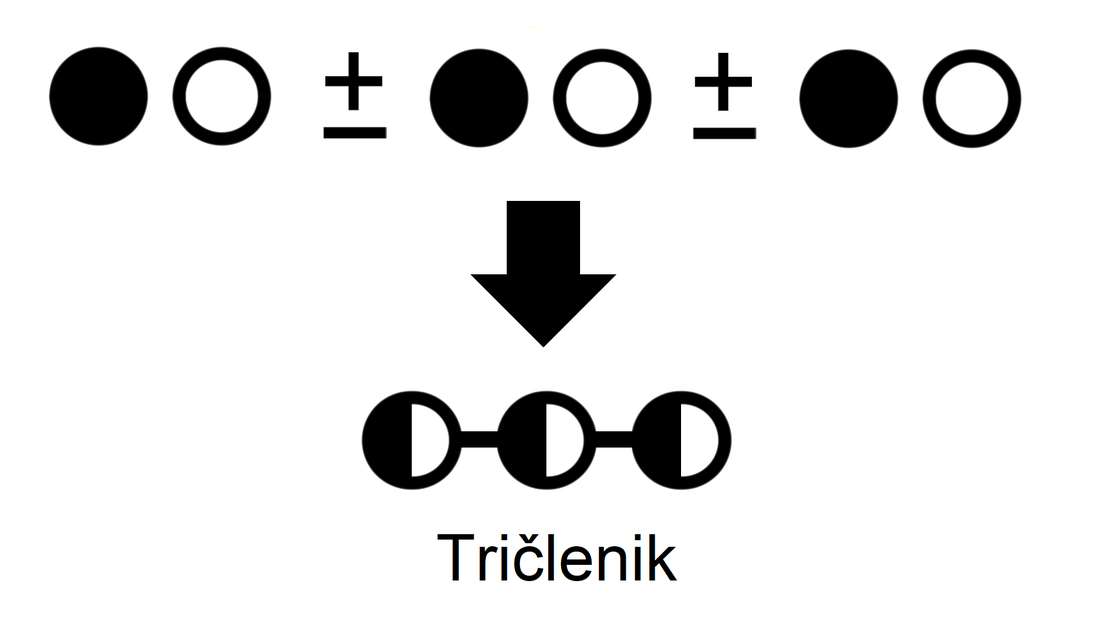
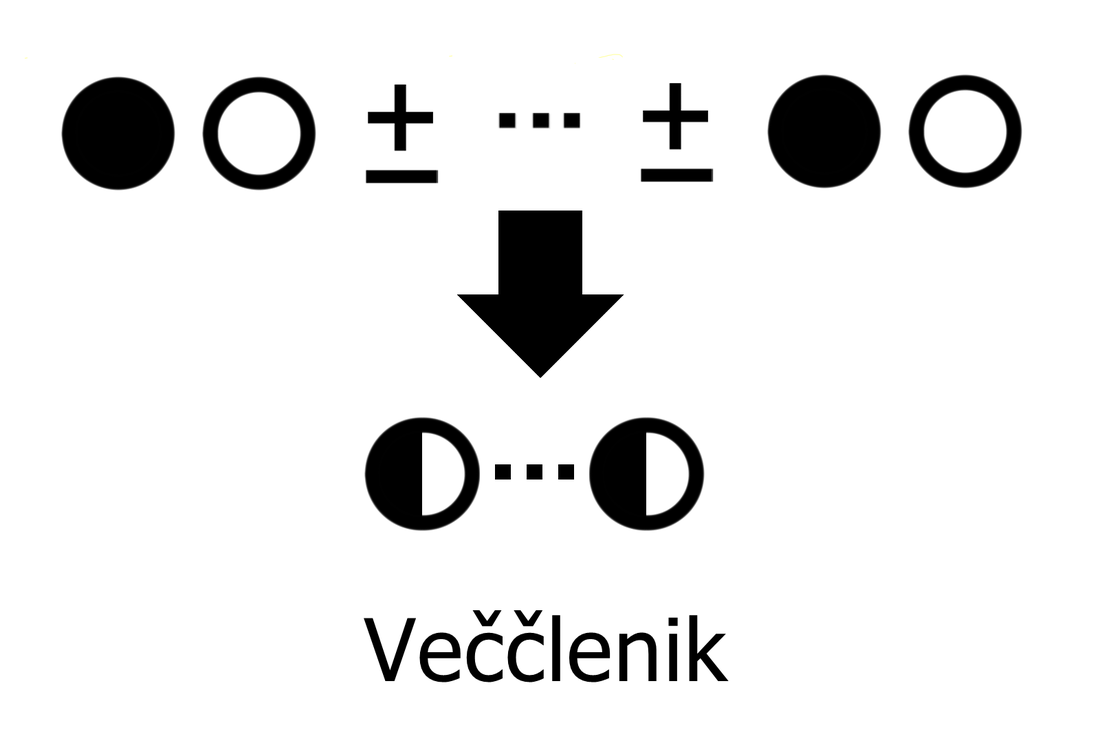
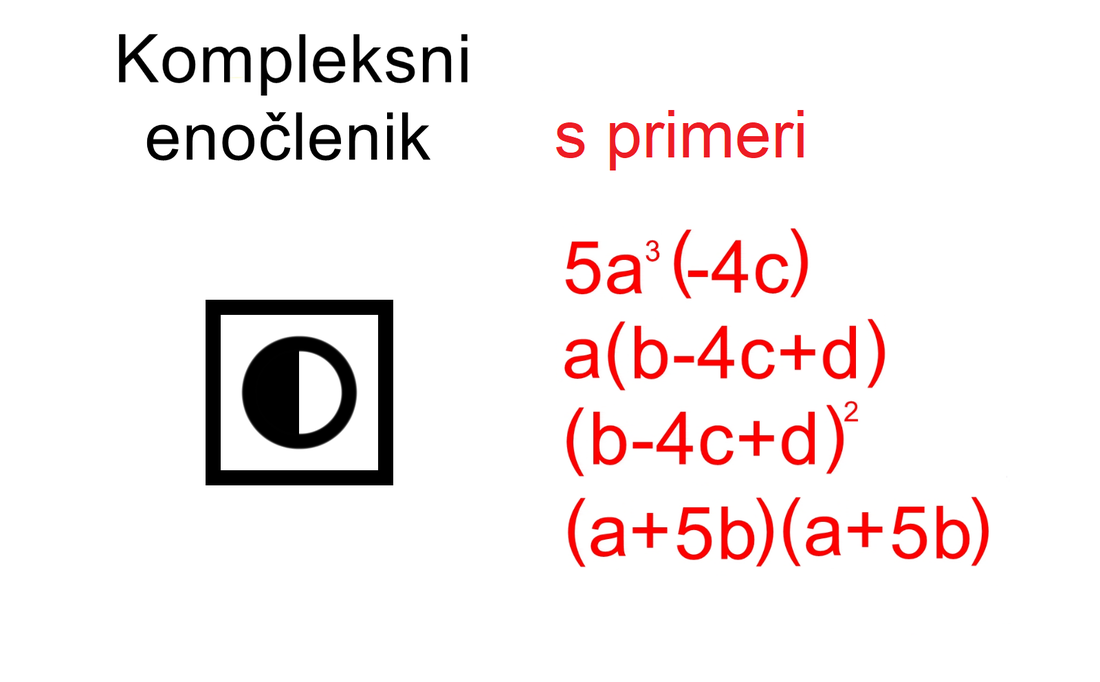
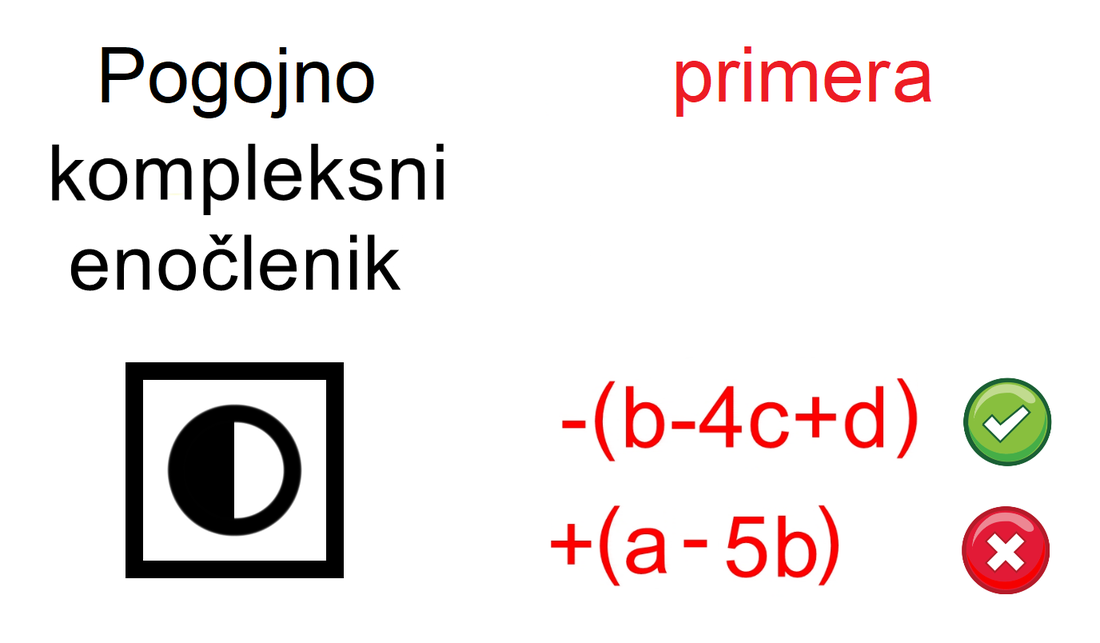
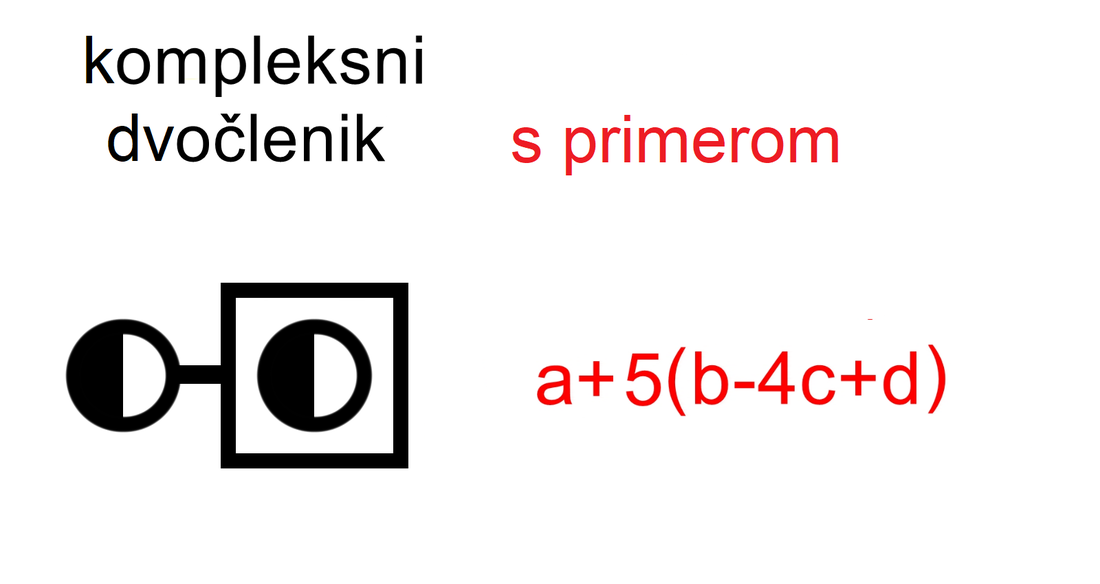
Če enočlenik ne vsebuje spremenljivke (take izraze srečamo v aritmetiki - samo številke, brez črk), rišemo le poln krog.

Za boljšo preglednost lahko kombinacijo polnega in praznega kroga poenostavimo:

Če med dva člena zapišemo + ali -, dobimo dvočlenik. Mi ga bomo označili takole:

V izrazih se pogosto pojavlja tudi tričlenik:

Ker je število členov lahko poljubno, dodajmo še simbol za veččlenik:

Enočlenika običajno ne predstavljata le koeficient in spremenljivka (številka in črka, na primer 5a), ampak je sestavljen iz več delov, pogosto z oklepaji (na primer a(b-c)(d+e)). Tak enočlenik bomo poimenovali "kompleksni enočlenik".

Seznam vseh simbolov je na naslednji sliki:

Oglejmo si nekaj primerov za enostavni in kompleksni enočlenik:

Če imamo le en oklepaj in pred njim stoji minus, je enočlenik pogojno kompleksni, saj gre v tem primeru za množenje oklepaja s številskim koeficientom -1 (posledično se po odpravi oklepaja vsem členom v oklepaju spremeni predznak):

- (b-4c+d) = (-1)·(b-4c+d) = -b+4c-d

Če pa pred oklepajem stoji plus, enočlenik ni kompleksen, saj oklepaj v tem primeru sploh ni potreben:

+ (a-5b) = a-5b

Če enostavni in kompleksni enočlenik združimo v dvočlenik, dobimo:

Zapis računskih pravil s simboli

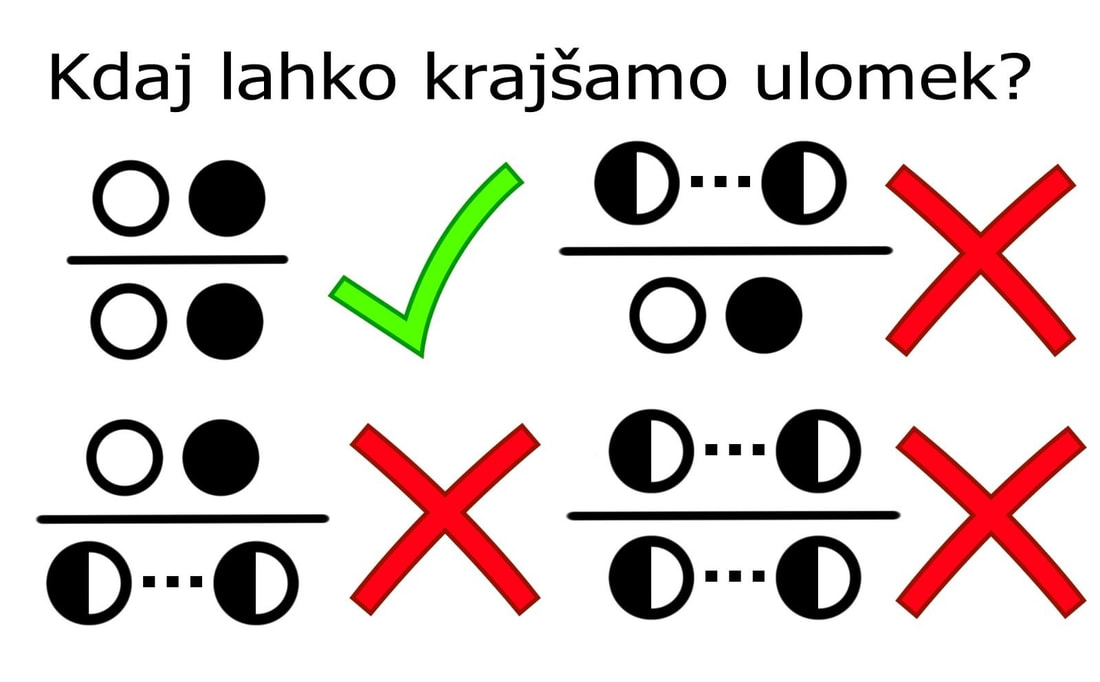
Za primer si oglejmo zapis pravila za krajšanje ulomkov.

Ulomek lahko krajšamo samo takrat, kadar je tako v števcu kot v imenovalcu enočlenik. Kadar imamo opravka z veččleniki, jih je potrebno najprej razstaviti: