|
Za vas smo pripravili "univerzalno" orodje, s katerim boste lahko kjerkoli in kadarkoli narisali graf racionalne funkcije ter reševali naloge s polinomi in racionalnimi funkcijami. Prvi se od slednjih razlikujejo predvsem po tem, da nimajo polov, s čimer so tudi njihovi grafi "lepši" :) Dobra novica pa je tudi ta, da si boste po branju tega prispevka omenjeni pripomoček lahko pripravili čisto sami :) Da bo pripomoček res univerzalen, ga pripravimo kar za racionalno funkcijo (za polinome ga bomo pa na koncu poenostavili). Naloge opisanega tipa običajno zahtevajo graf funkcije ali zapis rešitve neenačbe. Rešitev neenačbe je preprosto interval (pozor: na x osi!), kjer se graf nahaja nad ali pod določeno mejo. Predpostavimo, da ima naša racionalna funkcija dve ničli:
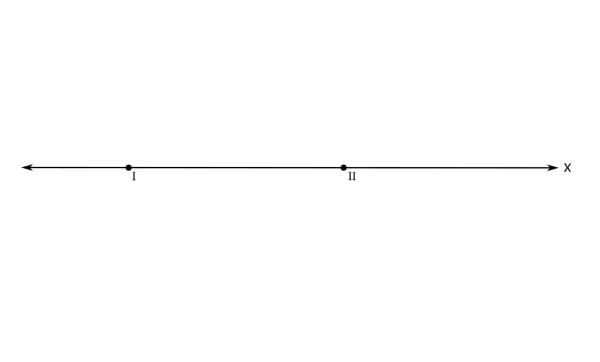
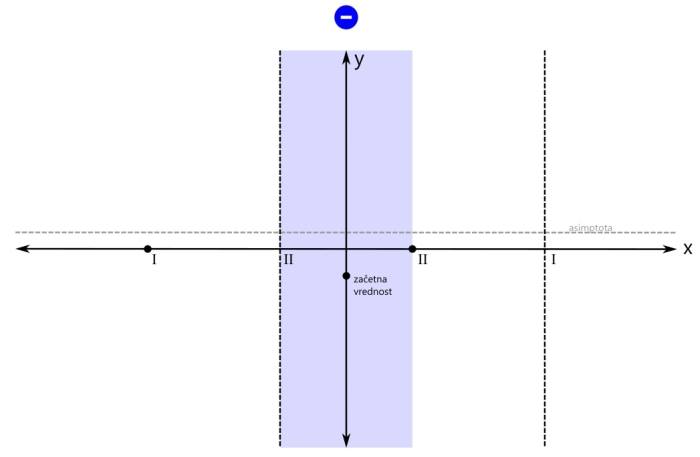
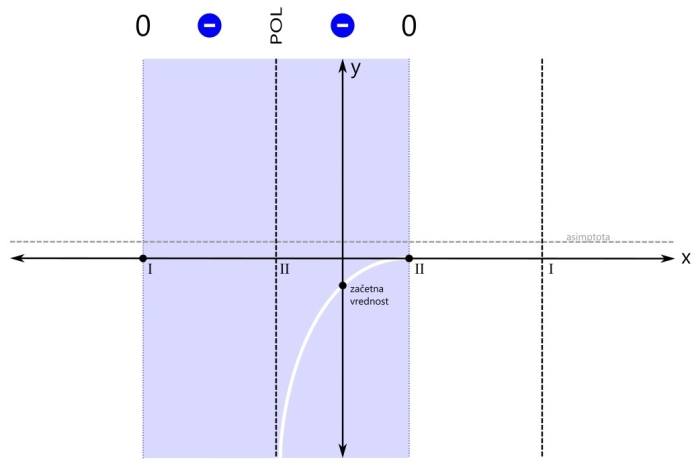
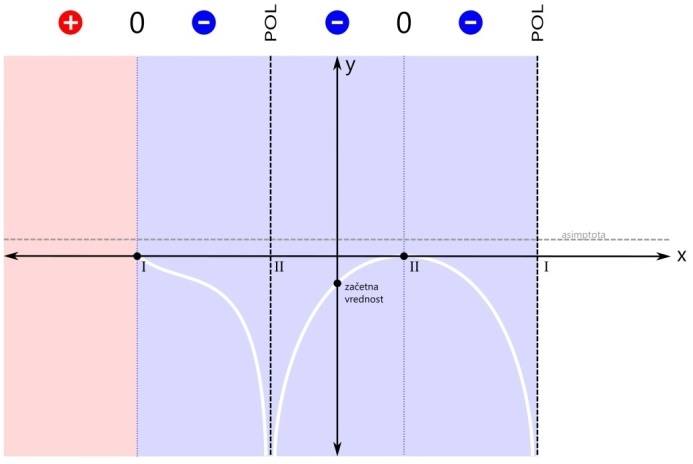
Računsko do teh ničel pridemo tako, da polinom v števcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=-3 in x₂=x₃=1. Narišimo x os in na njej označimo ničli (s pikama). Ničlo prve stopnje označimo z rimsko 1, ničlo druge stopnje pa z rimsko 2: Naša racionalna funkcija naj ima tudi dva pola:
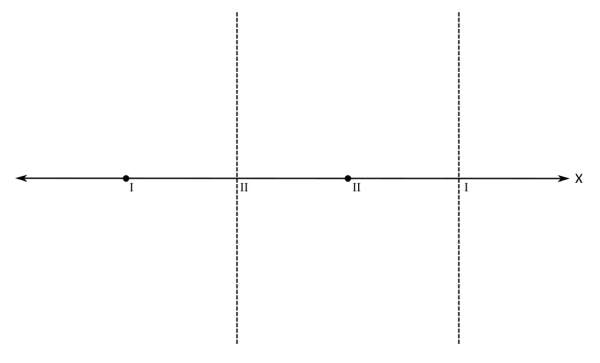
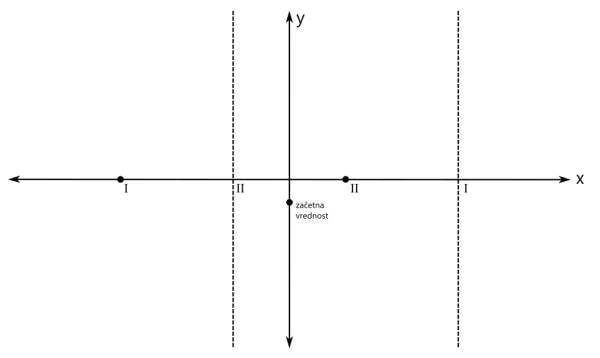
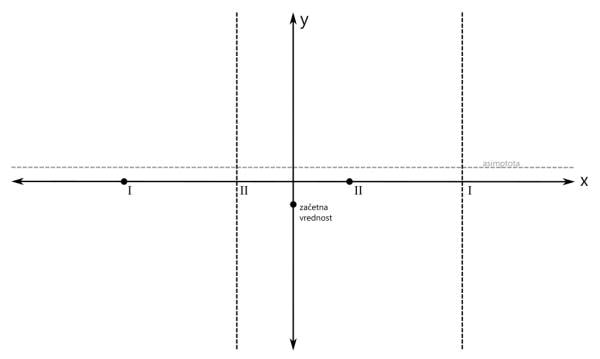
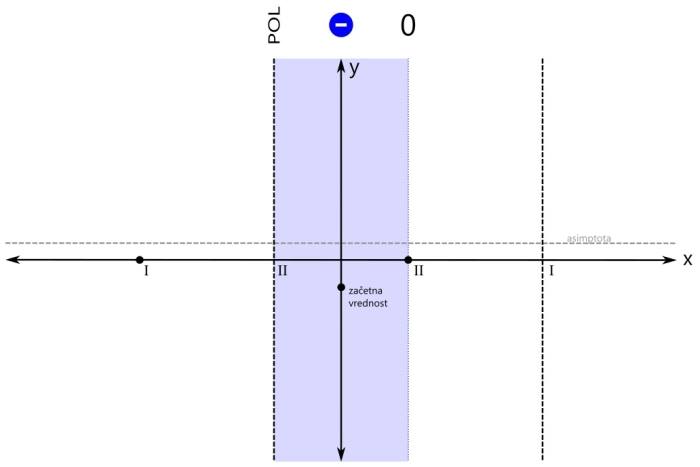
Računsko do teh polov pridemo tako, da polinom v imenovalcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Z drugimi besedami, poiščemo ničle polinoma v imenovalcu. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=x₂=-1 in x₃=3. Ampak pozor! Kljub temu, da govorimo o ničlah, so na grafu to poli, saj gre za polinom v imenovalcu! Na x osi označimo še pola (z navpičnima črtkanima črtama). Pol prve stopnje označimo z rimsko 1, pol druge stopnje pa z rimsko 2: Ničle in pole naše racionalne funkcije smo označili, sedaj je na vrsti začetna vrednost. V našem primeru je začetna vrednost negativna. Pozor! Za razliko od vrednosti ničel in polov, ki sta bili vrednosti x, je začetna vrednost vrednost y! Na primer y=-0,5. Računsko do začetne vrednosti pridemo tako, da vse x v zapisu racionalne funkcije nadomestimo z 0 in izračunamo vrednost funkcije. Z drugimi besedami, začetna vrednost je količnik prostih členov polinomov v števcu in imenovalcu. Pozor! V primerih, ko se v x=0 nahaja kakšna ničla ali pol, je potrebno izbrati novo začetno vrednost, na primer pri x=-1 ali x=1. Narišimo še y os in na njej označimo začetno vrednost: Označimo še vrednost, ki jo naša funkcija doseže pri zelo majhnih oziroma velikih vrednostih x (po domače rečeno "levo oz. desno v neskončnosti", čeprav neskončnosti dejansko ne moremo doseči). To vrednost v koordinatnem sistemu predstavlja premica (lahko je tudi krivulja, a to spada že med zahtevnejšo matematiko), ki jo graf funkcije doseže na skrajni levi oz. desni strani (v "neskončnosti"). To premico imenujemo asimptota. Le-ta je lahko vodoravna (vodoravna asimptota) ali pa poševna (poševna asimptota). Pozor! Tako kot pri začetni vrednosti nas tudi pri asimptoti zanima vrednost y! Računsko do asimptote pridemo tako, da najprej preverimo stopnji polinomov v števcu in imenovalcu racionalne funkcije (to sta najvišja eksponenta x, ki se pojavita - pri potenci x², gre recimo za polinom 2. stopnje):
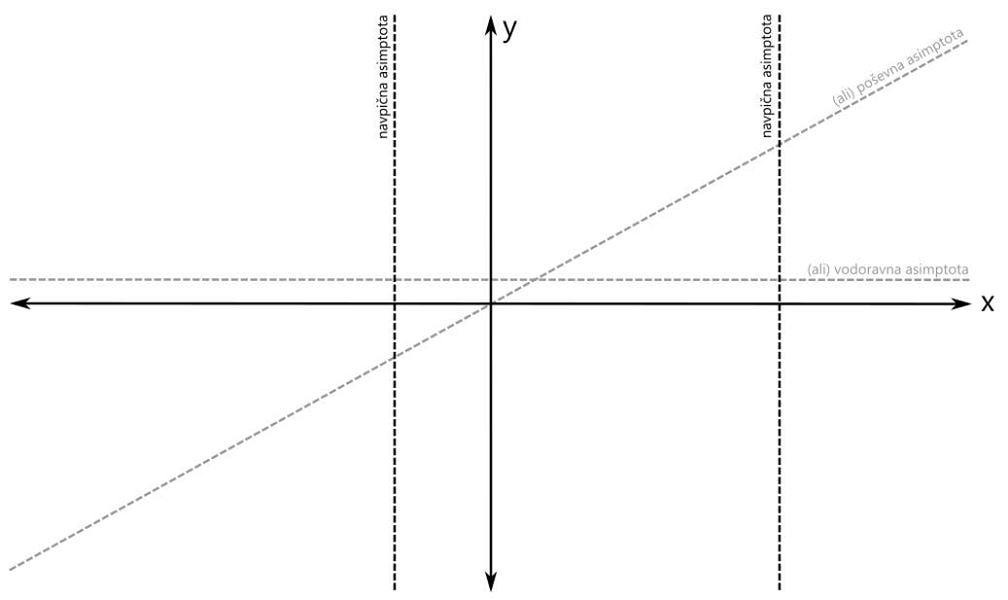
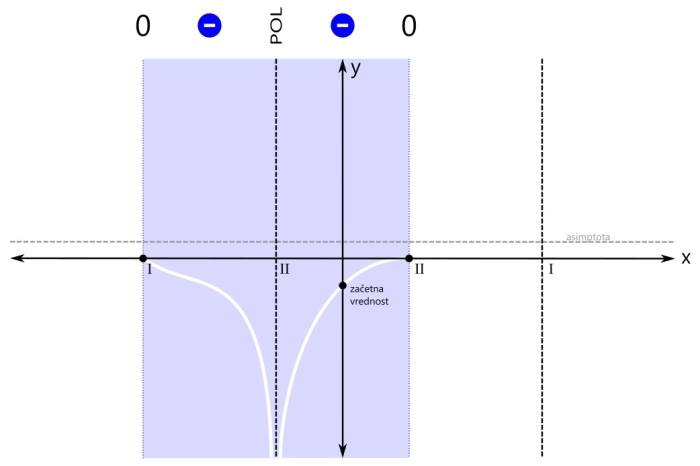
Pozor! Pri asimptoti je pomembno tudi to, da jo graf pri majhnih vrednostih x lahko seka, kar za pol recimo ne moremo reči. V našem primeru imamo vodoravno asimptoto, njena vrednost je pa večja od nič: Ustavimo se še nekoliko pri asimptotah. Po definiciji je asimptota premica ali krivulja, ki se v neskončnosti približuje drugi krivulji, ne da bi jo dosegla. Omenili smo vodoravno in poševno asimptoto. Ti dve asimptoti se nanašata na obnašanje grafa racionalne funkcije skrajno levo oziroma desno (-∞ oz. +∞ na x osi). Vodoravna in poševna asimptota hkrati ne moreta obstajati, saj se graf v neskončnosti lahko približuje le eni od njiju. Ne pozabimo: Vrednost vodoravne oz. poševne asimptote zapišemo kot y=... Pri risanju racionalne funkcije pa se skoraj vedno (kadar ima funkcija vsaj en realni pol) srečamo s še eno asimptoto, to je navpična asimptota. Ta je vedno navpična in poteka skozi pol racionalne funkcije. Navpične asimptote se nanašajo na obnašanje grafa racionalne funkcije v okolici polov (poli se nahajajo na x osi, graf pa gre v njihovi bližini navzgor ali navzdol proti neskončnosti). Navpičnih asimptot je za razliko od vodoravne in poševne lahko več - toliko, kolikor ima racionalna funkcija različnih realnih polov. Ne pozabimo: Vrednost navpične asimptote zapišemo kot x=... Navpičnih asimptot pri risanju grafa racionalne funkcije običajno ne omenjamo, le preprosto rečemo, da smo na koordinatnem sistemu označili pol racionalne funkcije. Je pa dobro, da vemo, da gre tudi v tem primeru za asimptoto. Vse asimptote rišemo kot črtkane premice. Tako, glavne značilne točke grafa imamo (stacionarne točke bomo izpustili), sedaj pa pričnimo z risanjem grafa. Graf bomo risali po odsekih, pred tem pa bomo na vsakem odseku določili predznak funkcije. Začnimo z odsekom okoli začetne vrednosti. Začetna vrednost je v našem primeru negativna, zato bo negativno tudi področje okoli nje. Za začetek z modro obarvajmo področje do prvega pola oz. ničle na levi oz. desni strani: Preverimo še predznak funkcije na robovih narisanega območja, označenega z modro barvo:
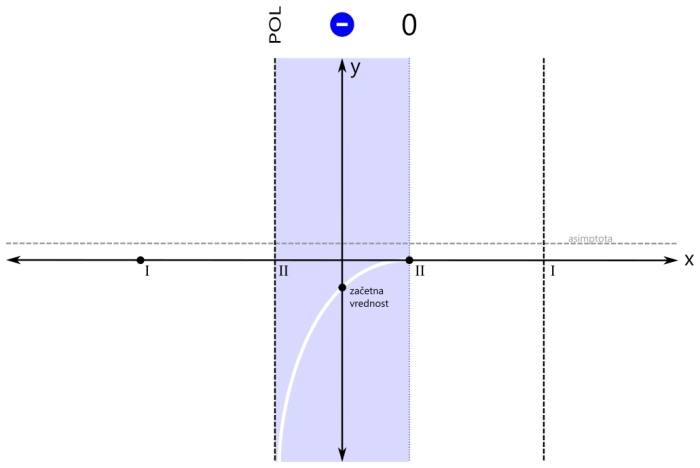
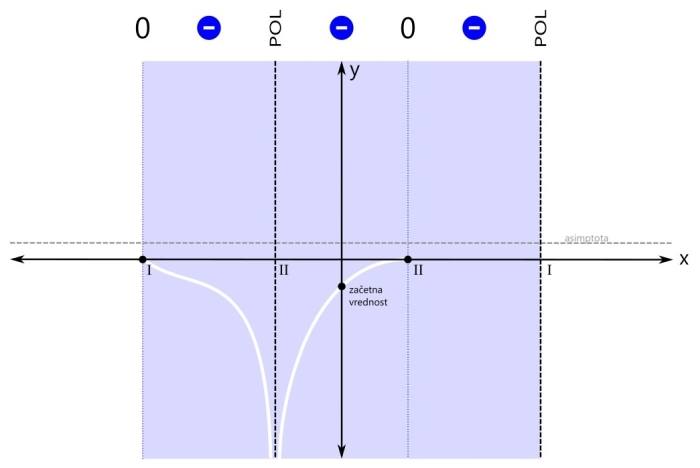
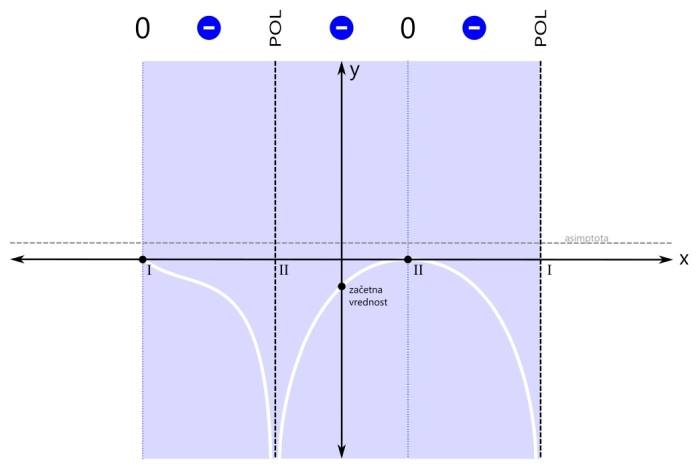
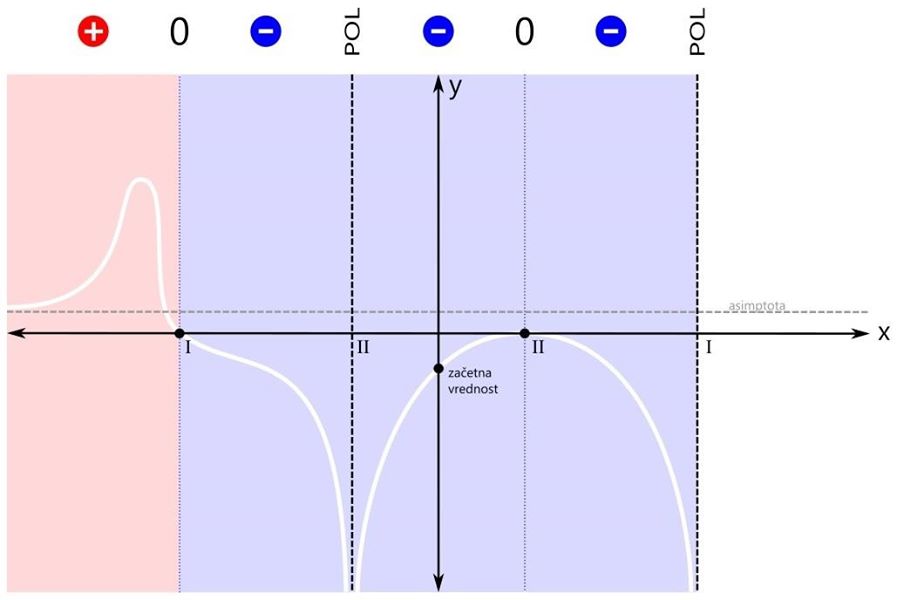
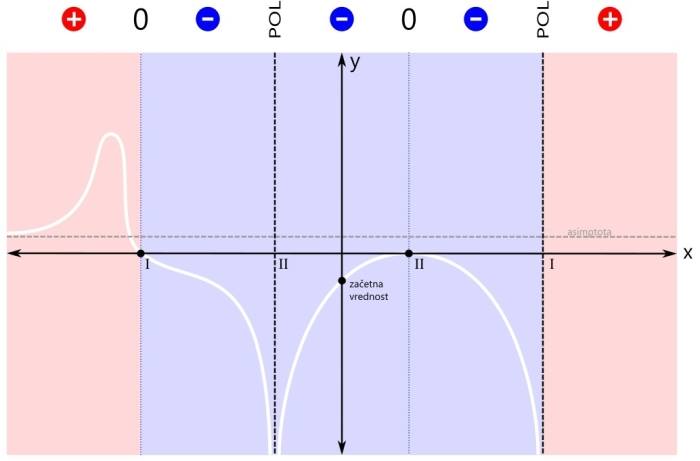
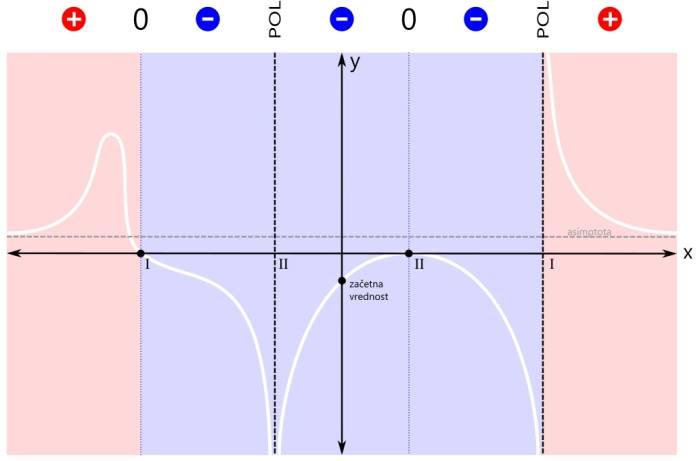
Sedaj pa pričnimo z risanjem grafa. Risali ga sproti z barvanjem območij predznaka funkcije. Zaenkrat imamo eno območje (modro). Začnimo pri začetni vrednosti. Pojdimo najprej v levo stran (do meje obarvanega območja). Ker se tam nahaja pol, graf zavije navzdol proti neskončnosti. Pozor! Navzgor graf ne more, saj bi pri tem sekal abscisno os, to pa drugje razen pri ničli ni dovoljeno! Na desni strani obarvanega območja pa imamo ničlo, zato začetno vrednost preprosto povežemo z ničlo na njeni desni. Pozor! Črta naj ne bo ravna, saj nimamo linearne funkcije! Pri risanju se izogibajmo še ostrim zavojem, pa smo že na dobri poti ;) Nadaljujemo v levo stran. Pol levo od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čezenj ne menja predznaka. Modro območje se tako nadaljuje vse do naslednje značilne točke grafa racionalne funkcije, to je ničla na skrajni levi. Vrednost funkcije v ničli pa je seveda nič ;) Nadaljujemo z risanjem grafa. Ostajamo v negativnem (modrem) območju, zato se graf vrne z iste strani, v katero je izginil, ko smo se približevali polu. Z grafom nato preprosto nadaljujemo proti ničli na levem robu modrega območja. Naj vas še enkrat opozorimo: črta naj ne bo ravna, saj nimamo linearne funkcije! Sedaj pa pojdimo še malo v desno stran. Ničla desno od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čeznjo prav tako ne menja predznaka. Negativno (modro) območje se tako nadaljuje tudi v desno - do naslednje značilne točke grafa racionalne funkcije, pola na skrajni desni. Vrednost funkcije v polu pa ni definirana. Pozor! Zaenkrat naša racionalna funkcija nikjer ni pozitivna, kar pa ne pomeni, da je vedno negativna! V ničlah je vrednost funkcije nič, v polih pa ni definirana. Z risanjem grafa nadaljujemo v desno smer. Zopet smo v negativnem (modrem) območju, zato se graf desno od ničle obrne navzdol. Nadaljujemo v desno, do meje obarvanega območja. Ker se na skrajni desni nahaja pol, graf zavije navzdol proti neskončnosti. Ničla na skrajni levi strani je lihe (prve) stopnje, zato funkcija pri prehodu čeznjo menja predznak (iz negativnega v pozitivnega). Levo od te ničle ni nobene značilne točke grafa več, zato se pozitivno (rdeče) območje nadaljuje levo v neskončnost. Narišimo še zadnji odsek grafa na levi strani koordinatnega sistema. Ker se na skrajno levi ničli predznak funkcije zamenja (iz negativnega v pozitivnega), z grafom nadaljujemo levo od te ničle navzgor. Pozor! Navzgor ne pojdimo preveč daleč, saj se graf pri zelo majhnih vrednostih x (levo v neskončnosti) približuje vodoravni asimptoti! Zato naredimo "ovinek" navzdol in z grafom funkcije nadaljujemo naprej proti asimptoti. Če želimo graf na tem (rdečem) območju še točneje narisati, si lahko izberemo kakšno dodatno točko, v kateri izračunamo vrednost racionalne funkcije in jo vrišemo na koordinatni sistem (na primer f(-4), to je vrednost funkcije pri x=-4). Določimo predznak še na zadnjem območju grafa racionalne funkcije. Pol na skrajni desni strani je lihe (prve) stopnje, zato funkcija pri prehodu čezenj menja predznak (iz negativnega v pozitivnega). Desno od tega pola ni nobene značilne točke grafa več, zato se pozitivno (rdeče) rdeče območje nadaljuje desno v neskončnost. Narišimo še zadnji odsek grafa na desni strani koordinatnega sistema.
Ker se na skrajno desnem polu predznak funkcije zamenja (iz negativnega v pozitivnega), se graf na drugi strani pola ne vrne z iste strani, v katero je izginil (navzdol), ampak z nasprotne (od zgoraj). Ker se graf racionalne funkcije pri zelo velikih vrednostih x (desno v neskončnosti) približuje vodoravni asimptoti, le-ta naredi zavoj v desno (brez ostrih robov!) in se nadaljuje naprej proti asimptoti. Pozor! Abscisne osi (x) na tem odseku ne smemo več sekati, saj v področju desno od pola prve stopnje ni več nobene ničle, graf pa lahko seka abscisno os le pri prehodu preko ničle!
0 Comments
Postopkov je v matematiki celo morje. Eni so bolj "na kožo pisani" enim, drugi drugim. Rdeča nit vseh skupaj pa je - razumevanje. Sam postopek je brez razumevanja matematičnega ozadja povsem brez pomena, saj nikoli ne moremo vedeti, ali smo nekaj izračunali prav ali narobe. Po drugi strani pa tak postopek hitro pozabimo ali si ga zapomnimo površno, kar pa nam tudi prav nič ne koristi :)
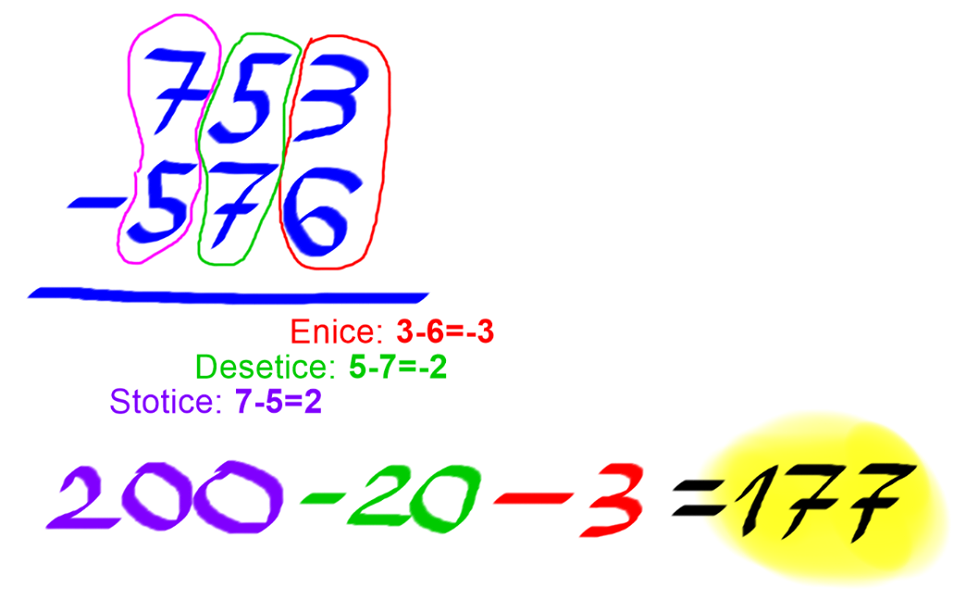
Pri tem postopku se moramo dobro poznati pojem negativnih števil ter razumeti vrednost desetiških enot. Postopek se od "klasičnega" razlikuje po tem, da ne zahteva dopisovanja "malih številk" pri prehodu čez desetico. Le-te namreč lahko kaj hitro zapišemo na napačno stran števke in posledično upoštevamo pri napačni desetiški enoti (še posebej, če nas različni učitelji navajajo na zapisovanje na različnih straneh), kar vodi k nepravilnemu rezultatu. Kot vidimo v spodnjem primeru, nam pri deseticah preglavice povzroča prehod čez stotico, pri enicah pa prehod čez desetico, zato najprej odštejemo le stotici, omenjena prehoda pa kasneje "korigiramo" z odštetjem "odvečnih" desetic in enic (če smo natančni, prištetjem negativnih desetic in enic). Kako si zapomniti, katera številka v ulomku je števec in katera imenovalec?
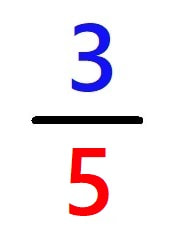
Števec spominja na štetje in je zgoraj, saj imamo eno tretjino, dve tretjini ... Imenovalec nas pa spominja na poimenovanje in je spodaj. Tako imamo eno tretjino, eno četrtino ... Recimo: "Pozdravljeni, ime mi je Petina in živim v spodnjem nadstropju ulomka." :) No, sedaj pri kontrolni nalogi sigurno ne boste več zamenjavali števca in imenovalca in na ta račun izgubili kakšne pomembne točke ;) Veste, da lahko z eno samo vajo "opravite" s kar tremi računskimi operacijami oziroma postopki? Oglejmo si, kako lahko naenkrat utrjujemo:
Vaja je sestavljena iz treh delov. Najprej pisno zmnožimo dve števili in si zabeležimo rezultat, saj ga bomo še potrebovali. Množitelj je lahko eno- ali dvomestno število, odvisno od razreda in volje ;) V drugem delu vaje množenec razstavimo na desetiške enote (v našem primeru stotice, desetice in enice) in vsako posebej množimo z množiteljem. Ko posamezne zmnožke seštejemo, dobimo isto število kot v prvem koraku. S tem smo s pomočjo zakona distributivnosti (več o njem na naslovu tinyurl.com/yctv72wg) dokazali pravilnost izračuna v prvem koraku. Izračun seveda lahko preverimo tudi s kalkulatorjem, ampak če smo ga na dva načina rešili enako, si pa že lahko zaupamo ;) V zadnjem delu pa račun še "obrnemo".
Sedaj zmnožek iz prvega in drugega dela (upajmo, da v obeh primerih dobimo enakega ;) ) delimo z množiteljem in če gre vse tako, kot mora iti, dobimo "nazaj" množenca. S tem smo opravili še končni preizkus in lahko rečemo, da zadevo obvladamo ;) |
ARHIV
May 2024
KATEGORIJE
All
|



 RSS Feed
RSS Feed
