|
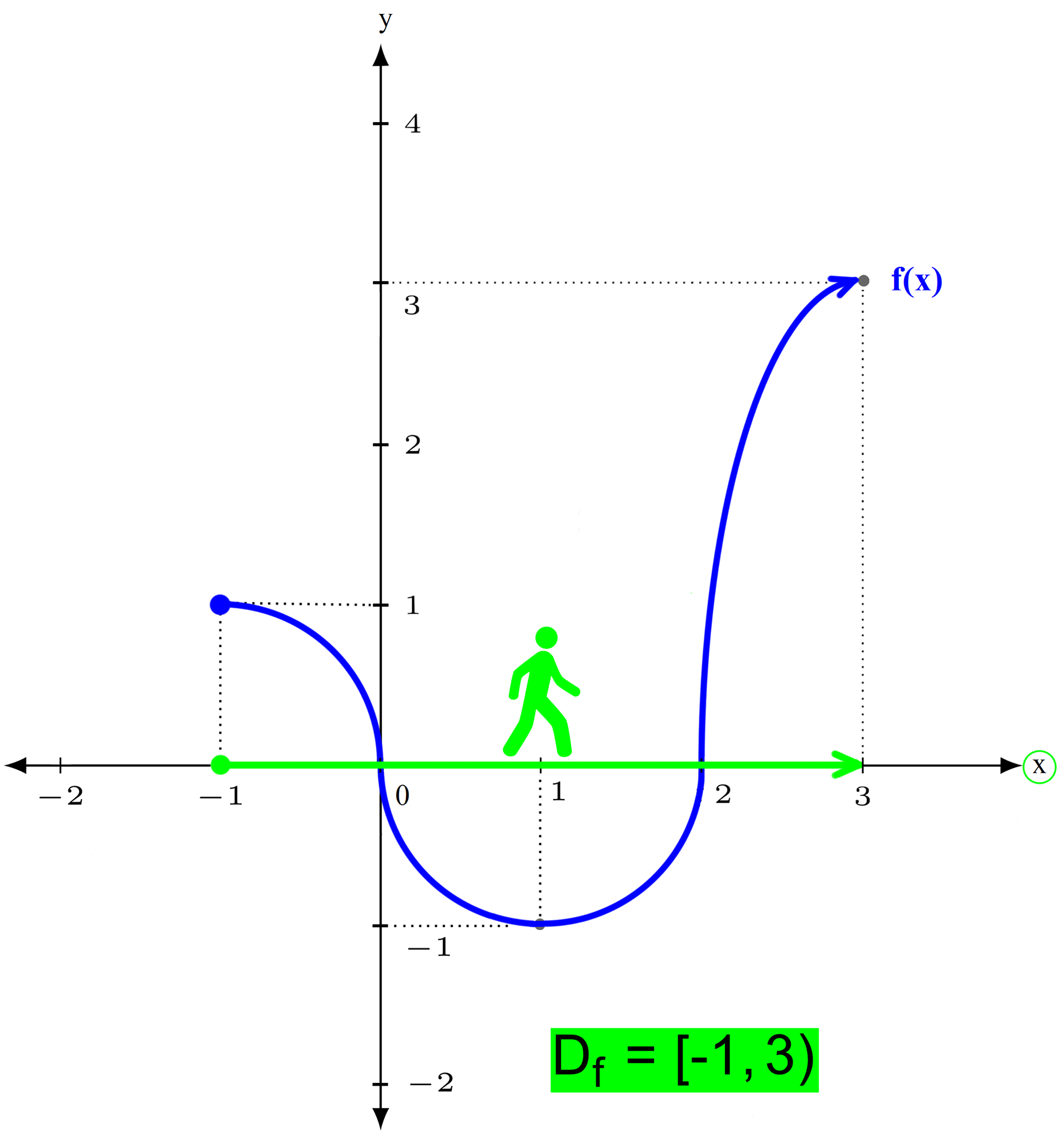
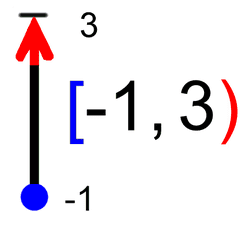
Ste se kdaj "zataknili" pri definicijskem območju ali zalogi vrednosti? Govorimo seveda o funkcijah, takih in drugačnih, vsaki z zvrhanim košem lastnosti :) Da pred tablo ali na pisnem testu ne boste "debelo gledali", vam predstavimo nekaj idej, kako funkciji določiti lastnosti na čim lažji način. Definicijsko območje Začnimo z definicijskim območjem, ki smo ga malo prej že omenili. Kot vemo, funkcija preslika neodvisno spremenljivko (največkrat je to x) v odvisno spremenljivko (običajno y). In definicijsko območje pomeni tiste vrednosti x, ki se bodo preslikale v y. Jap, ne pridejo vedno vse na vrsto za preslikavo ;) Definicijsko območje si je najlažje predstavljati na grafu funkcije. Zamislite si, da ste možak na spodnji sliki. Hodite po abscisi koordinatnega sistema (to je x os) od leve proti desni strani (v tej smeri tudi pišemo). Pri hoji se ozirate navzgor in navzdol, če boste kje videli funkcijo. Del poti, kjer je funkcija vidna, pobarvate z zeleno (tako kot je označeno na spodnji sliki). Interval, ki ste ga narisali (obarvan zeleno), je definicijsko območje funkcije:
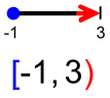
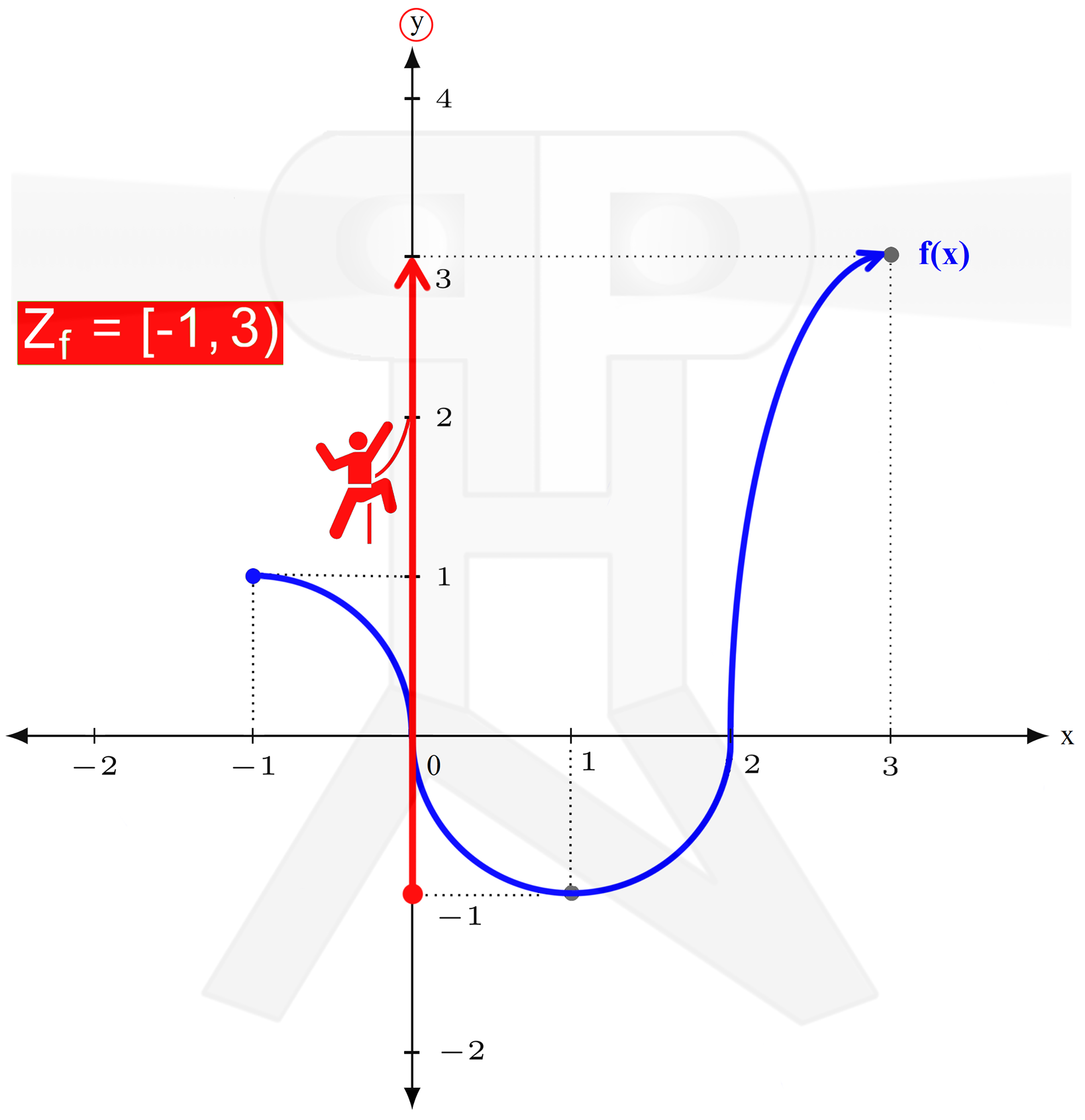
V našem primeru začetna točka spada zraven, končna pa ne. Temu primeren je tudi zapis definicijskega območja. Zaloga vrednosti Poleg definicijskega območja običajno vedno navedemo tudi zalogo vrednosti. Če so definicijsko območje tiste vrednosti x, ki se bodo preslikale v y, so "zaloga vrednosti" vse vrednosti y, ki so pri preslikavi nastale. Poenostavljeno bi lahko rekli, da se je definicijsko območje preslikalo v zalogo vrednosti. Tudi zalogo vrednosti si najlažje predstavljamo na grafu funkcije. V prejšnjem poglavju smo bili "zelen sprehajalec", sedaj pa bodimo "rdeč plezalec" ;) Včeraj smo hodili, danes pa plezamo, navpično navzgor, po ordinati koordinatnega sistema (y os). Plezati začnemo v najnižji točki grafa funkcije in splezamo vse do njenega vrha. Ker nam plezanje ne dela težav, zraven še malo pleskamo, tokrat z rdečo barvo :)
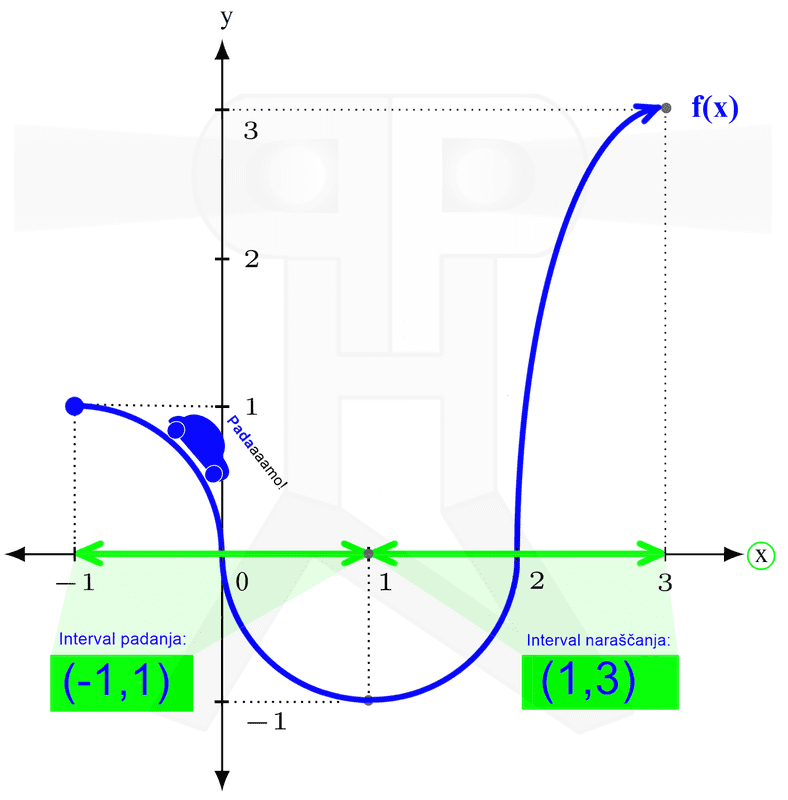
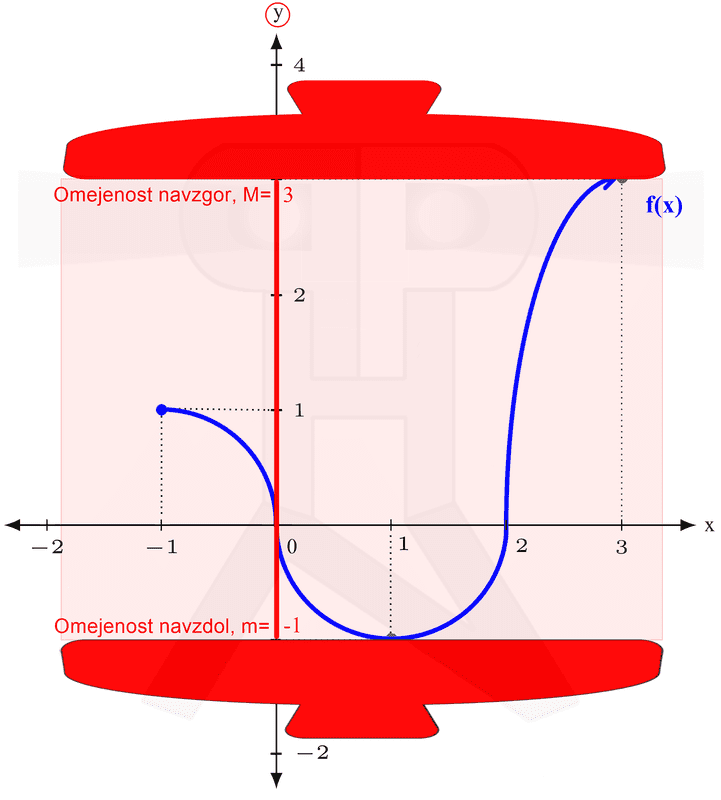
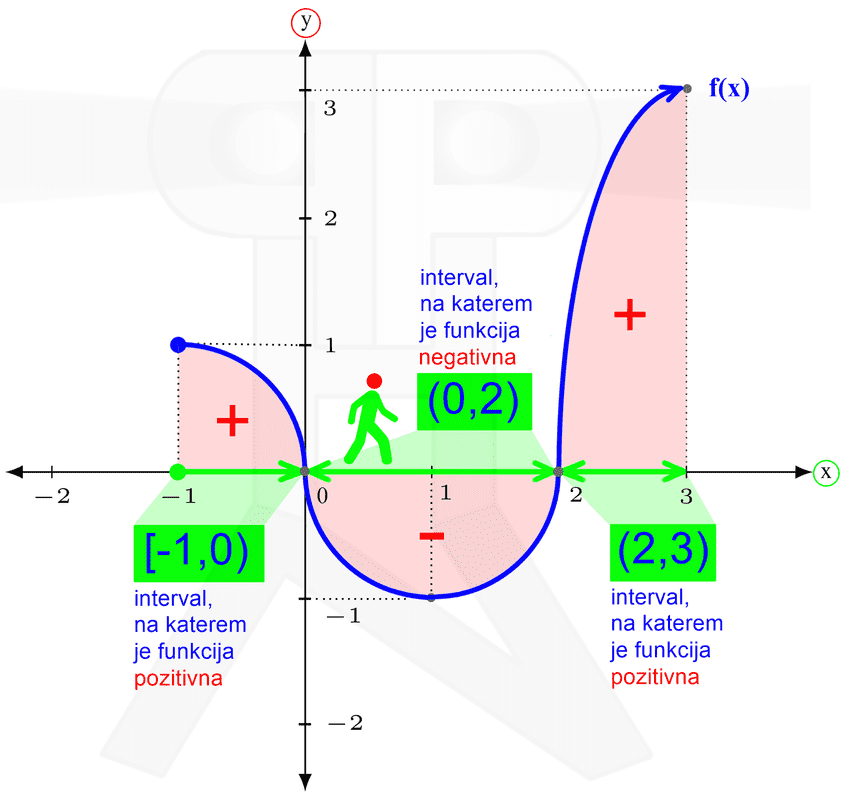
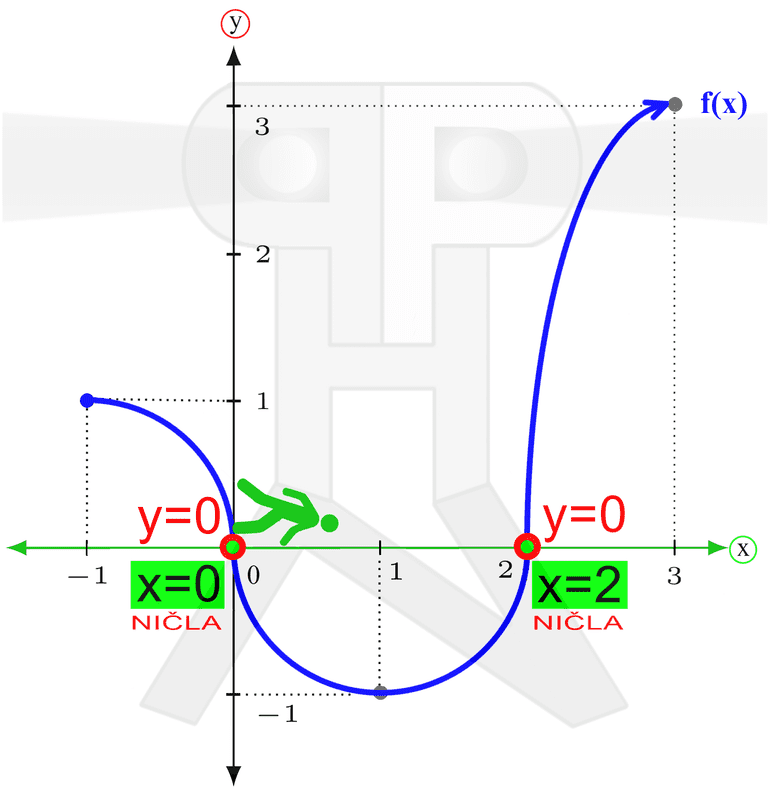
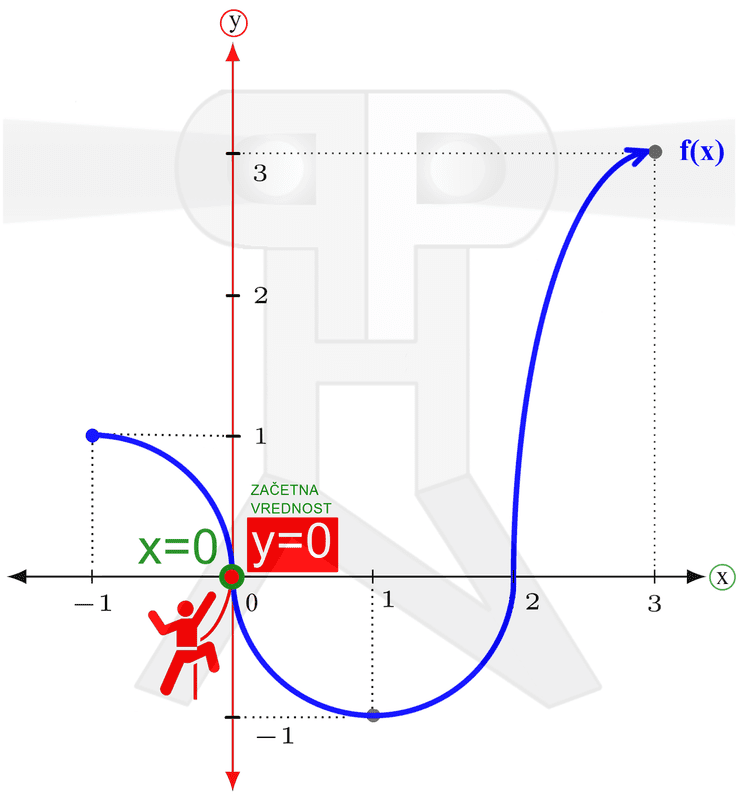
V našem primeru najnižja točka spada zraven, najvišja pa ne. Temu primeren je tudi zapis zaloge vrednosti. Naraščanje in padanje Na kratko: zanima nas, pri katerih vrednostih (neodvisne) spremenljivke x funkcija narašča in pri katerih vrednostih pada. Vrednosti spremenljivke x seveda ne naštevamo, ker bi jih bilo preveč, ampak jih podajamo v obliki intervalov. Spremenljivki x pripadajo "vodoravni" intervali, ki smo jih srečali že pri obravnavi definicijskega območja in so na naših slikah obarvani zeleno. Intervale naraščanja in padanja najlažje razberemo z grafa funkcije. Do sedaj smo tekli in plezali, tokrat pa se peljimo z avtomobilom. Peljemo se po (modri) krivulji funkcije od leve proti desni (v tej smeri tudi pišemo) in smo pozorni na to, ali se peljemo "v klanec" ali "s klanca". Ko gremo navzgor, funkcija narašča, ko gremo navzol, pa pada: Naj omenimo še to, da točke, kjer graf iz padanja preide v naraščanje (in obratno), ne spadajo v intervale naraščanja oz. padanja, zato so oklepaji v zapisu intervalov vedno okrogli. Ne pozabimo: če graf "pride iz neskončnosti" oziroma "gre v neskončnost", moramo pa tako ali tako uporabiti okrogli oklepaj! Omejenost Funkcija je lahko omejena navzgor, navzdol ali pa kar v obe smeri (in ne na levo in desno, kot se včasih kdo rad zmoti). Vsi ste že kdaj merili svojo višino. Če ne drugače, so vas izmerili na sistematskem pregledu. Na podoben način lahko "izmerimo" tudi funkcijo, s to razliko, da ne bomo podali njene višine, ampak le najnižjo in najvišjo točko. Zopet si pomagajmo z grafom funkcije. Zamislimo si dve veliki pokrovki (na sliki rdeče barve), med kateri "ulovimo" funkcijo. Zakaj ravno pokrovki? Zato, da bo zares "odbito" in si boste zato bolj zapomnili :) Položaj spodnje pokrovke na navpični (y) osi nam pove spodnjo mejo funkcije (označimo jo z malo črko m), položaj zgornje pokrovke na y osi pa nam pove zgornjo mejo funkcije (označimo jo z veliko črko M). Včasih se zgodi, da funkcije ne moremo "ujeti v pokrovko". V tem primeru funkcija navzdol oz. navzgor ni omejena. Kakšne niso omejene navzgor, druge navzdol, se pa najdejo tudi take, ki sploh niso omejene. Pozitivnost in negativnost Poglejmo, pri katerih vrednostih x je funkcija pozitivna oziroma negativna. Tudi tu vrednosti spremenljivke podajamo v obliki intervalov ("vodoravni" intervali, obarvani zeleno) Spomnimo se poglavja o definicijskem območju, kjer se je zelen možak oziral navzgor in navzdol ter preverjal, kje je funkcija vidna. Takrat ga ni zanimalo, ali je funkcija nad ali pod njim, sedaj pa je to pomembno (zato smo možaku glavo obarvali rdeče). Kadar je funkcija nad možakom, je le-ta pozitivna, kadar pa je pod njim, pa je negativna: Točke, kjer graf seka x os, ne spadajo v intervale pozitivnosti oz. negativnosti (uporabimo okrogli oklepaj!), saj tam funkcija ni ne pozitivna in ne negativna, ampak je njena vrednost enaka nič. Te točke imenujemo ničle funkcije. K njim se še vrnemo v nadaljevanju. Ne pozabimo: Če graf "pride iz neskončnosti" in/ali "gre v neskončnost", moramo na začetku prvega in/ali na koncu zadnjega intervala uporabiti okrogli oklepaj! Ničle funkcije Nekaj vrstic nazaj smo iskali vrednosti (neodvisne) spremenljivke x, pri katerih je funkcija pozitivna oziroma negativna. In kakšno vrednost ima funkcija, če ni niti pozitivna, niti negativna? Nič, seveda :) Točke, v katerih ima funkcija vrednost 0, imenujemo ničle funkcije. Nahajajo se na abscisni (x) osi koordinatnega sistema. Ne pozabimo: v ničlah je y enak 0, medtem ko vrednost "ničle" pove x! Na grafu ničle funkcije izgledajo kot neki kamni na zeleni poti (vodoravna x os), ob katere se spotika naš možic, ki smo ga že kar nekajkrat srečali: V ničli graf seka ali pa se dotika (zeleno označene) x osi. Graf seka x os v ničlah "lihega reda" (stopnje 1,3,5,...), dotika se ga pa v ničlah "sodega reda" (stopnje 2,4,6,...). V našem primeru sta ničli dve. Prva ima vrednost 0, druga pa vrednost 2. Označeni sta z zelenim okvirčkom. Začetna vrednost funkcije V nasprotju z ničlami, ki smo jih obravnavali nekaj vrstic višje, tokrat 0 ni vrednost funkcije, ampak vrednost neodvisne spremenljivke x. Ne pozabimo: v točki, ki označuje začetno vrednost, je x enak 0, medtem ko začetno vrednost podajamo z y! Na grafu začetna vrednost izgleda kot nek "oprijemek" na rdeči steni (navpična y os), po kateri pleza naš možic, ki smo ga že kar nekajkrat srečali: V tej točki, ki označuje začetno vrednost, graf funkcije seka (rdeče označeno) y os.
V našem primeru je začetna vrednost enaka 0. Označena je z rdečim okvirčkom.
2 Comments
Navodila, ki sledijo, vam bodo prišla prav pri domačih nalogah ter matematičnih testih, tudi na NPZ-jih ter maturi. A veste, tisto, ko si ves nervozen, do konca testa je le še 10 minut, pa ne veš točno, kaj naloga sploh hoče od tebe?!? No, tega, upamo, da bo sedaj manj ;) Poenostavi! Pri taki nalogi najprej z množenjem in potenciranjem odpravimo oklepaje (izraz razširimo), na koncu pa "zložimo" skupaj podobne člene ter konstante: V šali včasih kdo reče: "Pa ne moreš seštevati jabolk in hrušk!" In prav ima! Hrušk in jabolk seveda ne moremo sešteti skupaj, lahko pa seštejemo oziroma odštejemo vsake posebej. V nalogah lahko namesto "Poenostavi!" zasledimo zahtevo "Skrči izraz!" Navodili za reševanje sta pri obeh enaki. Enemu učitelju je pač bolj všeč en, drugemu pa drug način podajanja navodila za reševanje naloge. Razstavi! V matematiki ima (skoraj) vsaka operacija svojo inverzno operacijo. Naj navedemo nekaj takšnih "parov":
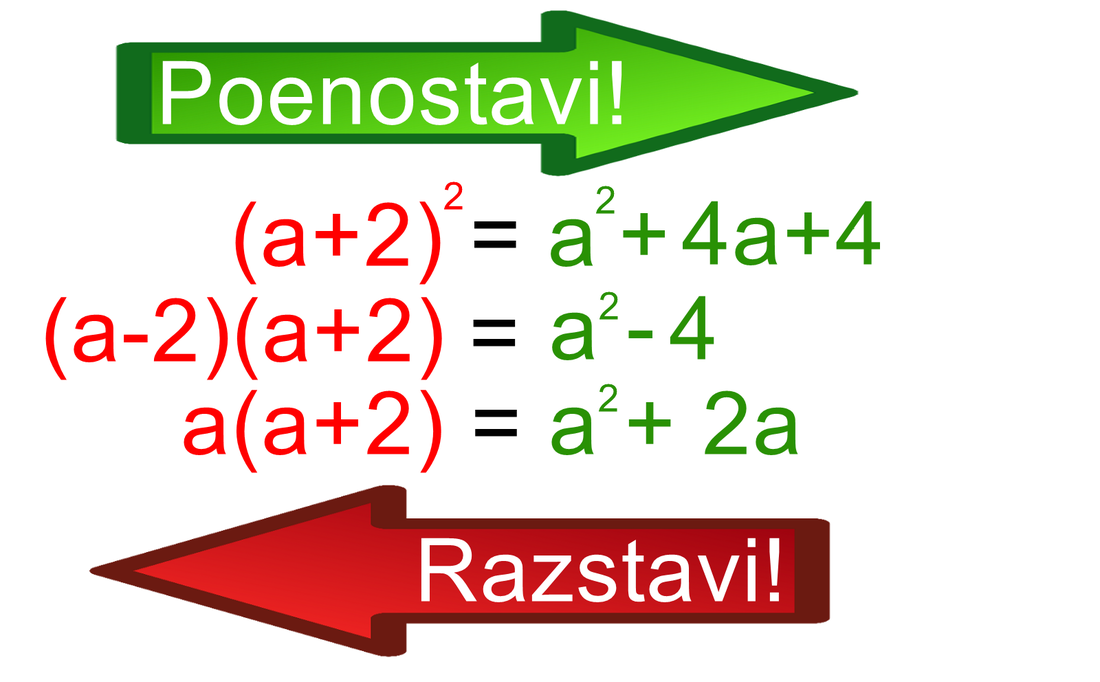
Tako ima tudi navodilo "Poenostavi!" svojo inverzno različico, ki se glasi: "Razstavi!" Razliko med njima najbolje ponazorijo naslednji primeri: Pomembno je, da si zapomnite naslednje:
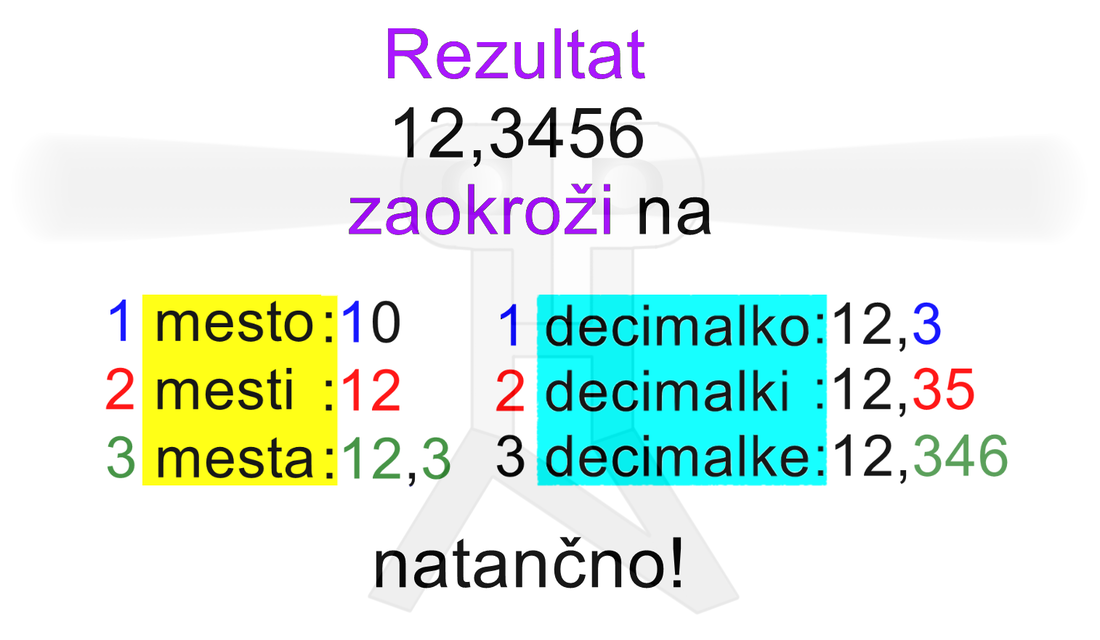
Reši! Kaj lahko na matematičnem testu "rešimo"? Enačbo ali neenačbo. In zakaj ravno "rešimo"? Predstavljajte si, da ste superjunak, ki iz krempljev strašne enačbe rešite spremenljivko (največkrat je to "x"). No, sedaj ste dobili odgovor :) Reševanje (ne)enačb je podobno kot poenostavljanje izrazov, s to razliko, da imamo pri (ne)enačbah nekaj členov na levi in nekaj členov na desni strani (ne)enačaja, medtem ko je pri izrazih vedno vse na levi strani enačaja, kar ponazarja tudi primer: Naredi preizkus! Vsa umetnost preizkusa je ponovni zapis enačbe in zamenjava neznanke (v našem primeru je to "x") z vrednostjo, ki smo jo izračunali oziroma "rešili iz krempljev strašne enačbe" :) Sedaj le še izračunamo, kar smo dobili in - če je leva stran enačbe enaka desni, je enačba pravilno rešena. Če naredimo preizkus, vedno vemo, koliko točk bomo dobili pri taki nalogi, še preden jo učitelj(ica) preveri oziroma "popravi", kot včasih radi rečemo. Izračunaj! Če moramo nekaj izračunati, v rezultatu dobimo same številke. Tudi rešitev (ne)enačbe je številka, kot smo videli včeraj. Za primerjavo: pri poenostavljanju v rezultatu poleg številk dobimo tudi spremenljivke (x, y, a, b,...) - razen takrat, ko se le-te okrajšajo: Nekatere naloge so pa še bolj "zvite": izraz moramo najprej poenostaviti, nato pa ga za podane številske vrednosti spremenljivk še izračunamo. Zaokroži! Če je rezultat realno število (ima neskončen decimalni zapis), ga lahko zapišemo točno ali pa ga zaokrožimo. Najprej si oglejmo zaokrožanje. Rezultat lahko zaokrožimo na dva načina:
Pri zaokroževanju je potrebno vedno "pokukati" še za eno mesto naprej (desno od zadnje števke, ki nas še zanima):
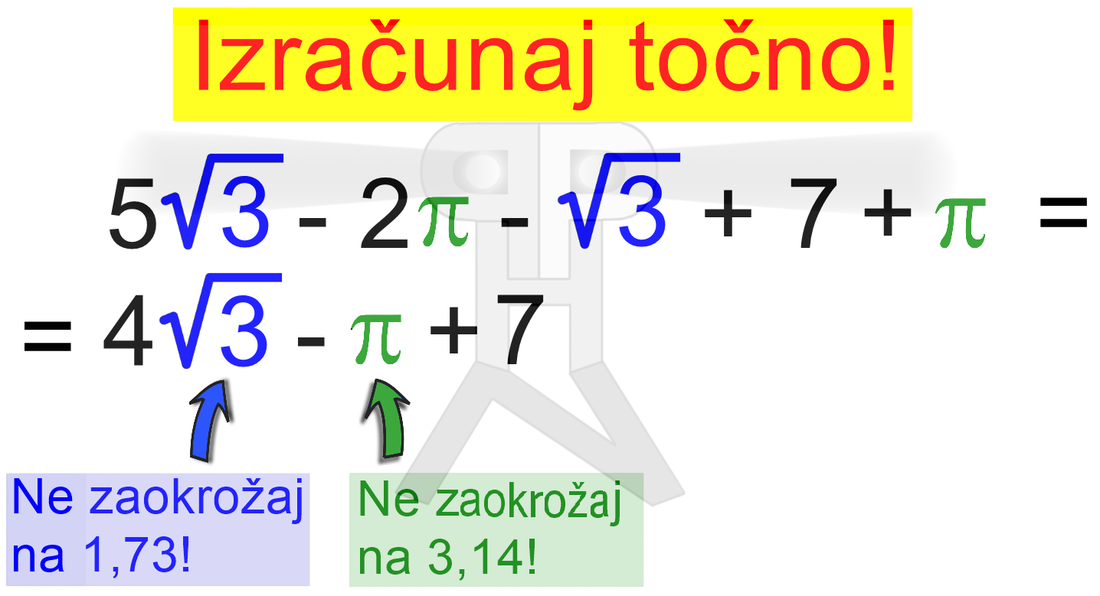
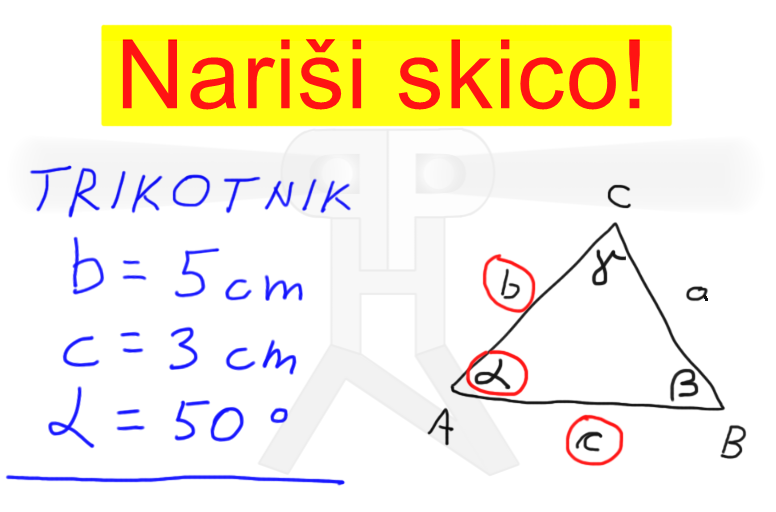
Izračunaj točno! Če želimo rezultat, v katerem nastopajo koreni ter matematične konstante, ki se jih ne da zapisati brez zaokrožanja (npr. π ali e), zapisati točno oz. natančno, teh števil ne smemo zaokrožati, ampak jih pišemo v prvotni obliki, torej koren ostane koren, posebna števila pa ostanejo zapisana z znakom, ki jih določa. Ne pozabimo pa izraza s takimi števili poenostaviti, torej sešteti oziroma odšteti vse enake korene ter posebna števila: Nariši skico! Posvetimo se še nekoliko geometriji. Če naloga od nas zahteva skico, to pomeni, da nam ni potrebno risati z ravnilom in šestilom, prav tako nam ni potrebno paziti na pravilno razmerje med stranicami, koti... Priporočljivo pa je, da stranice, kote in ostale spremenljivke označimo pravilno, podatke iz naloge pa obkrožimo ali kako drugače izpostavimo, saj nam bo to koristilo pri konstruiranju, ki skoraj vedno sledi risanju skice. Konstruiraj!
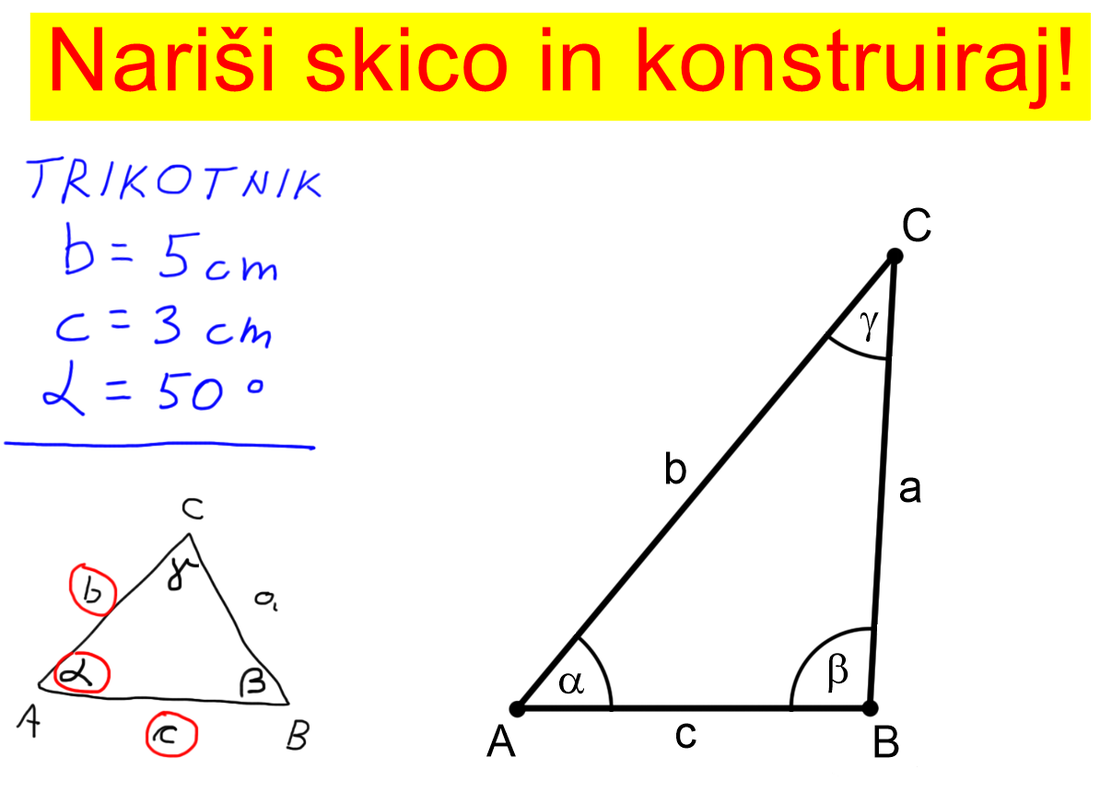
Kot smo že povedali, risanju skice običajno sledi konstruiranje. Le-tega se lotimo z ravnilom (najboljši je geotrikotnik, ki ima zraven še kotomer) in šestilom. Pri konstruiranju lika morajo biti za razliko od skice tako koti kot dolžine (stranic, višin, težiščnic,...) točno taki, kot v podatkih. |
ARHIV
May 2024
KATEGORIJE
All
|
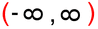





 RSS Feed
RSS Feed
