|
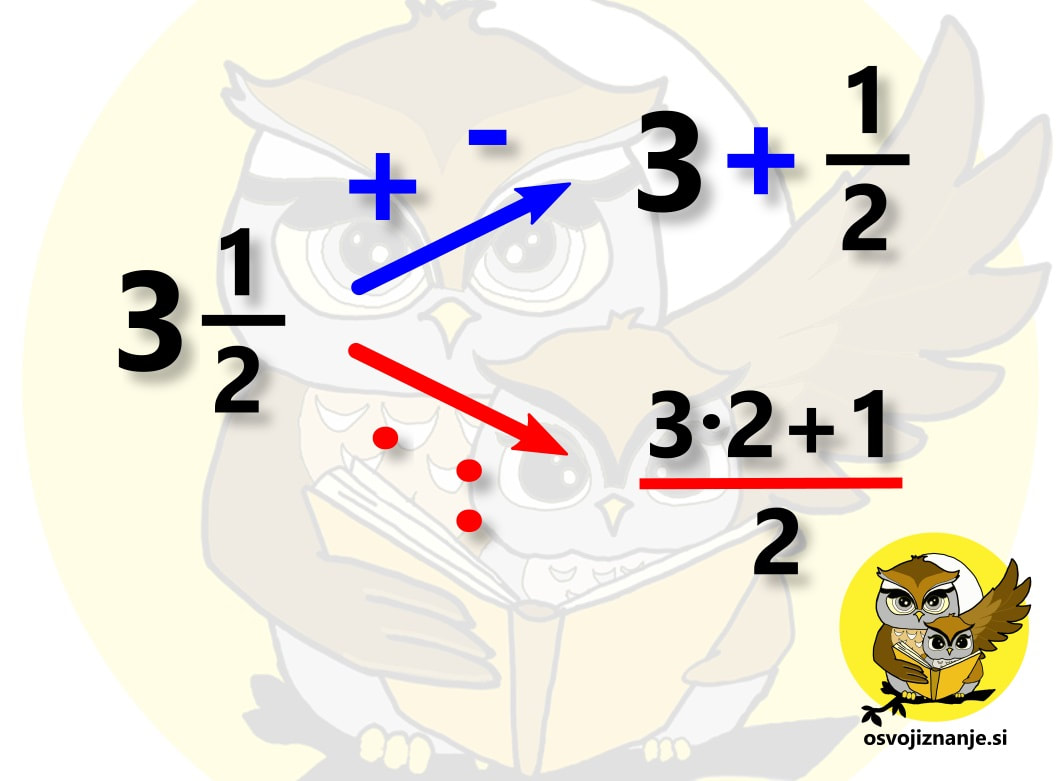
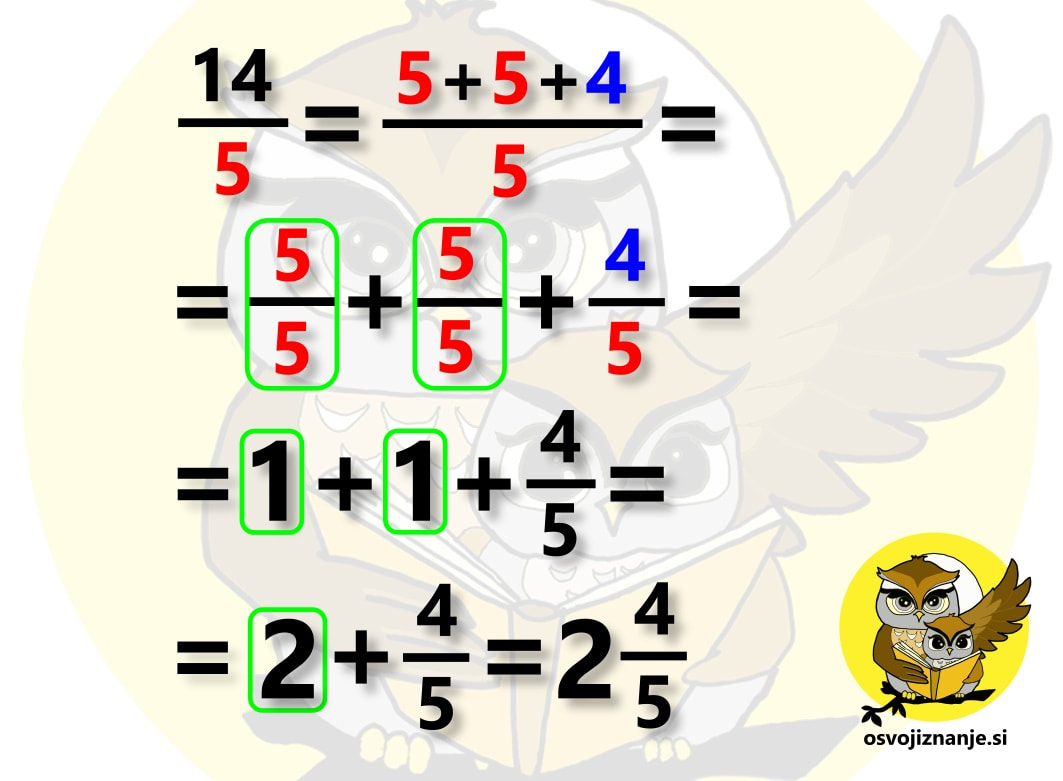
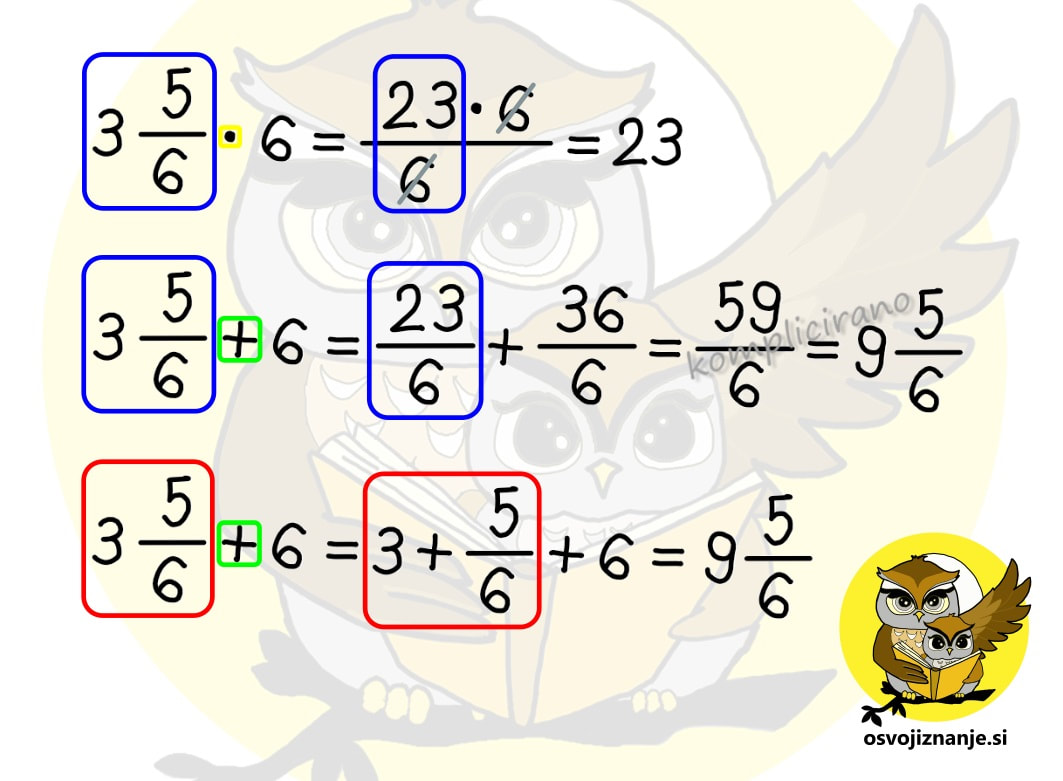
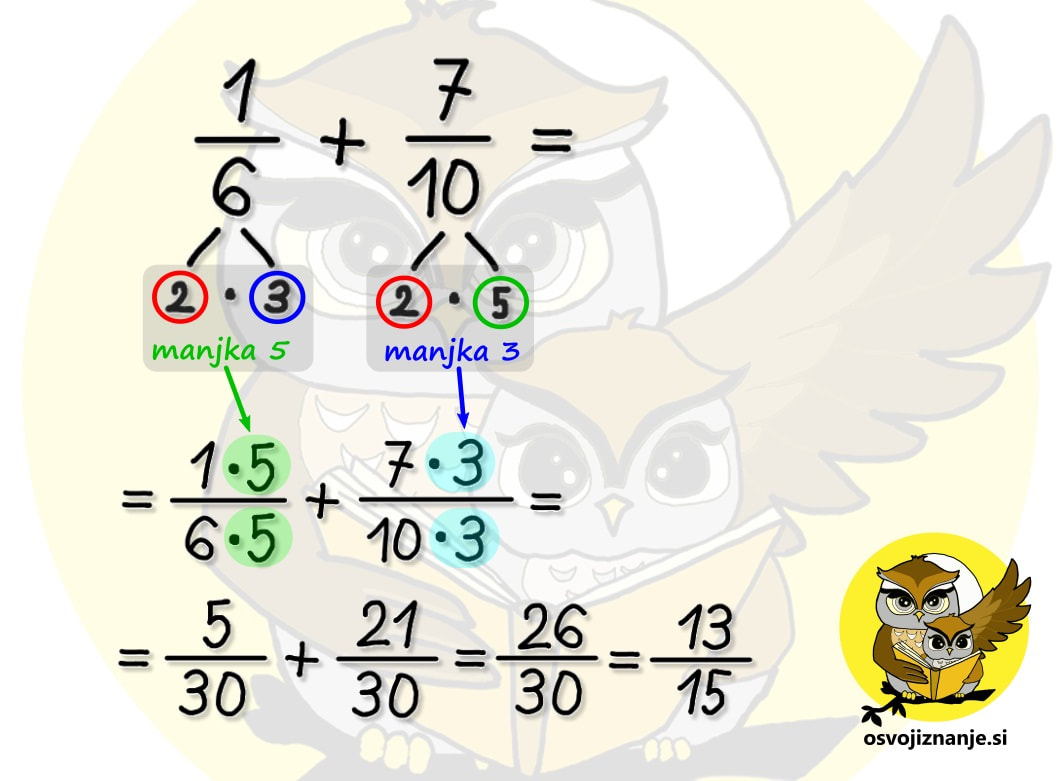
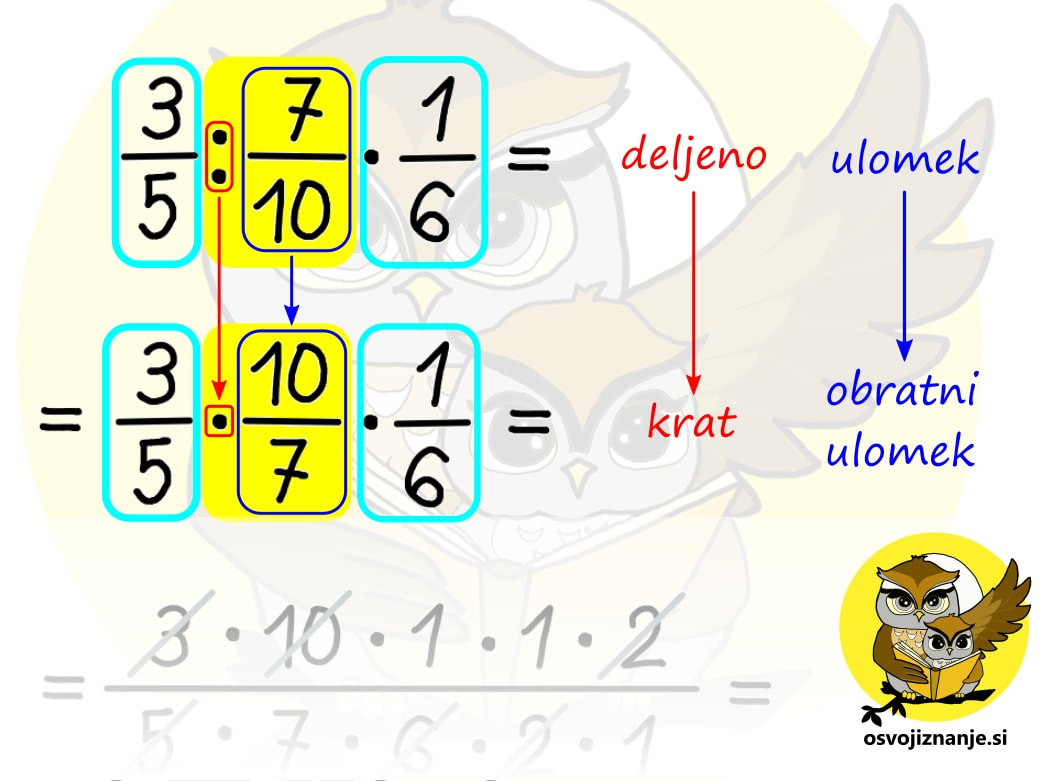
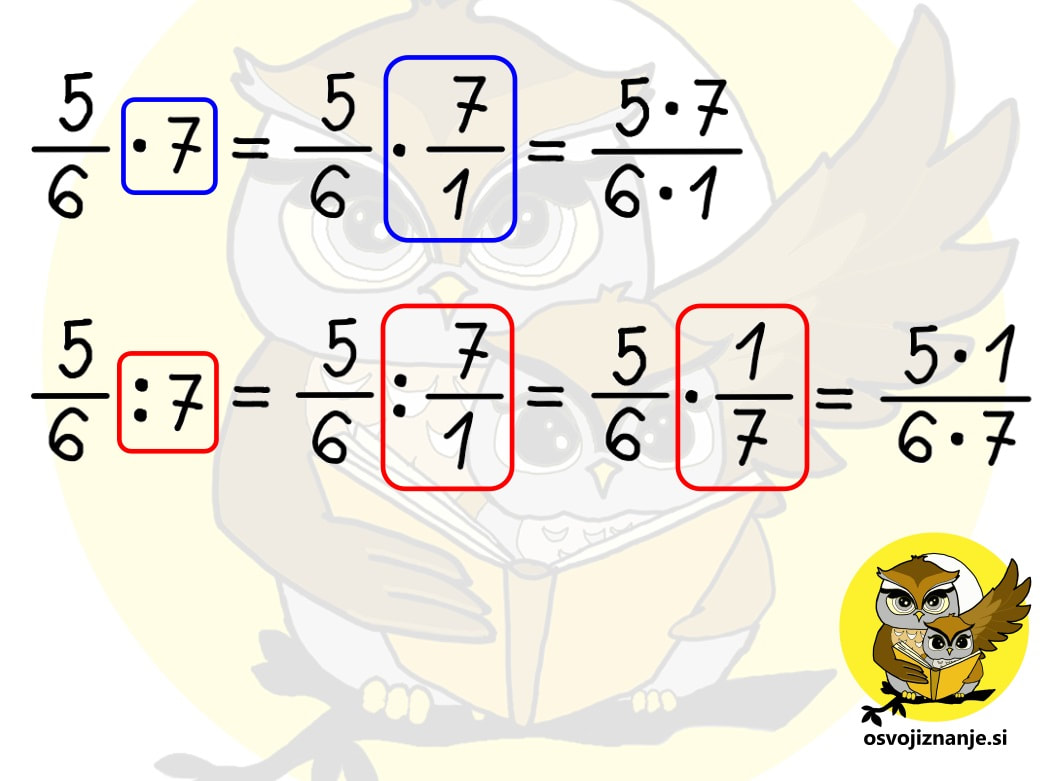
Sedmi razred je pri matematiki za marsikoga kar zalogaj. Praštevila, nato pa ulomki in vse kar pride zraven – krajšanje, razširjanje, primerjanje, iskanje skupnega imenovalca ... in seveda računanje z ulomki. Najprej osnovne računske operacije (seštevanje, odštevanje, množenje in deljenje), nato pa kombinacije le-teh. Da je zadeva še bolj zanimiva, se ulomkom pridružijo še cela, mešana in decimalna števila. Pri obravnavi snovi se seveda vedno mudi in kdor je v nižjih razredih »prešprical« kakšno snov ali pa jo zgolj pozabil (vsi smo ljudje), se hitro znajde v težavah. Da v takih primerih ne bi bilo potrebno takoj klicati inštruktorja, sem pripravil nekaj hitrih nasvetov za »spopad z ulomki«. :) Kako obravnavati mešano število? Mešano število je število, ki je sestavljeno iz celega števila in ulomka, na primer 3 in ena polovica (glej sliko). Marsikdo ob pogledu na tako število začne v imenovalcu takoj množiti 3 z 2 in prištevati 1 ... (spodnji ulomek na desni strani slike). To je seveda pravilen postopek, a ga ni »modro« uporabljati v vseh primerih, ampak le pri množenju in deljenju. Pri seštevanju in odštevanju pa je mešani ulomek lažje zapisati »na dolgo« in sicer v obliki celo število + ulomek (zgornji ulomek na desni strani slike). Zakaj »na dolgo«? Zato, ker je zapis mešanega števila v bistvu skrajšan zapis vsote celega števila in ulomka. Kako odšteti ulomek od celega števila? V takem primeru lahko uporabimo t.i. »strategijo izposojanja«. V našem primeru na spodnji sliki si od 3 »izposodimo« 1, ki jo nato zapišemo v obliki ulomka. Število 1 v obliki ulomka zapišemo tako, da izenačimo vrednost števca in imenovalca, ta pa je lahko karšna koli celoštevilska vrednost. Ker v našem računu nastopa še en ulomek, ki ima vrednost imenovalca 7, enako vrednost uporabimo tudi pri ulomku, ki predstavlja celoto, saj nam tako ni potrebno iskati skupnega imenovalca. Enako strategijo lahko uporabimo tudi pri odštevanju ulomka od mešanega števila, če je ulomek, ki ga odštevamo, večji od ulomka zraven celega števila (npr. 5 2/5 – 3/5). Kako odšteti mešani ulomek? Za mešani ulomek vemo, da je skrajšan zapis vsote celega števila in ulomka. Če tak ulomek prištevamo, lahko enostavno zapišemo celo število + ulomek. Če pa ga odštevamo, ne smemo pozabiti, da minus pred njim »zagrabi« tako na celo število kot na ulomek (podobno kot če bi imeli oklepaj), zato je potrebno odšteti tako celo število kot ulomek. Kdaj je priporočljivo »nepravi ulomek« spremeniti v mešano število in kako to storim? Če ima ulomek »zgoraj več kot spodaj« oziroma ima števec večji od imenovalca, zanj rečemo, da je nepravi. Tak ulomek je »vreden« več kot 1, zato »lepše«, če ga zapišemo kot vsoto celega števila in ulomka oziroma »tistega, kar ostane«. Vemo, da ulomke seštevamo tako, da števce seštejemo, imenovalec pa prepišemo. Kaj pa, če bi to pravilo uporabili »v rikverc«? Števec ulomka lahko zapišemo kot vsoto vrednosti v imenovalcu in ji prištejemo »tisto, kar ostane«. V našem primeru števec 14 zapišemo kot vsoto dveh petic in »preostale« štirice (5+5+4). Tak ulomek lahko razdelimo na 3 ulomke (5/5, 5/5 in 4/5), od katerih sta prva dva enaka 1, zato ju lahko zapišemo kot celoštevilsko vrednost 2, zadnji ulomek (4/5) pa dopišemo zraven. Kdaj moram mešano število spremeniti v »nepravi ulomek« in kako to storim? Takrat, kadar mešano število množimo ali delimo s celimi števili ali ulomki. Primer množenja mešanega števila s celim številom je prikazan v prvi vrstici spodnje slike. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Druga in tretja vrstica spodnje slike predstavljata isti račun (seštevanje mešanega števila s celim številom), rešen na dva načina. V drugi vrstici vidimo, da smo iz povsem enostavnega seštevanja znotraj desetice prišli na račun 23+36, katerega rezultat je potrebno potem deliti še s 6, da dobimo celi in ulomljeni del rešitve. V tretji vrstici pa enostavno seštejemo celi števili, prištejemo ulomljeni del in brez pretiranega napora dobimo, seveda, enak rezultat. :) Kako najlažje poiščem (najmanjši) skupni imenovalec? Pred časom sem na inštrukcijah poskusil z metodo »nogic« oziroma »rožičkov«, ki se jo mogoče kdo spomni še iz nižjih razredov osnovne šole. Za razliko vrednosti na krajiščih »nogic« tu ne seštevamo ampak množimo, pred tem pa število razcepimo na prafaktorje. Ker to počnemo grafično, zadeva utegne postati celo zabavna. ;) Več o sami metodi si lahko preberete v članku o računanju s pomočjo številskih dreves. V čem je »trik«? Vzemimo za primer račun s spodnje slike. Prvi seštevanec ima imenovalec enak 6, drugi pa 10. Po razcepu na praštevila na »nogice« prvega imenovalca zapišemo 2 in 3 (2 · 3 = 6), na nogice drugega pa 2 in 5 (2 · 5 = 10). »Fora« najmanjšega skupnega imenovalca je v tem, da s »čim manj potezami« imenovalca izenačimo. Pri tem seveda lahko uporabimo zgolj računsko operacijo množenja, množiti (z istim številom!) pa moramo tako »spodaj« (imenovalec) kot »zgoraj« (števec), sicer vrednost ulomka spremenimo, kar pa ni okej. Poglejmo, kako lahko imenovalca izenačimo v našem primeru. Prvi ulomek »ima« 2 in 3, drugi pa 2 in 5. Z »najmanj potezami« imenovalca izenačimo tako, da na prvi imenovalec dodamo (števec in imenovalec množimo s) 5, na drugega pa 3. Tako sta oba imenovalca enaka 2 · 3 · 5 = 30, števca pa sta po množenju enaka 5 oziroma 21. Ulomka nato še seštejemo in okrajšamo oziroma poenostavimo in dobimo rezultat trinajst petnajstin. Če imamo večja števila, imenovalce lako »drobimo« postopoma (drevo se bolj razveji), upoštevamo pa zgolj številke na končnih vej(ic)ah. Te za boljšo vidnost lahko tudi obkrožimo. Ko smo že nekoliko bolj izkušeni, nam imenovalcev ni potrebno drobiti povsem do praštevil. Če imamo na primer imenovalca enaka 8 in 12, lahko zapišemo 8 kot 2 · 4, 12 pa kot 3 · 4. 4 nam ni potrebno drobiti naprej na 2 · 2, saj se 4 nahaja v obeh imenovalcih s takim »kompliciranjem« ne bi nič pridobili, le hitreje bi se lahko zmotili. :) To je seveda zgolj eden izmed možnih načinov. Če v njem nekako »ne najdete«, pa lahko »pokukate« še tale članek. Kdaj moram »obrniti ulomek«? Računanju z obračanjem ulomka »uradno« rečemo množenje z obratno vrednostjo ulomka. Ker je deljenje z ulomkom »smotano« :) (pojavijo se dvojni ulomki in druge neprijetnosti), raje uberemo drugo pot, pri čemer modro izkoristimo naslednja dejstva:
Iz tega sledi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Obratno vrednost ulomka določimo zelo enostavno, saj zgolj zamenjamo vrednosti števca in imenovalca (ulomek obrnemo »na glavo«). :) Kdaj moramo torej »obrniti ulomek«? Vsakič, kadar računsko operacijo deljenja zamenjamo z množenjem. In zakaj to počnemo? Zato, ker je množenje z ulomkom enostavnejše od deljenja. A ne pozabimo: obrnemo vedno zgolj tisti ulomek, ki stoji desno od znaka za deljenje (ki postane znak za množenje)! Še nekaj za »nerde«. Če potegnemo analogijo s seštevanjem in odštevanjem, lahko zapišemo ...
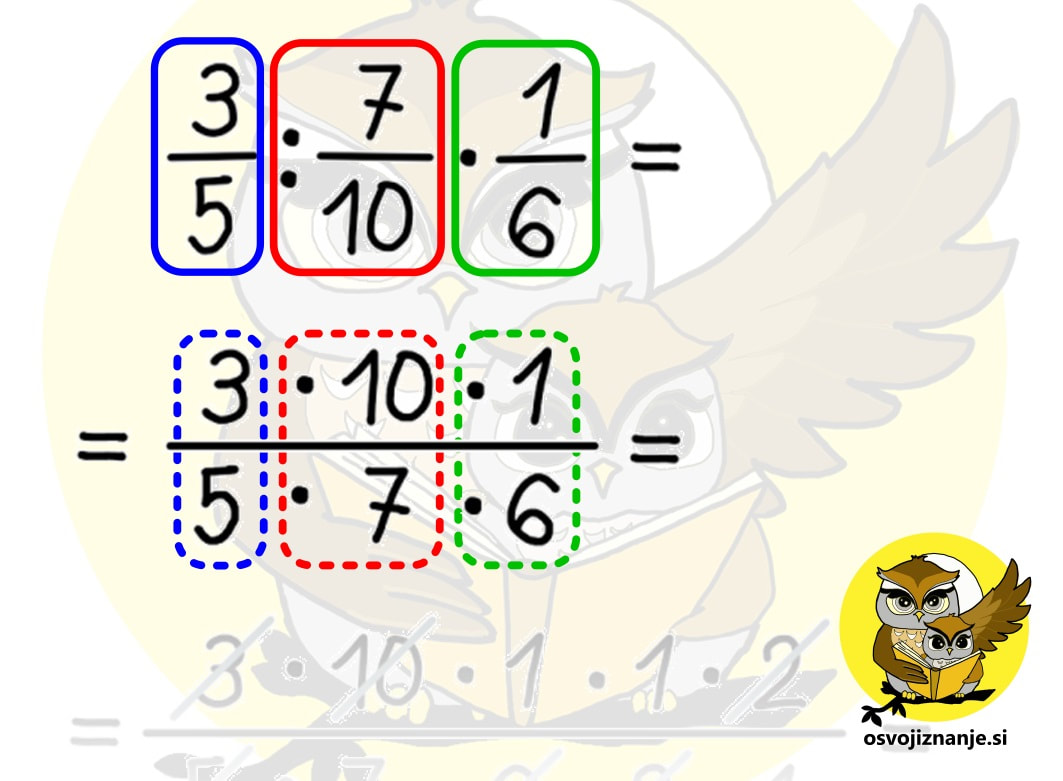
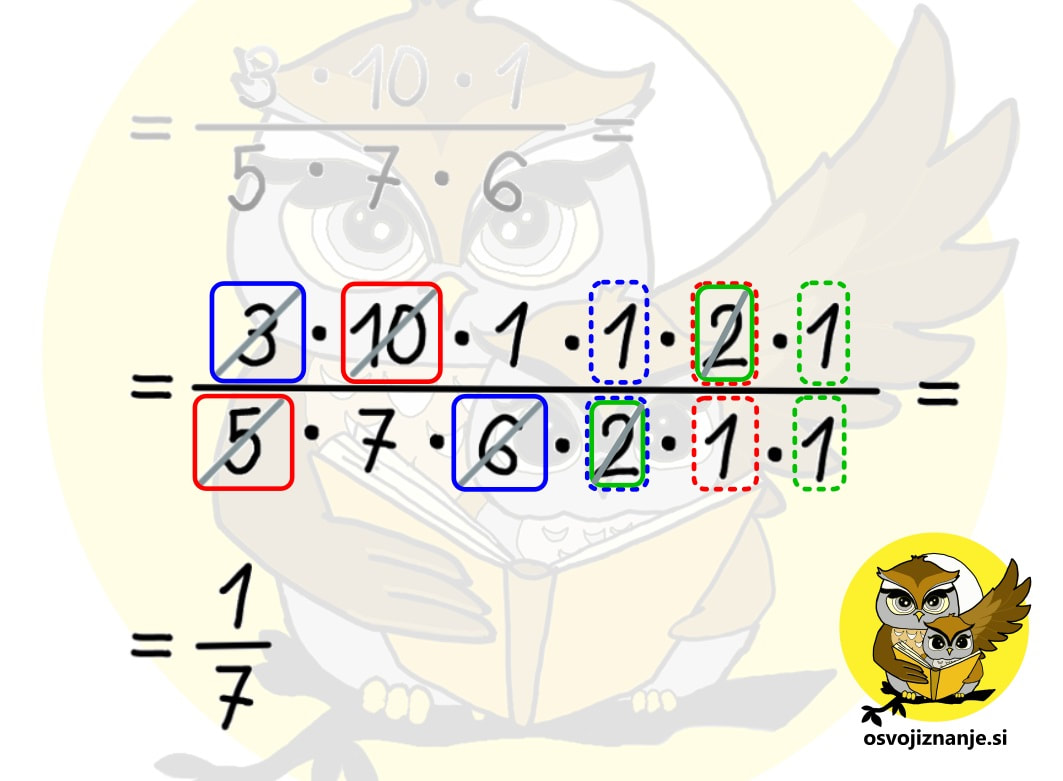
Za konec pa še nekaj za »toplt nerde« :) Vemo, da velja enakost a-(-a) = a+a. Po analogiji bi lahko zapisali tudi a:(:a) = a·a, ampak bi nas kak matematik »za ušesa«. :) Omenjeni zapis namreč ni dovoljen, saj »:« v prvem oklepaju ni predznak, tako kot »-« v drugem oklepaju. Lahko pa drugi zapis popravimo v a:(1:a) = a·a oziroma v a:(1/a) = a·a. Pa smo spet pri naši ugotovitvi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Pa še nekaj. Predznaka »+« nikoli ne pišemo, čeprav »vemo, da je tam«. Zato tudi prvi člen na skrajni levi strani računa v primeru, da je pozitiven, nima predznaka. Po drugi strani moramo predznak »-« vedno zapisati. Kadar imamo opravka hkrati s predznakom »+« ali »-« in računsko operacijo »+« ali »-«, velja pravilo, da dva »-« dasta »+« (o, ko bi bilo tako tudi pri ocenjevanju!) :) Predznaka »krat« in »deljeno« pa kot taka ne obstajata, zato se nikoli ne bomo srečali npr. z računom 10:(:5), bomo pa srečali račun npr. 10:(1/5), ki se od prvega praktično ne razlikuje, saj enica pri množenju in deljenju ne spremeni vrednosti računa. In tu se lahko spomnimo pravila »dva minusa dasta plus«, saj analogno tudi »dve deljenji dasta množenje« (matematiki bi nas spet za ušesa :)) in račun 10:(:5) oziroma 10:(1/5) postane 10 · 5. To si velja zapomniti, saj nas analogija pogosto lahko reši iz zadrege, če kaj pozabimo. A pozor – učitelju ne skušajte »prodati« računa 10:(:5), ampak vmes vrinite tisto enico (10:(1/5)), da vas – ne bo za ušesa seveda. :) Več na temo povezav med seštevanjem in odštevanjem oz. med množenjem in deljenjem ter nasprotnih in obratnih vrednostih pa najdete v samostojnem članku. Kdaj lahko »dam vse na eno dolgo ulomkovo črto«? Kadar imamo v računu (ali v delu računa) samo množenje in deljenje ulomkov ter celih števil, lahko vse skupaj zapišemo na eno ulomkovo črto, ki jo po potrebi podaljšamo (če je možno kaj »krajšati« oziroma, bolj pravilno rečeno, poenostaviti). Pri zapisu na »dolgo« ulomkovo črto ulomkov, pred katerimi stoji znak za deljenje, ne pozabimo »obrniti okoli«. Deljenje se v tem primeru spremeni v množenje, tako da ima taka »dolga« ulomkova črta tako v števcu kot v imenovalcu zgolj računsko operacijo množenja, kar nam omogoča enostavno krajšanje. Ali lahko ulomke lahko krajšam »križkraž«? Seveda. In to večkrat. :) Zakaj? Ker imamo tako v imenovalcu kot v števcu račun, ki vsebuje zgolj množenje, za katerega velja zakon o zamenjavi (recimo 3 krat 5 je isto kot 5 krat tri ...) Na spodnji sliki vidimo, da 3 v števcu in 6 v imenovalcu lahko krajšamo s 3, 10 v števcu in 5 v imenovalcu pa z 2, kljub temu, da ne ležijo »eden pod drugim«. 2 v imenovalcu iz prvega krajšanja in 2 v števcu iz drugega krajšanja lahko nato še enkrat krajšamo z 2. Aja, pa še nekaj. Lepše kot »krajšati« se sliši »poenostaviti«, saj po tem postopku ulomek ni nič »krajši«, J ampak zgolj poenostavljen, saj je vrednost okrajšanega ulomka enaka »originalnemu« ulomku. Kdaj je priporočljivo celo število pretvoriti v ulomek in kako to storim? Kadar celo število nastopa "v družbi ulomkov" v računu množenja ali deljenja, ga je najbolj enostavno pretvoriti v ulomek in nato z njim računati tako kot z ulomkom. Na ta način se ne bomo nikoli spraševali, ali ga je potrebno zapisati v števec ali imenovalec ulomka. Celo število v ulomek pretvorimo tako, da ga zapišemo v števec (zgoraj), v imenovalec (spodaj) pa zapišemo vrednost 1. Dokaj logično, če vemo, da ulomek predstavlja deljenje, deljenje z 1 pa na deljenca nima vpliva. Primer: 5=5/1. Če s tem številom množimo, vemo, da gre 5 v števec "dolge ulomkove črte", 1 pa v imenovalec. Če pa z njim delimo, vemo, da ga moramo "obrniti na glavo", zato na "dolgo ulomkovo črto" zapišemo 1 zgoraj, 5 pa spodaj. Če imamo poleg celega števila zraven še ulomek, je tak zapis pri množenju in deljenju potrebno pretvoriti v »nepravi ulomek«. Za več »poskrolajte« malo višje po članku. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Če »gremo kje čez«, nepravi ulomek pretvorimo v pravega, celoštevilski del pa ustrezno povečamo. Če »nam kje zmanjka«, pa si od celega števila »izposodimo« ulomek tipa n/n in odštevanje izvedemo posebej za cela števila in posebej ulomke. Za podrobnejšo razlago »poskrolajte« malo višje po članku. Kdaj je koristno decimalno število pretvoriti v ulomek?
Marsikdo »ne mara ulomkov«, zato v računih, kjer nastopa kombinacija decimalnih števil in ulomkov, slednje vedno pretvori v decimalna števila in se potem »igra s premetavanjem decimalnih vejic«. Poleg tega, da je tako računanje »manj elegantno«, rezultat take pretvorbe ni vedno končno decimalno število, zato ga moramo zaokrožiti, s čimer pa »pridelamo« tudi nekaj pogreška. Zakaj je računanje s pretvorbo ulomkov v decimalna števila »manj elegantno«? Naloge so velikokrat zastavljene tako, da je pri računanju z ulomki »manj pisanja« in veliko faktorjev se »lepo krajša«, tako da tak račun izgleda »lepše« oziroma bolj pregledno. Po drugi strani se pri računanju z decimalnimi števili ni potrebno ukvarjati s pravili za računanje z ulomki, a moramo biti zelo pozorni na decimalne vejice. V računih, kjer nastopa kombinacija decimalnih števil in ulomkov, je decimalno število koristno pretvoriti v ulomek predvsem pri množenju in deljenju z ulomki, medtem ko je pri seštevanju in odštevanju včasih lažje, če naredimo obratno – ulomek pretvorimo v decimalno število, predvsem takrat, kadar je rezultat take pretvorbe končno decimalno število.
0 Comments
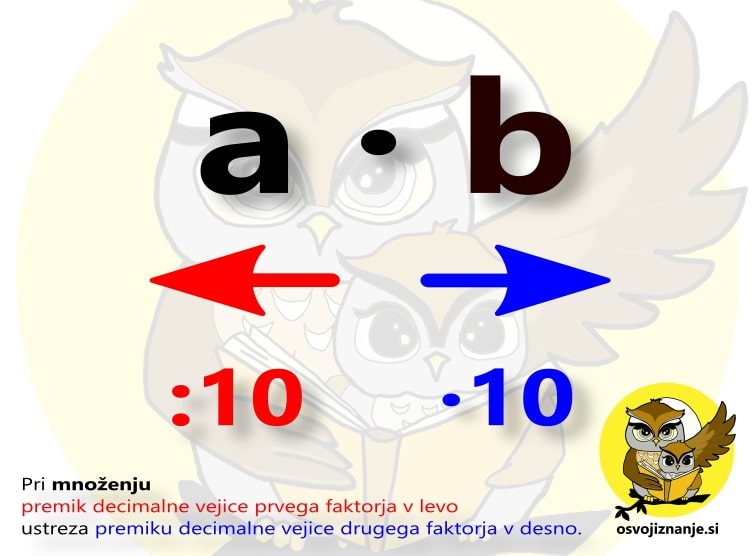
Množenje Množenje dveh števil, od katerih eno vsebuje decimalno vejico, drugo pa je večkratnik desetiške enote (po domače: konča se z ničlami), si lahko poenostavimo s tem, da decimalna mesta in ničle "kompenziramo". Kompenzacija lahko poteka v eno ... ... ali pa v drugo smer: Matematično ozadje je preprosto. Če neko število (v našem primeru produkt a ∙ b) delimo z 10 (premik decimalne vejice v levo) in nato še množimo z 10 (premik decimalne vejice v desno), dobimo seveda isto število. Predstava bo še lažja s pomočjo primera:
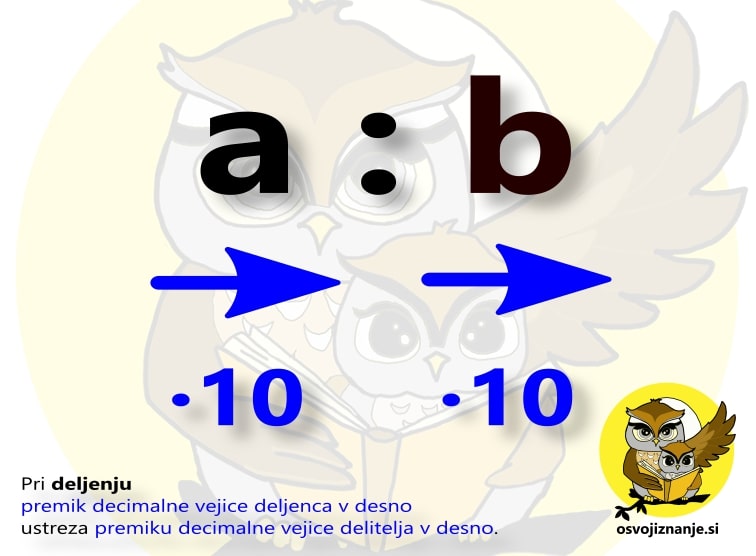
Deljenje Pri deljenju pa se decimalna mesta in ničle za razliko od množenja ne "kompenzirajo" ampak se premik decimalne vejice naredi pri deljencu in delitelju v isto smer. Če deljenec ali/in delitelj vsebuje decimalno vejico, naredimo premik v desno za toliko mest, da sta tako deljenec kot delitelj celi števili: Če ob tem deljencu ali delitelju "zmanjka" decimalnih mest, mu ob vsakem premiku na desno dodamo eno ničlo (več o tem v primerih, ki sledijo). Če pa je deljenec ali/in delitelj večkratnik desetiške enote (po domače: ima na desni strani eno ali več ničel), hkrati odvzamemo obema toliko ničel na desni, da vsaj eden izmed njiju ni več večkratnik desetiške enote (po domače: ima na mestu enic števko, različno od 0): Oglejmo si dva primera. V prvem delimo število 10 z 0,2.
V drugem primeru pa število 600 delimo s 30.
Pri množenju z 10 se decimalna vejica premakne za eno mesto v desno, pri deljenju z 10 pa za eno mesto v levo.
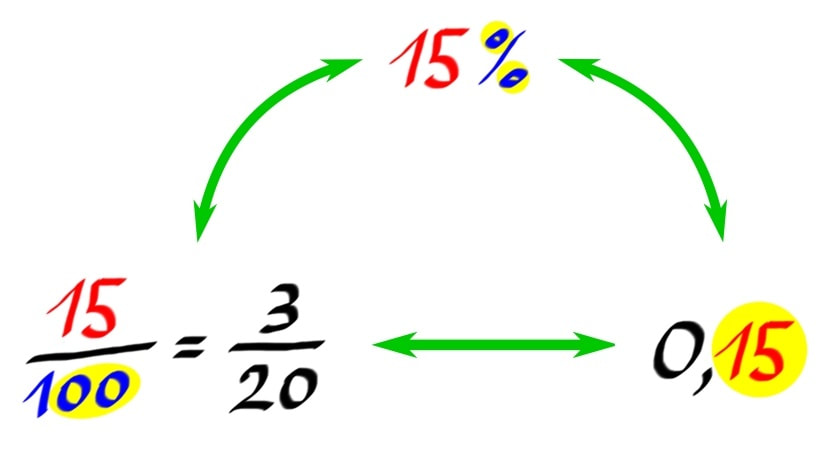
Kako si to najlažje zapomnimo? Preprosto. Premik decimalne vejice v desno pomeni povečanje vrednosti števila, saj ima celi del le-tega več števk, premik decimalne vejice v levo pa zmanjšanje vrednosti števila, saj ima celi del le-tega manj števk. Ker množenje s številom, večjim od 1 pomeni povečanje vrednosti, deljenje pa zmanjšanje le-te, je zadeva dokaj logična :) Število lahko zapišemo v obliki ulomka, decimalnega zapisa ali pa z odstotkom. To še nekako vemo, ko pa je potrebno pretvarjati med zapisi, se pa rado zatakne.
Tukaj je nekaj napotkov:
Preprosto :) in sicer v dveh korakih:
Nekaj primerov:
To najlažje naredimo tako, da delimo števec z imenovalcem, saj ulomek v matematiki pomeni deljenje. Število s končnim decimalnim zapisom (po domače tako decimalno število, ki se ne "vleče" v neskončnost) pa dobimo samo, če ulomek razširimo tako, da v imenovalcu dobimo potenco števila 10 (po domače števila, ki ima spredaj 1, zadaj pa same ničle, npr. 10, 100, 1000,...) V število s končnim decimalnim zapisom lahko pretvorimo ulomek, ki ima v imenovalcu:
V število s končnim decimalnim zapisom pa ne moremo pretvoriti ulomkov, ki imajo v imenovalcu:
Pozor! če imenovalec množimo z nekim številom, moramo seveda z istim številom pomnožiti tudi števec, sicer bomo v godlji! :) Sedaj, ko imamo desetiški ulomek (v imenovalcu je potenca števila 10), le še:
Nekaj primerov:
|
ARHIV
May 2024
KATEGORIJE
All
|

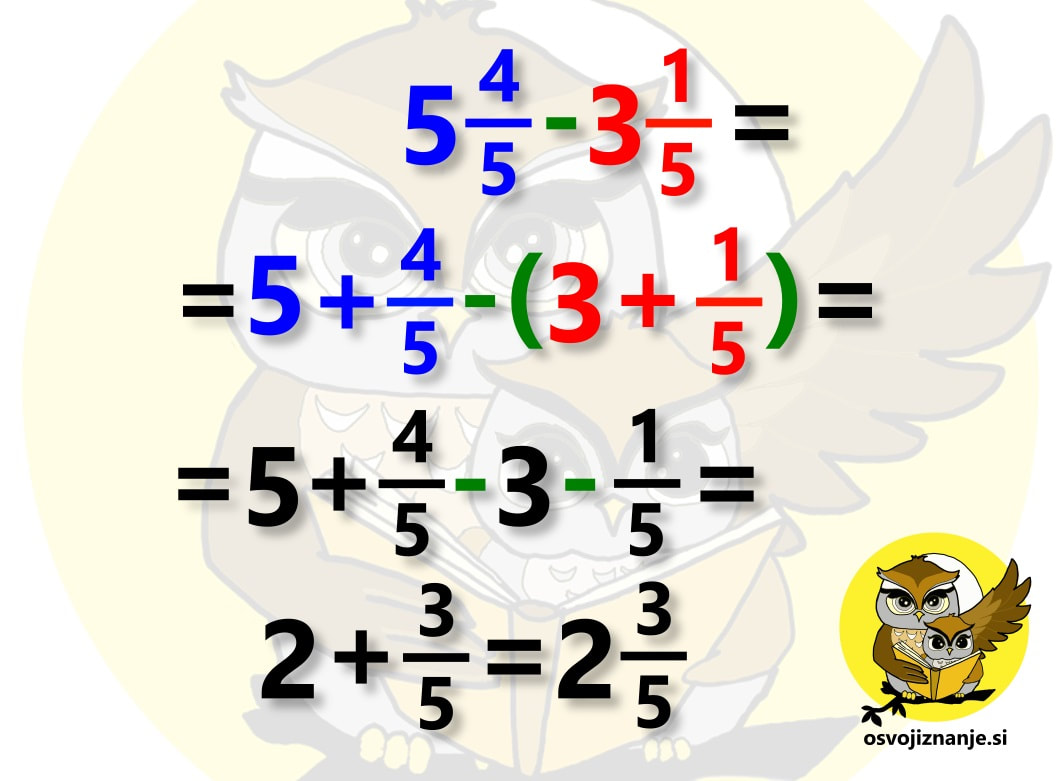








 RSS Feed
RSS Feed
