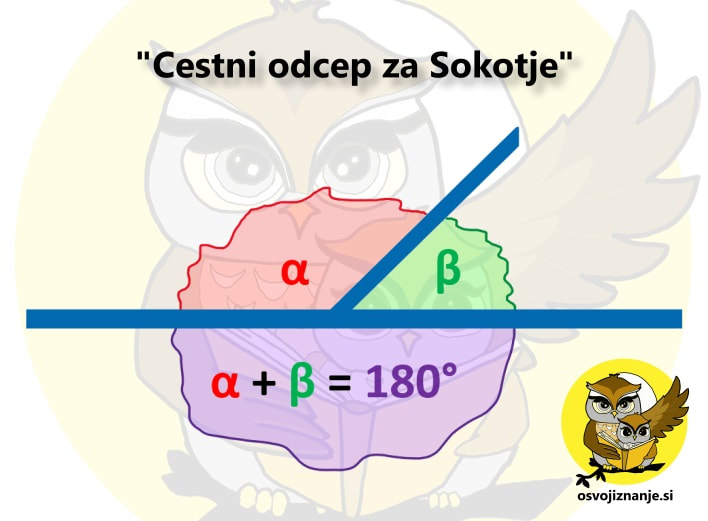
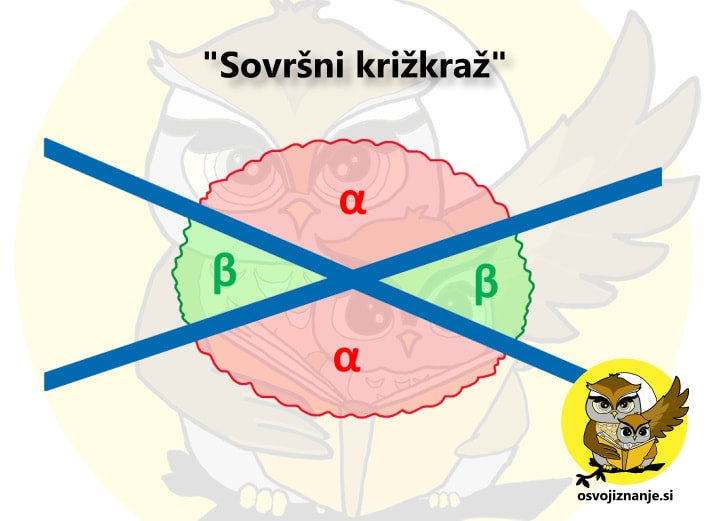
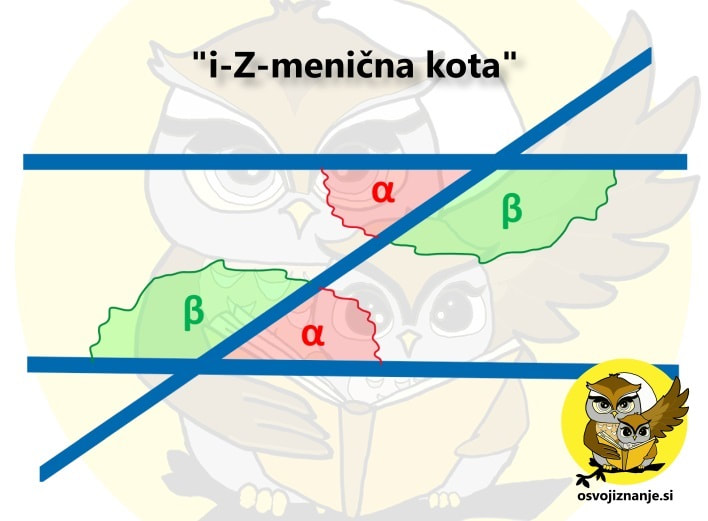
Koti radi nastopajo v paru, tudi v matematičnih testih. ;)

Kdaj sta kota sokota in kdaj sovršna kota? Kaj pa izmenična kota?

Čeprav se sliši zakomplicirano, si pojme zapomnimo veliko lažje, če si jih predstavljamo vizualno, zraven pa pripišemo še kakšno besedno zvezo. Temu se strokovno reče "dvojno kodiranje" (več o metodi učenja si lahko preberete v našem slovarčku).
 
Mi imamo za vas nekaj predlogov, izmislite pa si seveda lahko tudi svoje.
 
Ko govorimo o sokotih, si lahko predstavljamo ravno cesto z odcepom:

Za sokota je značilno tudi to, da si delita en krak. No, ta krak je v našem primeru cestni krak :).
 
Pri učenju sovršnih kotov si lahko predstavljamo »križkraž« ali črko x:

Za sovršna kota je značilno tudi to, da si delita vrh, na kar lahko sklepamo že iz imena samega. Če seveda vemo, kaj je vrh kota. ;) 
 
Tudi tu se lahko znajdemo - če sta kraka nogi, je vrh kota lahko glava (saj se spomnite »glavonožcev«, ki smo jih risali v vrtcu? :)
 
Pri izmeničnih kotih pa si zopet lahko pomagamo z abecedo, to je lahko črka Z ali pa črka N (kot nalašč obe najdemo tudi v imenu - iZmeNična kota):

Ob pozornem pogledu na zadnjo sliko pa lahko opazimo tako sokote kot tudi sovršne kote. Kot je matematiki že običaj, je tudi tu vse povezano med seboj.

Zato kot že mnogokrat - ne učimo se matematike na pamet, ampak - po pameti! ;)

Včasih nam kaj nikakor noče in noče "iti v glavo", zato se je potrebno spomniti kakšne "zvijače". Tu nikakor  nimam v mislih kakšnega nelegalnega početja (plonkanje ...), pretentati je potrebno naše možgane :) Asociacije in kratke zgodbice so kot nalašč za to.

​Premica ne more stati na točki oziroma premica ne more biti element na točki, tako kot se slon ne more usesti na muho :) Zato ne pišimo p ∈ A, ampak A ∈ p.

Kaj dela mimobežnica? Beži mimo krožnice, kajpak :) Kaj pa dotikalnica? Ta se je pa dotika. Sekanta jo pa - seveda - seka.

Kaj je razlika med sekanto in tetivo? Sekanta je ravna nitka, ki seka krožnico, tetivo pa dobimo, ko z ostrim rezilom (krožnico) odrežemo odvečna dela na levi in desni, tako kot pri krpanju nogavic :)

Če imaš pri risanju geometrijskega lika nekje podano le dolžino neke stranice, ne pa tudi njene smeri, uporabi šestilo. Zamisli si, da stojiš na mestu, kamor zapičiš konico šestila, nato pa se z daljnogledom, ki "nese" do točno določene dolžine, ozreš na vse strani okoli sebe. Ni vrag, da v določeni smeri ne ugledaš iskanega cilja ;)

Če imaš pri risanju geometrijskega lika podano višino, nariši cesto, katere širina je enaka višini.

Pri risanju geometrijskega lika išči podatke, ki se "tiščijo skupaj". Zadeve bodo najbolj "pod kontrolo", če začneš pri podatku, ki je "v zlati sredini" :)

Deljenje. Za nekoga "u izi, navadn", za drugega nočna mora.

Najlažje je, če si ga predstavljamo "v živo". Ko ga enkrat dojamemo, je res povsem "simpl" :)

Prva težava se ponavadi pojavi že pri samih izrazih. Zakaj neki​ deljenec, delitelj in količnik? Imajo mogoče koliščarji kaj tu zraven??

Vam je zdaj kaj bolj jasno? Vidite, da koliščarjev res ni bilo zraven :)

Ostanimo še nekoliko pri enakih delih. Veste, da si z deljenjem lahko pomagamo pri delitvi pravokotnika na enake dele? Če smo povsem iskreni, gredo tu zasluge bolj množenju, obratni operaciji deljenja. Aja, pa ulomek je isto kot deljenje, če ste slučajno pozabili ;)

Za lažjo predstavo si oglejte še našo igro "Matematični osvajalci".

No, pa razložimo tole zgodbico lepo in počasi :)

Enkrat je bila ena premica. Ime je dobila po tem, ker je bila revica vsa prema (po SSKJ: prema = ravna). Bila je svobodna. Segala je v eno in drugo smer v neskončnost.

Potem pa je prišla od neznano kje ena točka in se je usedla nanjo, tako grdo, da jo je kar razpolovila. Na njenem mestu sta nastala dva poltraka, a nobeden od njiju ni bil povsem svoboden. V neskončnost sta se raztezala le v eno smer, medtem ko ju je na drugi strani omejevala - kdo drug kot grozna točka.

Naša premica je pa imela sorodnico, ki se ji je pripetila nekoliko drugačna prigoda. Točke so imele prvenstvo v padalskih skokih. Med tekmovalkami sta bili tudi točka A in točka B. Sicer sta želeli pristati na isto mesto, a jima ni uspelo, tako da je bila med njima kar precejšnja razdalja. Omenjeno situacijo je slikal fotograf, ki je bil slučajno matematik in je sklenil, da bo del premice med točkama A in B poimenoval kar daljica. In še danes je tako.

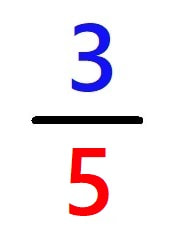
Distributivnost oziroma zakon o razčlenjevanju je lastnost množenja, da se lahko faktorji razčlenijo in posamezni členi teh faktorjev množijo.

Verjetno vam je zgornji stavek popolnoma jasen. Ne? Itak :)

Razložimo pojem bolj “po domače”.

Verjetno vas je večina že videla kakšen napovednik za prihajajoči film. Na koncu napovednika je običajno omenjen tudi distributer (npr. “Distribucija Karantanija Cinemas”). In kaj počne distributer? Distribuira filme, seveda :) No, da se ne boste izgubili med tujkami, najprej razložimo, kaj ta beseda sploh pomeni.

Po SSKJ distribucija pomeni razdeljevanje oz. razpošiljanje. Distributerji pa razdeljujejo, razpošiljajo… Filmski distributer razpošilja filme kinooperaterjem, obstajajo pa tudi drugi distributerji, recimo distributer plina, električne energije, bencina, prehrambenih izdelkov itd.

In kakšno zvezo ima filmska industrija z matematiko? Če ne drugega, oboji poznajo pojem distributivnost :) Če distributer distribuira, je distributivnost sama sposobnost distribucije. Joj, kakšen stavek! :) Preden vse skupaj do konca zavozlamo, si poglejmo praktičen primer.
​
Zamislimo si, da ima filmski distributer na mizi en kup filmskih kolutov, ki jih mora razposlati različnim kino operaterjem:

Najprej jih podolgem in počez razdeli (glej črte na spodnji sliki), nato pa razpošlje. Nekaj v Kolosej, nekaj v Cineplex in tako naprej. Vsak kinooperater ima svojo barvo kolutov:

In kje je tu distributivnost? Oglejmo si primer še z matematične plati.

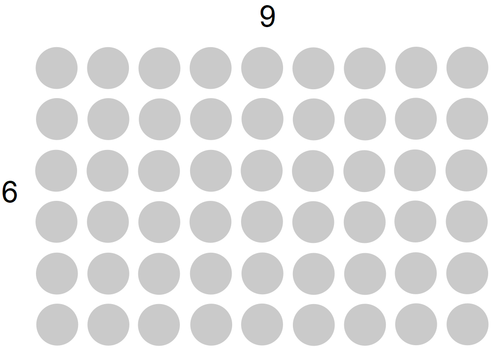
Iz prve slike s pomočjo znanja poštevanke hitro ugotovimo, da je kolutov 9•6, torej 54.

Na drugi sliki pa so naslednji koluti:

• 1•2=2 modra,
• 1•3=3 rdeči,
• 1•4=4 zeleni,
• 5•2=10 rumenih,
• 5•3=15 oranžnih in
• 5•4=20 roza.

Ker gre za iste kolute kot na prvi sliki, bi po logiki tudi teh moralo biti 54. S preprostim seštevanjem različnih barv ugotovimo, da naša trditev drži:

2 + 3 + 4 + 10 + 15 + 20 = 54

Vse lepo in prav, ampak še vedno ne vemo, kje je tu distributivnost. No, sedaj pa si že res zaslužite odgovor :)

V računu za prvo sliko (sivi koluti) imamo dva faktorja: 9 in 6.

Ker je množenje distributivno, lahko katerega koli od faktorjev razčlenimo na poljubno število členov (pretiravat pa vseeno ni treba). Mi smo razčlenili kar oba faktorja (glej drugo sliko): 

• 9 smo z navpičnima črtama razčlenili na 2, 3 in 4
• 6 pa smo z vodoravno črto razčlenili na 1 in 5.

Račun 9•6 je tako postal (2+3+4)(1+5).

Distributivnost oziroma zakon o razčlenjevanju nadalje pravi, da je sedaj potrebno posamezne člene zmnožiti med seboj. Saj poznate tisto: “Množimo vsakega z vsakim!” Naš račun se tako glasi:

9•6 = (2+3+4)(1+5) = 1•2 + 1•3 + 1•4 + 5•2 + 5•3 + 5•4 = 2 + 3 + 4 + 10 + 15 + 20 = 54

Mogoče se tole komu zdi brez veze, češ kaj pa kompliciramo, saj bi z znanjem osnovnošolske poštevanke enostavno zmnožili 9 in 6 ter dobili rezultat 54. V bistvu ni brez veze, le primer je nekoliko prelahek. Ampak saj primeri morajo biti lahki, da jih razumemo.

Poglejmo si še en primer. Zmnožimo števili 15 in 18. Tega se pa niste učili v osnovni šoli, ane? :)

S pomočjo distributivnosti račun 15•18 lahko preoblikujemo na raven osnovnošolske poštevanke, začinjene z nekaj seštevanja:

15•18 = (10+5)(10+8) = 10•10 + 10•8 + 5•10 + 5•8 = 100 + 80 + 50 + 40 = 270

Pa ne recite: "Ah, sej 'mamo kalkulator!" Možgančke je fino malo peljati na sprehod, da se ne zasedijo ;)