|
Od kod izvira poimenovanje za "racionalna števila"?
Ne, izraz nima zveze z razumom ali premišljenostjo (razlaga v SSKJ), čeprav pri matematiki to pride še kako prav, :) ampak izvirajo iz drugega pomena latinskega izraza ratio, ki pomeni računanje, delo s števili, izvajanje postopka ... V angleščini "ratio" pomeni razmerje, ta beseda pa se skriva tudi v definiciji racionalnih števil, saj gre za števila, ki jih lahko izrazimo kot razmerje dveh celih števil. Za "firbčne" je tule še nekaj povezav:
0 Comments
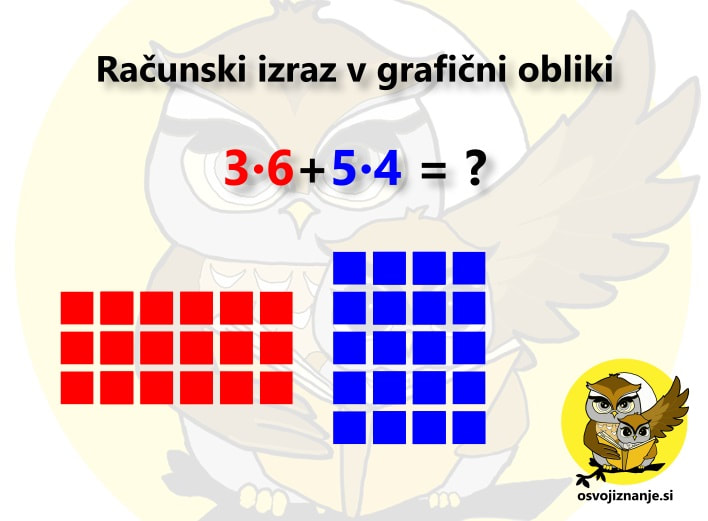
Marsikdo si težko zapomni, da ima množenje (in deljenje) prednost pred seštevanjem (in odštevanjem). Predstavljajmo si, da se v testu pojavi račun 3∙6+5∙4. Ker smo itak živčni, pozabimo katera računska operacija ima prednost. Seštevanje ali množenje? Iz zagate nas reši grafični model računa: Če izraz zapišemo (ali pa si ga zgolj predstavljamo) v grafični obliki (v našem primeru 3 vrste po 6 in 4 vrste po 5), vidimo, da vse elemente (npr. kvadratke) preštejemo tako, da najprej izračunamo polji (računa na krat), nato pa vse skupaj še seštejemo.
Za konec pa še izziv za vas. Kako bi grafično predstavili račun 8∙7-6∙5? Kaj pa 9∙5-6∙7? (V prvem primeru kvadratke modrega pravokotnika dimenzij 6∙5 položimo na rdeči pravokotnika dimenzij 8∙7. Preostanek rdečega pravokotnika je rezultat. V drugemprimeru storimo enako, le da je potrebno kvadratke modrega pravokotnika nekoliko preoblikovati, da "pašejo" na rdeč pravokotnik.) »Hm«, boste rekli, »a nismo v šoli rekli, da velja zgolj za seštevanje in množenje? Ja. In ne. :) Če odštevanje obravnavamo strogo kot odštevanje in deljenje kot deljenje, potem ne moremo splošno reči, da zanju velja zakon o zamenjavi. Če pa:
A pozor! Računsko operacijo pred številom, ki ga želimo »nesti drugam«, moramo v tem primeru »vzeti s seboj«! Oglejmo si dva primera. V prvem želimo odštevanje postaviti na konec računa, da ga bomo izvedli nazadnje. To lahko storimo, a ne pozabimo minusa pred številom 5! V drugem primeru pa želimo deljenje izvesti prej, da ne bo deljenec prevelik. Število 4 lahko postavimo takoj za 12, a ne pozabimo »s seboj nesti« tudi znaka za računsko operacijo deljenja! Da me ne boste "prijeli za besedo": V matematičnem členu po Wikipediji v členu lahko nastopata zgolj številski operaciji množenja in potenciranja. Kaj pa deljenje? Če si deljenje z nekim številom (v našem primeru s 4) predstavljamo kot množenje z ulomkom, ki ima to število v imenovalcu, števec pa enak 1 (v našem primeru 1/4), pa imamo čisto pravi člen s štirimi faktorji: 12, 2, 3 in 1/4.
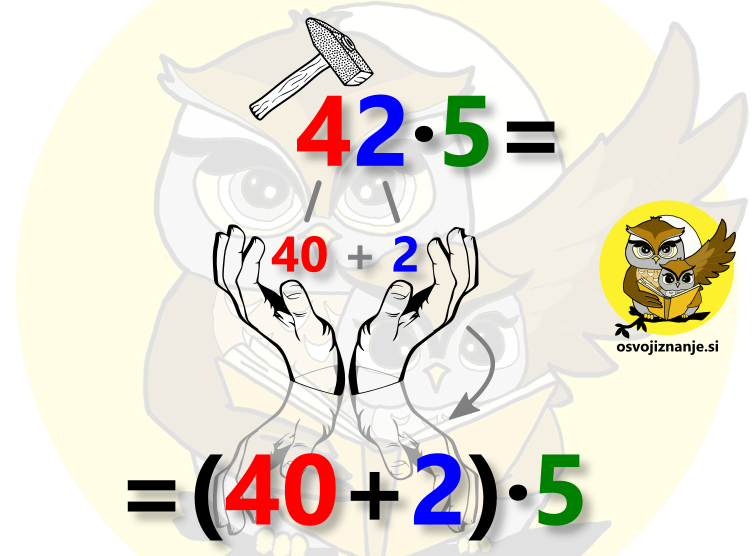
O tem, kaj je distributivnost, lahko nekaj več preberete tule, mi pa si poglejmo kar primer. Izračunajmo račun 42 krat 5. Poštevanka nam tu direktno ne more pomagati, saj jo znamo le do 10 krat 10, si pa lahko pomagamo tako, da razdelimo prvi faktor na dva dela (42 razdelimo na štiri desetice in dve enici), katera potem ločeno množimo z drugim faktorjem (v našem primeru 5) in na koncu seštejemo (po distributivnostnem zakonu). Da bo vse skupaj še lažje, si izmislimo zgodbico. 🙂 Recimo, da s kladivom udarimo po večjem od števil (42), nakar to razpade v števili 40 in 2, ki ju ujamemo v roko in postavimo v oklepaj: Števil ni nujno drobiti na vrednosti pod 10, saj poštevanka zajema celoštevilske faktorje do vrednosti 10. Močno si lahko pomagamo že z razčlenitvijo na večkratnike desetiških enot. Mi smo število 42 s tem namenom razdelili na 40 (4 krat 10) in 2. Namesto množenja števil 42 in 5 bomo tako s 5 zmnožili števili 40 in 2 ločeno, rezultata množenja pa na koncu sešteli. Nadaljujmo našo zgodbico od včeraj. 😉 Petico si na primer predstavljajmo kot psa, na katerega z vsake številke v oklepaju skoči ena bolha. Vsak skok pomeni eno množenje. Prvo je 40 krat 5, drugo pa 2 krat 5: Sedaj moramo izračunati le še preprost računski izraz (ne pozabimo, da ima množenje prednost pred seštevanjem) in smo končali. 🙂 Za tak način množenja torej potrebujemo le znanje poštevanke, seštevanja in množenja z večkratniki potenc števila 10. Zakaj iz 4 ∙ 5 = 20 sledi, da je 40 ∙ 5 = 200? Preprosto. 40 ∙ 5 lahko zapišemo tudi kot 4 ∙ 10 ∙ 5 oziroma 4 ∙ 5 ∙ 10 (zakon o zamenjavi) oziroma 20 ∙ 10 (zakon o združevanju), pri množenju z 10 pa vemo, da v rezultatu "pridelamo" dodatno ničlo na desni strani (oziroma premik decimalne vejice v desno, kadar računamo z decimalnimi števili).
Na koncu še vprašanje za vas. V našem primeru smo delna zmnožka na koncu sešteli. Pri katerih številih, recimo dvomestnih, pa bi bil račun lažji, če bi uporabili odštevanje? (Kadar je enica večja od 5, npr. pri računu 48 ∙ 5.) |
ARHIV
May 2024
KATEGORIJE
All
|


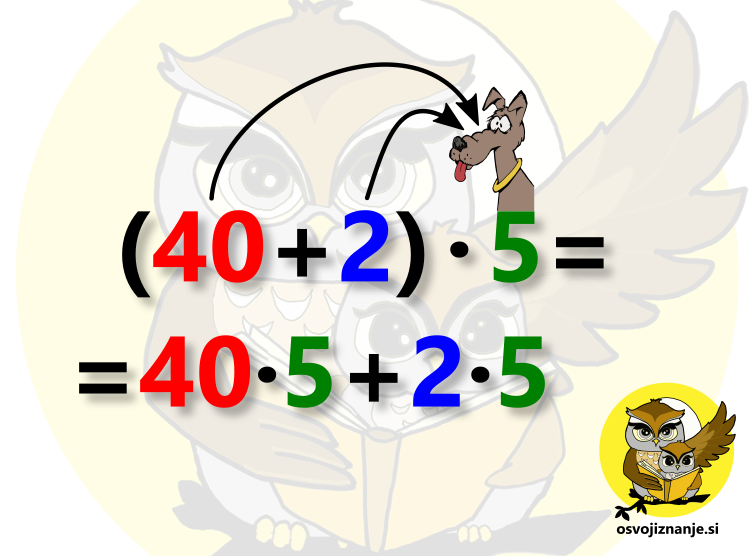
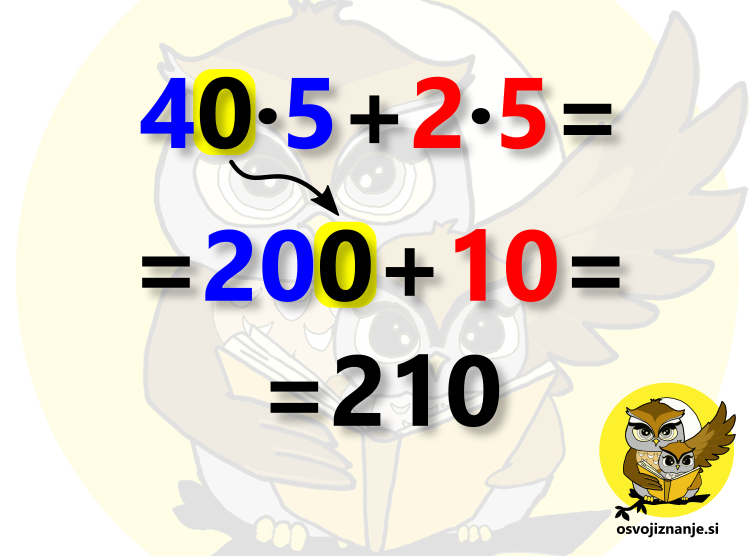
 RSS Feed
RSS Feed
