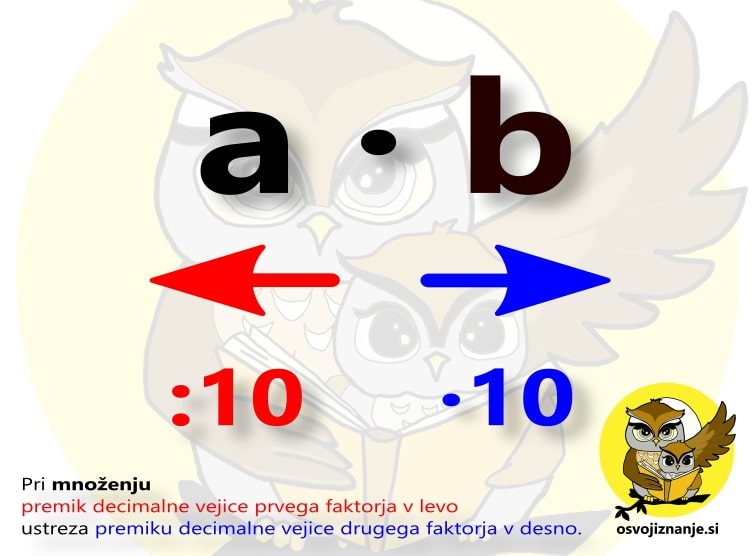
Množenje

Množenje dveh števil, od katerih eno vsebuje decimalno vejico, drugo pa je večkratnik desetiške enote (po domače: konča se z ničlami), si lahko poenostavimo s tem, da decimalna mesta in ničle "kompenziramo".

Kompenzacija lahko poteka v eno  ...

Matematično ozadje je preprosto. Če neko število (v našem primeru produkt a ∙ b) delimo z 10 (premik decimalne vejice v levo) in nato še množimo z 10 (premik decimalne vejice v desno), dobimo seveda isto število.

Predstava bo še lažja s pomočjo primera:

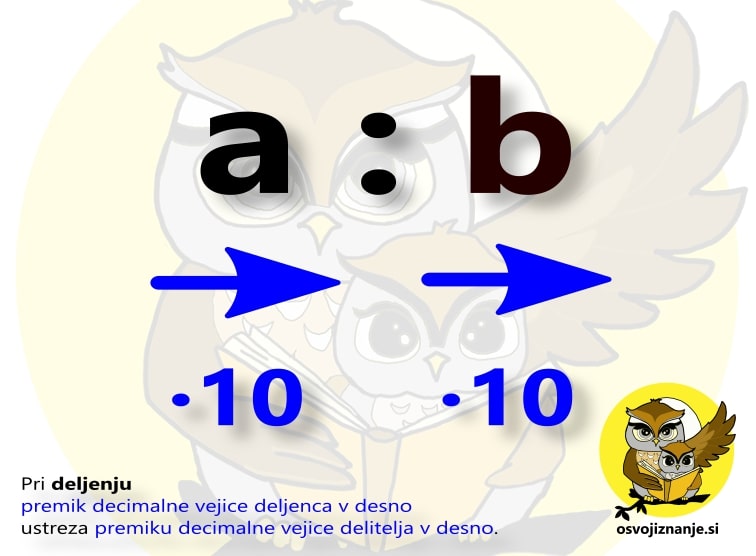
• Zmnožimo števili 2,5 in 400. Prvi faktor vsebuje eno decimalno mesto, drugi pa je večkratnik stotice (konča se z dvema ničlama).
• "Kompenziramo" eno decimalno mesto prvega faktorja z eno ničlo drugega faktorja in dobimo račun 25 ∙ 40.
• Po zakonu o (raz)druževanju račun lahko zapišemo kot 25 ∙ 4 ∙ 10 oziroma (25 ∙ 4) ∙ 10. 
• Izračunamo 25 ∙ 4 = 100, na koncu pa upoštevamo še pravilo za množenje s potencami števila 10 in dodamo rezultatu še eno ničlo na desno.​

Če ob tem deljencu ali delitelju "zmanjka" decimalnih mest, mu ob vsakem premiku na desno dodamo eno ničlo (več o tem v primerih, ki sledijo).

Če pa je deljenec ali/in delitelj večkratnik desetiške enote (po domače: ima na desni strani eno ali več ničel), hkrati odvzamemo obema toliko ničel na desni, da vsaj eden izmed njiju ni več  večkratnik desetiške enote (po domače: ima na mestu enic števko, različno od 0):​

​Oglejmo si dva primera.

V prvem delimo število 10 z 0,2.

• Deljenec se konča z ničlo, delitelj pa vsebuje eno decimalno mesto. 
• Ker delitelj vsebuje decimalno vejico, naredimo premik v desno za toliko mest, da sta tako deljenec kot delitelj celi števili. V našem primeru decimalno vejico premaknemo za eno mesto v desno in dobimo račun 100 : 2.

Glede na to, da je ena izmed interpretacij ulomkov razmerje, bi ulomke lahko krajšali in razširjali oziroma pretvarjali na določeni števec ali imenovalec tudi s tabelo razmerij (angl. ratio table).

Preden si ogledamo nekaj primerov, najprej razmislek v povezavi z izrazoma krajšanje in razširjanje ulomkov. Pam Harris, predavateljica na Teksaški univerzi, avtorica številnih knjig in promotorka poučevanja t.i. »prave matematike« (angl. »real math«) me je opozorila, da je primernejši izraz za hkratno deljenje števca in imenovalca z istim številom poenostavljanje, saj vrednost ulomka po »krajšanju« ni nič manjša kot prej.

Tudi »razširjanje ulomka« bi bilo po tej analogiji bolje imenovati pretvorba ulomka na določeno vrednost števca oz. imenovalca.

Primer 1: poenostavi ulomek  180/300:

Števec in imenovalec smo trikrat podvojili (množenje ulomka z 2), nato pa sešteli vrednosti v prvem in četrtem stolpcu s številkami (2+16=18, 3+24=27). Pozor! Tu ne gre za seštevanje ulomkov 2/3 in 16/24! Pomislimo na reševanje sistemov enačb (metoda nasprotnih koeficientov) ...

Pri takem sklepanju se osredotočimo na števec, a ne pozabimo na imenovalec!

Primer 3: pretvori ulomek na vrednost imenovalca 100:

Števec in imenovalec smo podvojili, nato pa smo ju pomnožili še z 10.

​Pri takem sklepanju se osredotočimo na imenovalec, a ne pozabimo na števec!

Za konec pa še odgovor na vprašanje: »Zakaj je pretvarjanje ulomkov sploh potrebno?« V tem najdemo vsaj dva smisla. Zakaj poenostavljamo, nam pove že samo ime – zato, da je ulomek enostavneje zapisati, ga prebrati, si ga zapomniti ... Pretvarjanje na določeno vrednost imenovalca, točneje na potence števila 10, pa nam pomaga pri pretvorbi ulomka v decimalno število ali odstotek. Smisla pretvarjanja na določeno vrednost števca pa do danes še nisem našel, čeprav v učbenikih najdemo tudi take naloge. :)