|
V računskih izrazih poznamo dve osnovni postavitvi oklepajev:
Zaporedna oklepaja lahko razrešujemo istočasno (v isti vrstici izraza), medtem ko pri vgnezdenih oklepajih začnemo z reševanjem v notranjosti, nakar se pomikamo navzven. Primera z zaporednimi oklepaji:
Primera z vgnezdenimi oklepaji:
0 Comments
Za razliko od "rumenega" in "oranžnega" pravila zeleno pravilo uporabljamo samo pri računanju izrazov v algebri (črke in številke) in sicer pri poenostavljanju končnega izraza ("kače" členov, ki nam ostane potem, ko smo že razrešili oklepaje ter vse potrebno potencirali, korenili, zmnožili in delili) Pri rumenem pravilu seštevanja in odštevanja smo omenili, da v algebri podobne člene seštevamo / odštevamo ločeno ("hrušk in jabolk" seveda ne moremo seštevati :) ). Zeleno pravilo se glasi:
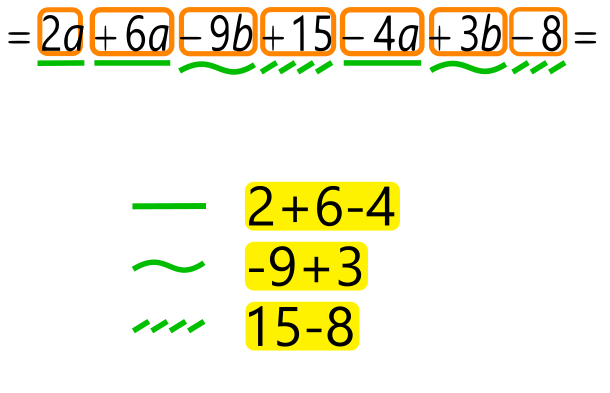
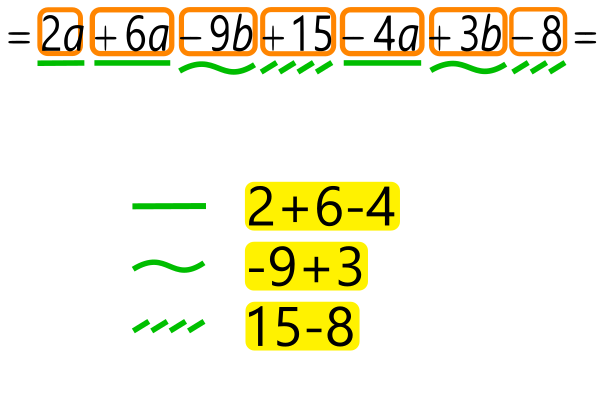
Pomni! Podobni členi so tisti členi, ki imajo različne številske faktorje in enake spremenljivke (na primer 4bc in -3bc). Enaki členi pa imajo enake tako številske faktorje kot tudi spremenljivke. Če odštejemo enaka člena, dobimo 0. Primer končne "kače" členov; členi so obkroženi z oranžno barvo in nato grupirani po zelenem pravilu. Znotraj vsake "zelene" skupine je uporabljeno rumeno pravilo; ravna črta so a-ji, vijugasta b-ji, poševno črtkana črta pa predstavlja številske člene.
Rumeno pravilo" seštevanja in odštevanja že poznamo, za naziv "mojster reševanja matematičnih izrazov" pa moramo spoznati še t.i. oranžno pravilo množenja in deljenja. Kot vemo, so seštevanje, odštevanje, množenje in deljenje osnovne matematične operacije. Vemo tudi, da imata množenje in deljenje v računskih izrazih prednost pred seštevanjem in odštevanjem. "Oranžno pravilo" bo imelo torej prednost pred "rumenim". Pravilo množenja in deljenja uporabimo pri:
Za množenje oziroma deljenje dveh členov se pravilo glasi:
Oglejmo si ga še v grafični obliki (več o pomenu krožcev si lahko ogledate v članku o računanju s simboli): Pomni! Situacijo, ko je pred oklepajem samo minus, upoštevamo kot množenje (-1) s členi v oklepaju, torej se vsem členom v oklepaju zamenja predznak! V primeru več členov pa pravilo lahko posplošimo:
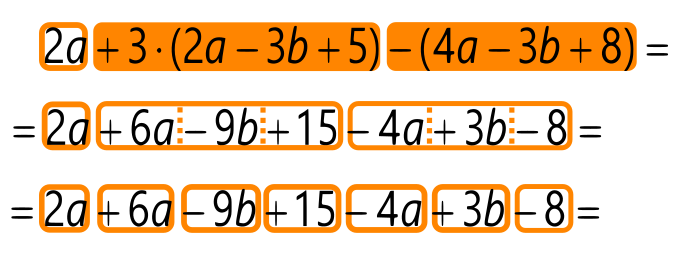
Pomni! Potenciranje števila upoštevamo kot množenje števila s samim seboj (tolikokrat, kolikor je vrednost eksponenta); v primeru potenciranja negativnega števila (minus je znotraj oklepaja, na primer (-5)²) je zato končni predznak odvisen od tega, ali je eksponent liho ali sodo število! Potenciranje posameznega števila vedno izvedemo pred množenjem z ostalimi faktorji znotraj posameznega člena! V izrazu 3⋅(-3)² recimo najprej izračunamo (-3)²=9 in nato šele 3⋅9=27. V istem koraku kot potenciranje izvedemo tudi korenjenje, a zanj oranžnega pravila ne uporabljamo. Ideja: Člen, znotraj katerega bomo uporabili oranžno pravilo, lahko obkrožimo z oranžno in ga pobarvamo. Po uporabi oranžnega pravila nastanejo novi členi, katere le obkrožimo z oranžno barvo. Z oranžno barvo lahko obkrožimo tudi ostale člene, kjer oranžnega pravila ni potrebno uporabiti. Tako dobimo pregleden "zemljevid" členov, ki jih bomo potrebovali za končen izračun po rumenem (aritmetika - samo številke) oziroma zelenem in rumenem (algebra - številke in črke) pravilu. Primer uporabe oranžnega pravila v aritmetičnem izrazu Primer uporabe oranžnega pravila v algebrskem izrazu
"Kakšno pravilo pa je že spet to?" boste nemara pripomnili. Brez panike, to pravilo ni le še ena kaplja v morju pravil, med katerimi se ne znajdete več. Da bi vam olajšali pot iz matematične zagate, smo za vas pripravili nekaj temeljnih pravil za računanje. In jih poimenovali kar po barvah, česar boste veseli predvsem "vizualni tipi". Vsako izmed pravil bomo predstavili posebej, potem pa se bomo nanje po potrebi sklicevali. Videli boste, da teh pravil niti ni toliko, kot si mislimo. Vsaj ne osnovnih. Kar nakazuje, da matematika res ni tako težka, kot se zdi na prvi pogled :) Začnimo z najosnovnejšim pravilom računanja, pravilom o seštevanju in odštevanju. Pravilo seštevanja in odštevanja uporabimo pri:
Pravilo se glasi:
Pri računanju si lahko pomagamo tudi s tabelo. Pozor! V algebri (številke in črke) podobne člene seštevamo / odštevamo ločeno, saj "hrušk in jabolk" seveda ne moremo seštevati :). Ideja (aritmetika - samo številke): Števila, na katerih bomo uporabili rumeno pravilo, lahko obkrožimo z rumeno in jih pobarvamo. Primeri uporabe rumenega pravila v aritmetičnem računskem izrazu Ideja (algebra - številke in črke): Na koncu računa, ko imamo le še "kačo" členov, vsak člen obkrožimo z oranžno barvo, pod členi pa z zeleno barvo označimo posamezne podobne člene (ravna črta, vijugasta črta, poševno črtkana črta, ...) Tako dobimo pregleden "zemljevid" podobnih členov, ki nam bo olajšal končen izračun po rumenem pravilu z upoštevanjem grupiranja podobnih členov (zeleno pravilo). Primer končne "kače" členov; členi so obkroženi z oranžno barvo in nato grupirani po zelenem pravilu. Znotraj vsake "zelene" skupine je uporabljeno rumeno pravilo; ravna črta so a-ji, vijugasta b-ji, poševno črtkana črta pa predstavlja številske člene.
Lepota matematike je (med drugim) tudi v tem, da se je marsikaj potrebno naučiti samo na pol12/8/2018 V matematiki najdemo veliko računskih operacij, ki so med seboj obratne. To pomeni, da rezultat prve operacije z drugo operacijo vrnemo nazaj v začetno stanje. Vsakdo od vas bi si verjetno želel matematične operacije, ki bi vašo razmetano sobo pospravila nazaj v "pospravljeno stanje" ;)
"In kje je sedaj tisti del, ki pravi, da se je potrebno naučiti samo na pol?" boste dejali. Če sta računski operaciji obratni, je dovolj, da se določenega postopka naučimo le za prvo, za drugo pa vemo, da omenjeni postopek "obrne na glavo". Oglejmo si primer. Množenje in deljenje sta obratni računski operaciji. Če vemo, da vsako množenje z 10 rezultatu doda ničlo (oziroma decimalno mesto premakne v desno), jo bo vsako deljenje z 10 odvzelo (oziroma decimalno mesto premaknilo v levo). Naštejmo nekaj najbolj pogosto uporabljanih računskih operacij, ki so med seboj obratne:
Oglejmo si še en primer za potenciranje in korenjenje, konkretno za kvadrat in kvadratni koren:
Včasih dve obratni računski operaciji najdemo kar v enem računu, česar se še posebej razveselimo, saj ena operacija izniči drugo, tako da nam sploh ni potrebno ničesar računati :) Oglejmo si nekaj primerov:
Ste vedeli, da se je tudi poštevanke dovolj naučiti le na pol? Za to pa ima zaslugo zakon o zamenjavi, ki velja za množenje. 3·4 je tako enako 4·3 in tako naprej ... Zakon o zamenjavi velja tudi za seštevanje. Načeloma račune z oklepaji štejemo med težje račune. A brez panike, oklepaji niso nič strašnega. Tu so zato, da nam pomagajo.
Razdelimo jih lahko v dve skupini:
Prvi določajo vrstni red računskih operacij v izrazu (oklepaje razrešujemo najprej, nato sledita množenje in deljenje, na koncu pa seštevanje in odštevanje). Primer 1:
Oklepaji v drugi skupini pa preprečujejo zaporeden zapis matematičnih operacij in so nekakšna "zaščita" negativnih členov. Primer 2:
Pogosto se zgodi, da se v računskem izrazu ena vrsta oklepaja preoblikuje v drugo. Primer 3:
Tako oklepaj iz prve kot tudi iz druge skupine se lahko pojavi v kombinaciji z eksponentom. V takih primerih moramo biti še posebej pazljivi, saj:
Primer 4:
Primer 5:
Pomembno! Za razliko od eksponenta pri korenu uporaba dodatnega oklepaja ni potrebna - koren se upošteva vedno za celoten izraz, ki se "skriva pod njim"! V aritmetiki (samo številke) matematični izraz v oklepaju iz prve skupine običajno izračunamo, medtem ko ga v algebri (številke + črke) ne moremo (hrušk in jabolk pač ne moreš enostavno sešteti ;)), zato v okviru algebre srečamo tudi različne kombinacije oklepajev iz prve in/ali druge skupine. Sem spada:
Primer 6:
|
ARHIV
May 2024
KATEGORIJE
All
|

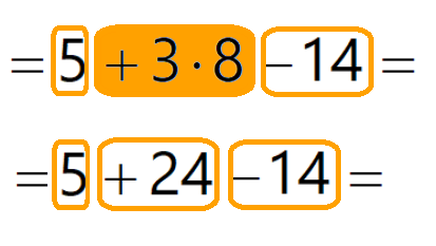
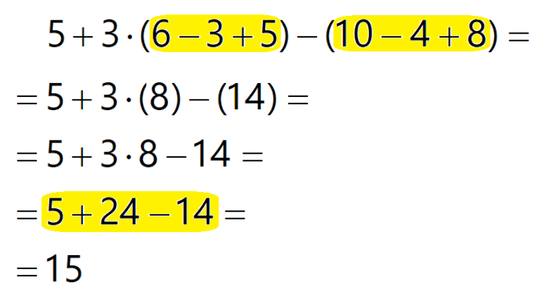
 RSS Feed
RSS Feed
