|
Včasih nam kaj nikakor noče in noče "iti v glavo", zato se je potrebno spomniti kakšne "zvijače". Tu nikakor nimam v mislih kakšnega nelegalnega početja (plonkanje ...), pretentati je potrebno naše možgane :) Asociacije in kratke zgodbice so kot nalašč za to.
Premica ne more stati na točki oziroma premica ne more biti element na točki, tako kot se slon ne more usesti na muho :) Zato ne pišimo p ∈ A, ampak A ∈ p. Kaj dela mimobežnica? Beži mimo krožnice, kajpak :) Kaj pa dotikalnica? Ta se je pa dotika. Sekanta jo pa - seveda - seka. Kaj je razlika med sekanto in tetivo? Sekanta je ravna nitka, ki seka krožnico, tetivo pa dobimo, ko z ostrim rezilom (krožnico) odrežemo odvečna dela na levi in desni, tako kot pri krpanju nogavic :) Če imaš pri risanju geometrijskega lika nekje podano le dolžino neke stranice, ne pa tudi njene smeri, uporabi šestilo. Zamisli si, da stojiš na mestu, kamor zapičiš konico šestila, nato pa se z daljnogledom, ki "nese" do točno določene dolžine, ozreš na vse strani okoli sebe. Ni vrag, da v določeni smeri ne ugledaš iskanega cilja ;) Če imaš pri risanju geometrijskega lika podano višino, nariši cesto, katere širina je enaka višini. Pri risanju geometrijskega lika išči podatke, ki se "tiščijo skupaj". Zadeve bodo najbolj "pod kontrolo", če začneš pri podatku, ki je "v zlati sredini" :)
0 Comments
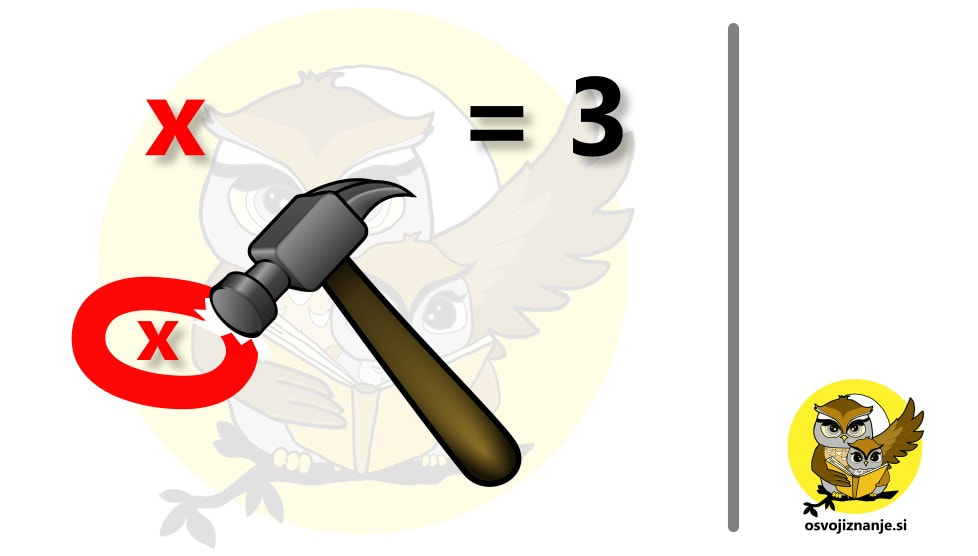
Prav ste slišali, kar s kladivom se je bomo lotili - metaforično seveda :) Omenjen pristop oziroma način razmišljanja utegne koristiti pri enačbah, ki vsebujejo "mešanico" osnovnih računskih operacij - vsaj eno seštevanje oziroma odštevanje ter vsaj eno množenje oziroma deljenje. Tak primer je recimo naslednja enačba: 3x + 2 - 6 = 5 Bistvo vsake enačbe je, da izrazimo oziroma "osvobodimo" neznanko, v našem primeru x. Če imamo preprosto enačbo, ki vsebuje le seštevanje in/ali odštevanje, preprosto uravnovesimo levo in desno stran tako, da bo na eni strani ostala le še neznanka. V našem primeru pa je neznanka pomnožena s faktorjem 3, zato bo potrebno za njeno "osvoboditev" nekoliko več napora. Osredotočimo se stran, ki vsebuje enačbo, v našem primeru na levo. Predstavljajmo si, da je ta izraz veriga: Naša veriga vsebuje 3 člene in kot nalašč, se tudi deli izraza na levi imenujejo členi. Po domače povedano, so členi "gmote" črk in/ali števil, ki so med seboj povezane s plusi in minusi. Več o členih si lahko preberete tule. Členi verige, ki ne vsebujejo iskane spremenljivke, so krhki in bodo odpadli najprej. Enačbo bomo rešili s postopkom istočasnega izvajanja računskih operacij na obeh straneh enačbe hkrati, ki je še najbolj pravilen način reševanja (t.i. "metanja" čez enačaj matematiki ne marajo preveč :) ). Pri tem si bomo pomagali z navpično črto na desni strani zvezka. Kar bomo pisali desno od te črte, si lahko predstavljamo kot komentar, ki nam bo prišel prav, ko bomo čez čas pregledovali svoje zapiske. Komentiranje je zelo razširjeno pri programiranju, še posebej, če programsko kodo piše več ljudi. Znebimo se najprej šestice. To storimo tako, da na obeh straneh enačbe prištejemo 6, saj je 6 na levi negativna (levo od nje stoji minus). 6 na levi tako nimamo več, na desni pa smo petici prišteli 6 in dobili 11. "Zelenega" člena na levi ni več, tako v računu, kot v verigi. Sedaj se znebimo še dvojke na levi, s tem, da na obeh straneh enačbe odštejemo 2, saj je 2 pozitivna (levo od nje stoji plus). Sedaj tudi 2 na levi nimamo več. Na desni pa smo 1 odšteli 2 in dobili 9. "Modrega" člena na levi ni več, tako v računu, kot v verigi, ostal je le še "rdeči" člen, ta, ki vsebuje iskano spremenljivko (x): Če iskano spremenljivko želimo "osvoboditi", moramo uporabiti kladivo :) V resnici ne bomo uporabili kladiva, želimo samo poudariti, da ima računska operacija deljenja, ki jo bomo sedaj izvedli na obeh straneh enačbe, večjo "moč" od seštevanja in odštevanja, ki smo ju izvedli v prejšnjih dveh korakih. Enako "moč" kot deljenje ima tudi množenje. In še nekaj zelo pomembnega: Orodje z največjo močjo uporabimo vedno na koncu. Tako kot v računalniških igricah ali pri kosilu - najboljše pustimo za konec :) Obe strani enačbe delimo s 3 in dobimo rezultat: To seveda ni univerzalen način reševanja enačb, si pa lahko z njim pomagamo pri "prvih korakih".
Mogoče kdo vpraša: "Kaj pa, če je neznanka v več členih?" V tem primeru pa take člene lahko združimo: 2x + 3x + 5 = 20 5x + 5 = 20 Seveda bi tudi našo enačbo lahko rešili hitreje; če nam negativna števila ne povzročajo težav, lahko zapišemo: 3x + 2 - 6 = 5 3x - 4 = 5 |
ARHIV
May 2024
KATEGORIJE
All
|
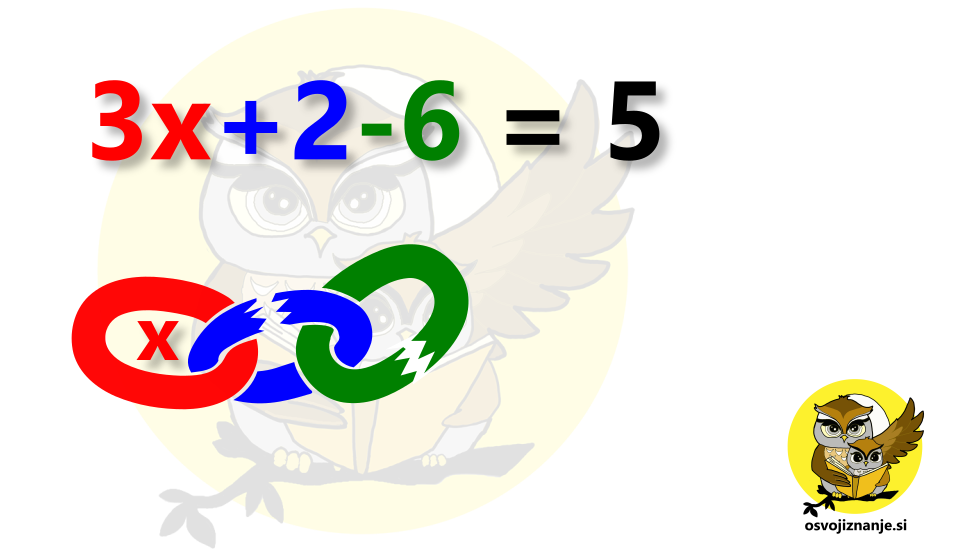
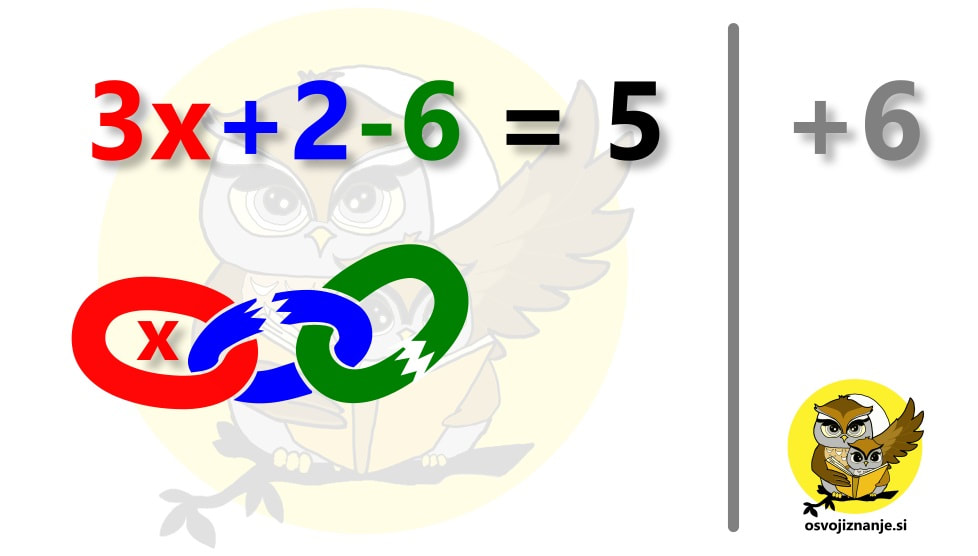

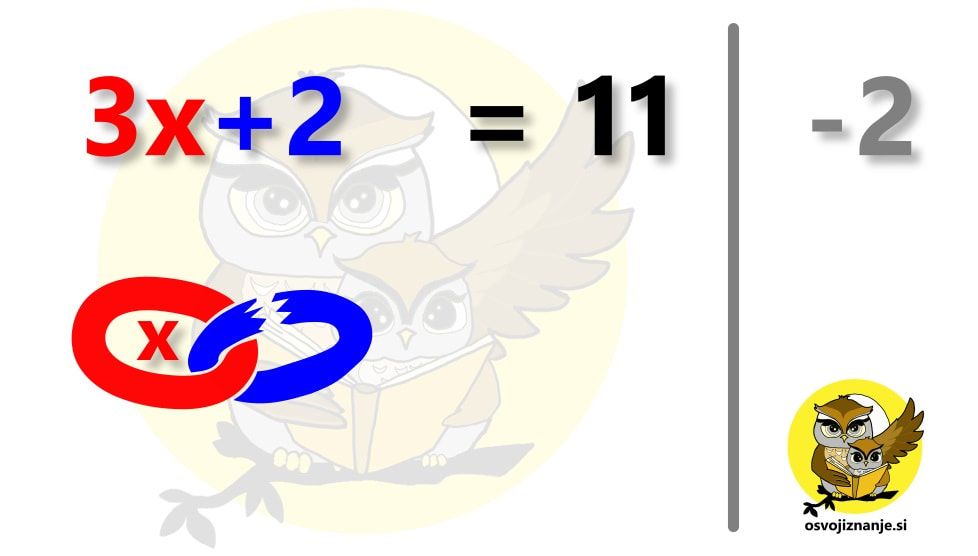


 RSS Feed
RSS Feed
