|
Verjetno se nihče ne bi branil "nevidne sile", ki bi ga rešila vsakič, ko bi zašel v težave. Verjeli ali ne, v matematiki taka "sila" dejansko obstaja. To je število 1, ki ga v redovalnici seveda ne maramo, :) v matematičnem zvezku pa pride še kako prav.
Število 1 imenujemo tudi enota (oziroma nevtralni element) za množenje, to pa zato, ker je rezultat množenja katerega koli števila z 1 kar število samo (če koga zanima več o tem, lahko pokuka sem). Zakaj "nevidna"? Oglejmo si izraz ab. Ta izraz lahko pomnožimo z 1 tolikokrat, kot želimo, pa bo še vedno enak 1: ab⋅1 = ab⋅1⋅1 = ab⋅1⋅1⋅1 = ... = ab Ker vemo, da množenje nekega člena (če se sprašujete, kaj je to člen, lahko na hitro pokukate sem) z 1 samega člena ne spremeni, enice nima smisla pisati, dobro pa je vedeti, da je tam. :) Kateremu faktorju pripada minus? Člen -ab sestavljata dva faktorja, predznak pa nam sporoča, da je ta člen negativen. Kateremu faktorju pripada minus? Načeloma lahko pripada a-ju ali pa b-ju (saj poznate tisto: plus in minus pri množenju vrne minus ...), da se ne bomo kregali, pa lahko rečemo tudi nobenemu. :) Kako? Pomnožimo vse skupaj še z 1 in dobimo. -1ab oziroma (-1)ab. Tu pa se lepo vidi, da je minus "ukradla" enica. Ti, ti, enica :) Kako pri razstavljanju izrazov "ukalupiti" enačbo? Enačba za razliko kvadratov se glasi: a²-b² = (a+b)(a-b) Kaj pa, če imamo v izrazu recimo a²-1? Desni člen lahko mirno pomnožimo z 1 in dobimo: a²-1² To pa je že lažje, kajne? :) Podobno lahko storimo tudi z izrazom -a²+b². V enačbi je prvi člen pozitiven, drugi pa negativen, mi pa imamo ravno nasprotno situacijo. Tokrat z 1 pomnožimo kar oba člena: -1a²+1b², nato pa izpostavimo (-1): -1(a²-b²) in v oklepaju dobimo to, kar želimo. :)
0 Comments
Poleg splošnega produkta različnih dvočlenikov ... (a+b)(c+d) ... sta pogosto v uporabi tudi posebna primera:
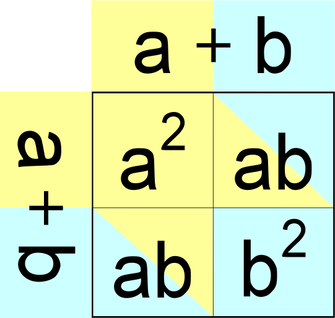
Enačbi za posebna primera je koristno poznati, saj ju potrebujemo pri razstavljanju. Za lažje pomnjenje si vse tri poglejmo v grafični obliki. Splošen produkt različnih dvočlenikov Enačba za splošen produkt različnih dvočlenikov se glasi: (a+b)(c+d) = ac+bc+ad+bd V grafični obliki enačba izgleda takole: Kvadrat dvočlenika Enačba za kvadrat dvočlenika se glasi: (a+b)² = a²+ab+ab+b² = a²+2ab+b² V grafični obliki enačba izgleda takole: Če je člen a ali b negativen, se predznak kvadratov (a² oziroma b²) ne spremeni, predznak srednjega člena (2ab) pa določimo po oranžnem pravilu množenja in deljenja:
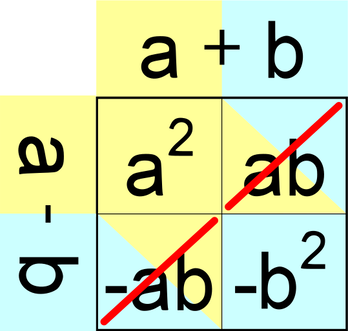
Produkt vsote in razlike enakih števil Enačba za produkt vsote in razlike enakih števil se glasi: (a+b)(a-b) = a²+ab-ab-b² = a²-b² V grafični obliki enačba izgleda takole: Na sliki se lepo vidi, da se srednja dva člena v računu okrajšata.
Ni panike, uporabi Vietovo pravilo, pri čemer upoštevaš, da je linearni koeficient enak nič:
x²-9 je isto kot x²+0x+9. Ker je linearni koeficient enak 0, je potrebno prosti člen (9 v zgornjem izrazu) predstaviti kot zmnožek dveh nasprotno enakih števil (+√9 in - √9 oz. +3 in -3 v zgornjem izrazu). Velja torej: x²-9 = (x+3)(x-3). V nadaljevanju sledi razlaga za razstavljanje izrazov po Vietovem pravilu. Postopek je uporaben za "lažjo obliko" izraza, pri čemer predpostavimo:
Razložimo zgornji izraz:
Sedaj pa navodilo. Aha, preden se lotimo reševanja, povejmo še, kaj pričakujemo za rešitev :) Ker je spremenljivka v zgornjem izrazu x, bo rešitev v obliki (x±a)(x±b). X je seveda spremenljivka, a in b pa bomo določili z naslednjim postopkom:
|
ARHIV
May 2024
KATEGORIJE
All
|
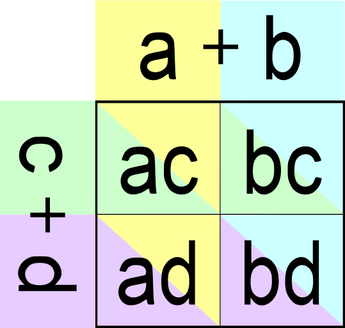
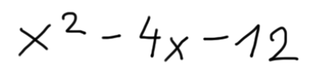
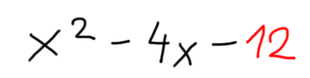
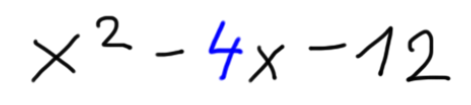
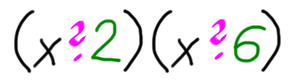
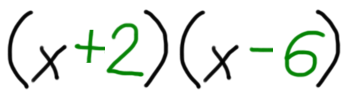
 RSS Feed
RSS Feed
