|
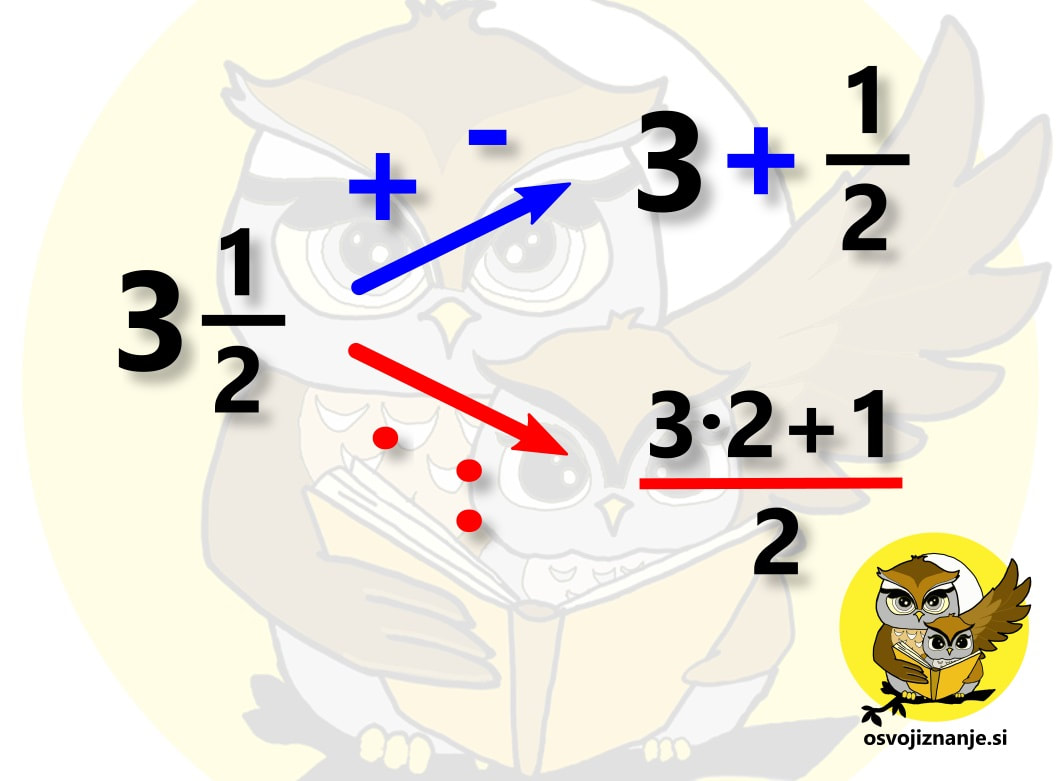
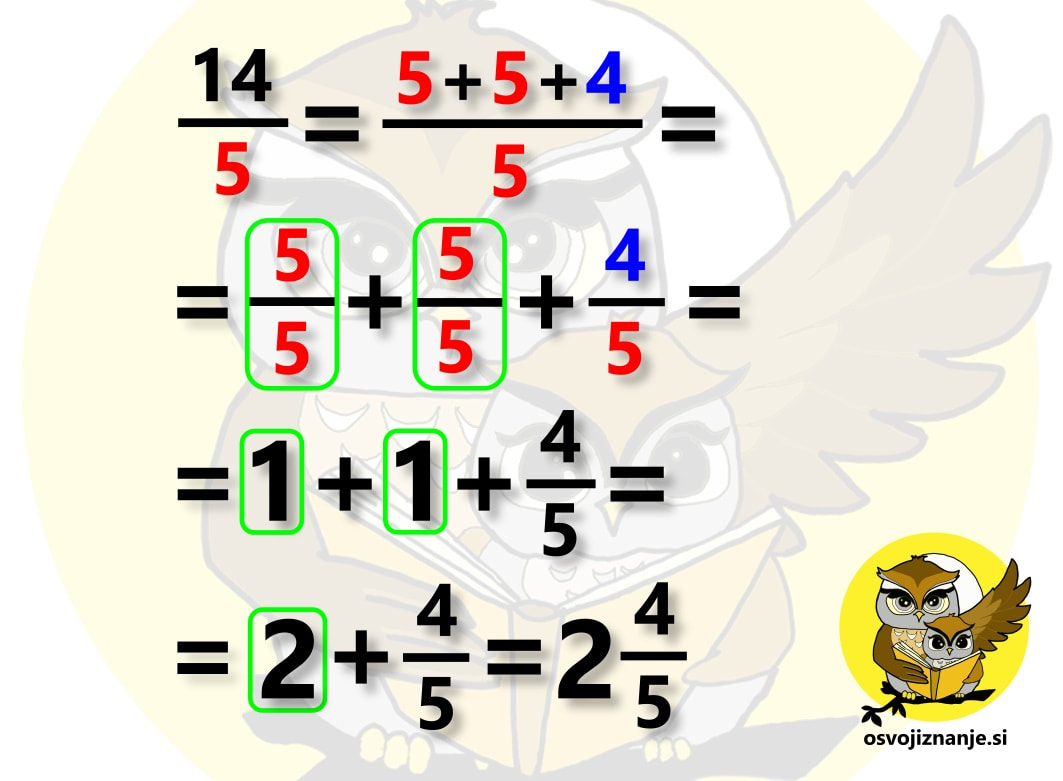
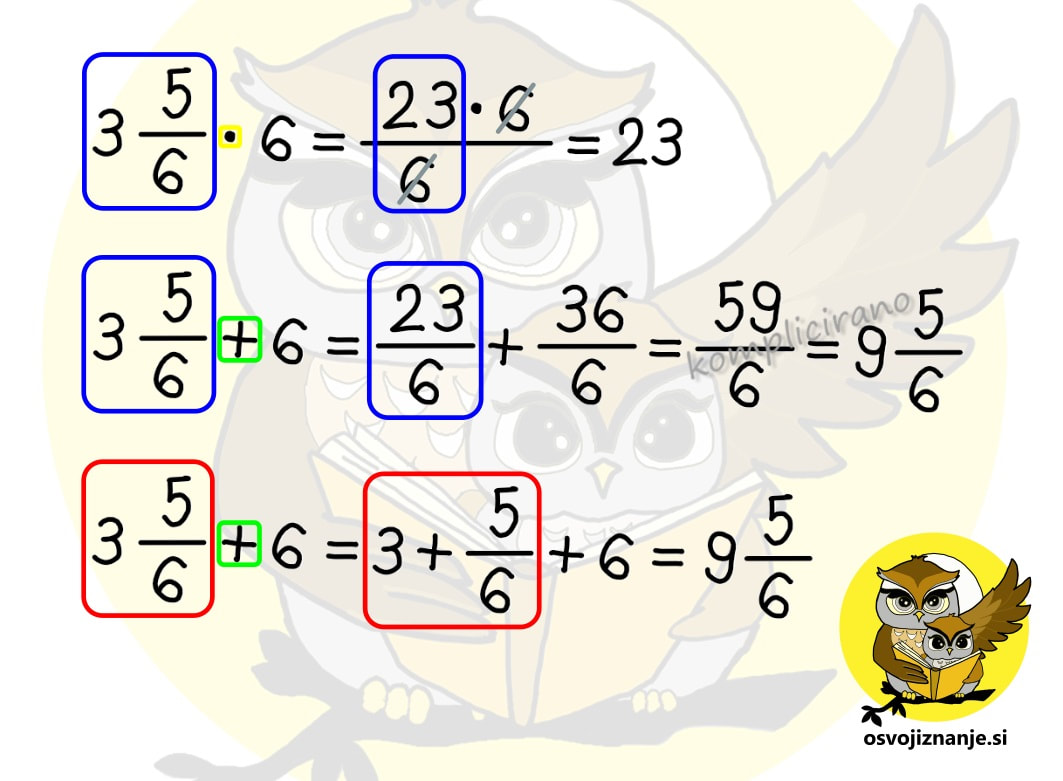
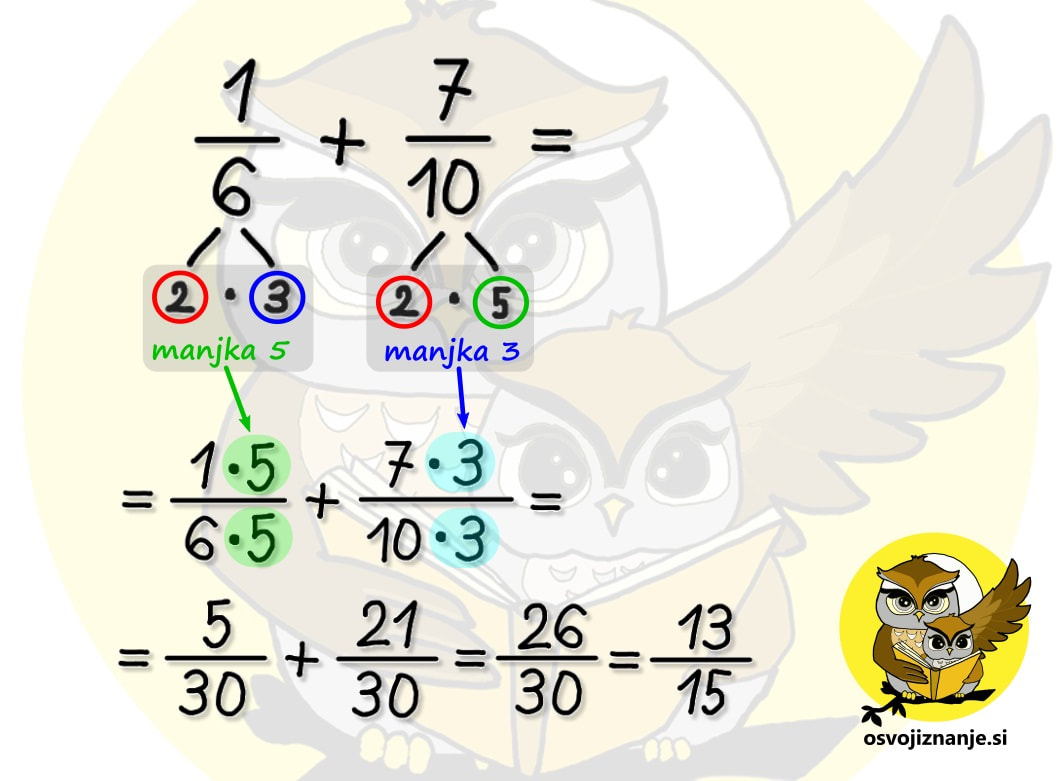
Sedmi razred je pri matematiki za marsikoga kar zalogaj. Praštevila, nato pa ulomki in vse kar pride zraven – krajšanje, razširjanje, primerjanje, iskanje skupnega imenovalca ... in seveda računanje z ulomki. Najprej osnovne računske operacije (seštevanje, odštevanje, množenje in deljenje), nato pa kombinacije le-teh. Da je zadeva še bolj zanimiva, se ulomkom pridružijo še cela, mešana in decimalna števila. Pri obravnavi snovi se seveda vedno mudi in kdor je v nižjih razredih »prešprical« kakšno snov ali pa jo zgolj pozabil (vsi smo ljudje), se hitro znajde v težavah. Da v takih primerih ne bi bilo potrebno takoj klicati inštruktorja, sem pripravil nekaj hitrih nasvetov za »spopad z ulomki«. :) Kako obravnavati mešano število? Mešano število je število, ki je sestavljeno iz celega števila in ulomka, na primer 3 in ena polovica (glej sliko). Marsikdo ob pogledu na tako število začne v imenovalcu takoj množiti 3 z 2 in prištevati 1 ... (spodnji ulomek na desni strani slike). To je seveda pravilen postopek, a ga ni »modro« uporabljati v vseh primerih, ampak le pri množenju in deljenju. Pri seštevanju in odštevanju pa je mešani ulomek lažje zapisati »na dolgo« in sicer v obliki celo število + ulomek (zgornji ulomek na desni strani slike). Zakaj »na dolgo«? Zato, ker je zapis mešanega števila v bistvu skrajšan zapis vsote celega števila in ulomka. Kako odšteti ulomek od celega števila? V takem primeru lahko uporabimo t.i. »strategijo izposojanja«. V našem primeru na spodnji sliki si od 3 »izposodimo« 1, ki jo nato zapišemo v obliki ulomka. Število 1 v obliki ulomka zapišemo tako, da izenačimo vrednost števca in imenovalca, ta pa je lahko karšna koli celoštevilska vrednost. Ker v našem računu nastopa še en ulomek, ki ima vrednost imenovalca 7, enako vrednost uporabimo tudi pri ulomku, ki predstavlja celoto, saj nam tako ni potrebno iskati skupnega imenovalca. Enako strategijo lahko uporabimo tudi pri odštevanju ulomka od mešanega števila, če je ulomek, ki ga odštevamo, večji od ulomka zraven celega števila (npr. 5 2/5 – 3/5). Kako odšteti mešani ulomek? Za mešani ulomek vemo, da je skrajšan zapis vsote celega števila in ulomka. Če tak ulomek prištevamo, lahko enostavno zapišemo celo število + ulomek. Če pa ga odštevamo, ne smemo pozabiti, da minus pred njim »zagrabi« tako na celo število kot na ulomek (podobno kot če bi imeli oklepaj), zato je potrebno odšteti tako celo število kot ulomek. Kdaj je priporočljivo »nepravi ulomek« spremeniti v mešano število in kako to storim? Če ima ulomek »zgoraj več kot spodaj« oziroma ima števec večji od imenovalca, zanj rečemo, da je nepravi. Tak ulomek je »vreden« več kot 1, zato »lepše«, če ga zapišemo kot vsoto celega števila in ulomka oziroma »tistega, kar ostane«. Vemo, da ulomke seštevamo tako, da števce seštejemo, imenovalec pa prepišemo. Kaj pa, če bi to pravilo uporabili »v rikverc«? Števec ulomka lahko zapišemo kot vsoto vrednosti v imenovalcu in ji prištejemo »tisto, kar ostane«. V našem primeru števec 14 zapišemo kot vsoto dveh petic in »preostale« štirice (5+5+4). Tak ulomek lahko razdelimo na 3 ulomke (5/5, 5/5 in 4/5), od katerih sta prva dva enaka 1, zato ju lahko zapišemo kot celoštevilsko vrednost 2, zadnji ulomek (4/5) pa dopišemo zraven. Kdaj moram mešano število spremeniti v »nepravi ulomek« in kako to storim? Takrat, kadar mešano število množimo ali delimo s celimi števili ali ulomki. Primer množenja mešanega števila s celim številom je prikazan v prvi vrstici spodnje slike. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Druga in tretja vrstica spodnje slike predstavljata isti račun (seštevanje mešanega števila s celim številom), rešen na dva načina. V drugi vrstici vidimo, da smo iz povsem enostavnega seštevanja znotraj desetice prišli na račun 23+36, katerega rezultat je potrebno potem deliti še s 6, da dobimo celi in ulomljeni del rešitve. V tretji vrstici pa enostavno seštejemo celi števili, prištejemo ulomljeni del in brez pretiranega napora dobimo, seveda, enak rezultat. :) Kako najlažje poiščem (najmanjši) skupni imenovalec? Pred časom sem na inštrukcijah poskusil z metodo »nogic« oziroma »rožičkov«, ki se jo mogoče kdo spomni še iz nižjih razredov osnovne šole. Za razliko vrednosti na krajiščih »nogic« tu ne seštevamo ampak množimo, pred tem pa število razcepimo na prafaktorje. Ker to počnemo grafično, zadeva utegne postati celo zabavna. ;) Več o sami metodi si lahko preberete v članku o računanju s pomočjo številskih dreves. V čem je »trik«? Vzemimo za primer račun s spodnje slike. Prvi seštevanec ima imenovalec enak 6, drugi pa 10. Po razcepu na praštevila na »nogice« prvega imenovalca zapišemo 2 in 3 (2 · 3 = 6), na nogice drugega pa 2 in 5 (2 · 5 = 10). »Fora« najmanjšega skupnega imenovalca je v tem, da s »čim manj potezami« imenovalca izenačimo. Pri tem seveda lahko uporabimo zgolj računsko operacijo množenja, množiti (z istim številom!) pa moramo tako »spodaj« (imenovalec) kot »zgoraj« (števec), sicer vrednost ulomka spremenimo, kar pa ni okej. Poglejmo, kako lahko imenovalca izenačimo v našem primeru. Prvi ulomek »ima« 2 in 3, drugi pa 2 in 5. Z »najmanj potezami« imenovalca izenačimo tako, da na prvi imenovalec dodamo (števec in imenovalec množimo s) 5, na drugega pa 3. Tako sta oba imenovalca enaka 2 · 3 · 5 = 30, števca pa sta po množenju enaka 5 oziroma 21. Ulomka nato še seštejemo in okrajšamo oziroma poenostavimo in dobimo rezultat trinajst petnajstin. Če imamo večja števila, imenovalce lako »drobimo« postopoma (drevo se bolj razveji), upoštevamo pa zgolj številke na končnih vej(ic)ah. Te za boljšo vidnost lahko tudi obkrožimo. Ko smo že nekoliko bolj izkušeni, nam imenovalcev ni potrebno drobiti povsem do praštevil. Če imamo na primer imenovalca enaka 8 in 12, lahko zapišemo 8 kot 2 · 4, 12 pa kot 3 · 4. 4 nam ni potrebno drobiti naprej na 2 · 2, saj se 4 nahaja v obeh imenovalcih s takim »kompliciranjem« ne bi nič pridobili, le hitreje bi se lahko zmotili. :) To je seveda zgolj eden izmed možnih načinov. Če v njem nekako »ne najdete«, pa lahko »pokukate« še tale članek. Kdaj moram »obrniti ulomek«? Računanju z obračanjem ulomka »uradno« rečemo množenje z obratno vrednostjo ulomka. Ker je deljenje z ulomkom »smotano« :) (pojavijo se dvojni ulomki in druge neprijetnosti), raje uberemo drugo pot, pri čemer modro izkoristimo naslednja dejstva:
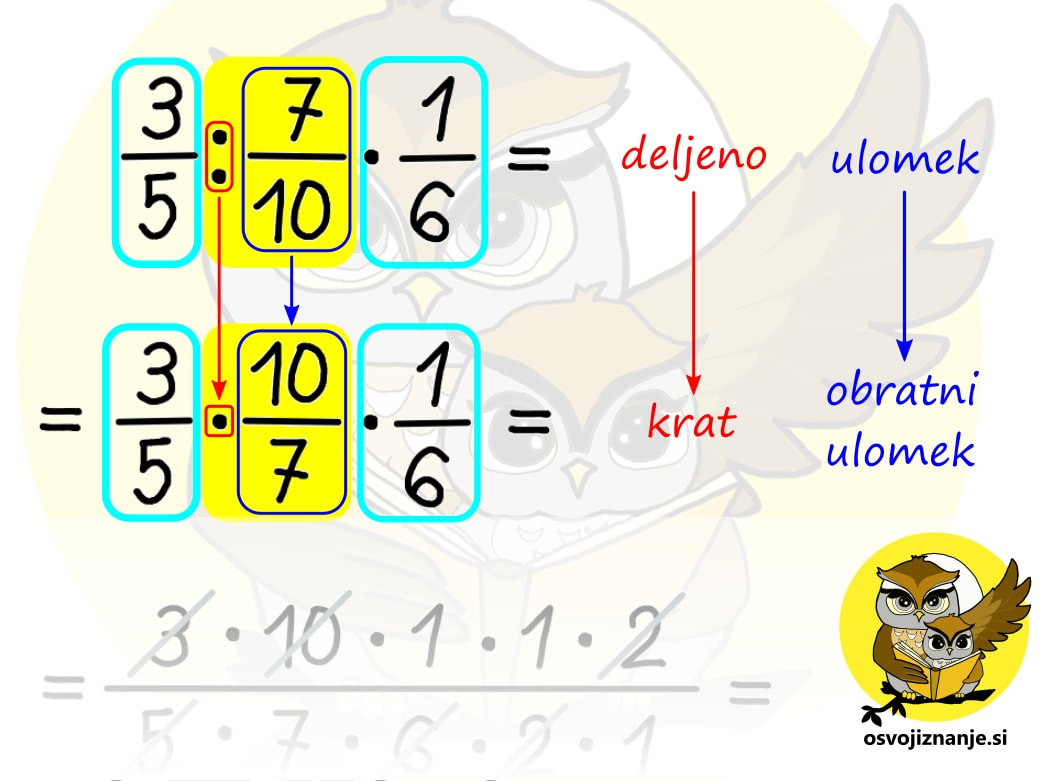
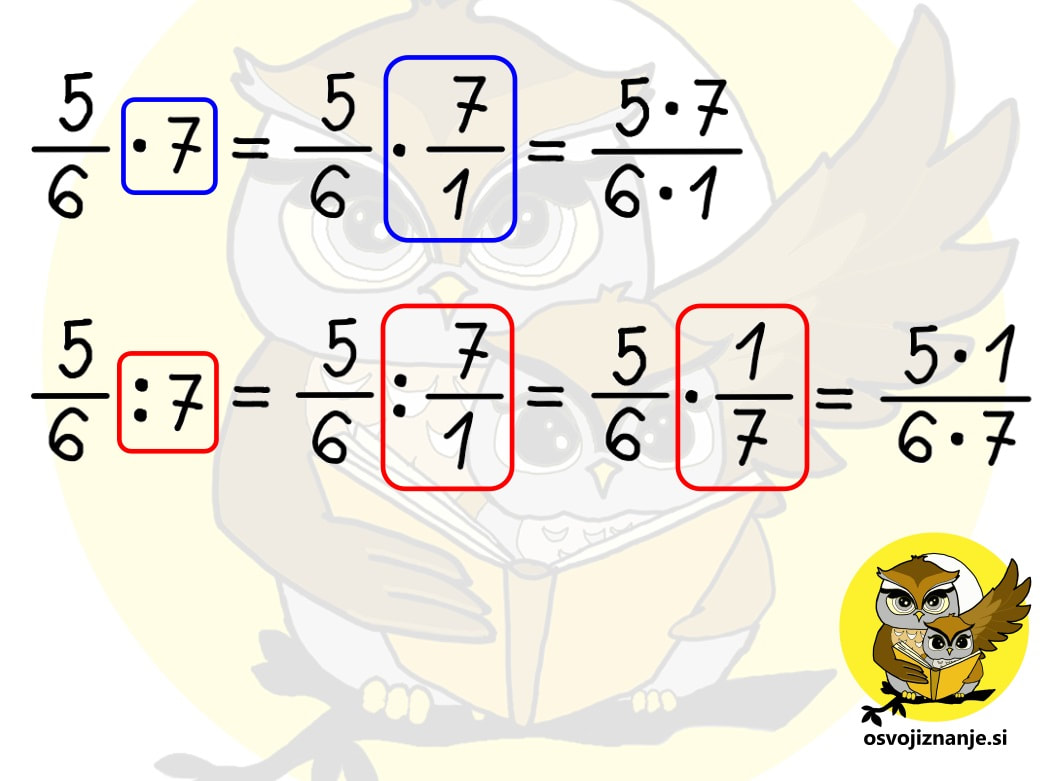
Iz tega sledi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Obratno vrednost ulomka določimo zelo enostavno, saj zgolj zamenjamo vrednosti števca in imenovalca (ulomek obrnemo »na glavo«). :) Kdaj moramo torej »obrniti ulomek«? Vsakič, kadar računsko operacijo deljenja zamenjamo z množenjem. In zakaj to počnemo? Zato, ker je množenje z ulomkom enostavnejše od deljenja. A ne pozabimo: obrnemo vedno zgolj tisti ulomek, ki stoji desno od znaka za deljenje (ki postane znak za množenje)! Še nekaj za »nerde«. Če potegnemo analogijo s seštevanjem in odštevanjem, lahko zapišemo ...
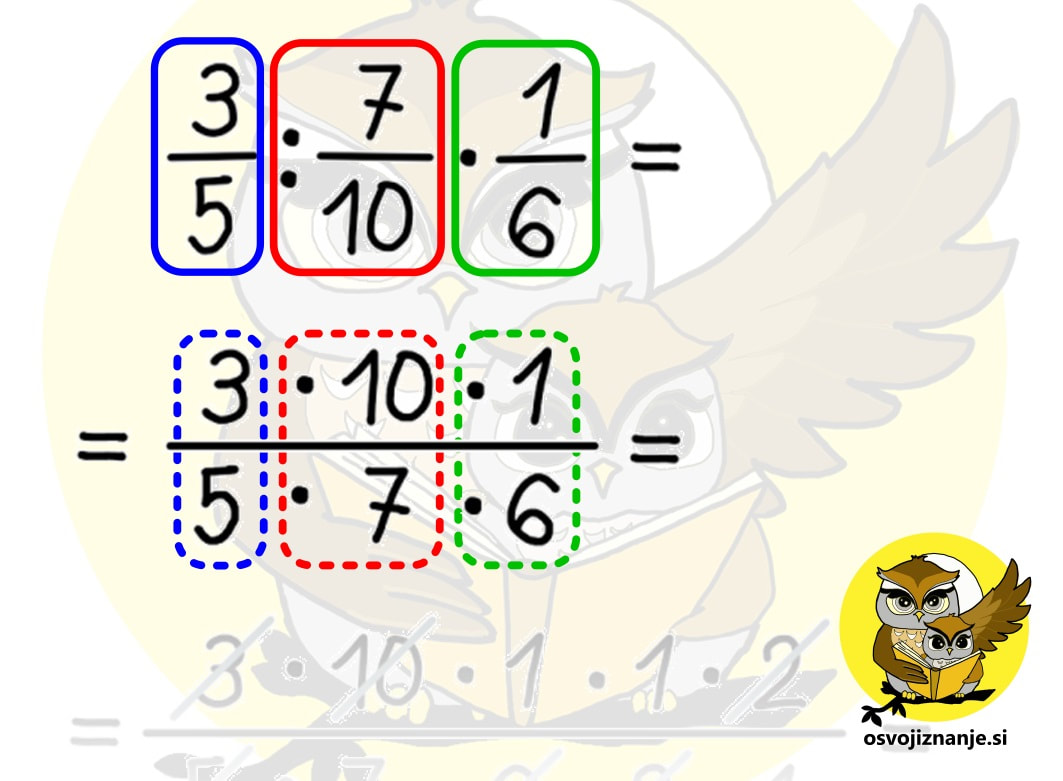
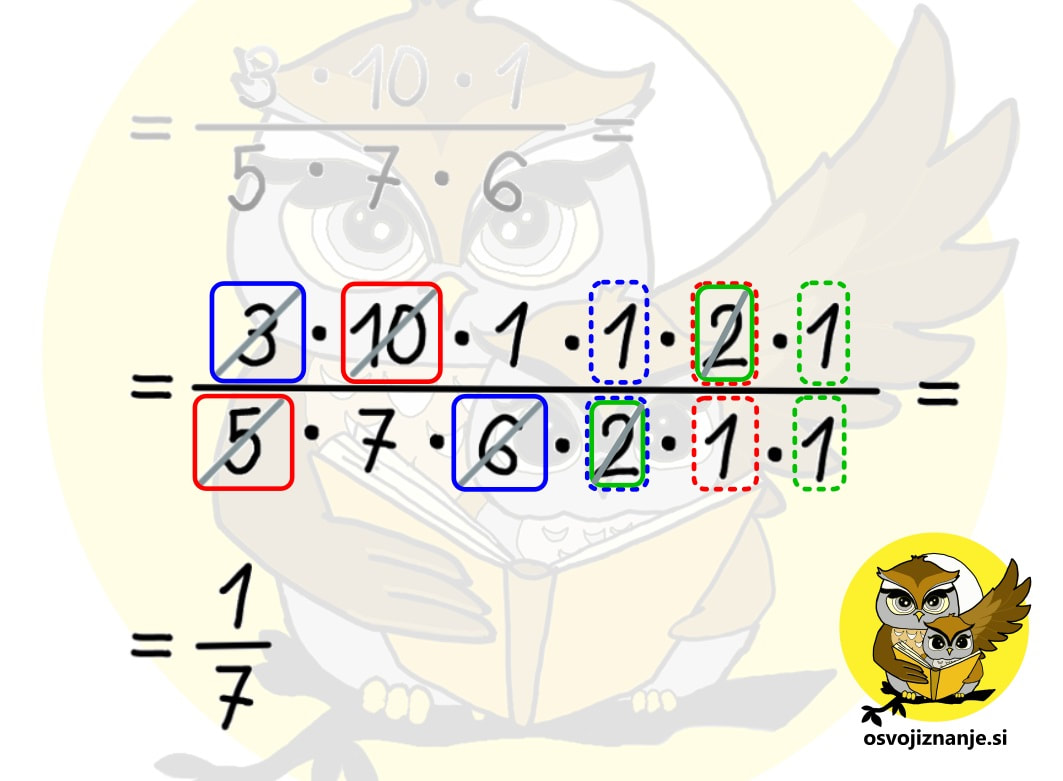
Za konec pa še nekaj za »toplt nerde« :) Vemo, da velja enakost a-(-a) = a+a. Po analogiji bi lahko zapisali tudi a:(:a) = a·a, ampak bi nas kak matematik »za ušesa«. :) Omenjeni zapis namreč ni dovoljen, saj »:« v prvem oklepaju ni predznak, tako kot »-« v drugem oklepaju. Lahko pa drugi zapis popravimo v a:(1:a) = a·a oziroma v a:(1/a) = a·a. Pa smo spet pri naši ugotovitvi, da je deljenje z nekim številom enako množenju z njegovo obratno vrednostjo. Pa še nekaj. Predznaka »+« nikoli ne pišemo, čeprav »vemo, da je tam«. Zato tudi prvi člen na skrajni levi strani računa v primeru, da je pozitiven, nima predznaka. Po drugi strani moramo predznak »-« vedno zapisati. Kadar imamo opravka hkrati s predznakom »+« ali »-« in računsko operacijo »+« ali »-«, velja pravilo, da dva »-« dasta »+« (o, ko bi bilo tako tudi pri ocenjevanju!) :) Predznaka »krat« in »deljeno« pa kot taka ne obstajata, zato se nikoli ne bomo srečali npr. z računom 10:(:5), bomo pa srečali račun npr. 10:(1/5), ki se od prvega praktično ne razlikuje, saj enica pri množenju in deljenju ne spremeni vrednosti računa. In tu se lahko spomnimo pravila »dva minusa dasta plus«, saj analogno tudi »dve deljenji dasta množenje« (matematiki bi nas spet za ušesa :)) in račun 10:(:5) oziroma 10:(1/5) postane 10 · 5. To si velja zapomniti, saj nas analogija pogosto lahko reši iz zadrege, če kaj pozabimo. A pozor – učitelju ne skušajte »prodati« računa 10:(:5), ampak vmes vrinite tisto enico (10:(1/5)), da vas – ne bo za ušesa seveda. :) Več na temo povezav med seštevanjem in odštevanjem oz. med množenjem in deljenjem ter nasprotnih in obratnih vrednostih pa najdete v samostojnem članku. Kdaj lahko »dam vse na eno dolgo ulomkovo črto«? Kadar imamo v računu (ali v delu računa) samo množenje in deljenje ulomkov ter celih števil, lahko vse skupaj zapišemo na eno ulomkovo črto, ki jo po potrebi podaljšamo (če je možno kaj »krajšati« oziroma, bolj pravilno rečeno, poenostaviti). Pri zapisu na »dolgo« ulomkovo črto ulomkov, pred katerimi stoji znak za deljenje, ne pozabimo »obrniti okoli«. Deljenje se v tem primeru spremeni v množenje, tako da ima taka »dolga« ulomkova črta tako v števcu kot v imenovalcu zgolj računsko operacijo množenja, kar nam omogoča enostavno krajšanje. Ali lahko ulomke lahko krajšam »križkraž«? Seveda. In to večkrat. :) Zakaj? Ker imamo tako v imenovalcu kot v števcu račun, ki vsebuje zgolj množenje, za katerega velja zakon o zamenjavi (recimo 3 krat 5 je isto kot 5 krat tri ...) Na spodnji sliki vidimo, da 3 v števcu in 6 v imenovalcu lahko krajšamo s 3, 10 v števcu in 5 v imenovalcu pa z 2, kljub temu, da ne ležijo »eden pod drugim«. 2 v imenovalcu iz prvega krajšanja in 2 v števcu iz drugega krajšanja lahko nato še enkrat krajšamo z 2. Aja, pa še nekaj. Lepše kot »krajšati« se sliši »poenostaviti«, saj po tem postopku ulomek ni nič »krajši«, J ampak zgolj poenostavljen, saj je vrednost okrajšanega ulomka enaka »originalnemu« ulomku. Kdaj je priporočljivo celo število pretvoriti v ulomek in kako to storim? Kadar celo število nastopa "v družbi ulomkov" v računu množenja ali deljenja, ga je najbolj enostavno pretvoriti v ulomek in nato z njim računati tako kot z ulomkom. Na ta način se ne bomo nikoli spraševali, ali ga je potrebno zapisati v števec ali imenovalec ulomka. Celo število v ulomek pretvorimo tako, da ga zapišemo v števec (zgoraj), v imenovalec (spodaj) pa zapišemo vrednost 1. Dokaj logično, če vemo, da ulomek predstavlja deljenje, deljenje z 1 pa na deljenca nima vpliva. Primer: 5=5/1. Če s tem številom množimo, vemo, da gre 5 v števec "dolge ulomkove črte", 1 pa v imenovalec. Če pa z njim delimo, vemo, da ga moramo "obrniti na glavo", zato na "dolgo ulomkovo črto" zapišemo 1 zgoraj, 5 pa spodaj. Če imamo poleg celega števila zraven še ulomek, je tak zapis pri množenju in deljenju potrebno pretvoriti v »nepravi ulomek«. Za več »poskrolajte« malo višje po članku. Pri seštevanju in odštevanju pa cela števila in ulomke lahko seštevamo oz. odštevamo ločeno in jih na koncu združimo, tako da pretvorba celih števil v ulomke ni potrebna, še več, s tem si lahko enostavno nalogo celo zakompliciramo. Če »gremo kje čez«, nepravi ulomek pretvorimo v pravega, celoštevilski del pa ustrezno povečamo. Če »nam kje zmanjka«, pa si od celega števila »izposodimo« ulomek tipa n/n in odštevanje izvedemo posebej za cela števila in posebej ulomke. Za podrobnejšo razlago »poskrolajte« malo višje po članku. Kdaj je koristno decimalno število pretvoriti v ulomek?
Marsikdo »ne mara ulomkov«, zato v računih, kjer nastopa kombinacija decimalnih števil in ulomkov, slednje vedno pretvori v decimalna števila in se potem »igra s premetavanjem decimalnih vejic«. Poleg tega, da je tako računanje »manj elegantno«, rezultat take pretvorbe ni vedno končno decimalno število, zato ga moramo zaokrožiti, s čimer pa »pridelamo« tudi nekaj pogreška. Zakaj je računanje s pretvorbo ulomkov v decimalna števila »manj elegantno«? Naloge so velikokrat zastavljene tako, da je pri računanju z ulomki »manj pisanja« in veliko faktorjev se »lepo krajša«, tako da tak račun izgleda »lepše« oziroma bolj pregledno. Po drugi strani se pri računanju z decimalnimi števili ni potrebno ukvarjati s pravili za računanje z ulomki, a moramo biti zelo pozorni na decimalne vejice. V računih, kjer nastopa kombinacija decimalnih števil in ulomkov, je decimalno število koristno pretvoriti v ulomek predvsem pri množenju in deljenju z ulomki, medtem ko je pri seštevanju in odštevanju včasih lažje, če naredimo obratno – ulomek pretvorimo v decimalno število, predvsem takrat, kadar je rezultat take pretvorbe končno decimalno število.
0 Comments
Glede na to, da je ena izmed interpretacij ulomkov razmerje, bi ulomke lahko krajšali in razširjali oziroma pretvarjali na določeni števec ali imenovalec tudi s tabelo razmerij (angl. ratio table). Preden si ogledamo nekaj primerov, najprej razmislek v povezavi z izrazoma krajšanje in razširjanje ulomkov. Pam Harris, predavateljica na Teksaški univerzi, avtorica številnih knjig in promotorka poučevanja t.i. »prave matematike« (angl. »real math«) me je opozorila, da je primernejši izraz za hkratno deljenje števca in imenovalca z istim številom poenostavljanje, saj vrednost ulomka po »krajšanju« ni nič manjša kot prej. Tudi »razširjanje ulomka« bi bilo po tej analogiji bolje imenovati pretvorba ulomka na določeno vrednost števca oz. imenovalca. Primer 1: poenostavi ulomek 180/300:
Števec in imenovalec smo dvakrat razpolovili (deljenje ulomka z 2), nato pa ju delili s 3 in nazadnje s 5. Primer 2: pretvori ulomek na vrednost števca 18:
Števec in imenovalec smo trikrat podvojili (množenje ulomka z 2), nato pa sešteli vrednosti v prvem in četrtem stolpcu s številkami (2+16=18, 3+24=27). Pozor! Tu ne gre za seštevanje ulomkov 2/3 in 16/24! Pomislimo na reševanje sistemov enačb (metoda nasprotnih koeficientov) ... Pri takem sklepanju se osredotočimo na števec, a ne pozabimo na imenovalec! Primer 3: pretvori ulomek na vrednost imenovalca 100:
Števec in imenovalec smo podvojili, nato pa smo ju pomnožili še z 10.
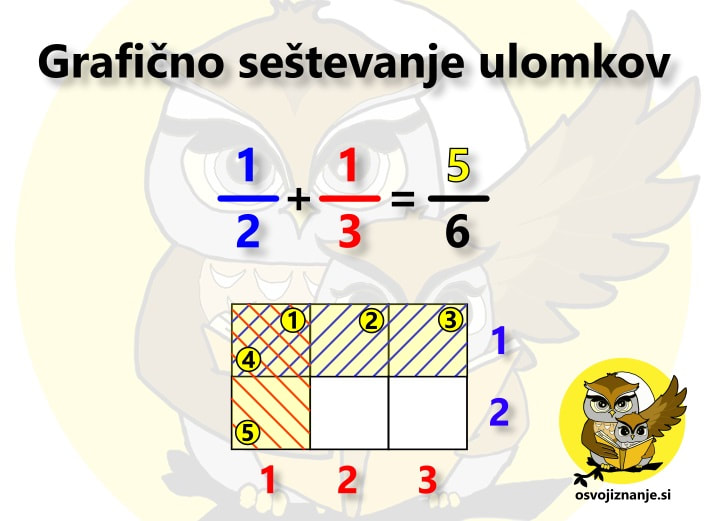
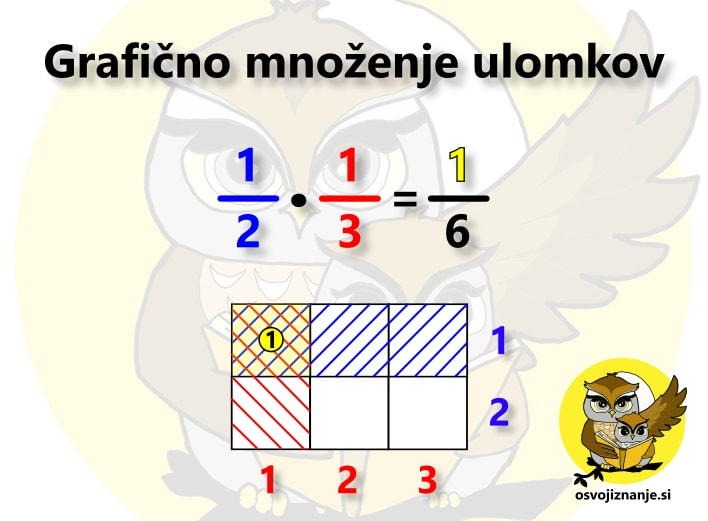
Pri takem sklepanju se osredotočimo na imenovalec, a ne pozabimo na števec! Za konec pa še odgovor na vprašanje: »Zakaj je pretvarjanje ulomkov sploh potrebno?« V tem najdemo vsaj dva smisla. Zakaj poenostavljamo, nam pove že samo ime – zato, da je ulomek enostavneje zapisati, ga prebrati, si ga zapomniti ... Pretvarjanje na določeno vrednost imenovalca, točneje na potence števila 10, pa nam pomaga pri pretvorbi ulomka v decimalno število ali odstotek. Smisla pretvarjanja na določeno vrednost števca pa do danes še nisem našel, čeprav v učbenikih najdemo tudi take naloge. :) ... oziroma uporaba logike pri uri aritmetike. Pri seštevanju ulomkov »na klasičen način« vemo, da jih moramo najprej »spraviti na skupni imenovalec«, nato pa sešteti števce le-teh. Na koncu ulomek, ki predstavlja vsoto, še okrajšamo. Kako pa bi to storili grafično? Oglejmo si račun 1/2+1/3. Ker ulomek predstavlja del celote, eno polovico lahko predstavimo tako, da celoto razdelimo na dva enaka dela in enega pobarvamo. Z eno tretjino storimo podobno, le da celoto razdelimo na tri enake dele. Kako pa bi naenkrat lahko predstavili oba ulomka? Z dvodimenzionalnim poljem oziroma tabelo. S stolpci prikažemo en ulomek, z vrsticami pa drugega. V našem primeru torej potrebujemo tabelo z dvema stolpcema in tremi vrsticami (lahko storimo tudi obratno, saj za vsoto velja zakon o zamenjavi). Modra šrafura na sliki predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3. Sedaj pa »vklopimo logiko«. V Booleovi algebri simbol »+« pomeni disjunkcijo oziroma logični »ali«. V izjavni logiki (angl. propositional logic) to povezavo označimo z znakom »∨«, v teoriji množic pa z znakom »∪«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »∥« ali zgolj angleškem izrazu »OR«. Kaj to pomeni za našo tabelo s prikazom ulomkov? S pomočjo uporabe logike lahko iz nje neposredno zapišemo rezultat našega računa. Ker ima tabela 6 polj, je imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Kaj pa števec? Ker imamo logično relacijo »ali«, moramo prešteti vsa polja, ki so šrafirana ali modro ali rdeče. Eno polje je šrafirano z dvema barvama, torej ga moramo šteti dvakrat. Imamo torej eno modro, dve rdeči in eno dvobarvno šrafirano polje, skupaj torej 1+2+2 oziroma 5 polj. Števec je torej 5, kar pomeni, da je vsota enaka 5/6. Pri množenju ulomkov »na klasičen način« pa zmnožimo tako števce kot imenovalce ter okrajšamo, »kar se da«. Za primer uporabimo ista ulomka, le da ju tokrat zmnožimo. Iščemo torej produkt 1/2 · 1/3. Ulomka predstavimo na povsem enak način kot pri seštevanju, le rezultat bomo prebrali drugače. Zopet imamo torej tabelo z 2 stolpcema in 3 vrsticami, kjer modra šrafura predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3. Ponovno »vklopimo logiko«. V Booleovi algebri simbol »*« pomeni konjunkcijo oziroma logični »in (hkrati)«. V izjavni logiki to povezavo označimo z znakom »∧«, v teoriji množic pa z znakom »∩«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »&« ali zgolj angleškem izrazu »AND«. S pomočjo naše tabele zapišimo še rezulat. Ker ima tabela 6 polj, je tudi tu imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Pri števcu pa bo nekoliko drugače. Ker imamo logično relacijo »in hkrati«, moramo prešteti vsa polja, ki so šrafirana tako modro kot rdeče. Tako je le eno polje, kar pomeni, da je števec enak 1. Zmnožek ulomkov 1/2 in 1/3 je torej enak 1/6. Omenjena metoda je mogoče nekoliko daljša od »klasične«, saj je tu in tam potrebno kakšen rezultat še dodatno okrajšati, nam pa omogoča zelo dober vpogled v koncept računanja z ulomki, česar nam »piflarski« postopki ne nudijo.
Ste pogrešili odštevanje in deljenje? Odštevanje je »pokrito« s prištevanjem nasprotne vrednosti, deljenje pa z množenjem z obratno vrednostjo. Na koncu pa še vprašanje za vas. Kako bi grafično predstavili vsoto oziroma zmnožek treh ulomkov? Ulomkov marsikdo ne mara, delno tudi zato, ker jih v izrazih ne moremo preprosto seštevati in odštevati, ampak jih moramo prej vedno razširiti na najmanjši skupni imenovalec: Nekoliko raje jih imamo v enačbah. Tu nam ulomkov ni potrebno razširjati na najmanjši skupni imenovalec, ampak z njim preprosto pomnožimo obe strani enačbe. Najboljše pri vsem tem je pa to, da gredo na ta način ulomki pa pa 😉
Kako si zapomniti, katera številka v ulomku je števec in katera imenovalec?
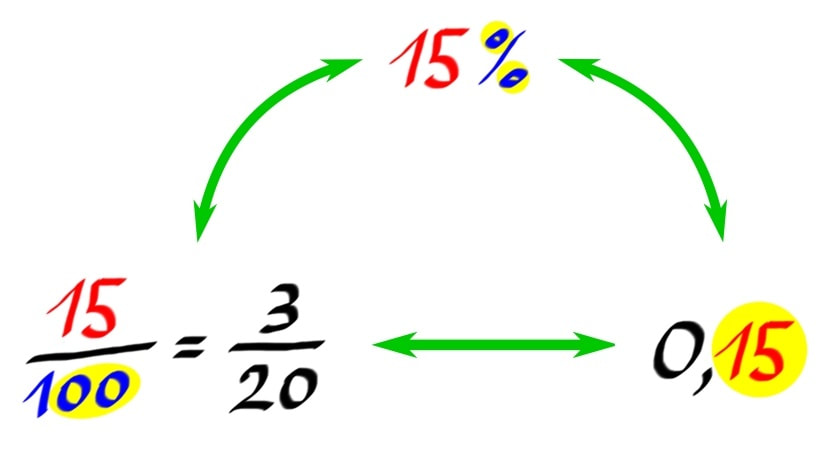
Števec spominja na štetje in je zgoraj, saj imamo eno tretjino, dve tretjini ... Imenovalec nas pa spominja na poimenovanje in je spodaj. Tako imamo eno tretjino, eno četrtino ... Recimo: "Pozdravljeni, ime mi je Petina in živim v spodnjem nadstropju ulomka." :) No, sedaj pri kontrolni nalogi sigurno ne boste več zamenjavali števca in imenovalca in na ta račun izgubili kakšne pomembne točke ;) Število lahko zapišemo v obliki ulomka, decimalnega zapisa ali pa z odstotkom. To še nekako vemo, ko pa je potrebno pretvarjati med zapisi, se pa rado zatakne.
Tukaj je nekaj napotkov:
Z Evklidovim algoritmom računamo največji skupni delitelj dveh naravnih števil. No ja...to lahko storimo tudi zelo preprosto - naredimo ulomek (eno število postavimo v števec, drugo v imenovalec) in ga okrajšamo. Naredimo primer za števili 180 in 210. Ko števili okrajšamo, dobimo ulomek šest sedmin: Če ulomek želimo razširiti nazaj, moramo števec in imenovalec pomnožiti z vsemi števili, s katerimi smo ga prej krajšali. V našem primeru so to števila 2, 3 in 5, njihov zmnožek pa je 30: S tem ugotovimo, da je 30 največji skupni delitelj števil 180 in 210.
Sedaj pa isti primer izračunajmo po Evklidovem algoritmu: 210 = 180 • 1 + 30 180 = 30 • 6 + 0 Za vse tiste, ki Evklidovega algoritma (še) ne poznate ali pa ste ga pozabili:
Sedaj pa se malo "poigrajmo" z zgornjim izračunom. Drugo vrstico iz zgornjega zapisa vstavimo v prvo (+0 ne pišemo): 210 = (30 • 6) • 1 + 30 180 = 30 • 6 + 0 Po ureditvi dobimo: 210 = 30 • 6 + 30 180 = 30 • 6 V obeh vrsticah izpostavimo, kar se da izpostaviti, v spodnjem računu pa tako ali tako nimamo kaj izpostavljati: 210 = 30 • (6 + 1) = 30 • 7 180 = 30 • 6 V obeh vrsticah smo izpostavili največji skupni delitelj števil 180 in 210, ki je 30. To pa je isto število, s katerim bi krajšali ulomek 180/210 (glej prvi primer). Naredimo še en primer, tokrat z nekoliko daljšim postopkom Evklidovega algoritma. Poiščimo največji skupni delitelj števil 80 in 36. 80 = 36 • 2 + 8 36 = 8 • 4 + 4 8 = 4 • 2 + 0 Zadnjo vrstico iz zgornjega zapisa vstavimo v prvo in drugo vrstico, drugo vrstico pa v prvo (+0 ne pišemo): 80 = (8 • 4 + 4) • 2 + 4 • 2 36 = (4 • 2) • 4 + 4 Po ureditvi dobimo: 80 = 8 • 4 • 2 + 4 • 2 + 4 • 2 36 = 2 • 4 • 4 + 4 V obeh vrsticah izpostavimo, kar se da izpostaviti: 80 = 4 • (2 • 8 + 2 + 2) = 4 • 20 36 = 4 • (2 • 4 +1) = 4 • 9 V obeh vrsticah smo izpostavili 4, ki je največji skupni delitelj števil 80 in 36. To pa je isto število, s katerim bi krajšali ulomek 80/36. Kaj pa če bi uporabili kar obe varianti, malo Evklidovega algoritma in malo krajšanja ulomkov? Števili zapišimo v števec in imenovalec ulomka tako, da bo njegova vrednost večja od ena, nato pa zapis pretvorimo v celi del + ulomek. Nazadnje ulomek okrajšajmo. V prvem primeru bi račun izgledal takole: 210/180 = 1 cela in 30/180 🡺 ker ulomek lahko okrajšamo s 30 (180 = 6•30), je 30 največji skupni delitelj števil 180 in 210. V drugem primeru pa: 80/36 = 2 celi in 8/36 🡺 ker ulomek lahko okrajšamo s 4 (8 = 2•4, 36 = 4•9), je 4 največji skupni delitelj števil 36 in 80. Zaključek: Evklidov algoritem je lahko zabavna igra s številkami, ki pa je v življenju ne potrebujemo prav pogosto (niti pri matematiki :)), zato gre kaj hitro v pozabo, medtem ko je krajšanje ulomkov vedno "na tapeti" - vsaj pri matematiki :) - in ga zlepa ne pozabimo. Pri seštevanju in odštevanju ulomkov je potrebno najti najmanjši skupni imenovalec (pri množenju in deljenju tega ne počnemo!) Teoretični način 1 - metoda iskanja najmanjšega skupnega večkratnika Ste vedeli, da je iskanje najmanjšega skupnega imenovalca v bistvu iskanje najmanjšega skupnega večkratnika? Dejansko vidimo, da je metoda za nekaj uporabna :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/30, 1/10 in 1/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa iz zgornjih vrstic "poberimo" praštevila, ki jih bomo uporabili v končnem izračunu. Pozor! Vsako nastopajoče praštevilo vzamemo le enkrat, razen če se le-to znotraj ene vrstice ponovi! V našem primeru se v zadnji vrstici ponovi 2, zato jo vzamemo dvakrat:
Ugotovimo, da je skupni imenovalec ulomkov 1/30, 1/10 in 1/20 enak
Primer 2: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Razstavljeni imenovalci so:
Dvojka se v drugi vrstici ponovi, zato jo vzamemo dvakrat, trojko pa enkrat:
Teoretični način 2 - metoda dopolnjevanja imenovalca do najmanjšega skupnega imenovalca Ta metoda je najprimernejša za razumevanje bistva najmanjšega skupnega imenovalca. Primer 1: Poiščimo skupni imenovalec ulomkov 5/30, 1/10 in 3/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa dopolnimo imenovalce z manjkajočimi faktorji - praštevili (množenje!) tako, da bodo vsi enaki:
Pozor! Vsako število, ki ga dodamo v imenovalec, moramo dodati tudi v števec! In ne pozabimo, med števili je znak za množenje! Sedaj imamo povsod v imenovalcu 2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 60. Račun z ulomki izgleda takole: Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 3/10 in 5/15. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 120. Račun z ulomki izgleda takole: Primer 3: Poiščimo skupni imenovalec ulomkov 1/3, 3/4 in 5/6. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*3, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 12. Račun z ulomki izgleda takole: Metoda je primerna tudi za računanje z izrazi: Primer 4: Izračunajmo naslednji račun. Če imenovalec tretjega ulomka zapišemo kot zmnožek dveh dvočlenikov, imamo situacijo zelo podobno situaciji v prvih treh primerih, le da tu namesto številk množimo dvočlenike v oklepajih. Lahko bi npr. množili tudi spremenljivke (črke: a,b,x,y,...). Imenovalca tretjega ulomka torej ne bomo zapisali kot zmnožek praštevil, ampak kot zmnožek dvočlenikov v oklepajih. Za dobro voljo: v tovrstnih matematičnih nalogah sta dvočlenika, ki ju dobimo z razstavljanjem enega od imenovalcev, ravno dvočlenika iz imenovalcev preostalih dveh ulomkov, tako da je taka naloga dokaj lahko rešljiva ;) No, tako je tudi v našem primeru: Dopolnimo imenovalce z manjkajočimi faktorji (dvočleniki v oklepajih) tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu (x+2)(x-3), kar pomeni, da smo našli najmanjši skupni imenovalec, to je (x+2)(x-3). Račun z ulomki izgleda takole: Način s poskušanjem 1: množenje in postopno deljenje
Načina s poskušanjem sta primerna za tiste, ki zadevo že nekoliko bolje obvladate :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. vse imenovalce zmnožimo med seboj:
72 je vsekakor skupni imenovalec 3, 4 in 6, ne vemo pa še, če je to najmanjši skupni imenovalec. Če se nam ne ljubi posameznih imenovalcev razstavljati na praštevila, lahko poskusimo s poskušanjem :) 72 delimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je še vedno skupni imenovalec vseh 3 števil v imenovalcih:
S poskušanjem smo ugotovili, da je najmanjši skupni imenovalec ulomkov 1/3, 1/4 in 1/6 število 12. Metoda z deljenjem je primernejša za manjše vrednosti imenovalcev, če so pa te večje, pa uporabimo lahko naslednjo: Način s poskušanjem 2: postopno množenje Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Poiščimo največji imenovalec (v našem primeru je to 6) in preverimo, če je mogoče deljiv z ostalimi imenovalci (v našem primeru sta to 3 in 4). Če je deljiv, je to že kar največji skupni imenovalec. Če ni deljiv, ga postopoma množimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je novo število deljivo z vsemi imenovalci. Kot ste opazili, je tudi to metoda s poskušanjem :)
Tole je bilo pa skorajda prelahko :) Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 1/10 in 1/15. Najprej preverimo, če je največji imenovalec (v našem primeru je to 15) deljiv z 8 in 10. Ker ni deljiv, ga moramo množiti s praštevili:
Primer 3: Poiščimo skupni imenovalec ulomkov 1/2, 1/3 in 1/6. Tu je največji izmed imenovalcev že kar največji skupni imenovalec. V tem primeru nam ga ni potrebno množiti s praštevili: Največji skupni imenovalec ulomkov 1/2, 1/3 in 1/6 je 6, saj je 6 deljiva tako z 2 kot s 3. Preprosto :) in sicer v dveh korakih:
Nekaj primerov:
To najlažje naredimo tako, da delimo števec z imenovalcem, saj ulomek v matematiki pomeni deljenje. Število s končnim decimalnim zapisom (po domače tako decimalno število, ki se ne "vleče" v neskončnost) pa dobimo samo, če ulomek razširimo tako, da v imenovalcu dobimo potenco števila 10 (po domače števila, ki ima spredaj 1, zadaj pa same ničle, npr. 10, 100, 1000,...) V število s končnim decimalnim zapisom lahko pretvorimo ulomek, ki ima v imenovalcu:
V število s končnim decimalnim zapisom pa ne moremo pretvoriti ulomkov, ki imajo v imenovalcu:
Pozor! če imenovalec množimo z nekim številom, moramo seveda z istim številom pomnožiti tudi števec, sicer bomo v godlji! :) Sedaj, ko imamo desetiški ulomek (v imenovalcu je potenca števila 10), le še:
Nekaj primerov:
|
ARHIV
May 2024
KATEGORIJE
All
|

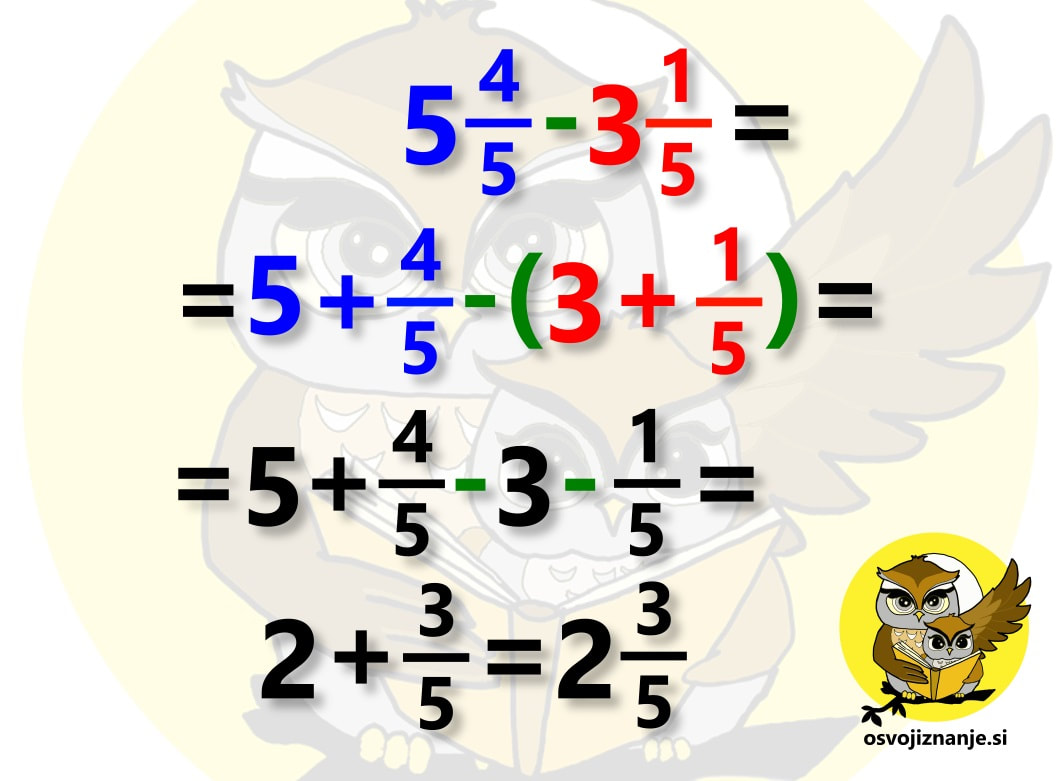




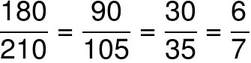
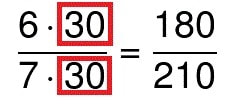
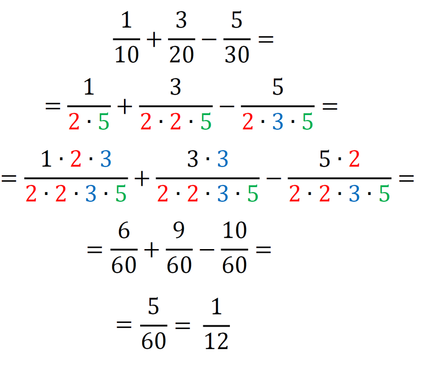
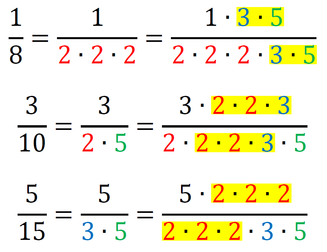
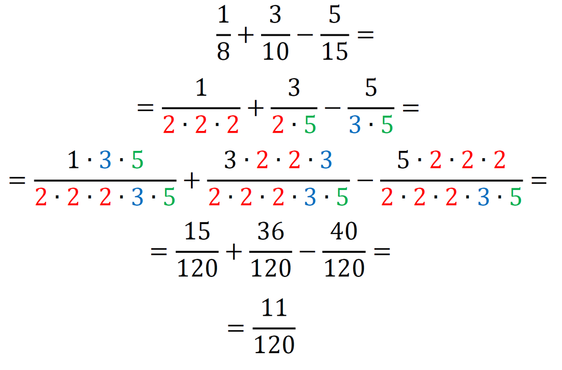
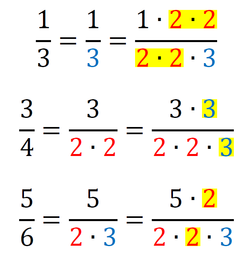
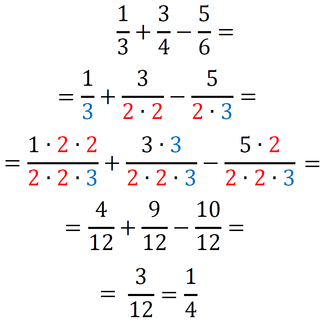
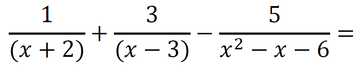
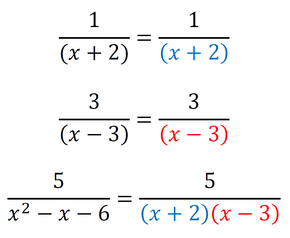
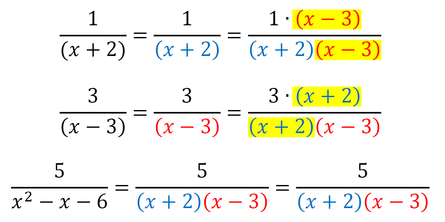
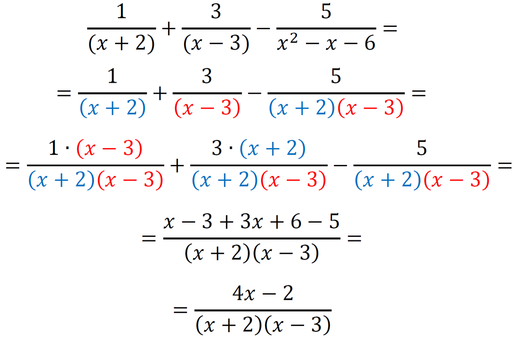
 RSS Feed
RSS Feed
