|
Z Evklidovim algoritmom računamo največji skupni delitelj dveh naravnih števil. No ja...to lahko storimo tudi zelo preprosto - naredimo ulomek (eno število postavimo v števec, drugo v imenovalec) in ga okrajšamo. Naredimo primer za števili 180 in 210. Ko števili okrajšamo, dobimo ulomek šest sedmin: Če ulomek želimo razširiti nazaj, moramo števec in imenovalec pomnožiti z vsemi števili, s katerimi smo ga prej krajšali. V našem primeru so to števila 2, 3 in 5, njihov zmnožek pa je 30: S tem ugotovimo, da je 30 največji skupni delitelj števil 180 in 210.
Sedaj pa isti primer izračunajmo po Evklidovem algoritmu: 210 = 180 • 1 + 30 180 = 30 • 6 + 0 Za vse tiste, ki Evklidovega algoritma (še) ne poznate ali pa ste ga pozabili:
Sedaj pa se malo "poigrajmo" z zgornjim izračunom. Drugo vrstico iz zgornjega zapisa vstavimo v prvo (+0 ne pišemo): 210 = (30 • 6) • 1 + 30 180 = 30 • 6 + 0 Po ureditvi dobimo: 210 = 30 • 6 + 30 180 = 30 • 6 V obeh vrsticah izpostavimo, kar se da izpostaviti, v spodnjem računu pa tako ali tako nimamo kaj izpostavljati: 210 = 30 • (6 + 1) = 30 • 7 180 = 30 • 6 V obeh vrsticah smo izpostavili največji skupni delitelj števil 180 in 210, ki je 30. To pa je isto število, s katerim bi krajšali ulomek 180/210 (glej prvi primer). Naredimo še en primer, tokrat z nekoliko daljšim postopkom Evklidovega algoritma. Poiščimo največji skupni delitelj števil 80 in 36. 80 = 36 • 2 + 8 36 = 8 • 4 + 4 8 = 4 • 2 + 0 Zadnjo vrstico iz zgornjega zapisa vstavimo v prvo in drugo vrstico, drugo vrstico pa v prvo (+0 ne pišemo): 80 = (8 • 4 + 4) • 2 + 4 • 2 36 = (4 • 2) • 4 + 4 Po ureditvi dobimo: 80 = 8 • 4 • 2 + 4 • 2 + 4 • 2 36 = 2 • 4 • 4 + 4 V obeh vrsticah izpostavimo, kar se da izpostaviti: 80 = 4 • (2 • 8 + 2 + 2) = 4 • 20 36 = 4 • (2 • 4 +1) = 4 • 9 V obeh vrsticah smo izpostavili 4, ki je največji skupni delitelj števil 80 in 36. To pa je isto število, s katerim bi krajšali ulomek 80/36. Kaj pa če bi uporabili kar obe varianti, malo Evklidovega algoritma in malo krajšanja ulomkov? Števili zapišimo v števec in imenovalec ulomka tako, da bo njegova vrednost večja od ena, nato pa zapis pretvorimo v celi del + ulomek. Nazadnje ulomek okrajšajmo. V prvem primeru bi račun izgledal takole: 210/180 = 1 cela in 30/180 🡺 ker ulomek lahko okrajšamo s 30 (180 = 6•30), je 30 največji skupni delitelj števil 180 in 210. V drugem primeru pa: 80/36 = 2 celi in 8/36 🡺 ker ulomek lahko okrajšamo s 4 (8 = 2•4, 36 = 4•9), je 4 največji skupni delitelj števil 36 in 80. Zaključek: Evklidov algoritem je lahko zabavna igra s številkami, ki pa je v življenju ne potrebujemo prav pogosto (niti pri matematiki :)), zato gre kaj hitro v pozabo, medtem ko je krajšanje ulomkov vedno "na tapeti" - vsaj pri matematiki :) - in ga zlepa ne pozabimo.
0 Comments
Leave a Reply. |
ARHIV
May 2024
KATEGORIJE
All
|
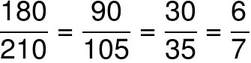
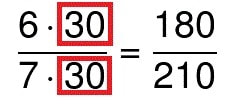
 RSS Feed
RSS Feed
