|
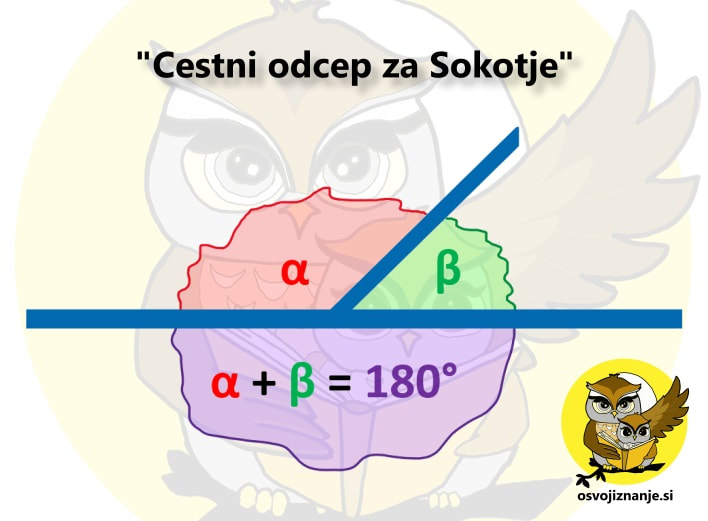
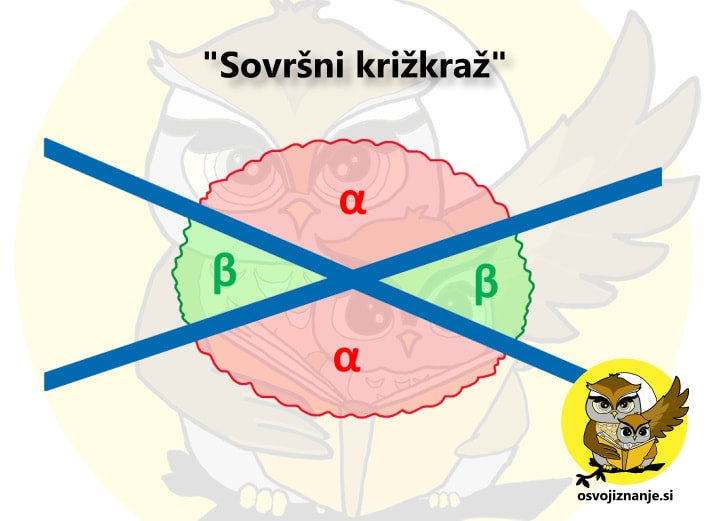
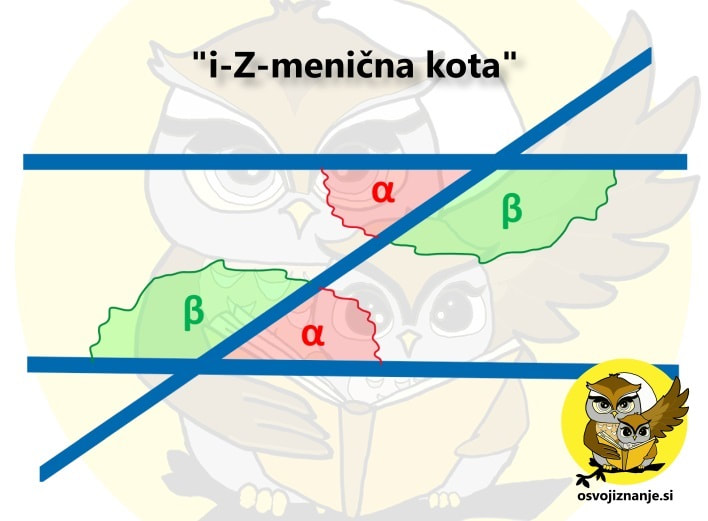
Koti radi nastopajo v paru, tudi v matematičnih testih. ;) Kdaj sta kota sokota in kdaj sovršna kota? Kaj pa izmenična kota? Čeprav se sliši zakomplicirano, si pojme zapomnimo veliko lažje, če si jih predstavljamo vizualno, zraven pa pripišemo še kakšno besedno zvezo. Temu se strokovno reče "dvojno kodiranje" (več o metodi učenja si lahko preberete v našem slovarčku). Mi imamo za vas nekaj predlogov, izmislite pa si seveda lahko tudi svoje. Ko govorimo o sokotih, si lahko predstavljamo ravno cesto z odcepom: Za sokota je značilno tudi to, da si delita en krak. No, ta krak je v našem primeru cestni krak :). Pri učenju sovršnih kotov si lahko predstavljamo »križkraž« ali črko x: Za sovršna kota je značilno tudi to, da si delita vrh, na kar lahko sklepamo že iz imena samega. Če seveda vemo, kaj je vrh kota. ;) Tudi tu se lahko znajdemo - če sta kraka nogi, je vrh kota lahko glava (saj se spomnite »glavonožcev«, ki smo jih risali v vrtcu? :) Pri izmeničnih kotih pa si zopet lahko pomagamo z abecedo, to je lahko črka Z ali pa črka N (kot nalašč obe najdemo tudi v imenu - iZmeNična kota): Ob pozornem pogledu na zadnjo sliko pa lahko opazimo tako sokote kot tudi sovršne kote. Kot je matematiki že običaj, je tudi tu vse povezano med seboj.
Zato kot že mnogokrat - ne učimo se matematike na pamet, ampak - po pameti! ;)
0 Comments
Pravijo, da slika pove več kot 1000 besed: Že res, ampak tule vam vseeno malo pomagam. ;)
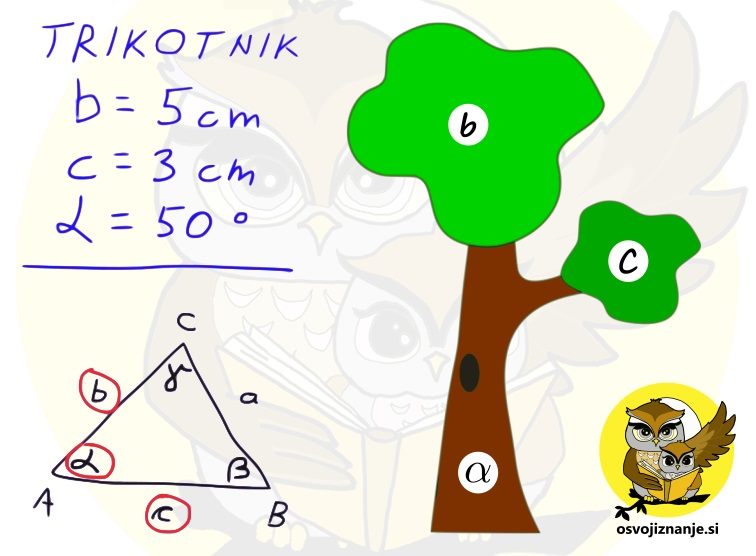
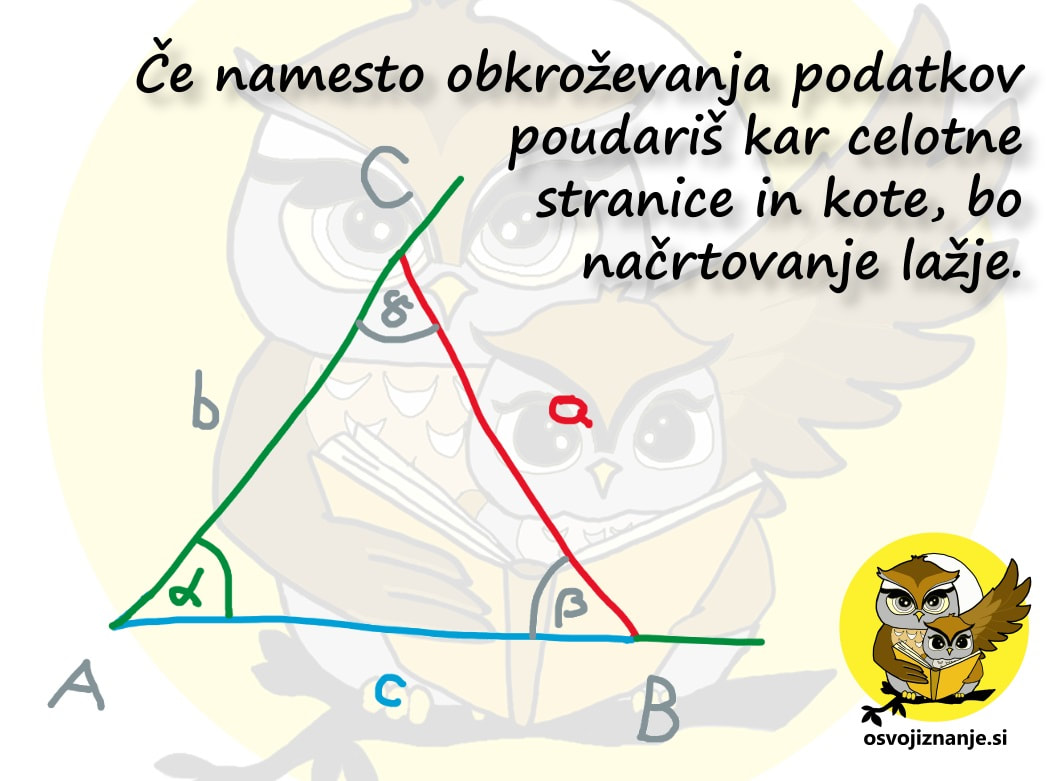
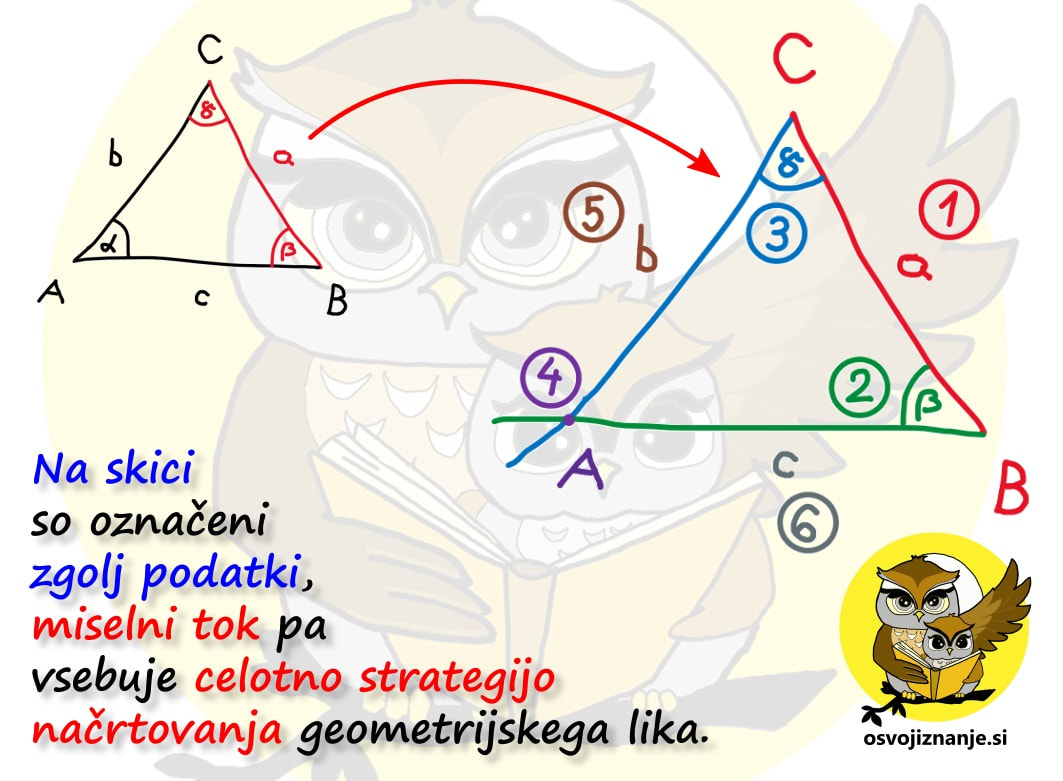
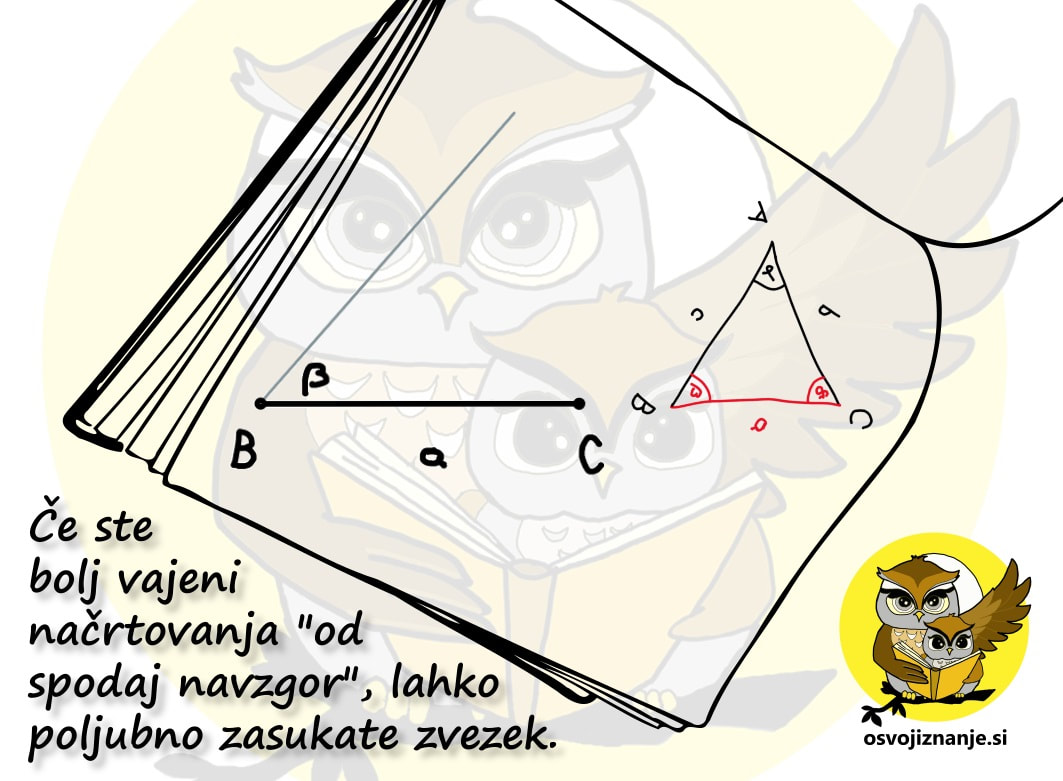
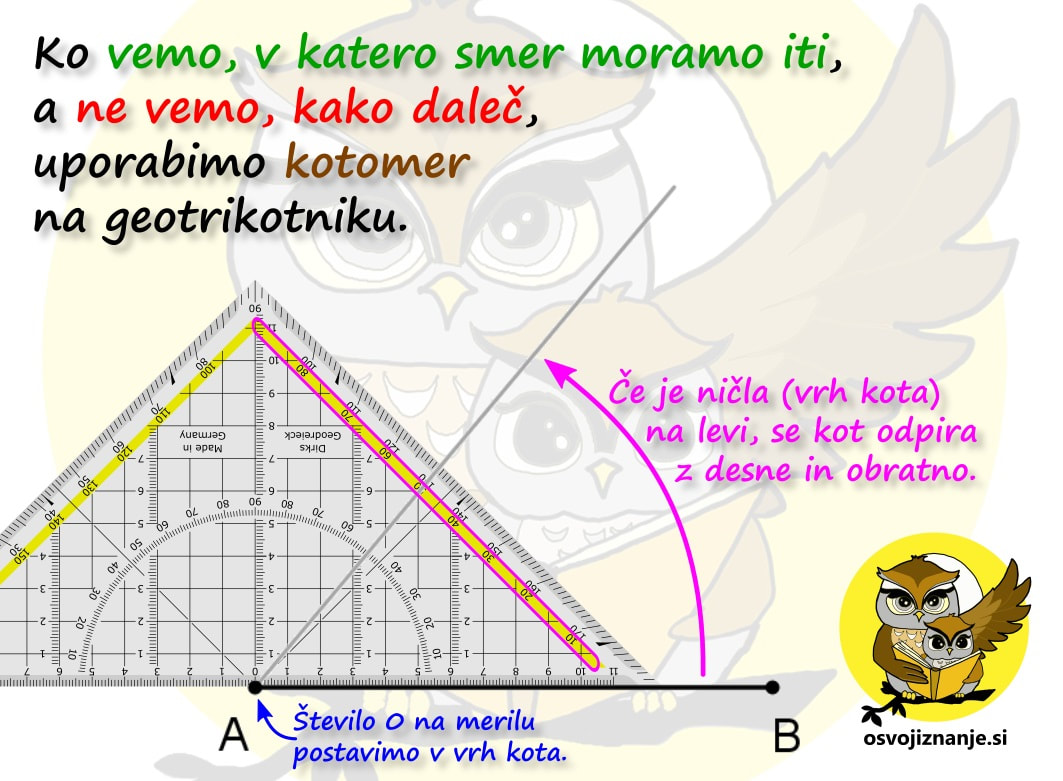
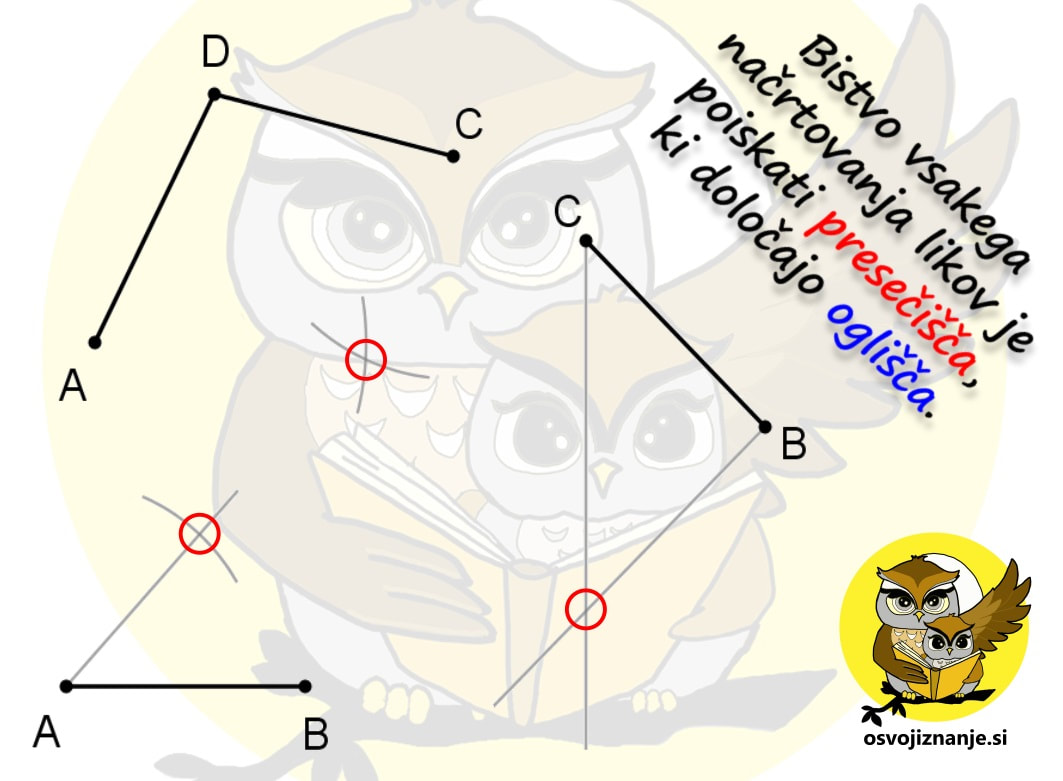
Slika predstavlja dokaj enostavni "recept" za načrtovanje geometrijskih likov, ki se glasi: "Najprej narišemo tisto, kar je vmes, nato pa še tisto, kar je na levi in na desni strani." V našem primeru pri trikotniku najprej narišemo kot alfa, nato pa na njem odmerimo še stranici c in b. "Logiko" si lahko zapomnimo s pomočjo drevesa. če hočemo priti do krošnje, moramo najprej splezati po deblu. ;) Imate tudi vi v zvezku na desetine navodil za načrtovanje geometrijskih likov »v stilu kuharskega recepta«? Potem pa končno izbrskate tako, ki »diši na podano nalogo«, začnete načrtovati in nekje na sredi ugotovite, da vendarle ni povsem »kompatibilno« z njo? Za take situacije sem pripravil neke vrste univerzalno navodilo, kjer najdete odgovor (skoraj) na vsako vprašanje v zvezi z načrtovanjem, ne glede na to za kakšen geometrijski lik gre. Mora biti na skici lik vedno enako označen? Ni važno, na kakšen način označimo sestavne dele, pomembno je le to, da se skice med načrtovanjem držimo. Kako na skici označiti poznane vrednosti (podatke)? Lahko jih obkrožimo, še bolje pa je na primer pobarvati kar celo stranico ali kote s kraki vred; te lahko tudi podaljšamo, da si bomo lažje ustvarili »miselni tok«. Kaj je to miselni tok? Z njim opišemo strategijo načrtovanja. Gre za neke vrste »drugo skico«, na kateri niso označeni le podatki, ampak predstavlja kar celoten, prostoročno narisan geometrijski lik. Bistvena sestavina miselnega toka pa so označeni koraki načrtovanja. Njegovo nastajanje si lahko predstavljamo kot neko generalko pred »ta pravim« načrtovanjem s šestilom in ravnilom. Ko načrtovanje enkrat že dovolj obvladamo, miselnega toka ni potrebno več risati, ampak je lahko zgolj »v glavi«. Ali pri načrtovanju lahko obrnem list? Seveda. :) Če si recimo navajen, da trikotnik začneš risati pri vodoravni stranici oziroma »od spodaj navzgor«, je to lahko tudi kakšna od poševnih stranic, le pravilno je potrebno zasukati list oziroma zvezek. Kje začeti z načrtovanjem? Najmanj dela imamo, če začnemo pri stranici. Če začnamo s kotom, je nekoliko več risanja, a imamo zato kasneje manj dela, saj imamo na sliki že več kot polovico trikotnika. Če imamo podano višino, lahko najprej narišemo »cesto« ... Kaj je naloga geotrikotnika? Z njim odmerimo točno določeno dolžino (ravnilo) in velikost kotov (kotomer). Katero merilo na kotomeru moramo gledati? Kot se "odpira" tako, kot se odpirajo vrata s tečaji v vrhu kota. Z odpiranjem kota se povečuje njegova velikost, s tem pa tudi številke na merilu kotomera. Uporabimo lahko tudi preprosto pravilo »kontra strani«: če je vrh na levi, se kot odpira z desne (povečevanje številk z desne) in obratno. Zakaj potrebujem šestilo? Z njim začrtamo, do kam bo segala daljica (stranica lika), katere dolžina je znana, a poznamo položaj je enega od njenih krajišč. V tem primeru »mero vzamemo« z geotrikotnikom, šestilo zapičimo v znano krajišče in začrtamo krožnico v smeri, v katero »sumimo«, da bo stranica potekala. Podobno kot pri iskanju ubežnika iz zapora ali zablodele živali. Kaj je bistvo vsakega načrtovanja geometrijskega lika? Glavna stvar, ki jo iščemo pri načrtovanju, so presečišča. Ko imamo vsa presečišča, ta samo še povežemo z ravnimi črtami in imamo lik. Presečišča dobimo bodisi s sekanjem krožnih lokov in/ali poltrakov. Prve na podlagi podatkov o dolžini daljic zarišemo s šestilom, druge pa na podlagi velikosti kotov z geotrikotnikom. Včasih nam kaj nikakor noče in noče "iti v glavo", zato se je potrebno spomniti kakšne "zvijače". Tu nikakor nimam v mislih kakšnega nelegalnega početja (plonkanje ...), pretentati je potrebno naše možgane :) Asociacije in kratke zgodbice so kot nalašč za to.
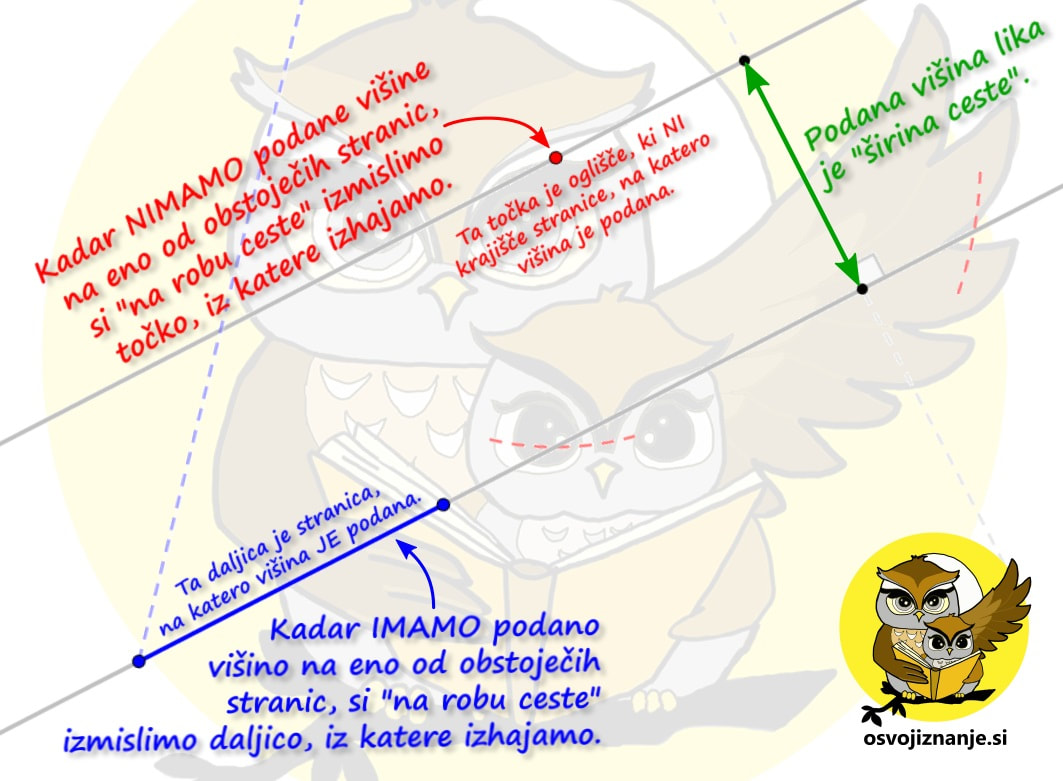
Premica ne more stati na točki oziroma premica ne more biti element na točki, tako kot se slon ne more usesti na muho :) Zato ne pišimo p ∈ A, ampak A ∈ p. Kaj dela mimobežnica? Beži mimo krožnice, kajpak :) Kaj pa dotikalnica? Ta se je pa dotika. Sekanta jo pa - seveda - seka. Kaj je razlika med sekanto in tetivo? Sekanta je ravna nitka, ki seka krožnico, tetivo pa dobimo, ko z ostrim rezilom (krožnico) odrežemo odvečna dela na levi in desni, tako kot pri krpanju nogavic :) Če imaš pri risanju geometrijskega lika nekje podano le dolžino neke stranice, ne pa tudi njene smeri, uporabi šestilo. Zamisli si, da stojiš na mestu, kamor zapičiš konico šestila, nato pa se z daljnogledom, ki "nese" do točno določene dolžine, ozreš na vse strani okoli sebe. Ni vrag, da v določeni smeri ne ugledaš iskanega cilja ;) Če imaš pri risanju geometrijskega lika podano višino, nariši cesto, katere širina je enaka višini. Pri risanju geometrijskega lika išči podatke, ki se "tiščijo skupaj". Zadeve bodo najbolj "pod kontrolo", če začneš pri podatku, ki je "v zlati sredini" :) No, pa razložimo tole zgodbico lepo in počasi :)
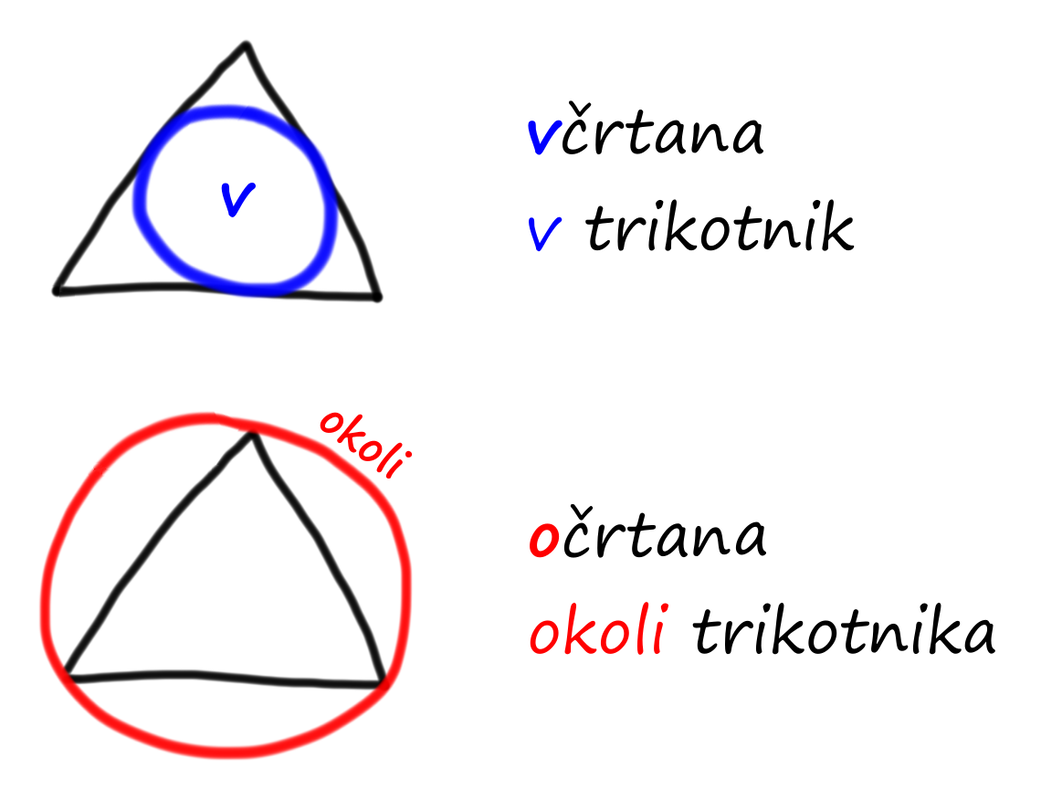
Enkrat je bila ena premica. Ime je dobila po tem, ker je bila revica vsa prema (po SSKJ: prema = ravna). Bila je svobodna. Segala je v eno in drugo smer v neskončnost. Potem pa je prišla od neznano kje ena točka in se je usedla nanjo, tako grdo, da jo je kar razpolovila. Na njenem mestu sta nastala dva poltraka, a nobeden od njiju ni bil povsem svoboden. V neskončnost sta se raztezala le v eno smer, medtem ko ju je na drugi strani omejevala - kdo drug kot grozna točka. Naša premica je pa imela sorodnico, ki se ji je pripetila nekoliko drugačna prigoda. Točke so imele prvenstvo v padalskih skokih. Med tekmovalkami sta bili tudi točka A in točka B. Sicer sta želeli pristati na isto mesto, a jima ni uspelo, tako da je bila med njima kar precejšnja razdalja. Omenjeno situacijo je slikal fotograf, ki je bil slučajno matematik in je sklenil, da bo del premice med točkama A in B poimenoval kar daljica. In še danes je tako. Ste bili kdaj v dilemi, kaj je potrebno narediti, če želimo dobiti središče trikotniku včrtane oziroma očrtane krožnice?
Tega se recimo že spomnimo, da je enkrat potrebno razpolavljati stranice, enkrat pa kote, ampak kdaj prvo in kdaj drugo? Zadeva v bistvu sploh ni tako zakomplicirana, kot se na prvi pogled zdi. Poskusimo za trenutek pozabiti na vsa matematična pravila in uporabimo le "zdravo pamet" :) Če želimo trikotniku narisati včrtano krožnico, mora le-ta biti vedno enako oddaljena od vseh treh stranic hkrati. Za začetek se osredotočimo samo na dve stranici. Znamo narisati niz točk, ki so vedno enako oddaljene od obeh stranic hkrati? Ker se stranici dotikata v oglišču, skupaj z njim tvorita kot. Niz točk, ki so enako oddaljene od obeh krakov kota pa verjetno poznamo, kajne? To je seveda simetrala kota :) Vsak sosednji par stranic skupaj z vmesnim ogliščem tvori kot (notranji kot trikotnika) in če vsakemu od teh kotov vrišemo simetralo, nam njihovo presečišče da središče včrtane krožnice. Narišemo pa potem to krožnico tudi povsem enostavno. Šestilo zapičimo v središče, z drugim delom le-tega pa se dotaknemo ene izmed stranic in narišemo krožnico. Kaj pa očrtana krožnica? Ta pa mora biti vedno enako oddaljena od vseh treh oglišč hkrati. Za začetek se osredotočimo samo na dve oglišči. Znamo narisati niz točk, ki so vedno enako oddaljene od obeh oglišč hkrati? Sosednji oglišči skupaj z vmesno stranico predstavljata daljico. Niz točk, ki so enako oddaljene od obeh krajišč daljice pa seveda poznamo - to je simetrala daljice :) Če vsaki od stranic vrišemo simetralo, nam njihovo presečišče da središče očrtane krožnice. Tudi to krožnico enostavno narišemo. Šestilo zapičimo v središče, z drugim delom le-tega pa se dotaknemo enega izmed oglišč in narišemo krožnico. Za konec povejmo še to, da je krožnico mogoče včrtati ali očrtati tudi mnogo drugim večkotnikom, ne le trikotniku. Več o tem pa najdete na Wikipediji. Marsikdo se pri nalogah z razreševanjem trikotnika znajde pred vprašanjem, kateri izrek uporabiti. Je to nemara sinusni, kosinusni, morda Pitagorov? Ali pa le kotne funkcije. Da se boste v tovrstnih situacijah lažje znašli, smo vam pripravili naslednji algoritem: Nekaj navodil za tolmačenje algoritma:
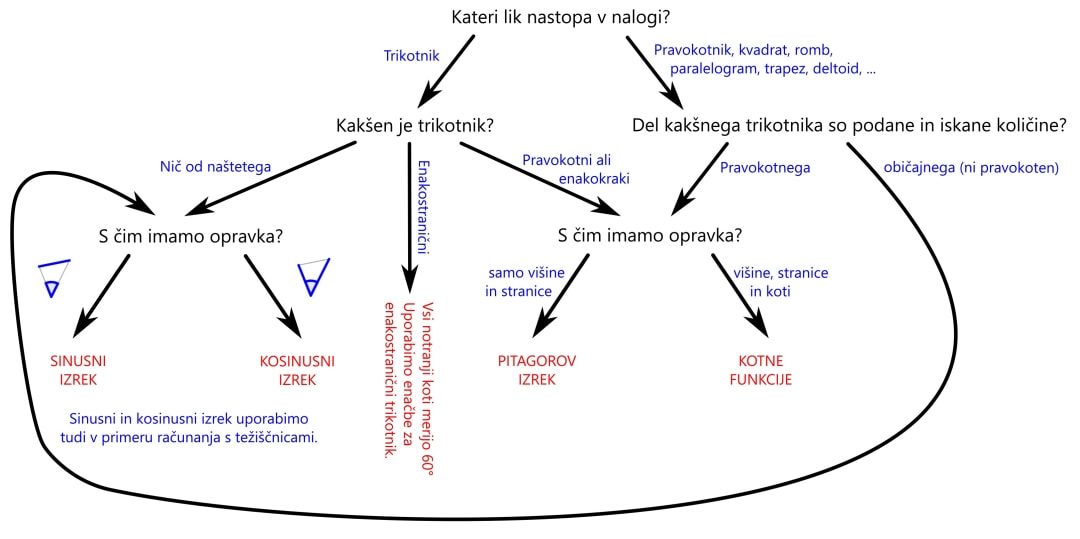
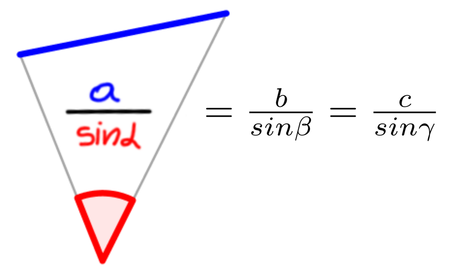
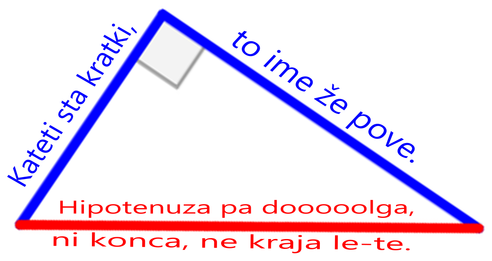
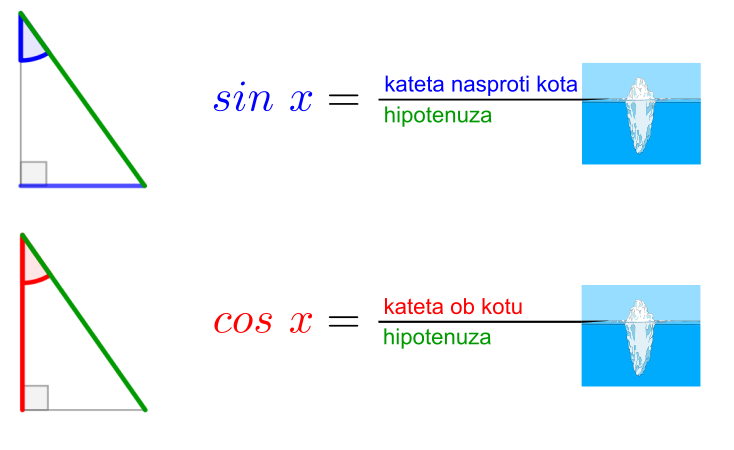
Sinusni izrek si lahko zapomnimo grafično ... ... ali pa s pomočjo verza: Če kot in stranica stojita SI Nasproti, trikotnika s SINusnim izrekom se loti! Tudi kosinusni izrek si lažje zapomnimo, če si ga narišemo ... ... ko pa nas misli popeljejo v naravo, si lahko barvno pudarjen del predstavljamo kot KOSov kljun :) Pitagorov izrek ni nič drugega kot posebna oblika kosinusnega izreka, ko je kot med stranicama na zgornji sliki enak 90° in obarvani del enačbe "pade", saj je cos 90° enak 0. Pomembno! Enačb se ne učite na stranico in kot določeno! Stranice so lahko označene z a, b in c, predstavljamo pa si jih praktično lahko kot karkoli ... recimo kot živali :) Kotnih funkcij se nam ni potrebno učiti vseh "na pamet". Preden povemo, kako to doseči, ponovimo razliko med katetami in hipotenuzo (to so stranice v pravokotnem trikotniku, če kdo slučajno še ne ve): Kateti sta kratki, to ime že pove. Hipotenuza pa dooooolga, ni konca, ne kraja le-te. Kotne funkcije so štiri (sinus, kosinus, tangens in kotangens), a "na pamet" se moramo naučiti le enačbi za prvi dve ... Če kot in kateta stojita SI Nasproti, SINus vržem v račun, ko pa hodita po isti poti, kosinus na to ne bo imun. Sinus in kosinus, kje je tu fora? Enačbi zanju sta kot ledena gora. Stranica krajša gor' in daljša dol', Ne en ne drug večji od 1 ne bo nikol'. ... medtem ko preostali dve kotni funkciji (tangens in kotangens) enostavno izpeljemo...ali pa kar zapojemo: 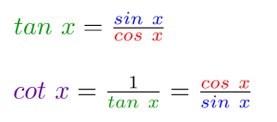 Enačbi za sinus in kosinus se naučim, za tangens pa kar prvega z drugim delim. Če pa kotangens koga zanima še, naj tangens na glavo obrne le. Zamislimo si, da bi morali po liku položiti parket - koliko kvadratnih metrov le-tega bomo potrebovali?
Če imamo podane razne polmere ter dolžine stranic in iščemo ploščino, računamo po "klasičnem" principu, brez obračanja enačb. Gremo po korakih:
Če imamo podano ploščino in iščemo polmere oziroma stranice, računamo po "obrnjenem" principu, z obračanjem enačb. Koraki (od točke 3 naprej) so v tem primeru nekoliko spremenjeni:
Zamislimo si, da bi morali po mejni črti lika napeljati ograjo - koliko metrov le-te bomo potrebovali?
Če imamo podane razne polmere ter dolžine stranic in iščemo obseg, računamo po "klasičnem" principu, brez obračanja enačb. Gremo po korakih:
Če imamo podan obseg in iščemo polmere oziroma stranice, računamo po "obrnjenem" principu, z obračanjem enačb. Koraki (od točke 5 naprej) so v tem primeru nekoliko spremenjeni:
Kdaj to lahko storimo? Naštejmo nekaj primerov:
Pri vseh zgoraj omenjenih primerih gre za premo sorazmerje. |
ARHIV
May 2024
KATEGORIJE
All
|



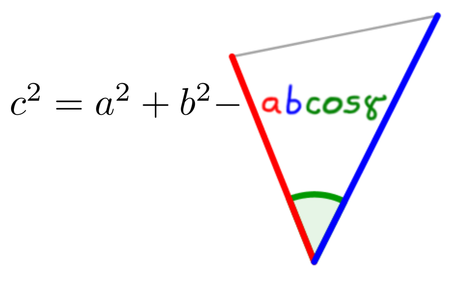
 RSS Feed
RSS Feed
