|
Pri množenju z 10 se decimalna vejica premakne za eno mesto v desno, pri deljenju z 10 pa za eno mesto v levo.
Kako si to najlažje zapomnimo? Preprosto. Premik decimalne vejice v desno pomeni povečanje vrednosti števila, saj ima celi del le-tega več števk, premik decimalne vejice v levo pa zmanjšanje vrednosti števila, saj ima celi del le-tega manj števk. Ker množenje s številom, večjim od 1 pomeni povečanje vrednosti, deljenje pa zmanjšanje le-te, je zadeva dokaj logična :)
0 Comments
V matematiki se velikokrat zgodi, da nekaj dejansko je tam, a tega ne vidimo ... in - papa točka ali dve pri kontrolki :( Matematika je sinonim za urejenost, zato mora pri zapisih vse "lepo izgledati", brez "odvečne krame" in med to "kramo" spada tudi nekaj predznakov in znakov za računske operacije. Lahko pa si zadevo predstavljamo tudi drugače, zamislimo si, da so matematiki le leni in se jim teh znakov enostavno ne da pisati :) Oglejmo si nekaj najznačilnejših primerov. Znak za množenje med spremenljivkami kljub temu, da znaka za množenje med spremenljivkami (črkami v računih) ne pišemo, moramo vedeti, da je tam. A pozor: Znak za množenje med številkami je nujen! Predznak + pred prvim členom v računskem izrazu Če pred prvim členom v računskem izrazu ni predznaka, to pomeni, da je le-ta pozitiven. A pozor! Če je prvi člen negativen, moramo predznak nujno zapisati! Katerega izmed faktorjev je potrebno postaviti nad in katerega pod ulomkovo črto? Vsi številski faktorji znotraj posameznega člena imajo levo od sebe znak za množenje ali deljenje. Glede na to tudi vemo, kam jih postavimo, če člen želimo zapisati v obliki ulomka. Množenje vodi v "zgornje nadstropje" (števec), deljenje pa v "spodnje nadstropje" (imenovalec ulomka) :) Posebnost pa je faktor na skrajni levi. Tega vedno zapišemo v števec ulomka. Zakaj? Oglejmo si primer na spodnji sliki. Levo od prvega številskega faktorja si predstavljajmo še en faktor - enico, s katero pomnožimo celoten člen (vrednost člena se pri tem seveda ne spremeni, saj množenje z 1 ne spremeni rezultata). Trojka tako predse dobi znak za množenje, kar jo "pelje" v števec ulomka. Enice pa v ulomku tako ali tako ni potrebno pisati (razen če bi bila edina v števcu ali imenovalcu). Pozor! Če je pred številskim faktorjem na skrajni levi slučajno predznak + ali -, ta ne vpliva na zgoraj povedano, saj se nanaša na celoten člen. Preprosto ga prepišemo pred ulomek. Kaj se nahaja med celim delom in ulomkom? Odvisno. Če gre za števila, je vmes plus. Če pa imamo spremenljivke (črke), je vmes krat. Ničle na skrajni levi in skrajni desni strani decimalnega zapisa Ničel levo od prve števke celega dela števila in desno od zadnje neničelne decimalke (števke v decimalnem delu števila) ne pišemo: Decimalna vejica pri celem številu?
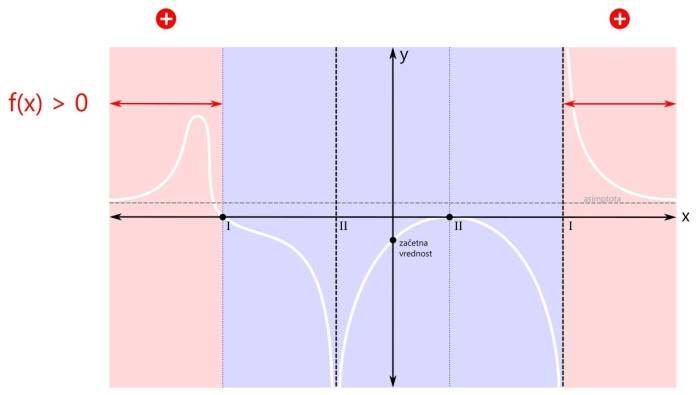
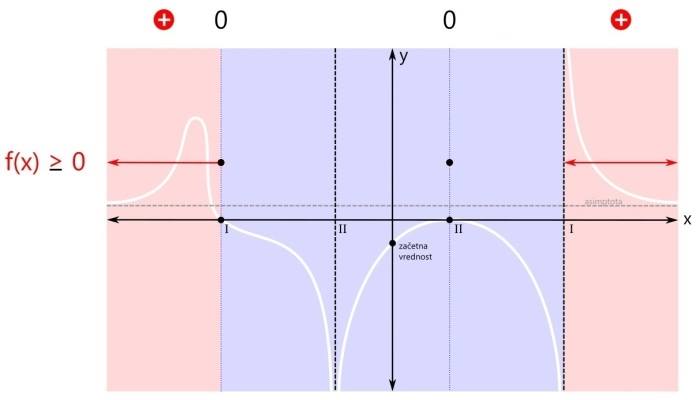
Celo število ne vsebuje decimalne vejice, je pa pri deljenju takega števila z večkratniki števila 10 dobro vedeti, "od kje pride". Vejica namreč "potrpežljivo čaka" na desni strani števke, ki v mestnovrednostnem konceptu predstavlja enico. Povezavo si oglejmo kar na primeru grafa racionalne funkcije, ki smo ga narisali tule. Ogledali si bomo štiri značilne primere. V prvem primeru je pogoj za neenačbo vrednost racionalne funkcije (strogo) večje od nič. Zakaj "strogo"? Zato, ker ničla ni dovoljena ampak velja samo tisto, kar je večje od nič. Pozor! Pogoj govori o vrednostih y, medtem ko rešitev neenačbe podajamo v vrednostih x! Rešitev neenačbe običajno podajamo v enem ali več intervalih. Ker pogoj zahteva vrednost funkcije, večjo od nič, se osredotočimo na pozitivna (rdeča) področja. Taki področji sta dve, zato bosta v rešitvi dva intervala. Na sliki sta označena z rdečimi črtami, ki imata na krajiščih puščici. Zakaj puščici? Puščici na intervalu označujeta, da krajišči intervala nista vključeni v rešitev. Če bi bilo kakšno krajišče intervala vključeno v rešitev, bi bila tam pika. Na splošno so na krajiščih puščice v naslednjih primerih:
Pozor! Kadar je pogoj za neenačbo "strog", se vam ni potrebno ukvarjati z zgoraj omenjenimi pravili, ampak si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervala še z oklepaji. Pri tem upoštevamo:
Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Med oklepaji je znak za unijo "∪". S tem znakom združimo intervale v eno rešitev. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desni pol pa na x=3, je v našem primeru rešitev naslednja: x ∈ (-∞,-3) ∪ (3,∞) V drugem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije večje ali enako nič. Od "strogega" pogoja se razlikuje v tem, da je ničla tu dovoljena. Tu pa nas zanimajo pozitivna (rdeča) področja ter ničle (črne pike):
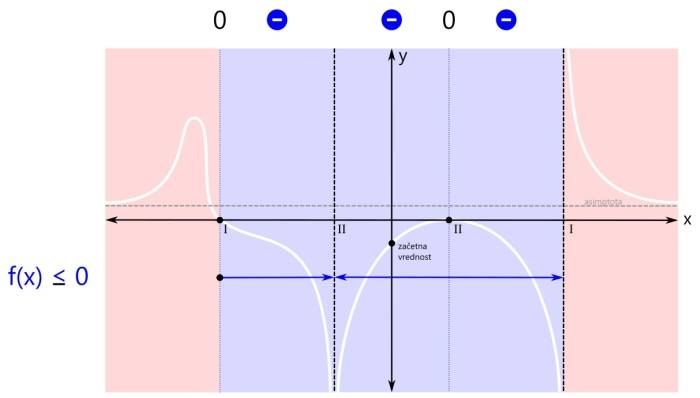
Ker sta rdeči področji dve, bosta v rešitvi dva intervala. Prva ničla (levo) je del prvega intervala (levo), zato je ni potrebno posebej navajati. Druga ničla (desno) pa je samostojna, zato jo je potrebno dodatno vključiti v rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desna ničla na poziciji x=1, desni pol pa na x=3, je rešitev naslednja: x ∈ (-∞,-3] ∪ {1} ∪ (3,∞) Pozor! Ker je rešitev v desni ničli le ena točka, je ne podamo kot interval, ampak kot zapis posameznega elementa množice rešitev - v zavitih oklepajih. V tretjem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije manjše ali enako nič. Tudi tu je ničla dovoljena. Kaj nas zanima? Negativna (modra) področja in ničle (črne pike):
Ker so modra področja tri, bi bili v rešitvi načeloma trije intervali, a ker desna ničla združuje dva od njih, bosta v rešitvi le dva intervala. Ničla na skrajni levi pa je tudi del "modrega" intervala, tako da je ni potrebno navajati kot ločeno rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desni pol pa na x=3, je rešitev naslednja: x ∈ [-3,-1) ∪ (-1,3) V zadnjem primeru neenačbe je pogoj vrednost racionalne funkcije (strogo) manjše od nič. Tako kot v prvem "strogem" primeru tudi tu ničla ni dovoljena. Velja samo tisto, kar je manjše od nič.
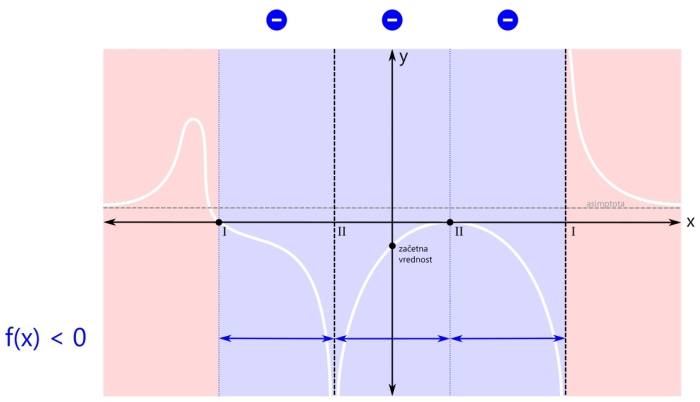
Ker pogoj zahteva vrednost funkcije, manjšo od nič, se osredotočimo na negativna (modra) področja. Tako področje je sicer eno samo, a je s polom in ničlo (druge stopnje) razdeljeno na tri dele. Rešitev bodo torej trije intervali. Na sliki so označeni z modrimi črtami, ki imajo na krajiščih puščice, kar pomeni, da krajišča intervalov niso vključena v rešitev. To, da so na krajiščih intervalov puščice in kdaj pike, smo že povedali, sedaj poudarimo samo naslednje: Pozor! Kadar je pogoj za neenačbo "strog", si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervale še z oklepaji. Ker imajo vsi intervali na krajiščih puščice, bodo vsi oklepaji okrogli. Še enkrat ponovimo naslednje splošno pravilo: Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desna ničla pa na x=1, je rešitev naslednja: x ∈ (-3,-1) ∪ (-1,1) ∪ (1,3) |
ARHIV
May 2024
KATEGORIJE
All
|



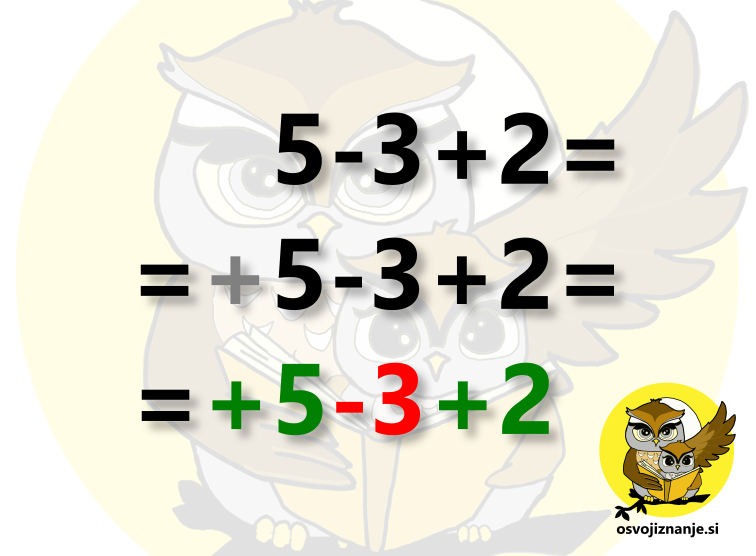

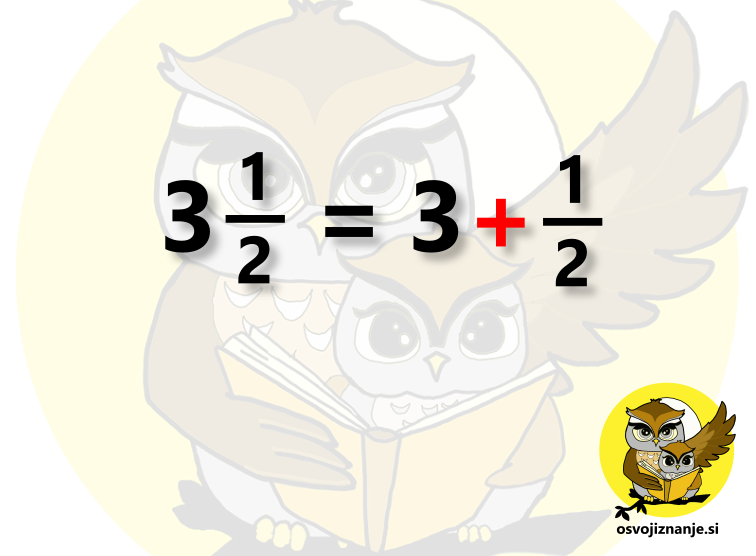
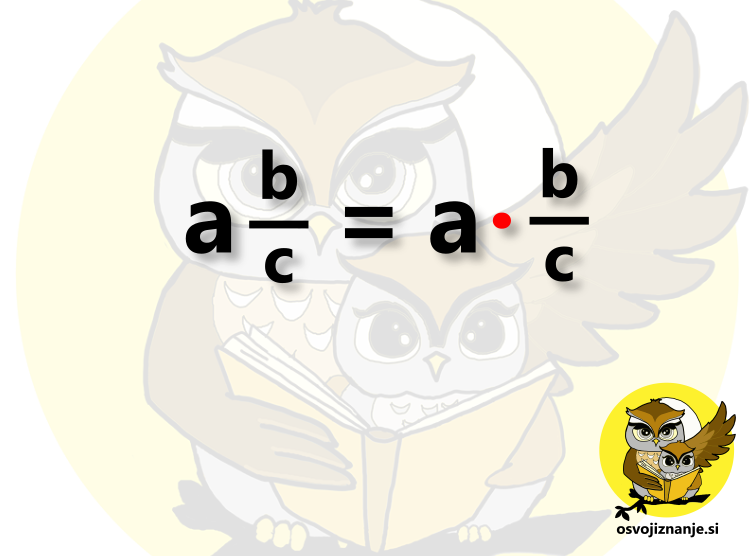



 RSS Feed
RSS Feed
