|
V nadaljevanju sledi nekaj nasvetov za reševanje nalog v stilu: "Zapiši množico točk, ki je predstavljena v koordinatnem sistemu..." Saj veste, ko imate na x/y "križkražu" polne in črtkane črte, pobarvano polje pa sega v neskončnost ali pa je stisnjeno v "sendvič"... :)
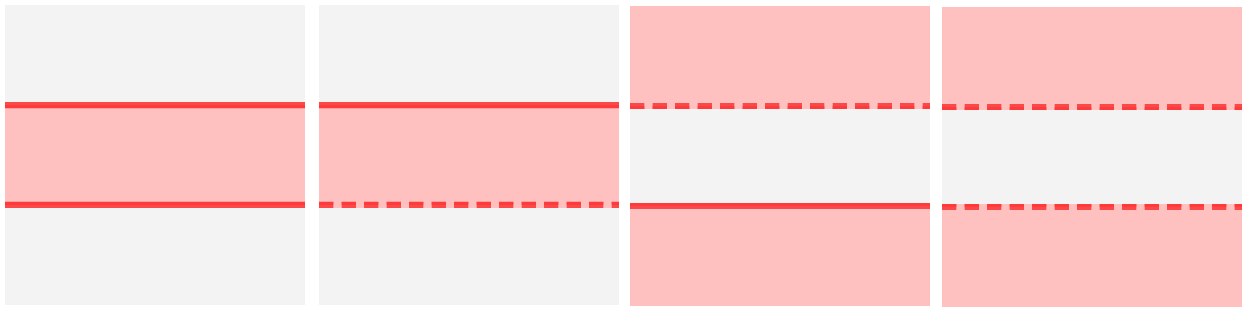
1. Na sliki je samo črta
2. Na sliki je črta, od katere se levo, desno, dol ali gor proti neskočnosti razteza pobarvano polje
3. Na sliki sta dve vzporedni črti, med katerima se razteza pobarvano polje (ujeto v "sendvič")
Oglejte si še legendo.
0 Comments
Saj poznate tiste naloge v stilu: "V koordinatnem sistemu nariši množico točk, ki ustreza zapisu..." In potem rišemo polne in črtkane črte, barvamo v neskončnost ali pa narišemo "sendvič"... :) Da se boste s takimi nalogami lažje spopadli, naj vam predlagamo naslednji "kuharski recept". 1a. Preverimo, ali pogoj velja za x os ali za y os (če je pogoj dvojni, preskočimo na točko 1b.) Tu bomo narisali eno vodoravno ali navpično črto.
1b. Preverimo, ali za x os ali za y os velja dvojni pogoj Tu bomo narisali dve vodoravni črti, dve navpični črti ali eno vodoravno in eno navpično črto.
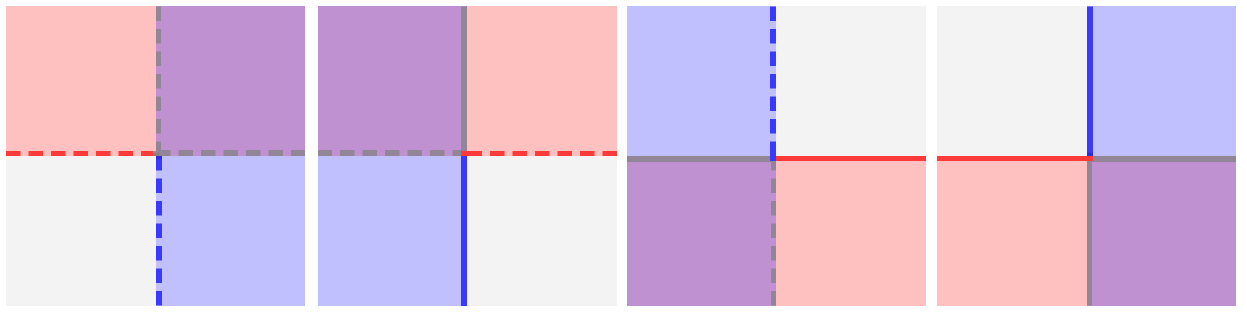
2a. Preverimo, za kakšen pogoj gre [>, <, ≥, ≤ ali =] (pri pogoju za x in y preskočimo na točko 2b): Tu barvamo levo/desno oziroma gor/dol od črte iz točke 1. Pri pogoju "=" ne barvamo ničesar. Če sta pogoja za x oziroma y dva, barvamo področje med črtama ali pa področje od črt navzven.
Tu barvamo levo/desno oziroma gor/dol od črt iz točke 1b (razen pri pogoju "=", kjer ne barvamo). Obarvani področji se prekrivata, kot rešitev pa velja naslednje:
Legenda:
Primeri slik za enojni pogoj za x (≤, <, =, >, ≥): Primeri slik za enojni pogoj za y (≤, <, =, >, ≥): Primeri slik za za dvojni pogoj za x: Primeri slik za dvojni pogoj za y: Primeri slik za pogoj za x in y (logični operator "in"): Primeri slik za pogoj za x in y (logični operator "ali"):
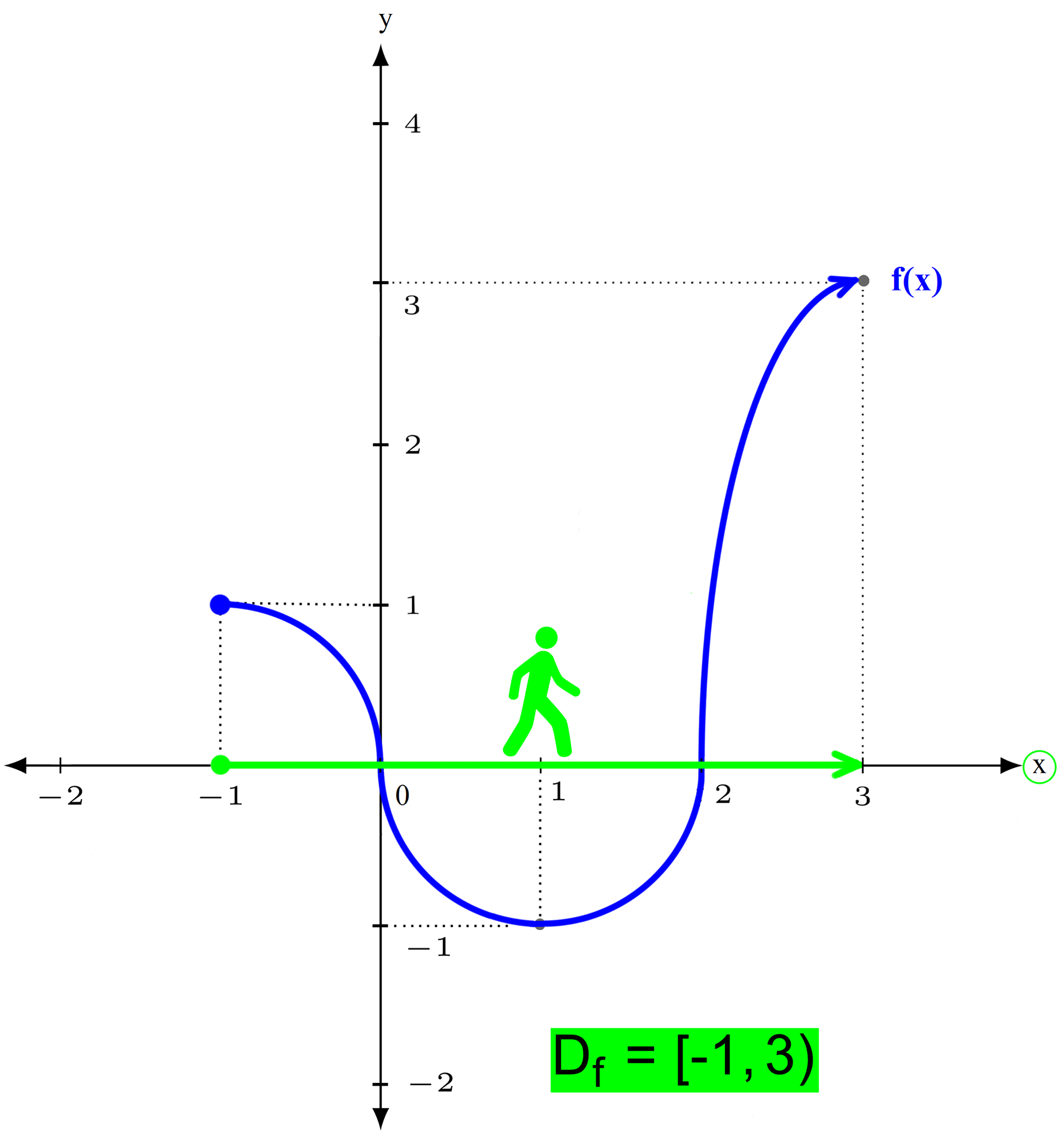
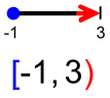
Ste se kdaj "zataknili" pri definicijskem območju ali zalogi vrednosti? Govorimo seveda o funkcijah, takih in drugačnih, vsaki z zvrhanim košem lastnosti :) Da pred tablo ali na pisnem testu ne boste "debelo gledali", vam predstavimo nekaj idej, kako funkciji določiti lastnosti na čim lažji način. Definicijsko območje Začnimo z definicijskim območjem, ki smo ga malo prej že omenili. Kot vemo, funkcija preslika neodvisno spremenljivko (največkrat je to x) v odvisno spremenljivko (običajno y). In definicijsko območje pomeni tiste vrednosti x, ki se bodo preslikale v y. Jap, ne pridejo vedno vse na vrsto za preslikavo ;) Definicijsko območje si je najlažje predstavljati na grafu funkcije. Zamislite si, da ste možak na spodnji sliki. Hodite po abscisi koordinatnega sistema (to je x os) od leve proti desni strani (v tej smeri tudi pišemo). Pri hoji se ozirate navzgor in navzdol, če boste kje videli funkcijo. Del poti, kjer je funkcija vidna, pobarvate z zeleno (tako kot je označeno na spodnji sliki). Interval, ki ste ga narisali (obarvan zeleno), je definicijsko območje funkcije:
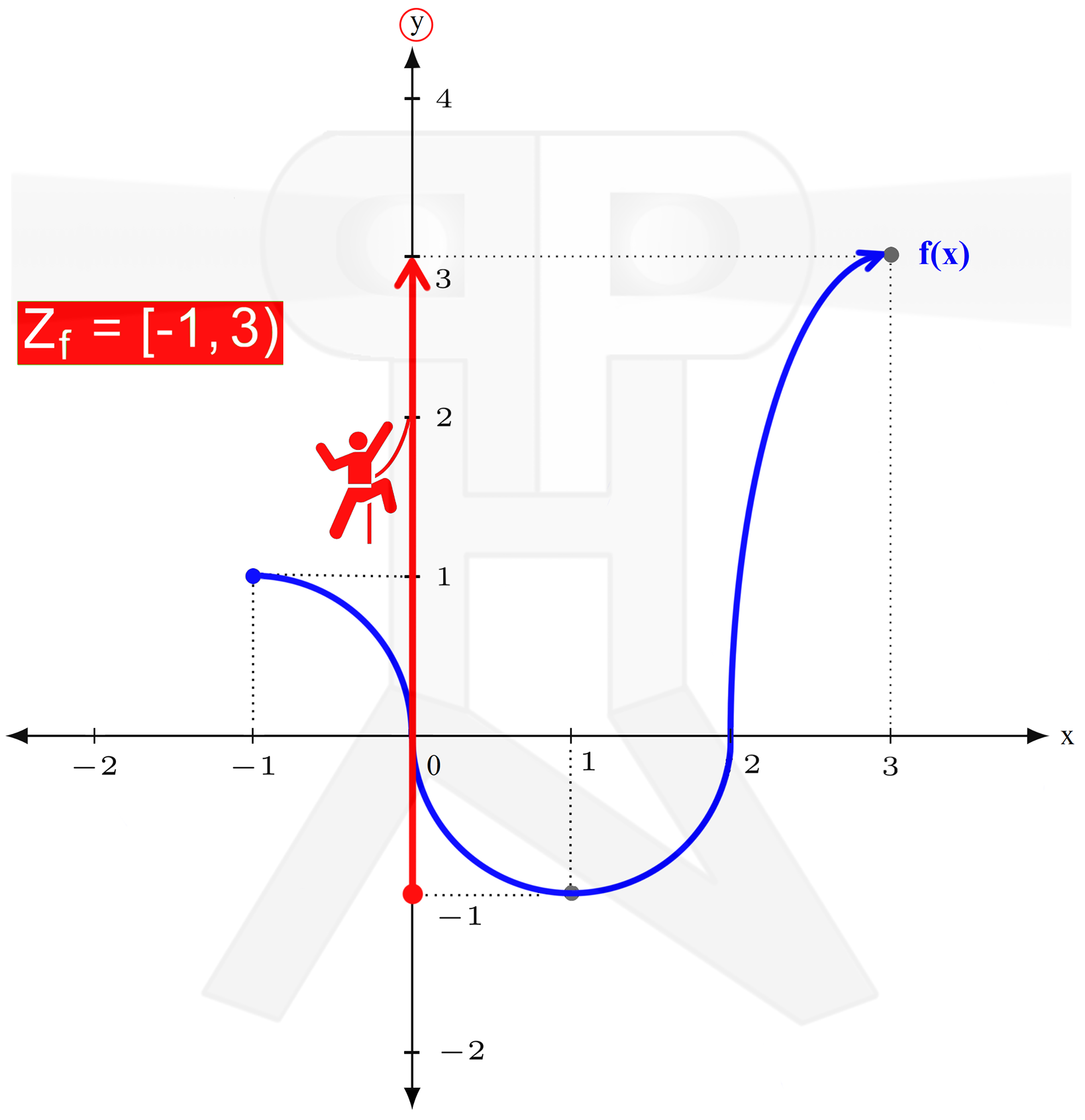
V našem primeru začetna točka spada zraven, končna pa ne. Temu primeren je tudi zapis definicijskega območja. Zaloga vrednosti Poleg definicijskega območja običajno vedno navedemo tudi zalogo vrednosti. Če so definicijsko območje tiste vrednosti x, ki se bodo preslikale v y, so "zaloga vrednosti" vse vrednosti y, ki so pri preslikavi nastale. Poenostavljeno bi lahko rekli, da se je definicijsko območje preslikalo v zalogo vrednosti. Tudi zalogo vrednosti si najlažje predstavljamo na grafu funkcije. V prejšnjem poglavju smo bili "zelen sprehajalec", sedaj pa bodimo "rdeč plezalec" ;) Včeraj smo hodili, danes pa plezamo, navpično navzgor, po ordinati koordinatnega sistema (y os). Plezati začnemo v najnižji točki grafa funkcije in splezamo vse do njenega vrha. Ker nam plezanje ne dela težav, zraven še malo pleskamo, tokrat z rdečo barvo :)
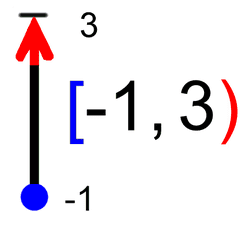
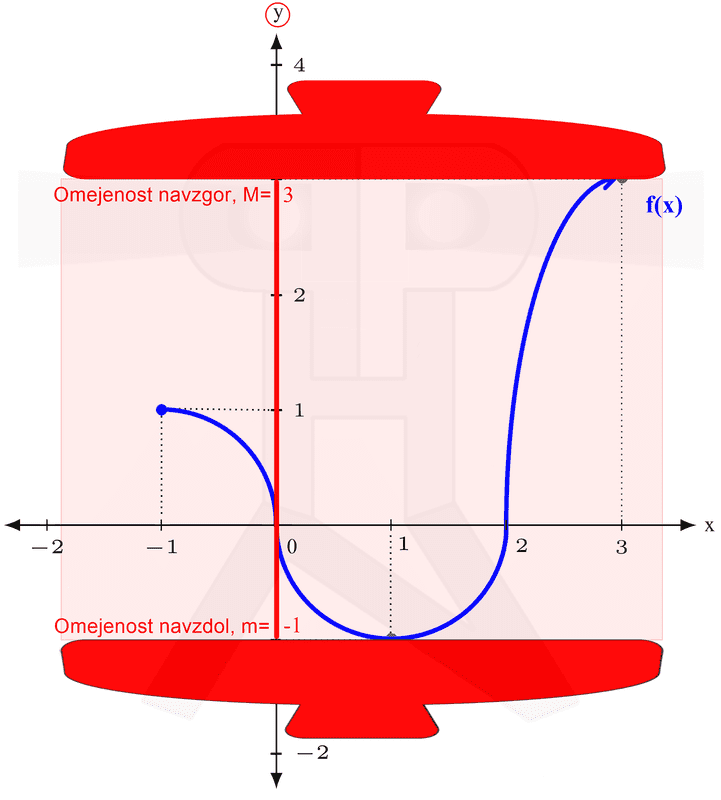
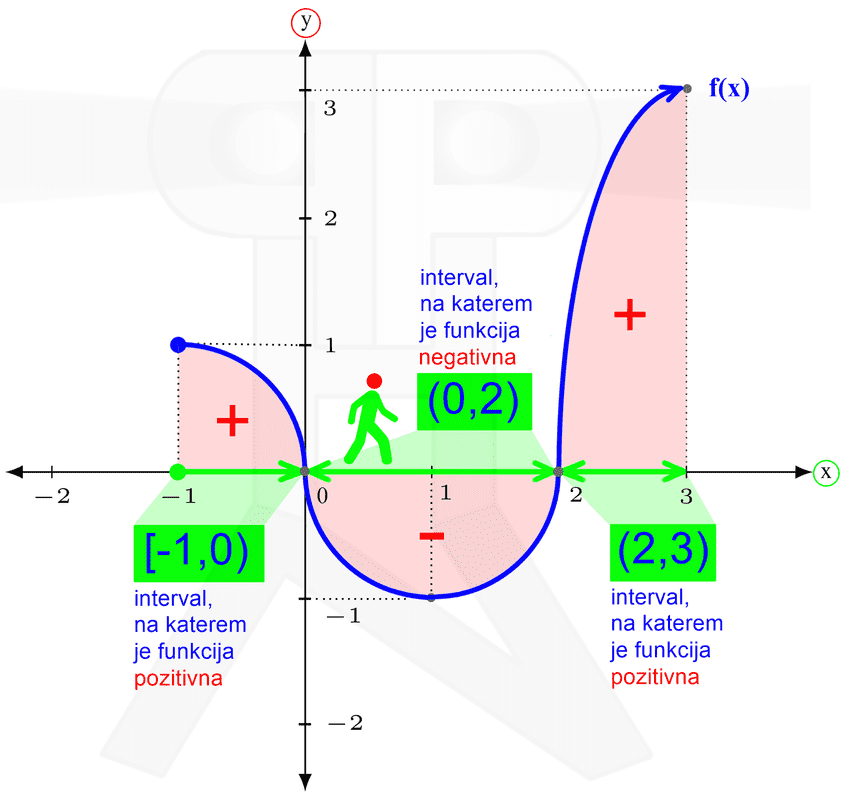
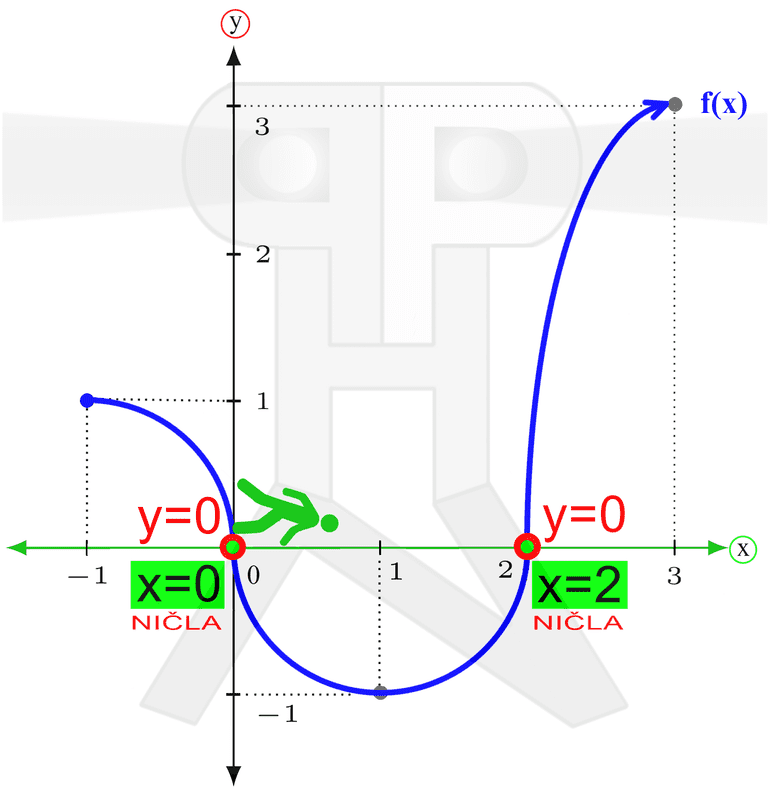
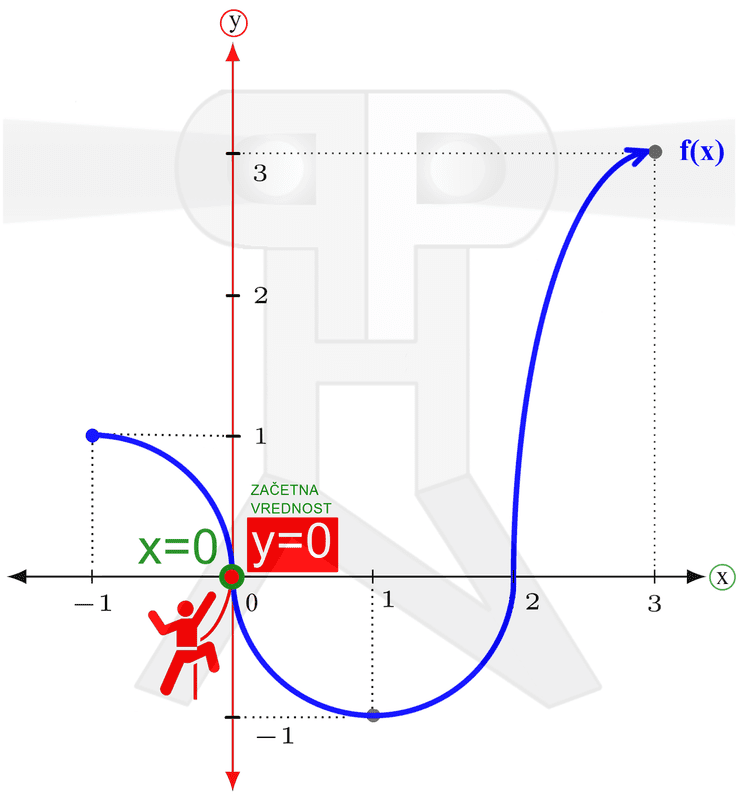
V našem primeru najnižja točka spada zraven, najvišja pa ne. Temu primeren je tudi zapis zaloge vrednosti. Naraščanje in padanje Na kratko: zanima nas, pri katerih vrednostih (neodvisne) spremenljivke x funkcija narašča in pri katerih vrednostih pada. Vrednosti spremenljivke x seveda ne naštevamo, ker bi jih bilo preveč, ampak jih podajamo v obliki intervalov. Spremenljivki x pripadajo "vodoravni" intervali, ki smo jih srečali že pri obravnavi definicijskega območja in so na naših slikah obarvani zeleno. Intervale naraščanja in padanja najlažje razberemo z grafa funkcije. Do sedaj smo tekli in plezali, tokrat pa se peljimo z avtomobilom. Peljemo se po (modri) krivulji funkcije od leve proti desni (v tej smeri tudi pišemo) in smo pozorni na to, ali se peljemo "v klanec" ali "s klanca". Ko gremo navzgor, funkcija narašča, ko gremo navzol, pa pada: Naj omenimo še to, da točke, kjer graf iz padanja preide v naraščanje (in obratno), ne spadajo v intervale naraščanja oz. padanja, zato so oklepaji v zapisu intervalov vedno okrogli. Ne pozabimo: če graf "pride iz neskončnosti" oziroma "gre v neskončnost", moramo pa tako ali tako uporabiti okrogli oklepaj! Omejenost Funkcija je lahko omejena navzgor, navzdol ali pa kar v obe smeri (in ne na levo in desno, kot se včasih kdo rad zmoti). Vsi ste že kdaj merili svojo višino. Če ne drugače, so vas izmerili na sistematskem pregledu. Na podoben način lahko "izmerimo" tudi funkcijo, s to razliko, da ne bomo podali njene višine, ampak le najnižjo in najvišjo točko. Zopet si pomagajmo z grafom funkcije. Zamislimo si dve veliki pokrovki (na sliki rdeče barve), med kateri "ulovimo" funkcijo. Zakaj ravno pokrovki? Zato, da bo zares "odbito" in si boste zato bolj zapomnili :) Položaj spodnje pokrovke na navpični (y) osi nam pove spodnjo mejo funkcije (označimo jo z malo črko m), položaj zgornje pokrovke na y osi pa nam pove zgornjo mejo funkcije (označimo jo z veliko črko M). Včasih se zgodi, da funkcije ne moremo "ujeti v pokrovko". V tem primeru funkcija navzdol oz. navzgor ni omejena. Kakšne niso omejene navzgor, druge navzdol, se pa najdejo tudi take, ki sploh niso omejene. Pozitivnost in negativnost Poglejmo, pri katerih vrednostih x je funkcija pozitivna oziroma negativna. Tudi tu vrednosti spremenljivke podajamo v obliki intervalov ("vodoravni" intervali, obarvani zeleno) Spomnimo se poglavja o definicijskem območju, kjer se je zelen možak oziral navzgor in navzdol ter preverjal, kje je funkcija vidna. Takrat ga ni zanimalo, ali je funkcija nad ali pod njim, sedaj pa je to pomembno (zato smo možaku glavo obarvali rdeče). Kadar je funkcija nad možakom, je le-ta pozitivna, kadar pa je pod njim, pa je negativna: Točke, kjer graf seka x os, ne spadajo v intervale pozitivnosti oz. negativnosti (uporabimo okrogli oklepaj!), saj tam funkcija ni ne pozitivna in ne negativna, ampak je njena vrednost enaka nič. Te točke imenujemo ničle funkcije. K njim se še vrnemo v nadaljevanju. Ne pozabimo: Če graf "pride iz neskončnosti" in/ali "gre v neskončnost", moramo na začetku prvega in/ali na koncu zadnjega intervala uporabiti okrogli oklepaj! Ničle funkcije Nekaj vrstic nazaj smo iskali vrednosti (neodvisne) spremenljivke x, pri katerih je funkcija pozitivna oziroma negativna. In kakšno vrednost ima funkcija, če ni niti pozitivna, niti negativna? Nič, seveda :) Točke, v katerih ima funkcija vrednost 0, imenujemo ničle funkcije. Nahajajo se na abscisni (x) osi koordinatnega sistema. Ne pozabimo: v ničlah je y enak 0, medtem ko vrednost "ničle" pove x! Na grafu ničle funkcije izgledajo kot neki kamni na zeleni poti (vodoravna x os), ob katere se spotika naš možic, ki smo ga že kar nekajkrat srečali: V ničli graf seka ali pa se dotika (zeleno označene) x osi. Graf seka x os v ničlah "lihega reda" (stopnje 1,3,5,...), dotika se ga pa v ničlah "sodega reda" (stopnje 2,4,6,...). V našem primeru sta ničli dve. Prva ima vrednost 0, druga pa vrednost 2. Označeni sta z zelenim okvirčkom. Začetna vrednost funkcije V nasprotju z ničlami, ki smo jih obravnavali nekaj vrstic višje, tokrat 0 ni vrednost funkcije, ampak vrednost neodvisne spremenljivke x. Ne pozabimo: v točki, ki označuje začetno vrednost, je x enak 0, medtem ko začetno vrednost podajamo z y! Na grafu začetna vrednost izgleda kot nek "oprijemek" na rdeči steni (navpična y os), po kateri pleza naš možic, ki smo ga že kar nekajkrat srečali: V tej točki, ki označuje začetno vrednost, graf funkcije seka (rdeče označeno) y os.
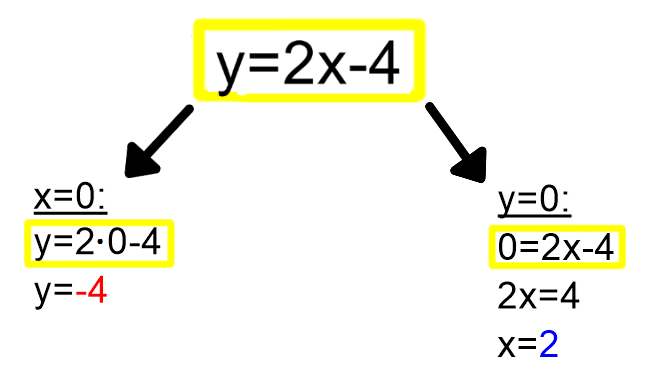
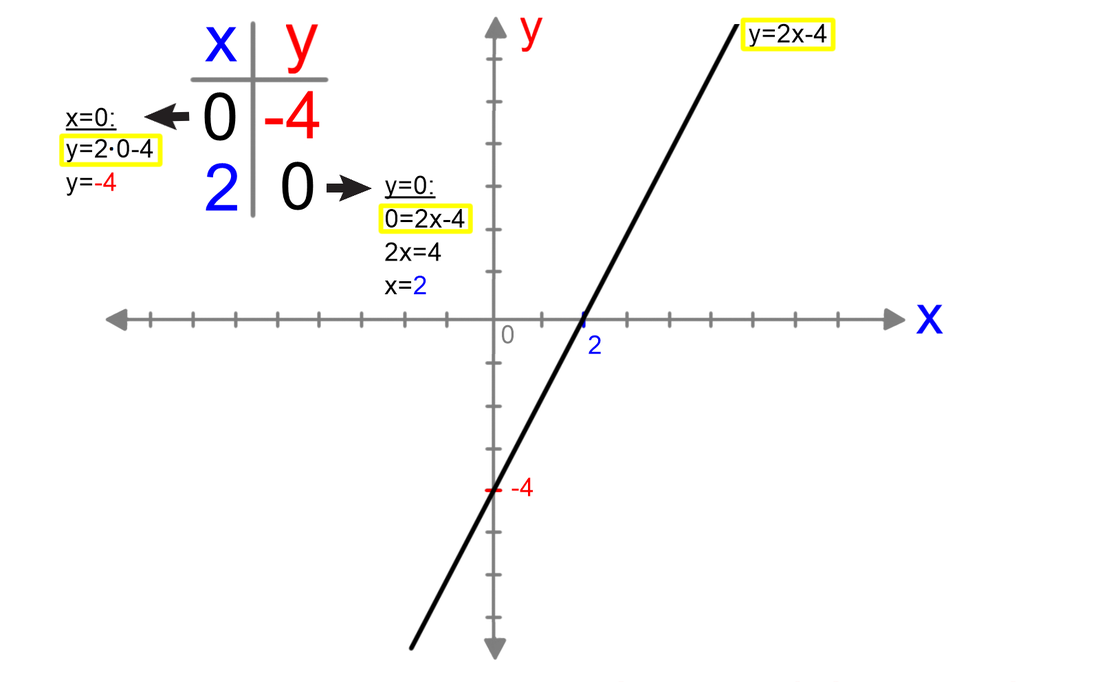
V našem primeru je začetna vrednost enaka 0. Označena je z rdečim okvirčkom. Načinov za risanje grafov linearnih funkcij je več; z enimi pokažete več znanja (ki ga tudi hitro pozabite), drugi so pa bolj enostavni, a jih zlepa ne pozabite. Pobliže poglejmo enega od slednjih. Narišimo graf linearne funkcije y=2x+4. Vemo, da ima linearna funkcija dve spremenljivki. Ena je neodvisna (x), druga pa je odvisna (y). Vse, kar morate storiti je, da vsako od njiju izenačite z nič in preverite, kakšno vrednost ima pri tem druga spremenljivka: S tem, ko smo vrednost spremenljivk x in y postavili na 0, smo dobili dve točki na koordinatnem sistemu. Ker imata vsaka eno od koordinat enako 0, ležita vsaka na eni od koordinatnih osi in ju je zato lahko označiti. Skoznji potegnemo le še premico in že imamo graf linearne funkcije. Naj na koncu opozorimo, da omenjena metoda ni primerna za grafe funkcij, ki potekajo skozi koordinatno izhodišče, saj v tem primeru omenjeni točki sovpadata (0,0).
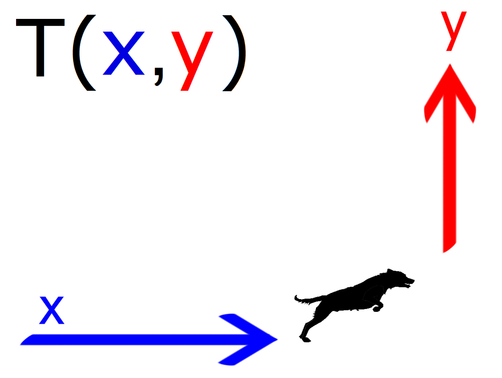
Iz težav nas reši tretja točka, katere koordinate dobimo tako, da si izberemo poljuben x (npr. 1), ga vstavimo v funkcijo in izračunamo vrednost y. Sedaj potegnemo le še premico skozi koordinatno izhodišče in to tretjo točko (1, izračunan y), in graf je tu. Zamislimo si psa, ki teče (od leve proti desni) in nato skoči. Tek psa je v vodoravni smeri. Vodoravna smer predstavlja x os na (kartezičnem) koordinatnem sistemu v ravnini. Skok psa je v navpični smeri. Navpična smer predstavlja y os na (kartezičnem) koordinatnem sistemu v ravnini. Sedaj pa logika: Pes mora najprej teči, da lahko skoči. Tudi x se v abecedi nahaja pred y. Torej je prva koordinata točke x, druga pa y: |
ARHIV
May 2024
KATEGORIJE
All
|




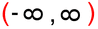

 RSS Feed
RSS Feed
