|
V šoli ste se verjetno učili o premem in obratnem sorazmerju. Potem ste se učili o odsotkih, razmerjih ...
Če si odstotke in razmerja (pa še kaj bi se našlo) predstavljamo kot premo sorazmerje, si razumevanje vsega skupaj lahko močno poenostavimo. Tudi reševanje takih nalog je zelo preprosto - kar preko sklepnega računa. Odstotki Pri računanju z odstotki imamo na eni strani odstotke, na drugi pa neke vrednosti (najraje denar :)). Ostotki in "tista druga" količina (denar, število ...) sta vedno v premem sorazmerju, saj več odstotkov vedno pomeni na primer več denarja. Pri odstotkih je pomembno vedeti, da je skupno število le-teh vedno enako 100. 100% na drugi strani ustreza skupni vrednosti "druge" količine, recimo seštevek vsega denarja. Primerjamo lahko različne odstotne vrednosti pod 100% med seboj ali pa posamezne vrednosti primerjamo proti celoti. Razmerja dolžin (daljic, stranic) v geometriji Vsi ste verjetno že zasledili nalogo v stilu "točka razdeli daljico v razmerju 2:3; koliko meri vsak del, če je celotna dolžina daljice ..." Prva količina v tem sorazmerju je del, druga pa recimo dolžina. Tudi tu je sorazmerje premo, saj večji del daljice recimo pomeni večjo dolžino. Tako kot lahko med seboj seštejemo posamezne dele, seštejemo tudi njihove vrednosti, recimo 2 in 3 je skupaj 5 delov, kar ustreza celotni dolžini daljice. Tudi tu lahko primerjamo posamezne dele med seboj ali pa proti celoti.
0 Comments
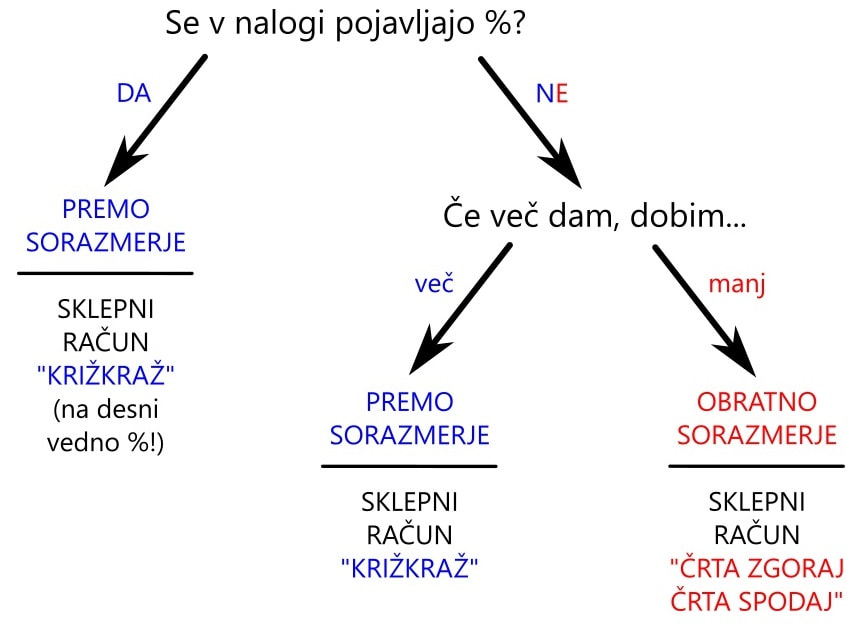
V šoli se verjetno sklepni in odstotni račun učite ločeno. Ko pride na vrsto preverjanje znanja, so pa naloge seveda pomešane. Da bi v množici nalog znali najti pravilni način reševanja, smo vam pripravili naslednji algoritem odločanja. Naj vas opozorimo, da pri opisanem postopku ne računamo s "klasično" odstotno enačbo, kjer nastopajo delež, relativni delež in osnova. Ta enačba je zelo "prikladna" za tiste, ki se učijo na pamet, a postane že ob prvi nekoliko bolj zapleteni nalogi popolnoma neuporabna. Zato vam bomo reševanje tekstnih nalog, tako z odstotki kot s sklepanjem, predstavili na enoten način - s starim, dobrim sklepnim računom. Algoritem izgleda takole: Na začetku se vedno vprašamo, če naloga vsebuje odstotke (procente). Če jih vsebuje, že takoj vemo, da gre za premo sorazmerje. Pripravimo tabelo: Legenda:
Pri tej tabeli je pomembno še:
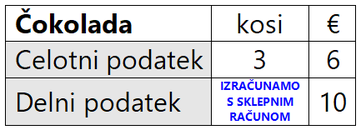
Posivljenih polj ne spreminjamo - so vedno enaka! Praktični primer: Če naloga ne vsebuje odstotkov, si zastavimo dodatno vprašanje: "Če več dam, dobim..." Na prvi pogled vprašanje izgleda nekoliko čudno, zato ga raje razložimo s praktičnima primeroma:
Pripravimo tabelo: Legenda:
Pri tej tabeli je pomembno še:
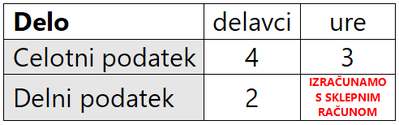
Posivljenih polj ne spreminjamo - so vedno enaka. Praktični primer za premo sorazmerje: Praktični primer za obratno sorazmerje: Opomba: Če se v nalogah pojavi več neznank, je potrebno za izračun vsake od teh nastaviti nov sklepni račun. Neznanke računamo po vrsti, z vsakim sklepnim računom eno.
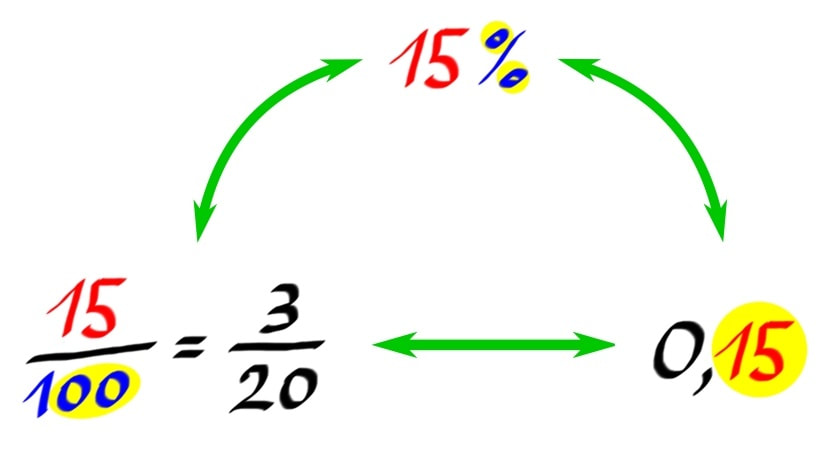
Število lahko zapišemo v obliki ulomka, decimalnega zapisa ali pa z odstotkom. To še nekako vemo, ko pa je potrebno pretvarjati med zapisi, se pa rado zatakne.
Tukaj je nekaj napotkov:
|
ARHIV
May 2024
KATEGORIJE
All
|



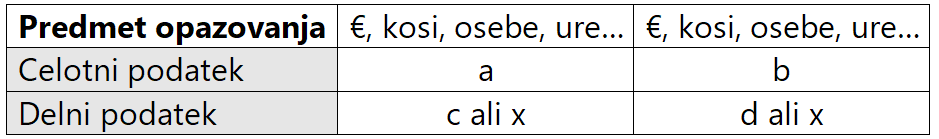
 RSS Feed
RSS Feed
