|
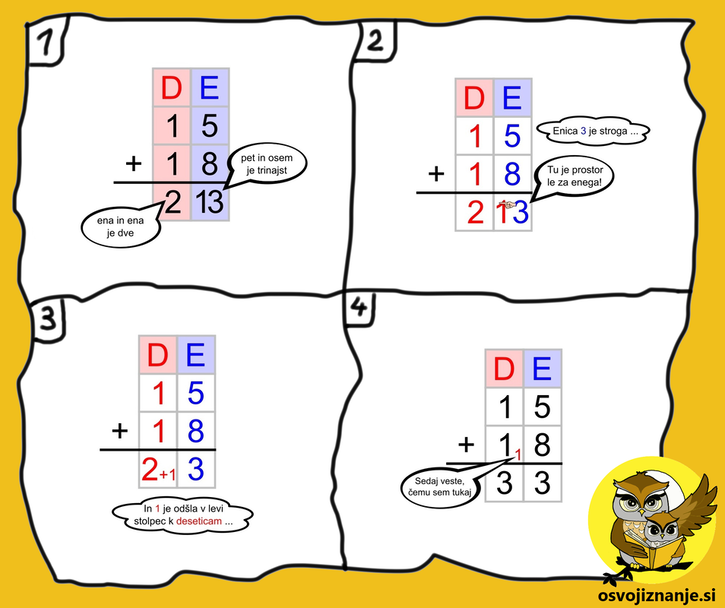
Pravijo, da slika pove več kot tisoč besed. Zato smo sklenili tole temo predstaviti kar v stripu. Prehod čez desetico zna biti trd oreh, če dogajanja pri tem "pojavu" ne razumemo povsem dobro, saj poznavanje le-tega igra odločilno vlogo tudi pri računanju z večjimi števili, tako pri seštevanju kot pri odštevanju. Pri prehodu čez desetico (tako kot tudi pri prehodu čez stotico, tisočico ...) je najpomembnejše dejstvo, da je v vsakem stolpcu (enic, desetic, stotic ...) na voljo le eno številsko mesto. Na tretji sličici vidimo, da desna števka ostane v "modrem" stolpcu enic, leva pa mora "na pot" v sosednji stolpec, k deseticam. V stripu je uporabljena enaka barvna koda, kot smo jo uporabili pri naši Čisti stotici (https://www.facebook.com/ucenjezigro).
Četrta sličica prikazuje "običajno stanje" v naših zvezkih (oziroma v zvezkih naših otrok, če to berete starši :) ). Marsikdo malo (rdečo) enko piše povsem avtomatično in se ne sprašuje, zakaj je tam, a ker v naših prispevkih spodbujamo kritično mišljenje, je dobro, da vemo, zakaj je tam in kako tja sploh pride. Razumevanje opisanega postopka je pomembno tudi zato, ker po seštevanju sledi odštevanje, kjer prehod čez desetico prav tako označujemo z malo številko na mestu desetice zadnjega seštevanca. Težava s prehodom čez desetico pri odštevanju je, da le-tega ne moremo prikazati analogno kot pri seštevanju, saj abstraktni postopek vizualni predstavitvi ne sledi popolnoma. Pri odštevanju namreč upoštevamo dejstvo, da je, karikirano, "razlika med 2 in 4 isto kot razlika med 3 in 5". Eno lažje narišemo, drugo pa izračunamo. In ker matematika ni likovna umetnost, upoštevamo dejstvo med narekovajema in se odločimo za slednjo možnost.
0 Comments
Čeprav se čudno sliši, je to povsem običajen postopek pri obračanju enačb, ko želimo izraziti iskano spremenljivko (običajno je to x). Pri tem si velja zapomniti dve glavni pravili: Prvo pravilo: Člen, ki ga ne potrebujemo (to je tisti člen, ki ne vsebuje iskane spremenljivke), preprosto "vržemo" na drugo stran enačbe, ob tem pa mu spremenimo predznak. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Pozitiven člen na levi strani enačaja postane negativen ... ... negativni pa pozitiven: Drugo pravilo: Ko imamo na levi (ali desni) strani enačbe le še tisti člen, ki vsebuje iskano spremenljivko, le-tega "razcepimo", tako da na tej strani enačbe ostane le še iskana spremenljivka, ostale faktorje pa prestavimo na drugo stran enačbe. Ob tem se prestavljenim faktorjem ne spremeni predznak, ampak položaj. Če so bili na eni strani v imenovalcu ulomka, so na drugi strani v števcu in obratno. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Faktor, pomnožen s spremenljivko x na levi strani enačaja, se na desni strani preseli v imenovalec ulomka ... ... faktor, ki je na levi strani enačaja v imenovalcu ulomka, pa na desni strani pomnožimo s preostalim delom enačbe: Pozor! Pri drugem pravilu moramo v primeru več členov na desni strani uporabiti oklepaj!
Primer: x/2 = 2a + b x = 2(2a+b) Poleg splošnega produkta različnih dvočlenikov ... (a+b)(c+d) ... sta pogosto v uporabi tudi posebna primera:
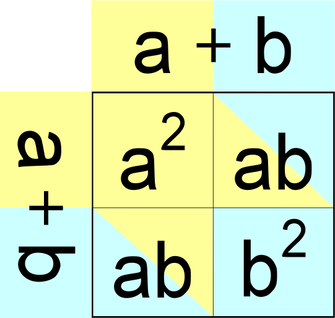
Enačbi za posebna primera je koristno poznati, saj ju potrebujemo pri razstavljanju. Za lažje pomnjenje si vse tri poglejmo v grafični obliki. Splošen produkt različnih dvočlenikov Enačba za splošen produkt različnih dvočlenikov se glasi: (a+b)(c+d) = ac+bc+ad+bd V grafični obliki enačba izgleda takole: Kvadrat dvočlenika Enačba za kvadrat dvočlenika se glasi: (a+b)² = a²+ab+ab+b² = a²+2ab+b² V grafični obliki enačba izgleda takole: Če je člen a ali b negativen, se predznak kvadratov (a² oziroma b²) ne spremeni, predznak srednjega člena (2ab) pa določimo po oranžnem pravilu množenja in deljenja:
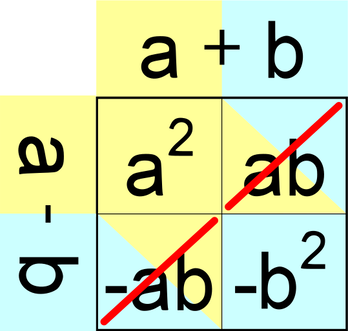
Produkt vsote in razlike enakih števil Enačba za produkt vsote in razlike enakih števil se glasi: (a+b)(a-b) = a²+ab-ab-b² = a²-b² V grafični obliki enačba izgleda takole: Na sliki se lepo vidi, da se srednja dva člena v računu okrajšata.
|
ARHIV
May 2024
KATEGORIJE
All
|
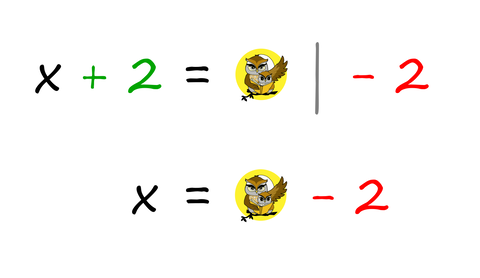
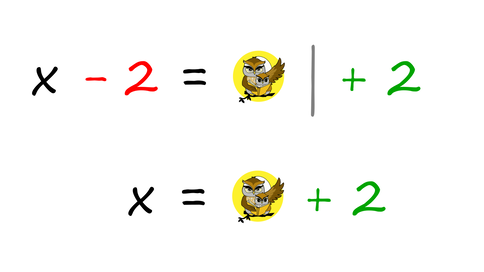
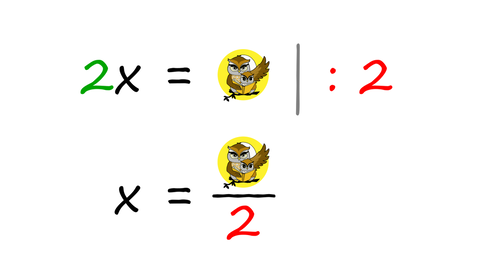
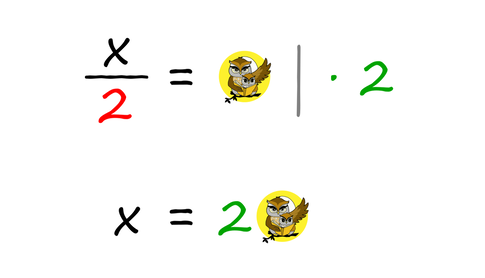
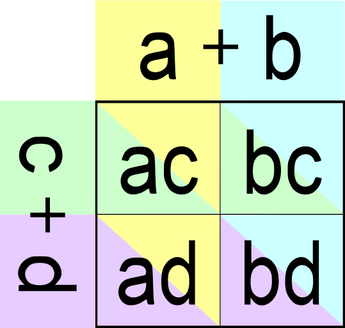
 RSS Feed
RSS Feed
