Zapletenka dneva #1: distributivnost

Distributivnost oziroma zakon o razčlenjevanju je lastnost množenja, da se lahko faktorji razčlenijo in posamezni členi teh faktorjev množijo.

Verjetno vam je zgornji stavek popolnoma jasen. Ne? Itak :)

Razložimo pojem bolj “po domače”.

Verjetno vas je večina že videla kakšen napovednik za prihajajoči film. Na koncu napovednika je običajno omenjen tudi distributer (npr. “Distribucija Karantanija Cinemas”). In kaj počne distributer? Distribuira filme, seveda :) No, da se ne boste izgubili med tujkami, najprej razložimo, kaj ta beseda sploh pomeni.

Po SSKJ distribucija pomeni razdeljevanje oz. razpošiljanje. Distributerji pa razdeljujejo, razpošiljajo… Filmski distributer razpošilja filme kinooperaterjem, obstajajo pa tudi drugi distributerji, recimo distributer plina, električne energije, bencina, prehrambenih izdelkov itd.

In kakšno zvezo ima filmska industrija z matematiko? Če ne drugega, oboji poznajo pojem distributivnost :) Če distributer distribuira, je distributivnost sama sposobnost distribucije. Joj, kakšen stavek! :) Preden vse skupaj do konca zavozlamo, si poglejmo praktičen primer.
​
Zamislimo si, da ima filmski distributer na mizi en kup filmskih kolutov, ki jih mora razposlati različnim kino operaterjem:

Najprej jih podolgem in počez razdeli (glej črte na spodnji sliki), nato pa razpošlje. Nekaj v Kolosej, nekaj v Cineplex in tako naprej. Vsak kinooperater ima svojo barvo kolutov:

In kje je tu distributivnost? Oglejmo si primer še z matematične plati.

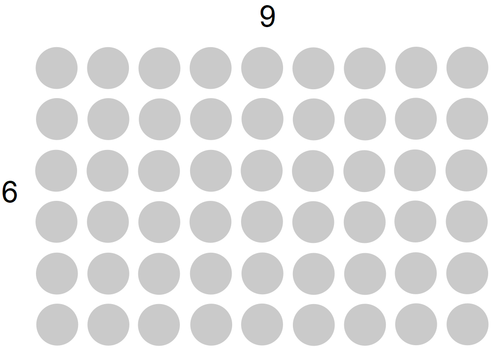
Iz prve slike s pomočjo znanja poštevanke hitro ugotovimo, da je kolutov 9•6, torej 54.

Na drugi sliki pa so naslednji koluti:

• 1•2=2 modra,
• 1•3=3 rdeči,
• 1•4=4 zeleni,
• 5•2=10 rumenih,
• 5•3=15 oranžnih in
• 5•4=20 roza.

Ker gre za iste kolute kot na prvi sliki, bi po logiki tudi teh moralo biti 54. S preprostim seštevanjem različnih barv ugotovimo, da naša trditev drži:

2 + 3 + 4 + 10 + 15 + 20 = 54

Vse lepo in prav, ampak še vedno ne vemo, kje je tu distributivnost. No, sedaj pa si že res zaslužite odgovor :)

V računu za prvo sliko (sivi koluti) imamo dva faktorja: 9 in 6.

Ker je množenje distributivno, lahko katerega koli od faktorjev razčlenimo na poljubno število členov (pretiravat pa vseeno ni treba). Mi smo razčlenili kar oba faktorja (glej drugo sliko): 

• 9 smo z navpičnima črtama razčlenili na 2, 3 in 4
• 6 pa smo z vodoravno črto razčlenili na 1 in 5.

Račun 9•6 je tako postal (2+3+4)(1+5).

Distributivnost oziroma zakon o razčlenjevanju nadalje pravi, da je sedaj potrebno posamezne člene zmnožiti med seboj. Saj poznate tisto: “Množimo vsakega z vsakim!” Naš račun se tako glasi:

9•6 = (2+3+4)(1+5) = 1•2 + 1•3 + 1•4 + 5•2 + 5•3 + 5•4 = 2 + 3 + 4 + 10 + 15 + 20 = 54

Mogoče se tole komu zdi brez veze, češ kaj pa kompliciramo, saj bi z znanjem osnovnošolske poštevanke enostavno zmnožili 9 in 6 ter dobili rezultat 54. V bistvu ni brez veze, le primer je nekoliko prelahek. Ampak saj primeri morajo biti lahki, da jih razumemo.

Poglejmo si še en primer. Zmnožimo števili 15 in 18. Tega se pa niste učili v osnovni šoli, ane? :)

S pomočjo distributivnosti račun 15•18 lahko preoblikujemo na raven osnovnošolske poštevanke, začinjene z nekaj seštevanja:

15•18 = (10+5)(10+8) = 10•10 + 10•8 + 5•10 + 5•8 = 100 + 80 + 50 + 40 = 270

Pa ne recite: "Ah, sej 'mamo kalkulator!" Možgančke je fino malo peljati na sprehod, da se ne zasedijo ;)