|
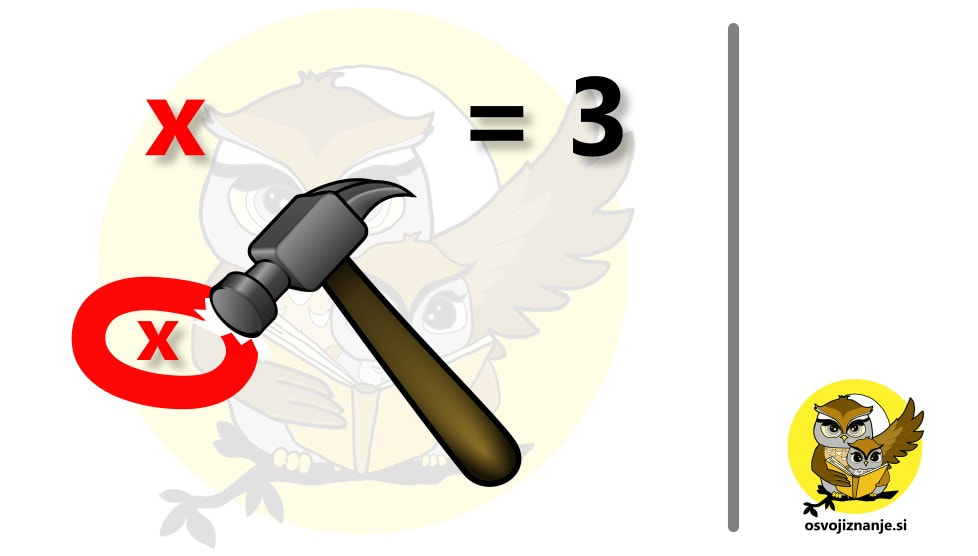
Prav ste slišali, kar s kladivom se je bomo lotili - metaforično seveda :) Omenjen pristop oziroma način razmišljanja utegne koristiti pri enačbah, ki vsebujejo "mešanico" osnovnih računskih operacij - vsaj eno seštevanje oziroma odštevanje ter vsaj eno množenje oziroma deljenje. Tak primer je recimo naslednja enačba: 3x + 2 - 6 = 5 Bistvo vsake enačbe je, da izrazimo oziroma "osvobodimo" neznanko, v našem primeru x. Če imamo preprosto enačbo, ki vsebuje le seštevanje in/ali odštevanje, preprosto uravnovesimo levo in desno stran tako, da bo na eni strani ostala le še neznanka. V našem primeru pa je neznanka pomnožena s faktorjem 3, zato bo potrebno za njeno "osvoboditev" nekoliko več napora. Osredotočimo se stran, ki vsebuje enačbo, v našem primeru na levo. Predstavljajmo si, da je ta izraz veriga: Naša veriga vsebuje 3 člene in kot nalašč, se tudi deli izraza na levi imenujejo členi. Po domače povedano, so členi "gmote" črk in/ali števil, ki so med seboj povezane s plusi in minusi. Več o členih si lahko preberete tule. Členi verige, ki ne vsebujejo iskane spremenljivke, so krhki in bodo odpadli najprej. Enačbo bomo rešili s postopkom istočasnega izvajanja računskih operacij na obeh straneh enačbe hkrati, ki je še najbolj pravilen način reševanja (t.i. "metanja" čez enačaj matematiki ne marajo preveč :) ). Pri tem si bomo pomagali z navpično črto na desni strani zvezka. Kar bomo pisali desno od te črte, si lahko predstavljamo kot komentar, ki nam bo prišel prav, ko bomo čez čas pregledovali svoje zapiske. Komentiranje je zelo razširjeno pri programiranju, še posebej, če programsko kodo piše več ljudi. Znebimo se najprej šestice. To storimo tako, da na obeh straneh enačbe prištejemo 6, saj je 6 na levi negativna (levo od nje stoji minus). 6 na levi tako nimamo več, na desni pa smo petici prišteli 6 in dobili 11. "Zelenega" člena na levi ni več, tako v računu, kot v verigi. Sedaj se znebimo še dvojke na levi, s tem, da na obeh straneh enačbe odštejemo 2, saj je 2 pozitivna (levo od nje stoji plus). Sedaj tudi 2 na levi nimamo več. Na desni pa smo 1 odšteli 2 in dobili 9. "Modrega" člena na levi ni več, tako v računu, kot v verigi, ostal je le še "rdeči" člen, ta, ki vsebuje iskano spremenljivko (x): Če iskano spremenljivko želimo "osvoboditi", moramo uporabiti kladivo :) V resnici ne bomo uporabili kladiva, želimo samo poudariti, da ima računska operacija deljenja, ki jo bomo sedaj izvedli na obeh straneh enačbe, večjo "moč" od seštevanja in odštevanja, ki smo ju izvedli v prejšnjih dveh korakih. Enako "moč" kot deljenje ima tudi množenje. In še nekaj zelo pomembnega: Orodje z največjo močjo uporabimo vedno na koncu. Tako kot v računalniških igricah ali pri kosilu - najboljše pustimo za konec :) Obe strani enačbe delimo s 3 in dobimo rezultat: To seveda ni univerzalen način reševanja enačb, si pa lahko z njim pomagamo pri "prvih korakih".
Mogoče kdo vpraša: "Kaj pa, če je neznanka v več členih?" V tem primeru pa take člene lahko združimo: 2x + 3x + 5 = 20 5x + 5 = 20 Seveda bi tudi našo enačbo lahko rešili hitreje; če nam negativna števila ne povzročajo težav, lahko zapišemo: 3x + 2 - 6 = 5 3x - 4 = 5
0 Comments
20 + ☐ - 10 = 40
Saj poznate tale tip naloge, kajne? :) Kako najlažje ugotoviti, kaj je potrebno vpisati v okvirček? Enačaj nam pri tem lahko močno pomaga. Kaj pomeni "je enako"? Dobesedno pomeni "je enako" :) In kaj je enako? Seštevek števil na levi in na desni. No, na desni nam niti računati ni potrebno, ker imamo le eno število :) Opomba: govora je o seštevku, števil na levi strani. Zraven seveda štejemo tudi odštevanje, ki je v bistvu prištevanje nasprotnih števil. Računali bomo torej le na levi strani. Zapišimo levo stran računa še "v barvah", da bo lažje razumljiv: 20 + ☐ - 10 = 40 Pri "barvanju" smo upoštevali, da znak za računsko operacijo vpliva na število, ki mu sledi (na desni) in ne na število pred njim oziroma (na levi). Več o tem si lahko preberete tule. Ljudje smo (večinoma) narejeni tako, da se najprej lotimo tistega, kar poznamo, šele nato pa neznanega. Tudi tu bomo naredili tako. Komur okvirček ni všeč, račun lahko zapiše tudi takole: 20 + ? - 10 = 40 "Naberimo" torej na levi strani skupaj tisto, kar poznamo ... 20 - 10 ... in izračunajmo: 20 - 10 = 10 Kaj nam je torej do sedaj uspelo narediti? Na levi strani smo združili znano in dobili: 10 + ☐ = 40 Tole je pa že kanček lažje, kajne? :) Zopet se spomnimo na enačaj, ki nam pove, da mora biti rezultat na levi strani enak rezultatu na desni. Če imamo na levi strani 10, na desni pa 40, nam na levi nekaj manjka. Koliko moramo torej dodati na levi strani, da dobimo isto, kot imamo na desni? Odgovor je 30, saj velja 10 + 30 = 40 Opomba: Sklepali bi lahko tudi, da imamo na desni strani 30 preveč, kar je sicer pravilno, a potem računa ne bi mogli rešiti, saj se okvirček nahaja na levi in ne na desni strani. V okvirček tako zapišemo 30 in celoten račun se glasi: 20 + 30 - 10 = 40 Če naredimo preizkus, na levi strani res dobimo 40. Še nasvet za konec: Namesto (abstraktnih) števil lahko pri enačenju uporabimo tudi konkretne pripomočke - štejemo kocke, kroglice, denar ... ali pa tehtamo. Ulomkov marsikdo ne mara, delno tudi zato, ker jih v izrazih ne moremo preprosto seštevati in odštevati, ampak jih moramo prej vedno razširiti na najmanjši skupni imenovalec: Nekoliko raje jih imamo v enačbah. Tu nam ulomkov ni potrebno razširjati na najmanjši skupni imenovalec, ampak z njim preprosto pomnožimo obe strani enačbe. Najboljše pri vsem tem je pa to, da gredo na ta način ulomki pa pa 😉
Linearna enačba ima običajno eno rešitev, ni pa vedno tako. Lahko se tudi zgodi, da enačba nima rešitve ali pa da je rešitev neskončno. Kako vemo, da enačba nima rešitve? Vemo, da kakršno koli množenje z 0 pomeni rezultat 0. Če pri računanju naletimo na zmnožek neznanke in števila 0, katerega rezultat ni enak 0 (na primer x • 0 = 5 ali pa recimo 0 • x = 8), je očitno, da "tu nekaj ne štima". Res je, večkratnik števila 0 mora biti vedno 0, sicer rešitev ne obstaja. Kako pa vemo, da je rešitev neskončno? Že prej smo povedali, da kakršno koli množenje z 0 pomeni rezultat 0. Če pri računanju naletimo na zmnožek neznanke in števila 0, katerega rezultat je enak 0, pa ni nič narobe. Večkratnik števila 0 je vedno 0, ne glede na to, koliko je x oziroma s katerim številom množimo 0. Zato je x lahko katero koli število, torej je rešitev karkoli oziroma ima enačba neskončno rešitev.
Čeprav se čudno sliši, je to povsem običajen postopek pri obračanju enačb, ko želimo izraziti iskano spremenljivko (običajno je to x). Pri tem si velja zapomniti dve glavni pravili: Prvo pravilo: Člen, ki ga ne potrebujemo (to je tisti člen, ki ne vsebuje iskane spremenljivke), preprosto "vržemo" na drugo stran enačbe, ob tem pa mu spremenimo predznak. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Pozitiven člen na levi strani enačaja postane negativen ... ... negativni pa pozitiven: Drugo pravilo: Ko imamo na levi (ali desni) strani enačbe le še tisti člen, ki vsebuje iskano spremenljivko, le-tega "razcepimo", tako da na tej strani enačbe ostane le še iskana spremenljivka, ostale faktorje pa prestavimo na drugo stran enačbe. Ob tem se prestavljenim faktorjem ne spremeni predznak, ampak položaj. Če so bili na eni strani v imenovalcu ulomka, so na drugi strani v števcu in obratno. Oglejmo si še zapis omenjenega postopka z matematičnimi znaki. Faktor, pomnožen s spremenljivko x na levi strani enačaja, se na desni strani preseli v imenovalec ulomka ... ... faktor, ki je na levi strani enačaja v imenovalcu ulomka, pa na desni strani pomnožimo s preostalim delom enačbe: Pozor! Pri drugem pravilu moramo v primeru več členov na desni strani uporabiti oklepaj!
Primer: x/2 = 2a + b x = 2(2a+b) Ste se pri iskanju ničel polinoma kdaj spraševali, zakaj ima ničla vedno nasprotni predznak od predznaka, ki se pojavi v oklepaju razstavljenega polinoma?
Če ste se, je to dober znak, saj želite razumeti, kaj počnete in to je pri matematiki ključnega pomena. Za primer vzemimo polinom: f(x)=x²-x-6 Ko ga razstavimo, dobimo: f(x)=(x-3)(x+2) Ničlo poiščemo tako, da polinom izenačimo z 0: (x-3)(x+2)=0 Da bo zmnožek oklepajev enak 0, mora biti vrednost vsaj enega oklepaja enaka 0, torej:
Če želimo, da bo x-3 enak 0, mora biti vrednost x enaka 3, saj je 3-3 enako 0. K -3 moramo torej postaviti njegovo nasprotno vrednost, da bosta skupaj enaka 0. Na enak način moramo za zagotovitev rezultata x+2=0 k +2 postaviti njeno nasprotno vrednost -2, da bosta skupaj enaka 0. Rešitvi enačbe (in hkrati ničli polinoma) sta torej
Jih znate našteti? ;) Še enkrat jih ponovimo posebej za vas:
Eksplicitna oblika zapisa enačbe premice Najprej razrešimo dilemo med eksplicitnim in implicitnim zapisom. Besedi seveda izvirata iz latinščine, v oči oziroma ušesa pa nas najbolj zbode predpona pri prvi, to je "eks-", ki po latinsko pomeni "izven" oziroma "iz". Kdo je v tem primeru "zunaj"? Odvisna spremenljivka y. Na drugo stran enačaja jo je namreč postavila neodvisna spremenljivka x v družbi koeficientov (številk). To je nekako tako, kot da bi "eks" dekle pred vrata postavilo "eks" fanta. Auč, not good. Na sliki imate primer eksplicitnega zapisa: Implicitna oblika zapisa enačbe premice Če je pri eksplicitnem zapisu odvisna spremenljivka y osamljena, ločena od neodvisne spremenljivke x in številskih koeficientov, je pri implicitnem zapisu le-ta "v dobri družbi". Na drugi strani enačbe pa je ničla, po čemer tak zapis linearne funkcije tudi najlažje prepoznamo. Če še malo "pokukamo" k latinščini, beseda eksplicitno izhaja iz latinskega izraza "implicitus", ki pomeni "vključiti, prepletati" - logično, spet je govora o odvisni spremenljivki y, ki tokrat ni osamljena (juhu :)) Odsekovna oblika zapisa enačbe premice
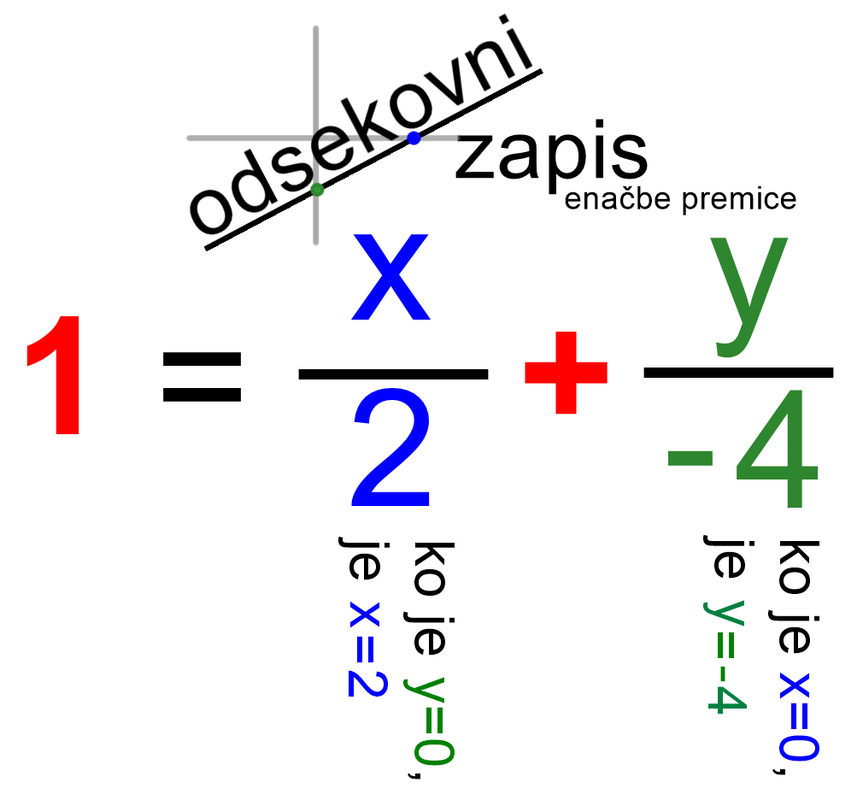
Ta zapis je po eni strani najbolj zakompliciran, po drugi strani pa si ga je najlažje predstavljati, saj je v neposredni povezavi z grafom funkcije. Tokrat je na svoji strani enačbe "osamljena" enica. Kaj nam ta enica pove?
Enkrat je bilo v enem razredu ene šole eno dekle. In rada se je oblačila čisto "po svoje". Ker je bilo njenim sošolkam njeno oblačenje všeč, so jo pri tem posnemale.
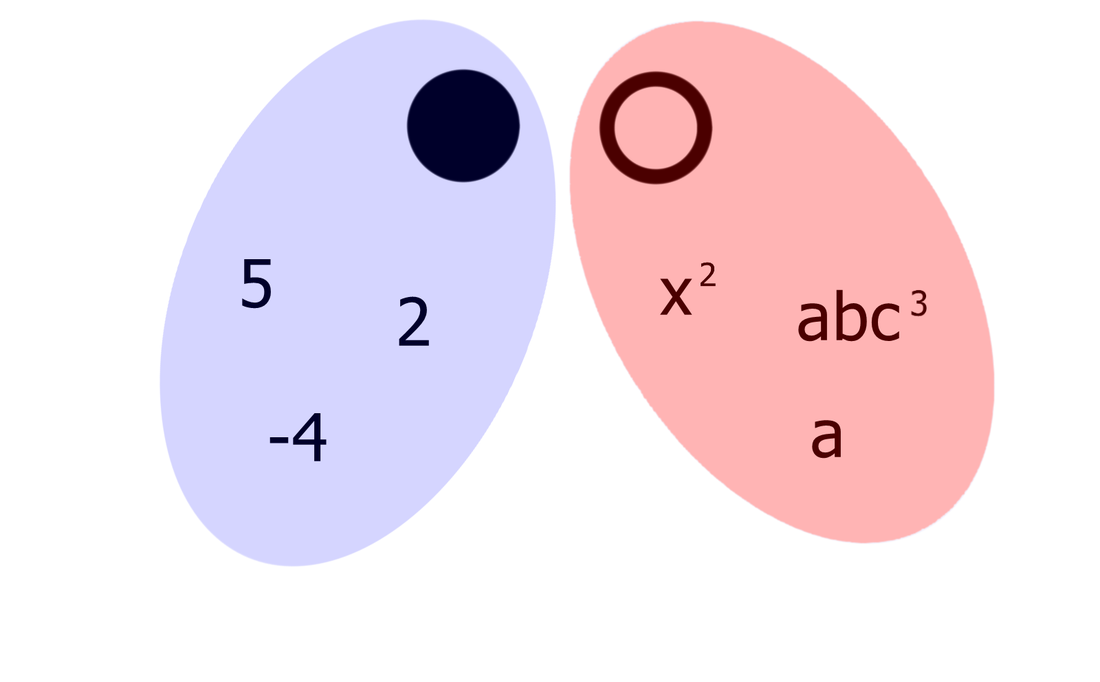
In kje je tu matematika? Dekle, ki se je oblačilo "po svoje", lahko označimo kot neodvisno, medtem ko so posnemovalke od nje odvisne. Resno, kje je tu matematika? Tako kot v zgornji zgodbi imamo tudi pri matematiki spremenljivke, ki so lahko odvisne ali pa neodvisne. Odvisne so seveda odvisne od - neodvisnih :) Odvisno spremenljivko običajno označimo z y, neodvisno pa z x. Na primer: y=2x+4. No, sedaj pa imate matematiko :) Izrazi, enačbe, neenačbe, poenostavljanje, razstavljanje... Nočna mora za tistega, ki ne razume, "šala-mala" za tistega, ki "se mu posveti". Skozi nepregledno množico pravil se bomo tokrat skušali prebiti s pomočjo simbolov, kar bo všeč predvsem tistim, ki ste bolj "vizualni tip". Ponovitev Najprej ponovimo pojem "člen". Poenostavljeno rečeno je člen skupek številk in črk, med katerimi lahko nastopajo še simboli za množenje in deljenje ter eksponenti potenc in koreni. Ne pozabimo: znotraj člena simboli za seštevanje in odštevanje ter predznaka + in - ne nastopajo, razen če niso "ujeti" med oklepaje. So pa s simboli za seštevanje in odštevanje členi povezani med seboj! Definicija simbolov Začnimo z enočlenikom. Označimo ga z dvema krogoma:
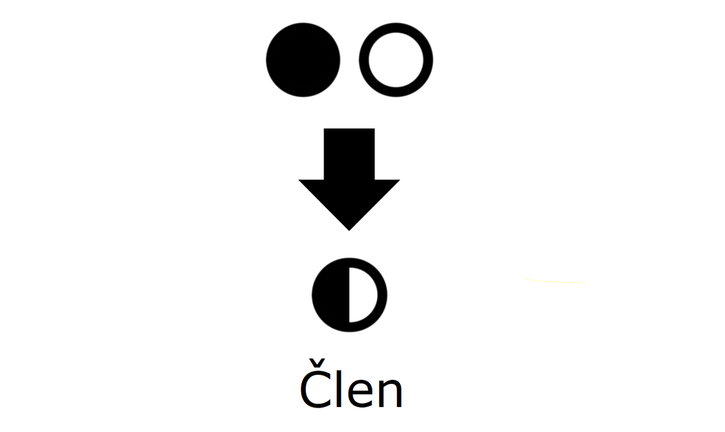
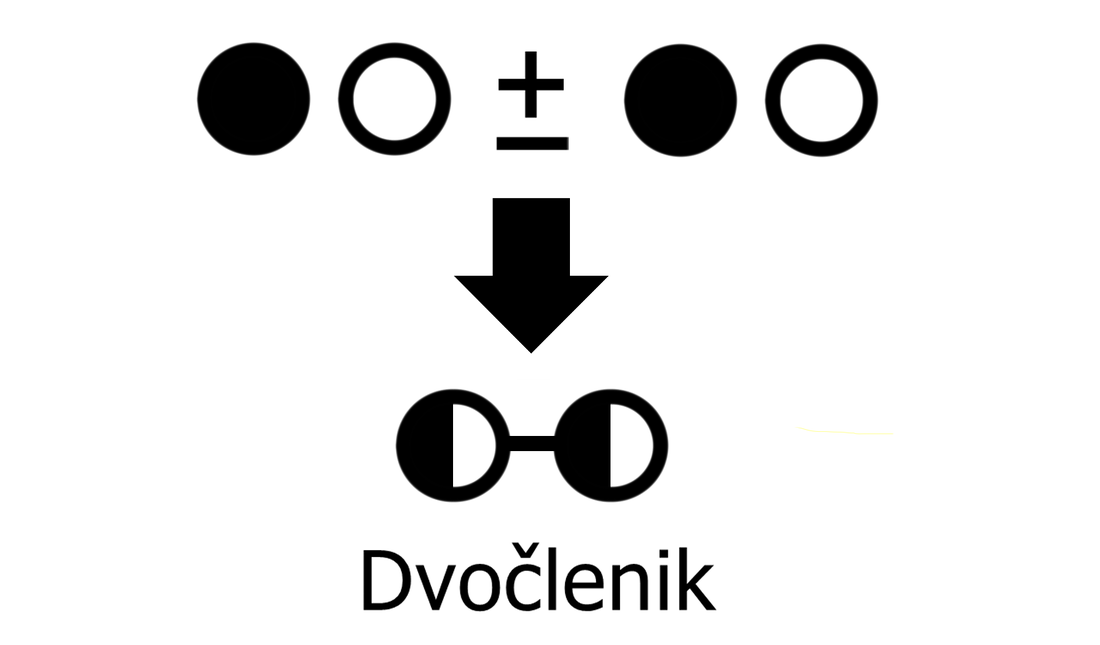
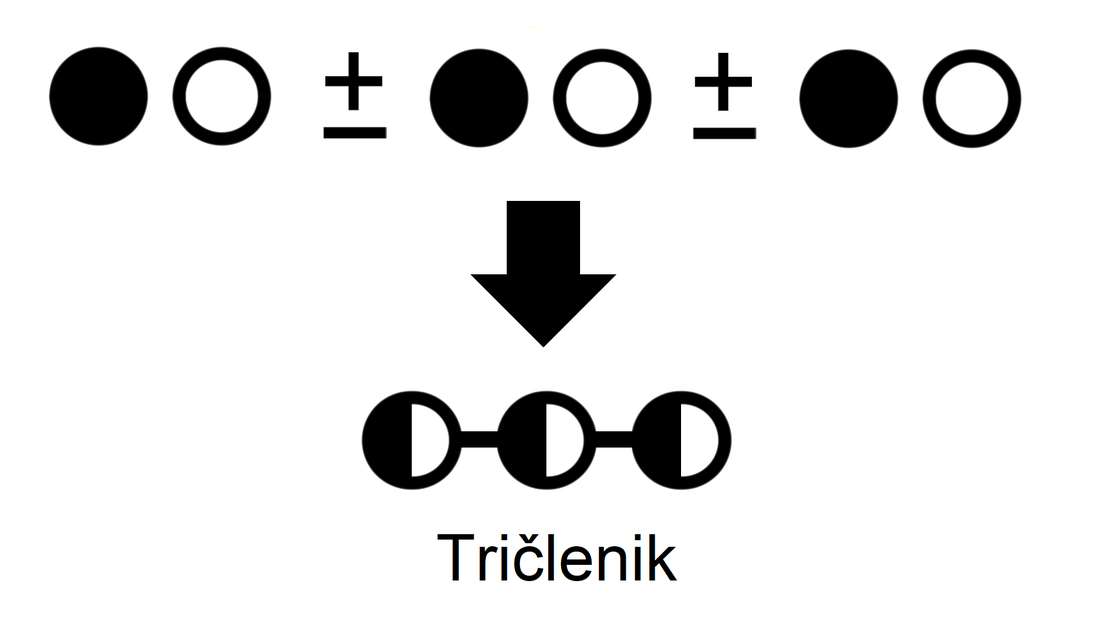
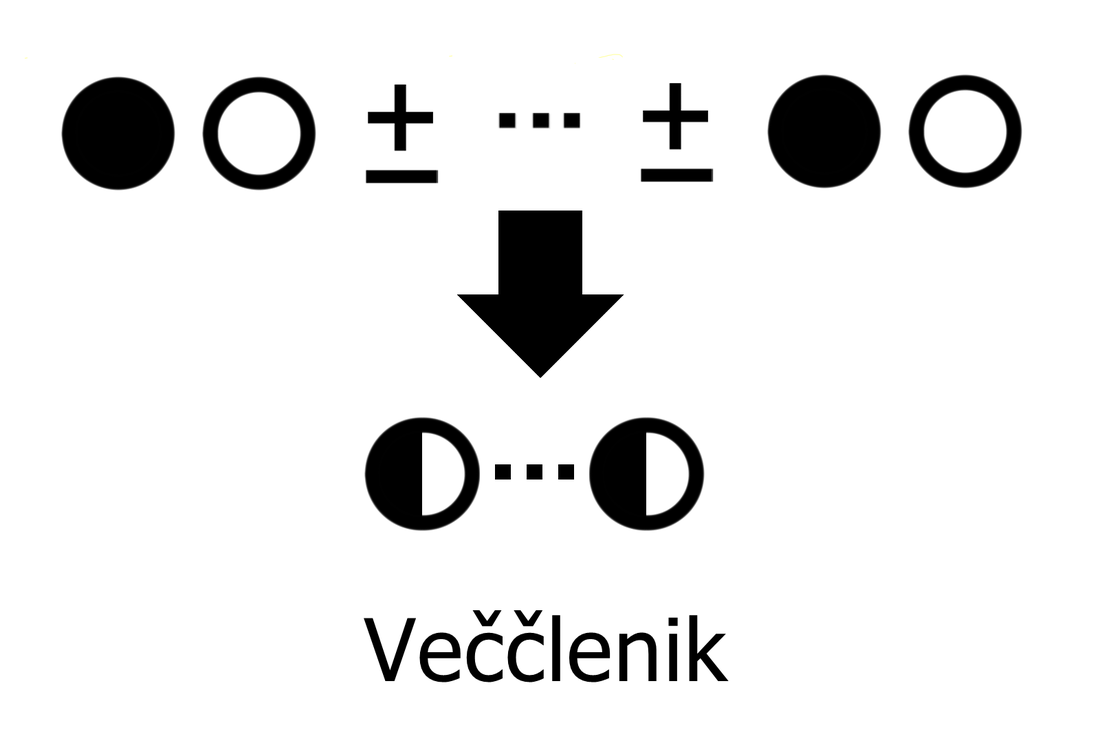
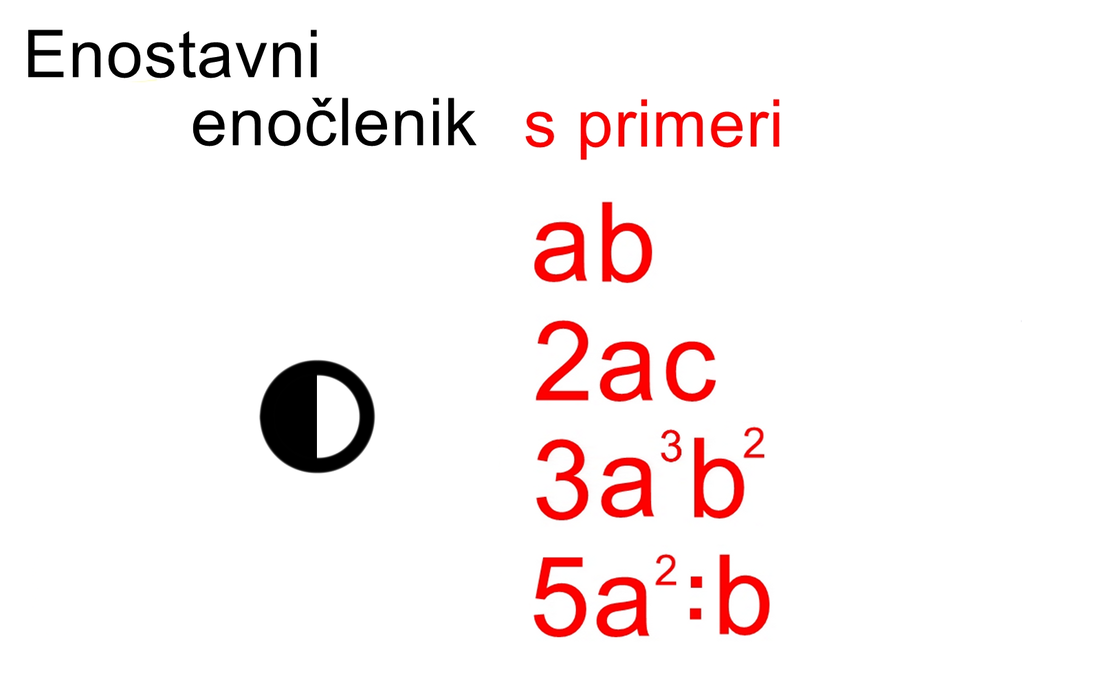
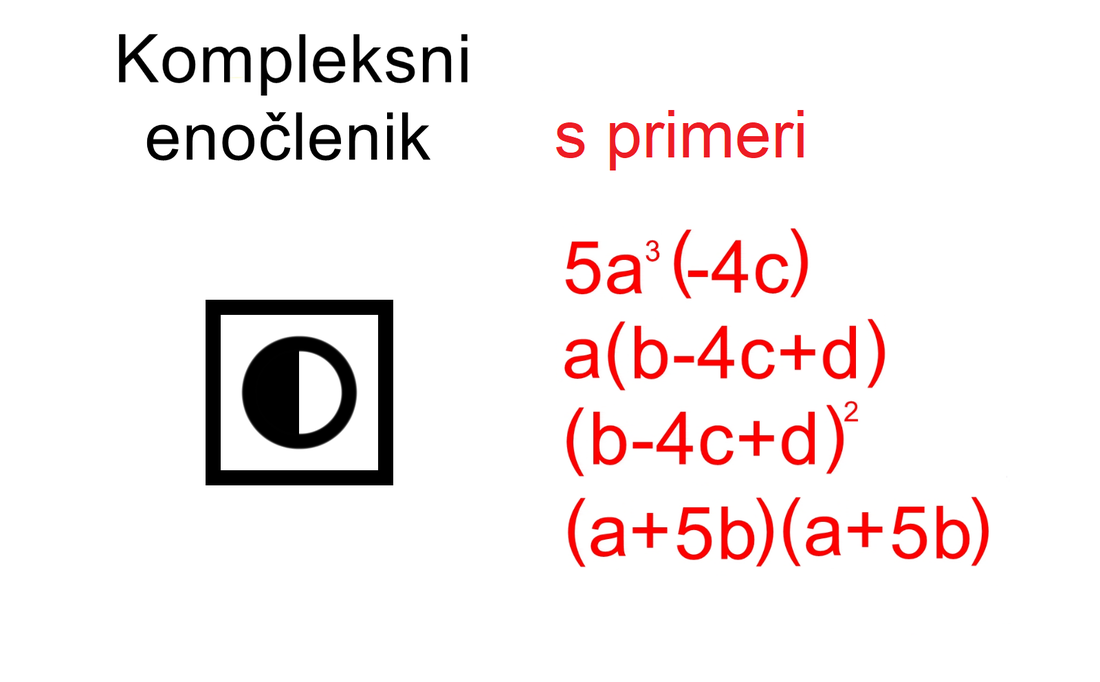
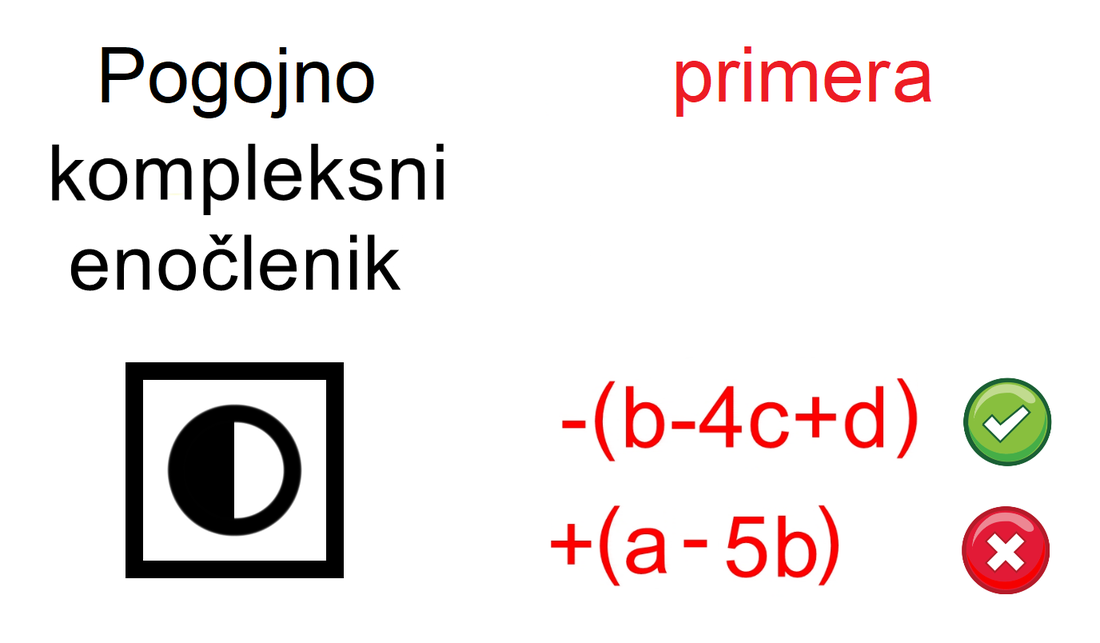
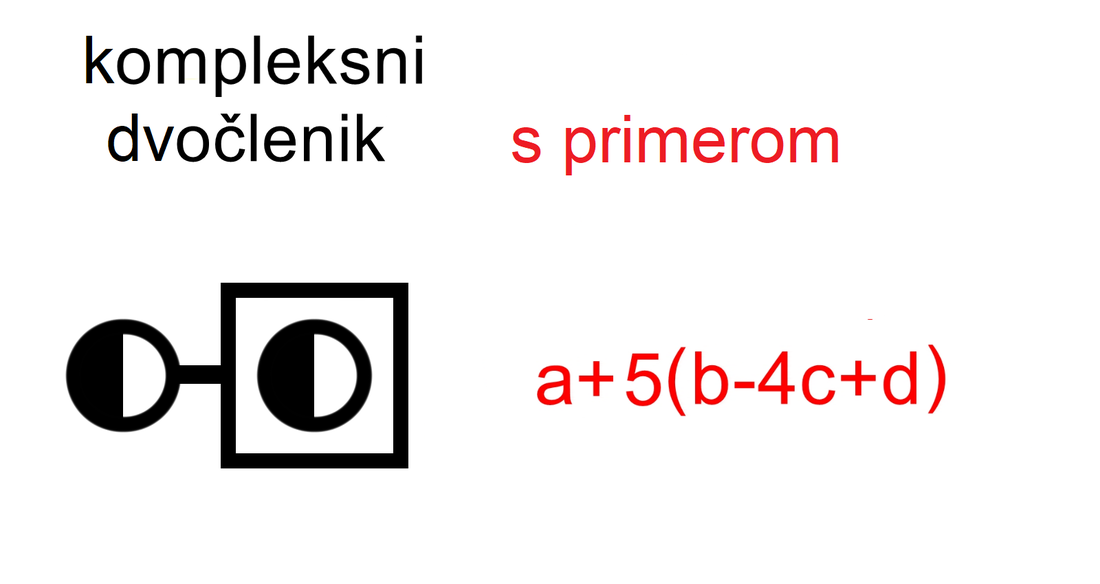
Če enočlenik ne vsebuje spremenljivke (take izraze srečamo v aritmetiki - samo številke, brez črk), rišemo le poln krog. Za boljšo preglednost lahko kombinacijo polnega in praznega kroga poenostavimo: Če med dva člena zapišemo + ali -, dobimo dvočlenik. Mi ga bomo označili takole: V izrazih se pogosto pojavlja tudi tričlenik: Ker je število členov lahko poljubno, dodajmo še simbol za veččlenik: Enočlenika običajno ne predstavljata le koeficient in spremenljivka (številka in črka, na primer 5a), ampak je sestavljen iz več delov, pogosto z oklepaji (na primer a(b-c)(d+e)). Tak enočlenik bomo poimenovali "kompleksni enočlenik". Seznam vseh simbolov je na naslednji sliki: Primeri zapisov s simboli Oglejmo si nekaj primerov za enostavni in kompleksni enočlenik: Če imamo le en oklepaj in pred njim stoji minus, je enočlenik pogojno kompleksni, saj gre v tem primeru za množenje oklepaja s številskim koeficientom -1 (posledično se po odpravi oklepaja vsem členom v oklepaju spremeni predznak): - (b-4c+d) = (-1)·(b-4c+d) = -b+4c-d Če pa pred oklepajem stoji plus, enočlenik ni kompleksen, saj oklepaj v tem primeru sploh ni potreben: + (a-5b) = a-5b Če enostavni in kompleksni enočlenik združimo v dvočlenik, dobimo: Zapis računskih pravil s simboli
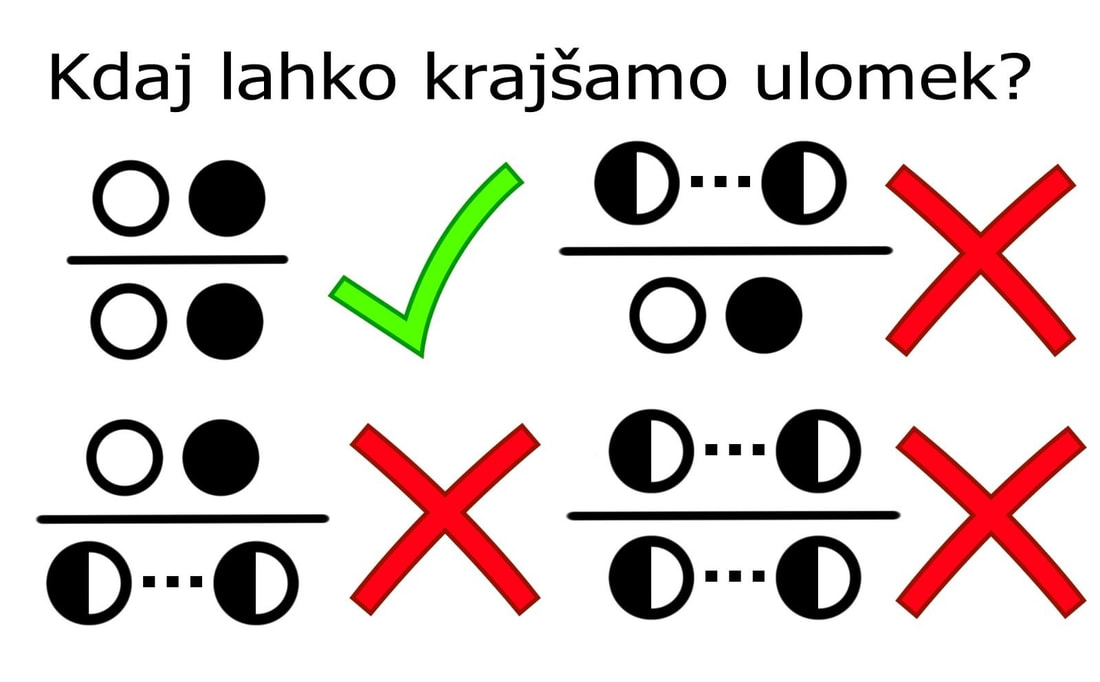
Za primer si oglejmo zapis pravila za krajšanje ulomkov. Ulomek lahko krajšamo samo takrat, kadar je tako v števcu kot v imenovalcu enočlenik. Kadar imamo opravka z veččleniki, jih je potrebno najprej razstaviti: Marsikdo poreče, da učenje matematičnih enačb "na pamet" nima več smisla, odkar je vse na internetu. Res je, vse je na internetu, ampak vaši možgani imajo še vedno krajši dostopni čas od katerekoli hitre internetne povezave;) Šalo na stran, kakšno enačbo je res dobro poznati, predvsem tiste najbolj bistvene, saj vam to lahko močno zniža čas priprav na pisanje domače naloge, tremo na izpitih, olajša organizacijo učenja, pa še kaj bi se našlo. No, in če si enačbo zapomnite na pravi način, ostane res dolgo v glavi;) Začnimo z enačbama za obseg in ploščino kroga. Veste, da si ju je lažje zapomniti "v paru"? Preverite: Še malo legende:
|
ARHIV
May 2024
KATEGORIJE
All
|
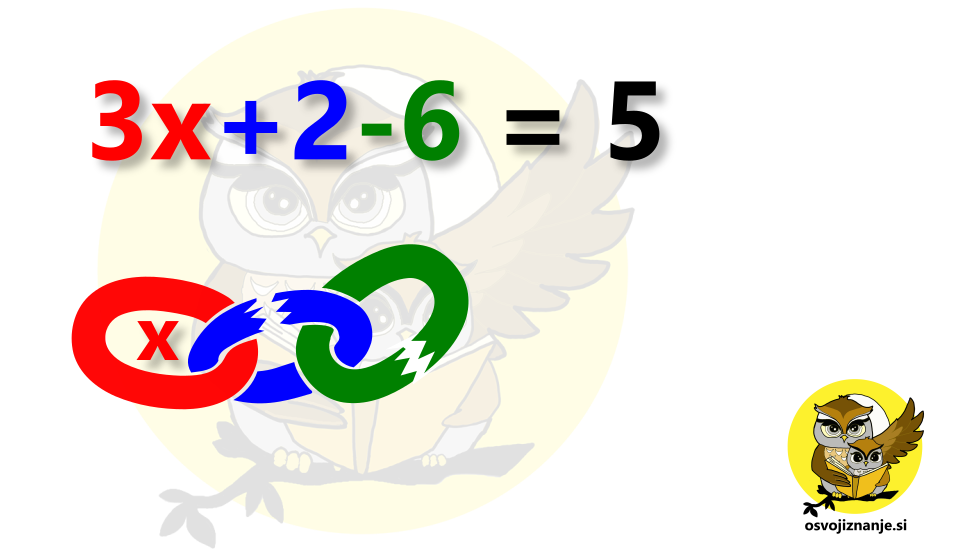
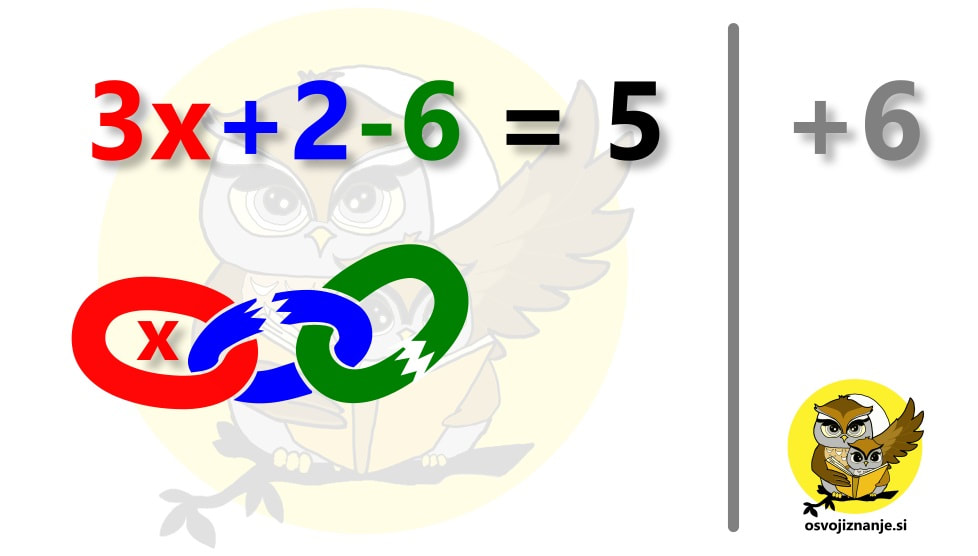

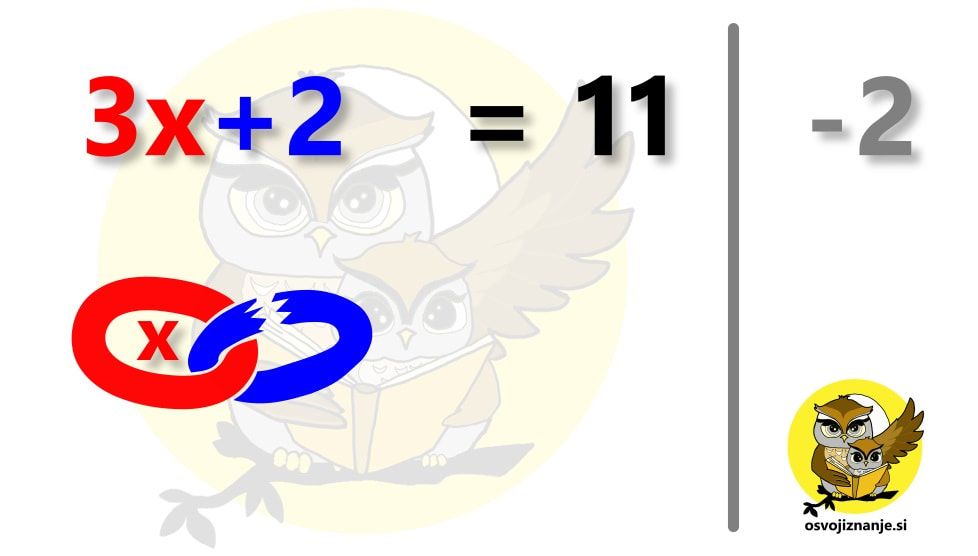






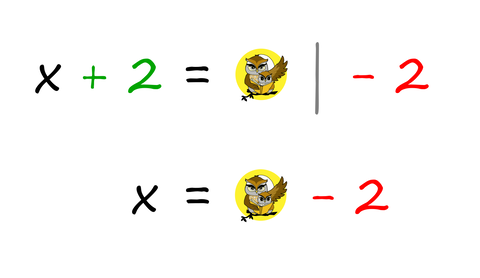
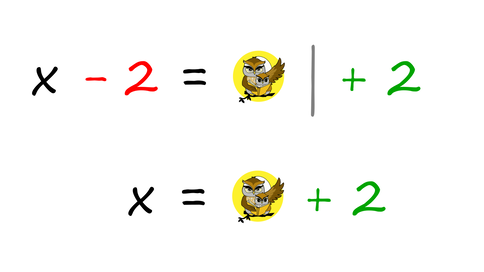
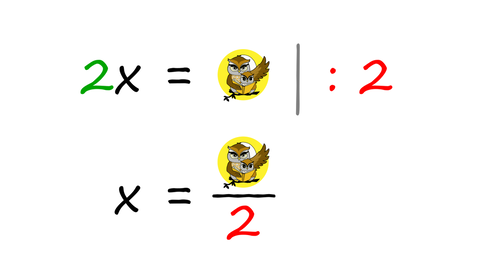
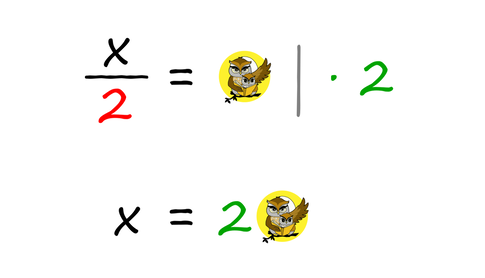
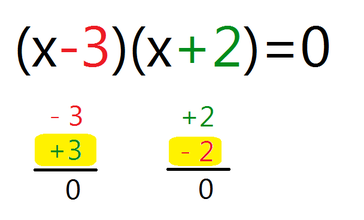




 RSS Feed
RSS Feed
