|
Za tovrstno telovadbo potrebujemo le nekaj znanja poštevanke in...dovolj veliko sobo (če boste delali majhne korake, bo šlo pa tudi v manjši sobi:)).
In kako poteka tale mešanica možganske in mišične telovadbe? Preverimo kar na primeru. Razstavimo izraz x² - 5x -36. Preden se lotimo reševanja, si pripravimo še "teren". Poštevanko verjetno še znamo (če ne, pa hitro malo ponavljat' ;) ), v sobi moramo pa označiti "točko nič", ki bo predstavljala število 0. V eno smer od te točke bodo koraki naprej oziroma "v plus", v drugo pa koraki nazaj oziroma "v minus". Začnimo s številom 36. Pomislimo na vse rezultate poštevanke, ki znašajo 36. Naloga je nekoliko zahtevnejša od "klasične", saj jo opravljamo v obratni smeri. 36 vemo, da je enako:
Dobili smo pet kombinacij množenca in množitelja. Vsak tak par (na primer 3 in 12, 4 in 9,...) nam predstavlja število korakov. Naša naloga je, da ugotovimo, s katerim parom korakov lahko pridemo do koeficienta linearnega člena. V našem primeru je to -5, torej moramo biti na koncu sprehoda 5 korakov "v minusu". Začnemo pa vedno na "točki nič". Pri tej nalogi je pomembno tudi to, kakšen je predznak pri številskem členu:
V našem primeru je številski člen negativen (-36), zato bomo korake delali "mal' naprej in mal' nazaj" (ali pa obratno, po želji :)) Po kombinaciji možganske in mišične telovadbe ugotovimo, da do 5 korakov "v minus" pridemo lahko tako, da naredimo 4 korake naprej in 9 korakov nazaj (lahko tudi najprej 9 korakov nazaj in nato 4 korake naprej). Za rešitev smo uporabili torej četrti par števil (oziroma korakov) iz zgornjega seznama, 4 in 9. Rešitev se torej glasi: x² - 5x -36 = (x+4)(x-9) saj smo do cilja prišli tako, da smo naredili 4 korake naprej in 9 korakov nazaj.
0 Comments
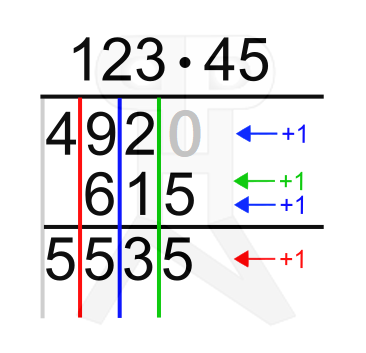
V šoli že leta učijo vedno eno in isto metodo za množenje. Največji argument za to je nevarnost, da bi se učenci ob različnih metodah preveč zbegali in potem vse pomešali. Delno je to res, saj se v šoli ponavadi učimo postopkov in dva postopka za isto stvar bi nas res lahko zmedla. Po drugi strani pa se določeno snov lahko bolje naučimo, če jo pogledamo iz več zornih kotov. Ne nazadnje se tudi pri vsakem nakupu (npr. mobilnega telefona), kjer imamo "v igri več favoritov", o vsakem izmed njih poučimo mnogo bolje, kot pa da bi kupili prvi telefon, ki nam "pride pod roke". Zato smo vam pripravili primerjavo treh najbolj uporabljanih metod za množenje dveh večmestnih števil ter navedli njihove glavne prednosti in slabosti. Prvo metodo smo poimenovali "klasična", to verjetno vsi poznamo iz šole. Druga je "metoda z mrežo", ki je aktualna predvsem na angleško govorečem področju (zanimiva za tiste, ki radi naročate knjige iz tujine). Tretja metoda pa je "japonska" in bo všeč predvsem tistim, ki radi rišete. Vse tri metode bodo predstavljene skozi primer množenja števil 123 in 45. Klasična metoda Postopek:
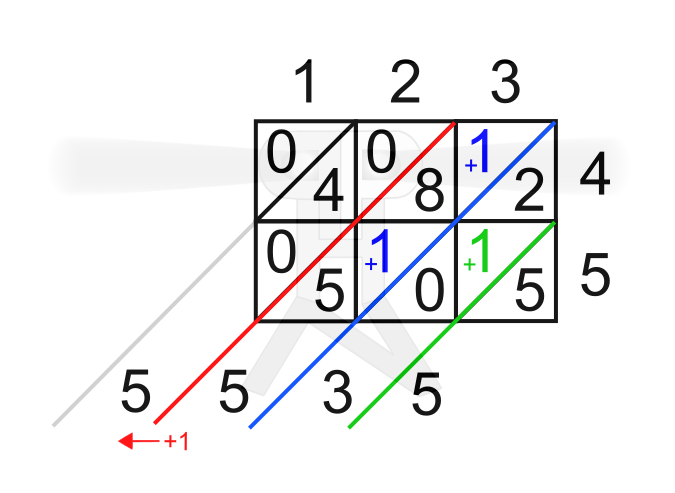
Prenos naprej: Prvič (po potrebi) prenašamo vrednost desetice naprej oz. levo pri množenju (v našem primeru je npr. pri množenju števk 3 in 4 rezultat 12, kjer zapišemo enico (2), desetico (1) pa prenesemo naprej), nato pa (po potrebi) še pri seštevanju zmnožkov (v našem primeru je npr. pri seštevanju 9 in 6 rezultat 15, kjer zapišemo enico (5), desetico (1) pa prenesemo naprej). Prednosti: Zasede najmanj prostora, večja preglednost. Slabosti: Množenje večmestnega števila z enomestnim (pri metodi z mrežo in japonskem načinu vedno množimo samo enomestna števila), nepregledno zapisovanje prenosa naprej (pri metodi z mrežo sta "moder" in "zelen" prenos naprej zapisana na točno določenem mestu v tabeli, pri klasičnem pa običajno med velike cifre vrivamo majhne enice, ki nas spomnijo, da moramo narediti prenos naprej). Metoda z mrežo Postopek:
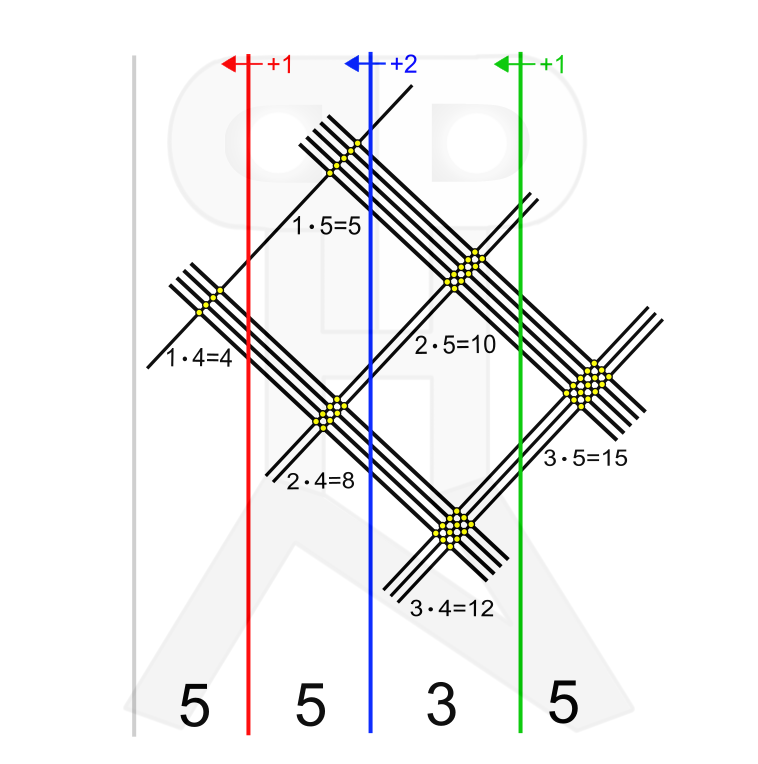
Prenos naprej: Prenos naprej pri množenju ni potreben, po potrebi vrednost desetice prenesemo naprej pri seštevanju zmnožkov. V našem primeru je npr. pri seštevanju 5, 1, 8 in 1 rezultat 15, kjer zapišemo enico (5), desetico (1) pa prenesemo naprej. Prednosti: Prenos naprej pri množenju ni potreben. Slabosti: Potrebno je dorisati prečne črte med enicami/deseticami/stoticami/..., potrebno je paziti, da števila pravilno vnesemo v tabelo (od leve proti desni in od zgoraj navzdol). Japonska metoda Postopek:
Prenos naprej: Prenos naprej se izvaja samo v končnem koraku, ko seštevek točk v posameznem "stolpcu" zapisujemo na dno "stolpca". V našem primeru je npr. pri seštevanju 2•5=10, 3•4=12 in prenešene 1 rezultat 23, kjer zapišemo enico (3), desetico (2) pa prenesemo naprej. Prednosti: Vizualna metoda, motivacija za učenje poštevanke (z znanjem poštevanke lahko hitreje računamo). Slabosti: Potrebno je pravilno narisati črte (tako tiste za števke kot ločne črte med enicami/deseticami/stoticami...), zasede veliko prostora, dolgotrajno štetje točk (če ne znamo poštevanke). Opisali smo tri metode, nedvomno pa jih obstaja še več. Zanimiv način množenja dveh večmestnih števil je tudi uporaba zakona o distributivnosti množenja, o katerem si lahko več preberete tule. Množenje z distributivnostnim zakonom je uporabno za števila, ki se na številski osi nahajajo blizu "okroglih" vrednosti, na primer 98 in 103, ki sta blizu vrednosti 100: 98•103 = (100-2)(100+3) = 10000 + 300 - 200 - 6 = 10094 Odgovor je popolnoma preprost: Najmanjši skupni večkratnik (v) si lahko predstavljamo je najnižjo točko stalaktita (ta visi s stropa jame), največji skupni delitelj (D) pa kot najvišjo točko stalagmita (ta pa raste s tal navzgor). Zakaj? Zato, ker je najmanjši skupni večkratnik (kljub temu, da je najmanjši) še vedno večji od največjega skupnega delitelja. Je pa še vedno najmanjši skupni večkratnik manjši od ostalih skupnih večkratnikov, največji skupni delitelj pa večji od ostalih skupnih deliteljev. To se lepo vidi na sliki s primerom: Ob primeru pa še nekaj nasvetov:
|
ARHIV
May 2024
KATEGORIJE
All
|
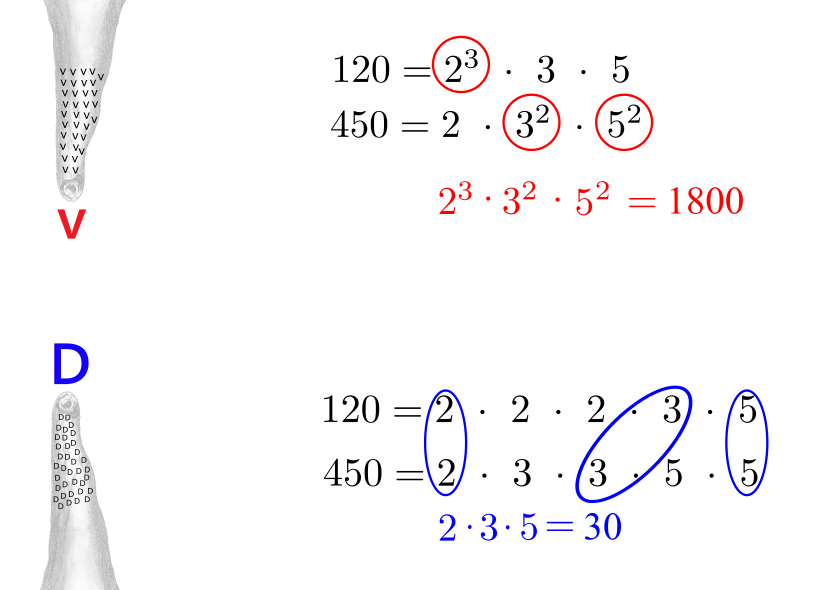
 RSS Feed
RSS Feed
