|
Odgovor je popolnoma preprost: Najmanjši skupni večkratnik (v) si lahko predstavljamo je najnižjo točko stalaktita (ta visi s stropa jame), največji skupni delitelj (D) pa kot najvišjo točko stalagmita (ta pa raste s tal navzgor). Zakaj? Zato, ker je najmanjši skupni večkratnik (kljub temu, da je najmanjši) še vedno večji od največjega skupnega delitelja. Je pa še vedno najmanjši skupni večkratnik manjši od ostalih skupnih večkratnikov, največji skupni delitelj pa večji od ostalih skupnih deliteljev. To se lepo vidi na sliki s primerom: Ob primeru pa še nekaj nasvetov:
0 Comments
Leave a Reply. |
ARHIV
December 2023
KATEGORIJE
All
|
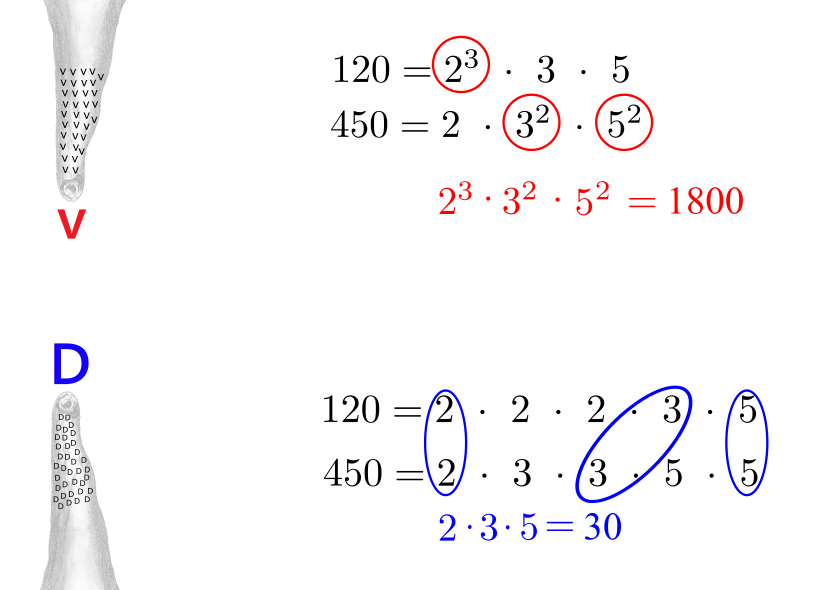
 RSS Feed
RSS Feed
