Kaj so to številska drevesa? Po domače povedano so to drevesa, na katerih namesto jabolk rastejo števila, obrnjena pa so z glavo navzdol. Vam je zdaj kaj bolj jasno? Manj? :) 

Pravijo, da slika pove več kot 1000 besed, zato si poglejmo primer.

Razdelimo število 123 na desetiške enote in ga zapišimo v obliki:

Predstavitev števila na tak način nam olajša računanje "na plus in minus", recimo:

• seštevanje brez prehoda,
• seštevanje s prehodom,
• odštevanje brez prehoda,
• odštevanje s prehodom.

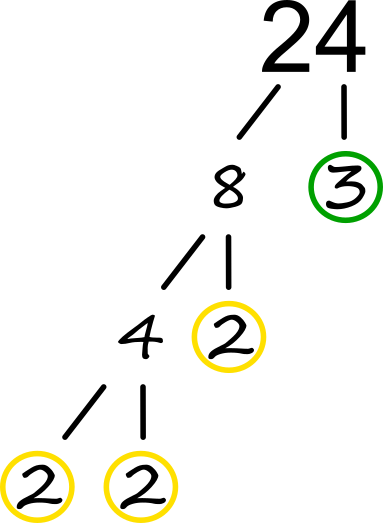
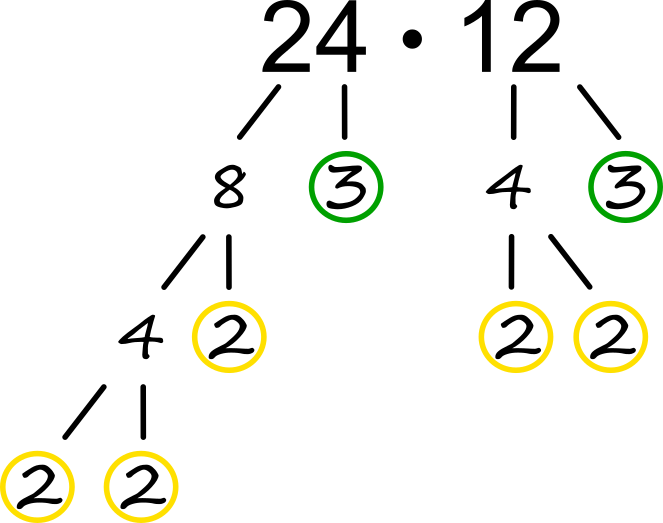
Število lahko zapišemo tudi v obliki prafaktorjev. Pri nas razcep števila na prafaktorje v šolah običajno učijo na način z navpično črto (nekajkrat smo ga uporabili tudi v naših video vsebinah), v tujini pa se ga lotijo tudi takole (angl. izraz "factor tree"):

Razcep izvajamo s postopnim "drobljenjem" števila, na podlagi poznavanja poštevanke.

​Za 24 vemo, da je 8 krat 3. 3 je že praštevilo, zato se tu veja konča, 8 pa delimo naprej, vse dokler ne pridemo še do preostalih prafaktorjev.

Drevo bi lahko npr. začeli tudi s "6 krat 4"; v tem primeru bi bila struktura drevesa drugačna, na koncu pa bi dobili iste prafaktorje kot na zgornji sliki.

Predstavitev števila na tak način nam olajša računanje "na krat in deljeno" ter še kar nekaj drugih računskih operacij, ki iz omenjenega izhajajo, recimo:

• množenje,
• deljenje (brez ostanka),
• izpostavljanje skupnega večkratnika,
• krajšanje ulomkov,
• potenciranje,
• (delno) korenjenje.

S pomočjo praštevilske faktorizacije si močno poenostavimo tudi iskanje najmanjšega skupnega večkratnika, največjega skupnega delitelja ter najmanjšega skupnega imenovalca ulomkov.

Če združimo tako zapis v obliki desetiških enot kot razcep na prafaktorje, pa si lahko pomagamo tudi pri računskih izrazih in deljenju z ostankom.

Za boljšo preglednost in ločevanje vrst dreves se dogovorimo še za označevanje:

• desetiške enote naj bodo v okvirčkih,
• prafaktorji pa v krožcih.

Tako okvirčki kot krožci naj bodo ločeni po barvah.

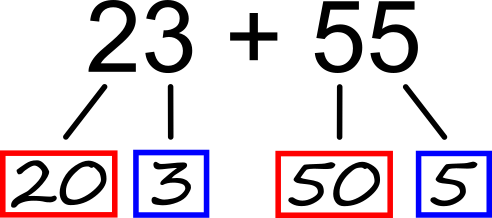
Omenjeno znanje nam pomaga tudi pri računanju na pamet, ki je ob hitrem preverjanju pravilnosti rezultatov na koncu pisnih testov praktično nepogrešljivo.

Oglejmo si nekaj primerov tovrstnega računanja.

Seštevanje brez prehoda
​

Na podlagi drevesnega zapisa hitro ugotovimo:

• 20 + 50 = 70 in
• 3 + 5 = 8

Ko to dvoje seštejemo, dobimo rezultat 78.

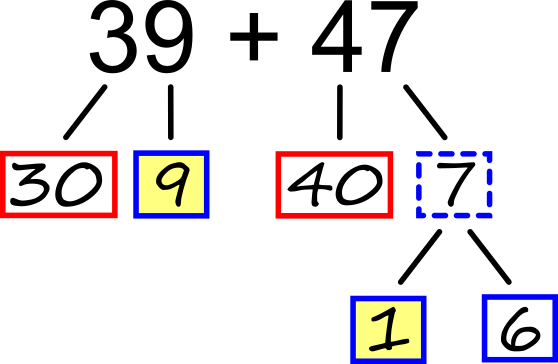
Seštevanje s prehodom
​

Desetice enostavno seštejemo:

• 30 + 40 = 70

Ko pa seštejemo enice, ugotovimo, da imamo prehod čez desetico:

• 9 + 7 = 16

Zato enico drugega seštevanca (7) razdelimo še naprej in sicer tako, da del le-te z enico prvega seštevanca (9) tvori točno desetico (obarvano rumeno):

• 9 + 1 = 10

Od enice drugega seštevanca (7) nam torej ostane še 6, ki pa jo bomo prišteli čisto na koncu:

• 30 + 40 = 70
• 9 + 1 = 10
• 6 ostane od enice drugega seštevanca

Ko vse skupaj seštejemo, dobimo rezultat 86.

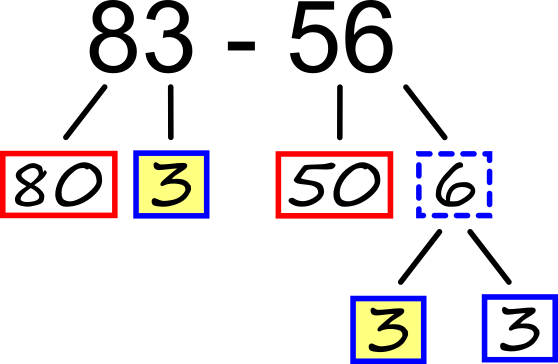
V našem primeru smo si ogledali prehod čez desetico. Na podoben način bi si lahko pomagali tudi pri prehodu čez stotico, tisočico ...

Odštevanje brez prehoda

Na podlagi drevesnega zapisa hitro ugotovimo:

• 70 - 40 = 30 in
• 8 - 3 = 5

Ko to dvoje seštejemo, dobimo rezultat 35. Prav se prebrali, seštejemo :) Desetice in enice smo seveda ločeno odšteli, a na koncu število vedno "zložimo" tako, da vrednosti, ki jih prispevajo posamezne desetiške enote (v našem primeru desetice in enice) seštejemo:

• 30 + 5 = 35

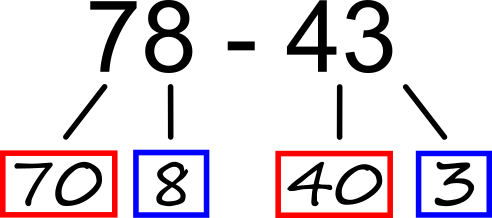
Odštevanje s prehodom
​

Če ne bi imeli prehoda, bi preprosto odšteli desetice in enice, tako kot v prejšnjem primeru. A Ker računa "3 - 6" v okviru naravnih števil ne moremo izračunati, smo enico odštevanca (6) razdelili še naprej in sicer tako, da se del le-te ujema z enico zmanjševanca (3, obarvano rumeno).

Račun nato izračunamo postopoma:

• 80 - 50 = 30
• 3 - 3 = 0 (obarvano rumeno); ta del lahko sedaj "pozabimo", saj na končni izračun ne vpliva (če številu prištejemo ali odštejemo 0, se ne zgodi nič)
• ​Od števil v okvirčkih nam je ostala samo še (neobarvana) 3 pri odštevancu, ki jo odštejemo od 30

Rezultat je torej 27.

Dodatek: Če nalogo razširimo na cela števila, si lahko pomagamo s "trikom", ki je razložen tule.

Množenje

Če oba faktorja razcepimo na prafaktorje, rezultat lahko preprosto zapišemo v obliki potenc:

• 2∙2∙2∙2∙2 = 2⁵
• 3∙3 = 3²

Ko to dvoje zmnožimo, dobimo rezultat 2⁵∙3²

Rezultat lahko razmeroma hitro dobimo tudi z množenjem praštevil, kjer upoštevamo:

• vrstni red od večjih praštevil  proti manjšim (z vsakim množenjem je delni rezultat večje število, zato je bolje, da manjša praštevila pustimo za na konec)
• zmnožek praštevil 2 in 5 je 10, zato take pare z delnim rezultatom množimo skupaj (nov delni rezultat dobimo le z dodajanjem ničle na desno)

V našem primeru bi tako izračunali:

• 3∙3 = 9

• 9∙2 = 18
• 18∙2 = 36
• 36∙2 = 72
• 72∙2 = 144
• 144∙2 = 288

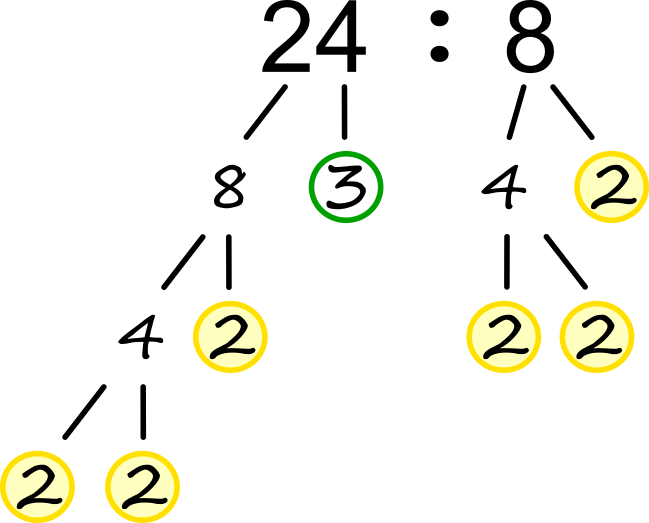
Do rezultata seveda lahko pridemo tudi s pisnim množenjem, kjer pa si s številskimi drevesi lahko pomagamo le v manjši meri.

Deljenje

Tako kot smo pri odštevanju ločeno odšteli desetice in enice, lahko pri deljenju enako storimo s prafaktorji, ki smo jih dobili s praštevilskim razcepom deljenca (24) in delitelja (8), saj je koncept odštevanja in deljenja zelo podoben.

Račun izračunamo postopoma:

• 2 (z leve, zapolnjen krog) : 2 (z desne, zapolnjen krog) = 1 (ponovimo 3-krat, nato pa ta del lahko "pozabimo", saj na končni izračun ne vpliva (če število množimo ali delimo z 1, se ne zgodi nič)
• na levi strani nam tako ostane le še 3, ki jo delimo z 1∙1∙1 (=1), ki je po trikratnem deljenju z 2 ostala na desni

Rezultat je torej 3.

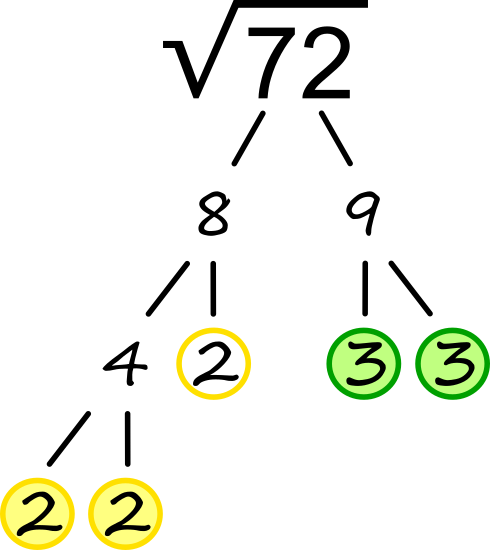
Za razmislek: Ob upoštevanju, da je deljenje je isto kot krajšanje ulomkov, s pomočjo številskih dreves skušaj okrajšati ulomek 24/8.

Delno korenjenje

Če število pod korenom razcepimo na prafaktorje, ga lahko zapišemo v obliki potenc:

• 72 = 2∙2∙2∙3∙3 
  

Ker vemo, da je kvadratni koren kvadrata števila enak številu samemu (√a²=a), ob upoštevanju pravil za korenjenje kvadrate števil lahko "vzamemo izpod korena". Pred tem moramo prafaktorje le še ustrezno grupirati:

• 2∙2∙2∙3∙3 = 2²∙2∙3²

Grupirani prafaktorji so označeni z zapolnjenimi krožci.

Končni rezultat je torej: √72 = √2²∙2∙3² = 2∙3√2

Pod korenom je ostal prafaktor 2, ker "nima svojega para".

20 + ☐ - 10 = 40

Saj poznate tale tip naloge, kajne? :)

Kako najlažje ugotoviti, kaj je potrebno vpisati v okvirček?

Enačaj nam pri tem lahko močno pomaga. Kaj pomeni "je enako"? Dobesedno pomeni "je enako" :) In kaj je enako? Seštevek števil na levi in na desni. No, na desni nam niti računati ni potrebno, ker imamo le eno število :)

Opomba: govora je o seštevku, števil na levi strani. Zraven seveda štejemo tudi odštevanje, ki je v bistvu prištevanje nasprotnih števil.

Računali bomo torej le na levi strani. Zapišimo levo stran računa še "v barvah", da bo lažje razumljiv:

20 + ☐ - 10 = 40

Pri "barvanju" smo upoštevali, da znak za računsko operacijo vpliva na število, ki mu sledi (na desni) in ne na število pred njim oziroma (na levi). Več o tem si lahko preberete tule.

Ljudje smo (večinoma) narejeni tako, da se najprej lotimo tistega, kar poznamo, šele nato pa neznanega. Tudi tu bomo naredili tako. Komur okvirček ni všeč, račun lahko zapiše tudi takole:

20 + ? - 10 = 40

"Naberimo" torej na levi strani skupaj tisto, kar poznamo ...

20 - 10 

... in izračunajmo:

20 - 10 = 10

Kaj nam je torej do sedaj uspelo narediti? Na levi strani smo združili znano in dobili:

10 + ☐ = 40

Tole je pa že kanček lažje, kajne? :) Zopet se spomnimo na enačaj, ki nam pove, da mora biti rezultat na levi strani enak rezultatu na desni.

Če imamo na levi strani 10, na desni pa 40, nam na levi nekaj manjka. Koliko moramo torej dodati na levi strani, da dobimo isto, kot imamo na desni? Odgovor je 30, saj velja

10 + 30 = 40

Opomba: Sklepali bi lahko tudi, da imamo na desni strani 30 preveč, kar je sicer pravilno, a potem računa ne bi mogli rešiti, saj se okvirček nahaja na levi in ne na desni strani.

V okvirček tako zapišemo 30 in celoten račun se glasi:

20 + 30 - 10 = 40

Če naredimo preizkus, na levi strani res dobimo 40.

Še nasvet za konec: Namesto (abstraktnih) števil lahko pri enačenju uporabimo tudi konkretne pripomočke - štejemo kocke, kroglice, denar ... ali pa tehtamo.

Deljenje. Za nekoga "u izi, navadn", za drugega nočna mora.

Najlažje je, če si ga predstavljamo "v živo". Ko ga enkrat dojamemo, je res povsem "simpl" :)

Prva težava se ponavadi pojavi že pri samih izrazih. Zakaj neki​ deljenec, delitelj in količnik? Imajo mogoče koliščarji kaj tu zraven??

Vam je zdaj kaj bolj jasno? Vidite, da koliščarjev res ni bilo zraven :)

Ostanimo še nekoliko pri enakih delih. Veste, da si z deljenjem lahko pomagamo pri delitvi pravokotnika na enake dele? Če smo povsem iskreni, gredo tu zasluge bolj množenju, obratni operaciji deljenja. Aja, pa ulomek je isto kot deljenje, če ste slučajno pozabili ;)

Za lažjo predstavo si oglejte še našo igro "Matematični osvajalci".

No, pa razložimo tole zgodbico lepo in počasi :)

Enkrat je bila ena premica. Ime je dobila po tem, ker je bila revica vsa prema (po SSKJ: prema = ravna). Bila je svobodna. Segala je v eno in drugo smer v neskončnost.

Potem pa je prišla od neznano kje ena točka in se je usedla nanjo, tako grdo, da jo je kar razpolovila. Na njenem mestu sta nastala dva poltraka, a nobeden od njiju ni bil povsem svoboden. V neskončnost sta se raztezala le v eno smer, medtem ko ju je na drugi strani omejevala - kdo drug kot grozna točka.

Naša premica je pa imela sorodnico, ki se ji je pripetila nekoliko drugačna prigoda. Točke so imele prvenstvo v padalskih skokih. Med tekmovalkami sta bili tudi točka A in točka B. Sicer sta želeli pristati na isto mesto, a jima ni uspelo, tako da je bila med njima kar precejšnja razdalja. Omenjeno situacijo je slikal fotograf, ki je bil slučajno matematik in je sklenil, da bo del premice med točkama A in B poimenoval kar daljica. In še danes je tako.

Linearna enačba ima običajno eno rešitev, ni pa vedno tako.

Lahko se tudi zgodi, da enačba nima rešitve ali pa da je rešitev neskončno.

Kako vemo, da enačba nima rešitve? Vemo, da kakršno koli množenje z 0 pomeni rezultat 0. Če pri računanju naletimo na zmnožek neznanke in števila 0, katerega rezultat ni enak 0 (na primer x • 0 = 5 ali pa recimo  0 • x = 8), je očitno, da "tu nekaj ne štima". Res je, večkratnik števila 0 mora biti vedno 0, sicer rešitev ne obstaja.