Računanje z naravnimi števili s pomočjo številskih dreves

Kaj so to številska drevesa? Po domače povedano so to drevesa, na katerih namesto jabolk rastejo števila, obrnjena pa so z glavo navzdol. Vam je zdaj kaj bolj jasno? Manj? :) 

Pravijo, da slika pove več kot 1000 besed, zato si poglejmo primer.

Razdelimo število 123 na desetiške enote in ga zapišimo v obliki:

Predstavitev števila na tak način nam olajša računanje "na plus in minus", recimo:

• seštevanje brez prehoda,
• seštevanje s prehodom,
• odštevanje brez prehoda,
• odštevanje s prehodom.

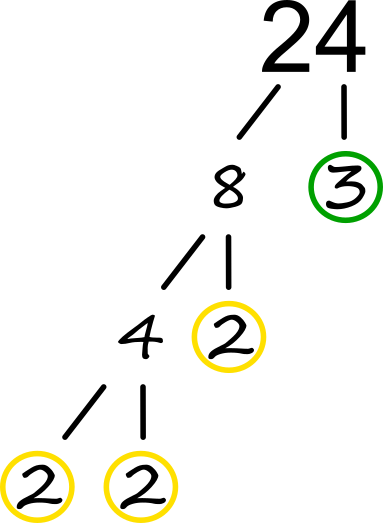
Število lahko zapišemo tudi v obliki prafaktorjev. Pri nas razcep števila na prafaktorje v šolah običajno učijo na način z navpično črto (nekajkrat smo ga uporabili tudi v naših video vsebinah), v tujini pa se ga lotijo tudi takole (angl. izraz "factor tree"):

Razcep izvajamo s postopnim "drobljenjem" števila, na podlagi poznavanja poštevanke.

​Za 24 vemo, da je 8 krat 3. 3 je že praštevilo, zato se tu veja konča, 8 pa delimo naprej, vse dokler ne pridemo še do preostalih prafaktorjev.

Drevo bi lahko npr. začeli tudi s "6 krat 4"; v tem primeru bi bila struktura drevesa drugačna, na koncu pa bi dobili iste prafaktorje kot na zgornji sliki.

Predstavitev števila na tak način nam olajša računanje "na krat in deljeno" ter še kar nekaj drugih računskih operacij, ki iz omenjenega izhajajo, recimo:

• množenje,
• deljenje (brez ostanka),
• izpostavljanje skupnega večkratnika,
• krajšanje ulomkov,
• potenciranje,
• (delno) korenjenje.

S pomočjo praštevilske faktorizacije si močno poenostavimo tudi iskanje najmanjšega skupnega večkratnika, največjega skupnega delitelja ter najmanjšega skupnega imenovalca ulomkov.

Če združimo tako zapis v obliki desetiških enot kot razcep na prafaktorje, pa si lahko pomagamo tudi pri računskih izrazih in deljenju z ostankom.

Za boljšo preglednost in ločevanje vrst dreves se dogovorimo še za označevanje:

• desetiške enote naj bodo v okvirčkih,
• prafaktorji pa v krožcih.

Tako okvirčki kot krožci naj bodo ločeni po barvah.

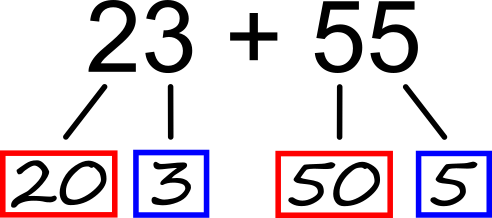
Omenjeno znanje nam pomaga tudi pri računanju na pamet, ki je ob hitrem preverjanju pravilnosti rezultatov na koncu pisnih testov praktično nepogrešljivo.

Oglejmo si nekaj primerov tovrstnega računanja.

Seštevanje brez prehoda
​

Na podlagi drevesnega zapisa hitro ugotovimo:

• 20 + 50 = 70 in
• 3 + 5 = 8

Ko to dvoje seštejemo, dobimo rezultat 78.

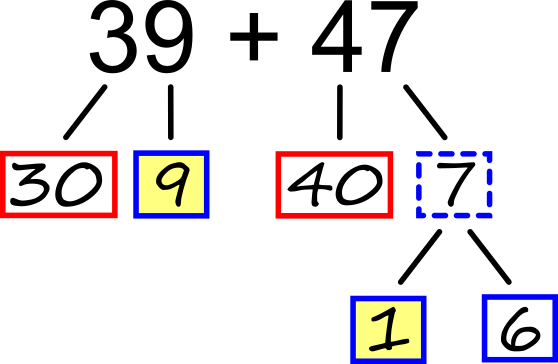
Seštevanje s prehodom
​

Desetice enostavno seštejemo:

• 30 + 40 = 70

Ko pa seštejemo enice, ugotovimo, da imamo prehod čez desetico:

• 9 + 7 = 16

Zato enico drugega seštevanca (7) razdelimo še naprej in sicer tako, da del le-te z enico prvega seštevanca (9) tvori točno desetico (obarvano rumeno):

• 9 + 1 = 10

Od enice drugega seštevanca (7) nam torej ostane še 6, ki pa jo bomo prišteli čisto na koncu:

• 30 + 40 = 70
• 9 + 1 = 10
• 6 ostane od enice drugega seštevanca

Ko vse skupaj seštejemo, dobimo rezultat 86.

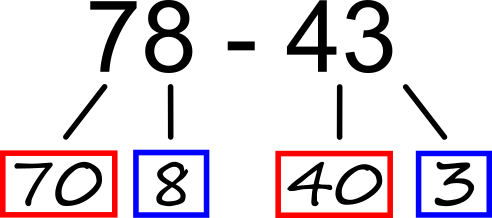
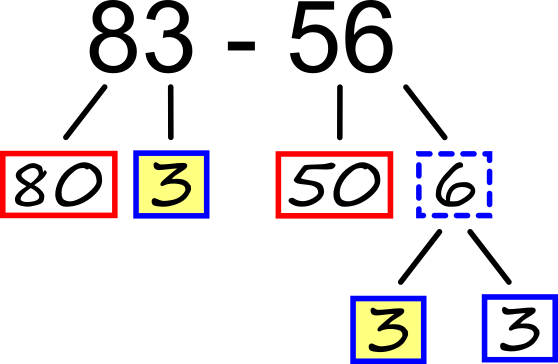
V našem primeru smo si ogledali prehod čez desetico. Na podoben način bi si lahko pomagali tudi pri prehodu čez stotico, tisočico ...

Odštevanje brez prehoda

Na podlagi drevesnega zapisa hitro ugotovimo:

• 70 - 40 = 30 in
• 8 - 3 = 5

Ko to dvoje seštejemo, dobimo rezultat 35. Prav se prebrali, seštejemo :) Desetice in enice smo seveda ločeno odšteli, a na koncu število vedno "zložimo" tako, da vrednosti, ki jih prispevajo posamezne desetiške enote (v našem primeru desetice in enice) seštejemo:

• 30 + 5 = 35

Odštevanje s prehodom
​

Če ne bi imeli prehoda, bi preprosto odšteli desetice in enice, tako kot v prejšnjem primeru. A Ker računa "3 - 6" v okviru naravnih števil ne moremo izračunati, smo enico odštevanca (6) razdelili še naprej in sicer tako, da se del le-te ujema z enico zmanjševanca (3, obarvano rumeno).

Račun nato izračunamo postopoma:

• 80 - 50 = 30
• 3 - 3 = 0 (obarvano rumeno); ta del lahko sedaj "pozabimo", saj na končni izračun ne vpliva (če številu prištejemo ali odštejemo 0, se ne zgodi nič)
• ​Od števil v okvirčkih nam je ostala samo še (neobarvana) 3 pri odštevancu, ki jo odštejemo od 30

Rezultat je torej 27.

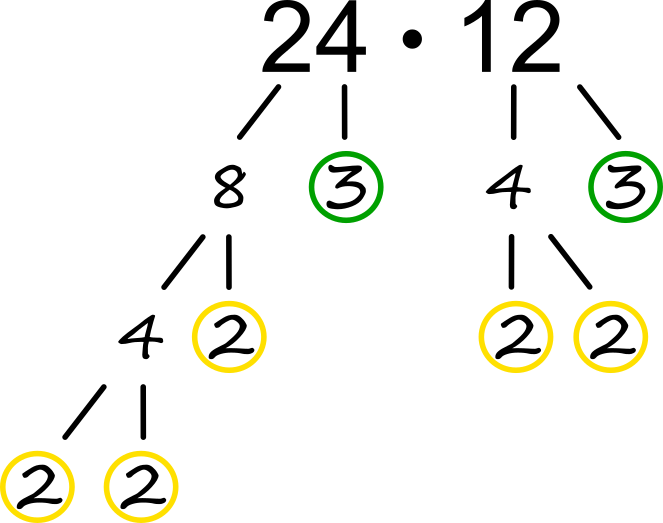
Dodatek: Če nalogo razširimo na cela števila, si lahko pomagamo s "trikom", ki je razložen tule.

Množenje

Če oba faktorja razcepimo na prafaktorje, rezultat lahko preprosto zapišemo v obliki potenc:

• 2∙2∙2∙2∙2 = 2⁵
• 3∙3 = 3²

Ko to dvoje zmnožimo, dobimo rezultat 2⁵∙3²

Rezultat lahko razmeroma hitro dobimo tudi z množenjem praštevil, kjer upoštevamo:

• vrstni red od večjih praštevil  proti manjšim (z vsakim množenjem je delni rezultat večje število, zato je bolje, da manjša praštevila pustimo za na konec)
• zmnožek praštevil 2 in 5 je 10, zato take pare z delnim rezultatom množimo skupaj (nov delni rezultat dobimo le z dodajanjem ničle na desno)

V našem primeru bi tako izračunali:

• 3∙3 = 9

• 9∙2 = 18
• 18∙2 = 36
• 36∙2 = 72
• 72∙2 = 144
• 144∙2 = 288

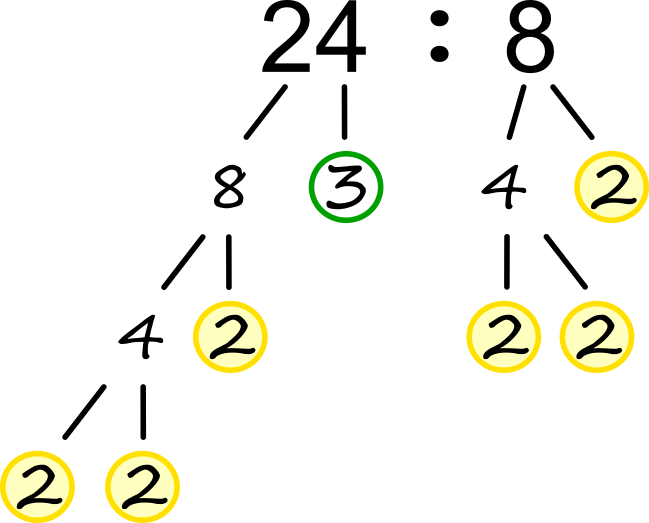
Do rezultata seveda lahko pridemo tudi s pisnim množenjem, kjer pa si s številskimi drevesi lahko pomagamo le v manjši meri.

Deljenje

Tako kot smo pri odštevanju ločeno odšteli desetice in enice, lahko pri deljenju enako storimo s prafaktorji, ki smo jih dobili s praštevilskim razcepom deljenca (24) in delitelja (8), saj je koncept odštevanja in deljenja zelo podoben.

Račun izračunamo postopoma:

• 2 (z leve, zapolnjen krog) : 2 (z desne, zapolnjen krog) = 1 (ponovimo 3-krat, nato pa ta del lahko "pozabimo", saj na končni izračun ne vpliva (če število množimo ali delimo z 1, se ne zgodi nič)
• na levi strani nam tako ostane le še 3, ki jo delimo z 1∙1∙1 (=1), ki je po trikratnem deljenju z 2 ostala na desni

Rezultat je torej 3.

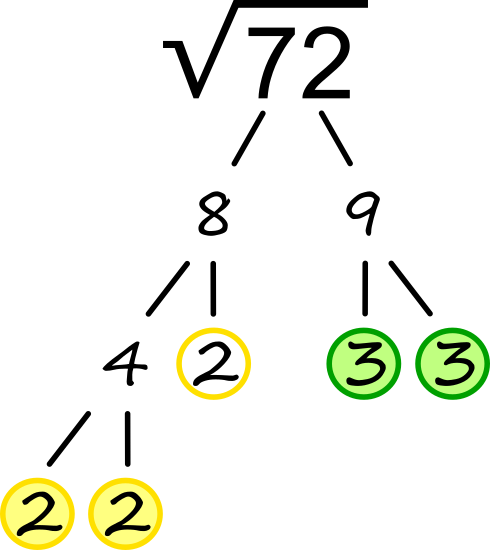
Za razmislek: Ob upoštevanju, da je deljenje je isto kot krajšanje ulomkov, s pomočjo številskih dreves skušaj okrajšati ulomek 24/8.

Delno korenjenje

Če število pod korenom razcepimo na prafaktorje, ga lahko zapišemo v obliki potenc:

• 72 = 2∙2∙2∙3∙3 
  

Ker vemo, da je kvadratni koren kvadrata števila enak številu samemu (√a²=a), ob upoštevanju pravil za korenjenje kvadrate števil lahko "vzamemo izpod korena". Pred tem moramo prafaktorje le še ustrezno grupirati:

• 2∙2∙2∙3∙3 = 2²∙2∙3²

Grupirani prafaktorji so označeni z zapolnjenimi krožci.

Končni rezultat je torej: √72 = √2²∙2∙3² = 2∙3√2

Pod korenom je ostal prafaktor 2, ker "nima svojega para".