Običajno iščemo najmanjši skupni večkratnik malih števil, rezultat pa je običajno neko veliko število (kljub temu, da govorimo o najmanjšem skupnem večkratniku). No, vsaj oznaka v (mala črka) je "v sorodu" z nečim malim.

Iskanje najmanjšega skupnega večkratnika si lahko poenostavimo na naslednji način:

• razcepimo podana števila na prafaktorje (začnemo z 2, nadaljujemo s 3, 5 in 7,...dlje nam običajno ni potrebno iti
• enake prafaktorje posameznega števila zapišemo s potenco
• obkrožimo vse prafaktorje z najvišjim eksponentom (ne glede na to, kateremu številu pripadajo)
• zmnožimo obkrožena števila in dobimo najmanjši skupni večkratnik podanih števil

Običajno iščemo največji skupni delitelj velikih števil, rezultat pa je običajno neko malo število (kljub temu, da govorimo o NAJVEČJEM skupnem delitelju). No, vsaj oznaka D (velika črka) je "v sorodu" z nečim velikim.

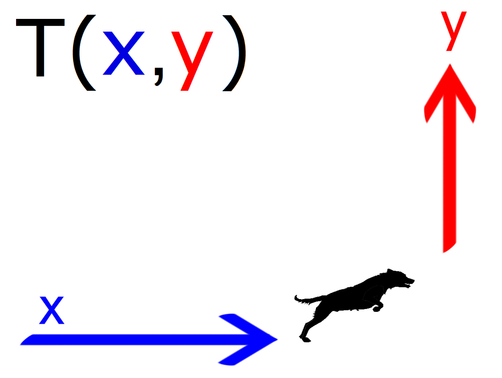
Poleg običajnega iskanja največjega skupnega delitelja si lahko pomagamo tudi s preprostim krajšanjem števil. Števila delimo s praštevili; začnemo z 2, nadaljujemo s 3 in 5...no, dlje nam običajno niti ni več potrebno iti. Števila krajšamo toliko časa, da nimajo nobenega skupnega delitelja več (pravimo, da so si tuja).
Če zmnožimo vsa praštevila, s katerimi smo krajšali prvotna števila, dobimo največji skupni delitelj.

Zamislimo si psa, ki teče (od leve proti desni) in nato skoči.

Tek psa je v vodoravni smeri. Vodoravna smer predstavlja x os na (kartezičnem) koordinatnem sistemu v ravnini.
Skok psa je v navpični smeri. Navpična smer predstavlja y os na (kartezičnem) koordinatnem sistemu v ravnini.

Sedaj pa logika:

Pes mora najprej teči, da lahko skoči. Tudi x se v abecedi nahaja pred y.
Torej je prva koordinata točke x, druga pa y:
​

Ste vedeli, da je deljenje enako ulomku?

Spomnite se na tipko za deljenje na kalkukatorju - združuje znak ":" za deljenje ter "-" za ulomek.

Tudi razmerje med dvema količinama zapišemo z znakom za deljenje oz. ulomek.

Obstaja preprost "recept":

1. Izpišemo količine, ki imajo podane številske vrednosti (to bodo naši podatki)
2. Ugotovimo, kaj iščemo (to bo naša neznanka, npr. "x")
3. Poiščemo relacije (oz. povezave) med podatki in neznanko
4. Zapišemo enačbo
5. Rešimo enačbo

V nadaljevanju vam predstavimo še nekaj najpogostejših tipov problemskih nalog.

Preverimo deljivost števca in imenovalca s praštevili.

Začnimo z najmanjšimi praštevili:

• z 2 je število deljivo, če se konča z 0, 2, 4, 6 ali 8
• s 3 je število deljivo, če je vsota števk deljiva s 3
• s 5 je število deljivo, če se konča z 0 ali 5

V praksi na ta način lahko že zelo učinkovito znižamo števili v števcu in imenovalcu.

Če ulomek še vedno ni okrajšan, nadaljujemo z večjimi praštevili (7, 11, 13, ...), a ta korak pogosto sploh ni več potreben.