|
Če postopka ne razumemo, nam ta predstavlja zgolj skupek navodil brez pomena. Če se med računanjem zmotimo, večinoma tega niti ne opazimo, ko pa se »zatakne«, nam pa ne preostane drugega, kot da vse skupaj pustimo in gremo reševat naslednjo nalogo. Ob razumevanju koncepta, ki se »skriva« za postopkom, pa lahko hitro opazimo, če gre kaj narobe, najpomembnejše pa je to, da se v primeru težav lahko sami »rešimo«. Oglejmo si postopek pisnega množenja z dvomestnim številom. Za primer vzemimo račun 123 · 45. Pri pisnem množenju 123 najprej množimo s 4, nato pa še s 5: Zakaj je spodnja vrstica (množenje s 5) zamaknjena v desno? V bistvu ni, ker je zgornja zamaknjena v levo. :) Zakaj? Zato, ker množenje s 4 v bistvu ni množenje s 4, ampak s 40 (več o tem nekoliko kasneje). S tem namenom sem na skrajno desno stran zgornje »zelene« vrstice tudi zapisal ničlo, a narahlo, saj jo (vsaj v naših šolah) ne pišemo. Prištevanje 0 v zadnjem koraku postopka, do katerega še pridemo, namreč ne spremeni končnega rezultata. Če je 123 · 4 enako 492, je 123 · 40 enako 4920, saj z 10 preprosto množimo tako, da na desni strani prvega faktorja pripišemo ničlo, 123 · 5 pa je 615. Na koncu »zeleni« vrstici še seštejemo in celotni račun se glasi: Zakaj moramo »zelena« zmnožka sešteti? Distributivnostni zakon pravi, da je zmnožek vsote dveh števil s tretjim številom enak vsoti posameznih zmnožkov prvih dveh števil s tretjim številom. Zapleteno? Prav imate. Zato sem o tem pripravil posebno razlago, kjer vam bo postalo vse jasno. :) Če število 45 razdelimo na desetice in enice, dobimo vsoto dveh števil iz našega zakona (ja, tistega, z neznansko zapletenim imenom :) ), števili med črtama pa sta posamezna zmnožka, za katera vemo, da ju moramo na koncu sešteti. In točno to v postopku tudi naredimo. Zapis z upoštevanjem distributivnostnega zakona se tako glasi: Dodatna vprašanja:
0 Comments
Naslov izgleda zapleteno, pri razlagi pa se bom potrudil, da ne bo tako :) Za pisno deljenje z dvomestnim številom obstaja več metod (za eno izmed njih sem posnel tudi video), tokrat pa si oglejmo metodo s približki. Metoda je primerna predvsem za delitelje z majhno oziroma veliko vrednostjo enice, saj je tu relativna napaka majhna in nam ne bo potrebno toliko radirati. Zakaj, si lahko ogledate tule, kjer sem to metodo uporabil pri delitelju 14 in sem imel kar veliko dela :) Mi pa izračunajmo naslednji račun: 279 : 31 Najprej ugotovimo, s kolikšnim delom deljenca pričeti računanje. Ker 31 ne gre v 27 niti enkrat, moramo vzeti vse 3 števke deljenca, zato »kljukice« (z njo ločimo del deljenca, na katerem izvajamo operacije, od preostalega dela) ne bomo potrebovali, s podpisovanjem pa bomo začeli pod enico deljenca. Za matematične navdušence (ostali lahko nadaljujete v naslednjem odstavku): Načeloma bi lahko začeli tudi le z dvema števkama najvišje mestne vrednosti (2 in 7), a bi bila prva števka količnika 0 (števka z najvišjo mestno vrednostjo), za 0 pred številom pa vemo, da je vseeno, če ga ni (za ničlo na najnižji mestni vrednosti pa seveda vemo, da mora biti tam). Računanje bomo torej pričeli z »delnim« računom 279:31 (v našem primeru je to kar celoten račun). Sedaj vas pa verjetno že zanima, kje se skriva približek iz naslova in zakaj ga sploh uporabimo. 279:31 je razmeroma težak račun, če pa 279 zaokrožimo na 280, 31 pa na 30, dobimo: 280 : 30 Če tako deljenec kot delitelj delimo z 10, se račun ne spremeni, zato dobimo nov, lažji račun: Spomnimo se na krajšanje ulomkov, za katere vemo, da so v bistvu računi deljenja: Tu lahko uporabimo znanje poštevanke, saj vemo, da je 9·3 enako 27, 10·3 pa 30. 28 je malo nad 27, torej lahko rečemo, da je 28:3 enako 9 »in še malo zraven«. Na tem mestu ne smemo pozabiti, da naš račun ni 28:3, ampak 279:31, zato računamo naprej na »originalnem« računu. Približek smo uporabili samo zato, da smo lažje ugotovili, približno (!) kolikokrat gre 31 v 279. Ker je 28 nekaj več kot 9·3 (oziroma 280 nekaj več kot 9·30), za 31 lahko rečemo, da gre približno 9-krat v 279 in zapišemo prvo števko količnika: 279 : 31=9? Ker smo prvo števko količnika ("uporabili" smo že celotni deljenec, zato je ta edina) zgolj ocenili, še nismo prepričani, da je prava, jo je potrebno preveriti z obratno računsko operacijo - množenjem (če število delimo in nato množimo z istim številom, dobimo nazaj prvotno število). Pozor: tega preverjanja z množenjem ne smemo mešati z množenjem v preizkusu, ki sledi na koncu računa, saj tu preverjamo vsako števko količnika posebej, v preizkusu pa celoten račun. Pa preverimo: 1·9 je 9 in nič ne manjka več do 9, zato pod enico deljenca zapišemo 0. 3·9 je 27 in nič ne manjka več do 27, zato tudi pod desetico deljenca zapišemo 0. Ostanka ni, saj je 31·9 enako 279, kar kasneje seveda lahko preverimo tudi s preizkusom. 279 deljeno z 31 je torej res 9. Ker sta bila naša približka (280 in 30) relativno blizu "originalnima" vrednostma (279 in 31), nam je "uspelo" že v prvem poskusu, sicer pa bi morali še malo radirati :)
Za konec še nekaj vprašanj za razmislek:
|
ARHIV
May 2024
KATEGORIJE
All
|
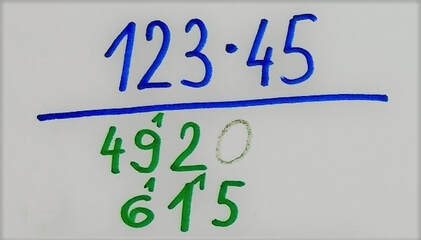
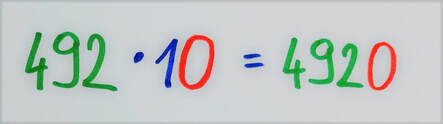
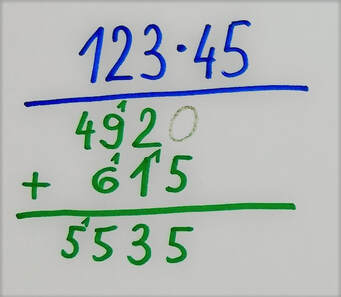
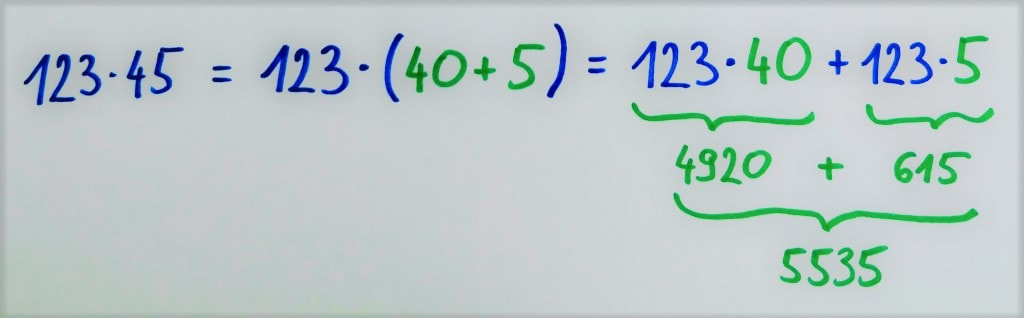
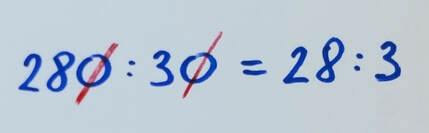


 RSS Feed
RSS Feed
