|
V nižjih razredih osnovne šole učenci še ne obvladajo "obračanja enačb", zato tako enačbe kot neenačbe rešujejo s poskušanjem. Pri enostavnih enačbah to nekako še gre, pri neenačbah pa se zadeva lahko kaj hitro "zavleče". Zato je koristno pri tem uporabiti nekaj logičnega sklepanja. Oglejmo si primer reševanja neenačbe x+2>=5:
Rešitev neenačbe x+2>=5 je torej x>=3. Opomba: Opisana metoda je primerna za reševanje neenačb v okviru množice naravnih števil + števila 0. Na tak način lahko rešimo enačbe s seštevanjem in odštevanjem, pri enačbah z množenjem in deljenjem pa je potrebna previdnost, predvsem če ulomki še niso bili obravnavani. V poštev v tem primeru pridejo samo določene kombinacije števil. Če je omenjena metoda prezahtevna, lahko za začetek poskusimo s tabelo, v katero vnesemo števila od 1 do 10 kot potencialne rešitve in nato eno po eno preverjamo, če ustreza. Ob tem lahko s pomočjo elaboracije preidemo na prvotno opisano metodo. Tule je še nekaj primerov za vajo: x > 3 x <= 7 x+2 > 5 x-2 <= 6 2+x >= 4 7-x < 5
0 Comments
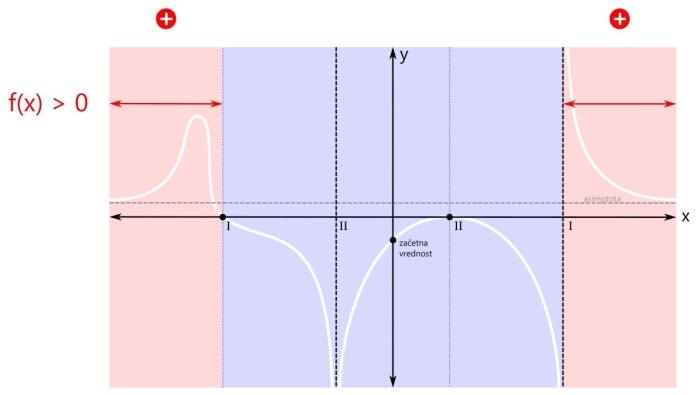
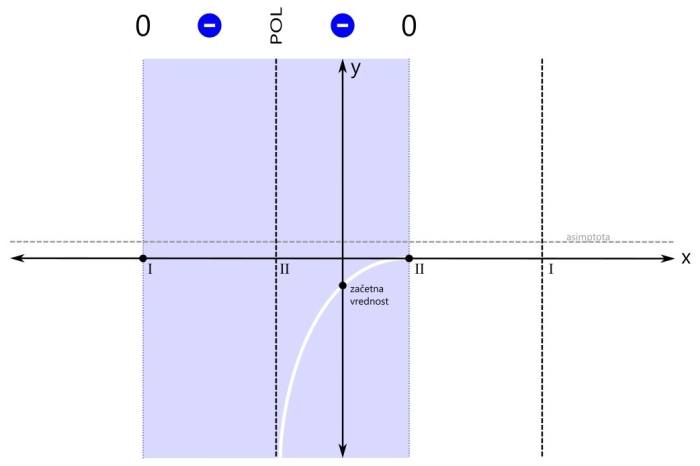
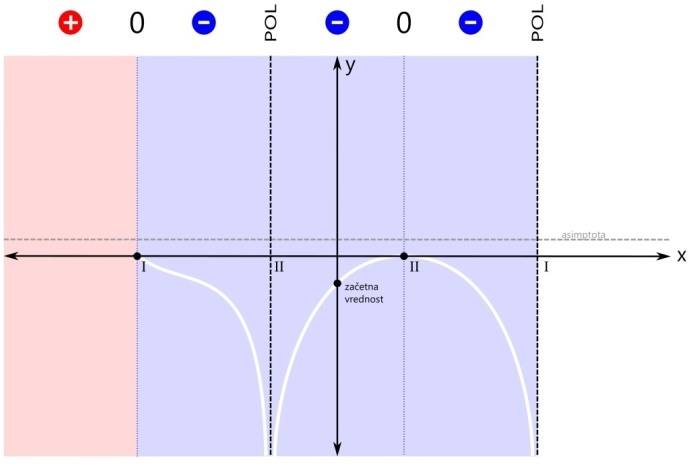
Povezavo si oglejmo kar na primeru grafa racionalne funkcije, ki smo ga narisali tule. Ogledali si bomo štiri značilne primere. V prvem primeru je pogoj za neenačbo vrednost racionalne funkcije (strogo) večje od nič. Zakaj "strogo"? Zato, ker ničla ni dovoljena ampak velja samo tisto, kar je večje od nič. Pozor! Pogoj govori o vrednostih y, medtem ko rešitev neenačbe podajamo v vrednostih x! Rešitev neenačbe običajno podajamo v enem ali več intervalih. Ker pogoj zahteva vrednost funkcije, večjo od nič, se osredotočimo na pozitivna (rdeča) področja. Taki področji sta dve, zato bosta v rešitvi dva intervala. Na sliki sta označena z rdečimi črtami, ki imata na krajiščih puščici. Zakaj puščici? Puščici na intervalu označujeta, da krajišči intervala nista vključeni v rešitev. Če bi bilo kakšno krajišče intervala vključeno v rešitev, bi bila tam pika. Na splošno so na krajiščih puščice v naslednjih primerih:
Pozor! Kadar je pogoj za neenačbo "strog", se vam ni potrebno ukvarjati z zgoraj omenjenimi pravili, ampak si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervala še z oklepaji. Pri tem upoštevamo:
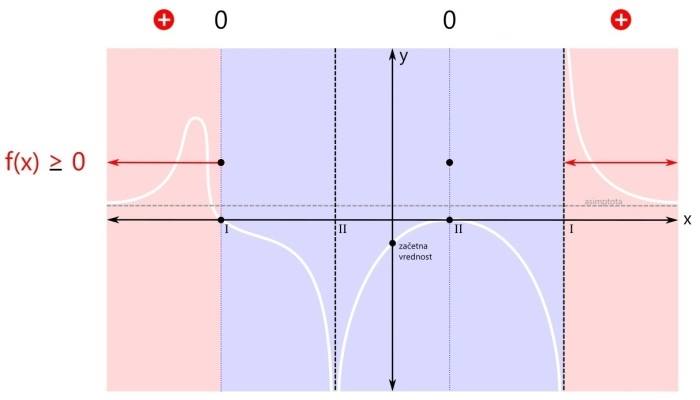
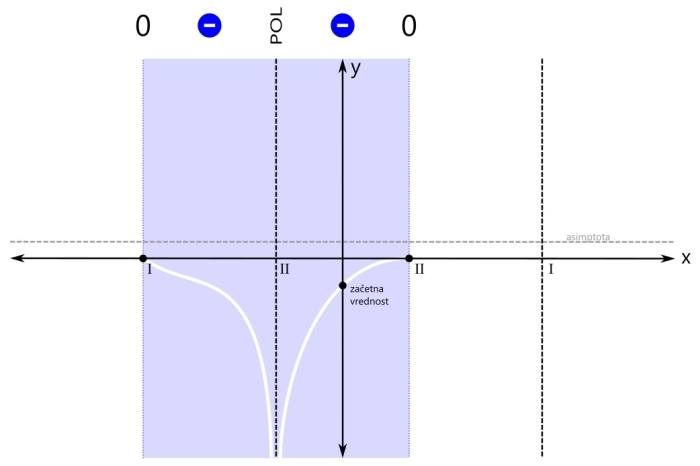
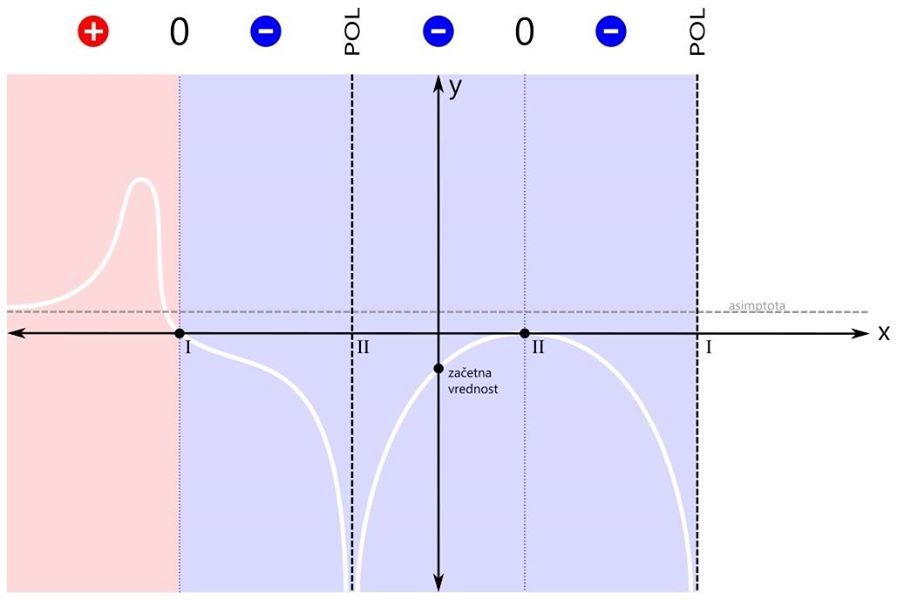
Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Med oklepaji je znak za unijo "∪". S tem znakom združimo intervale v eno rešitev. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desni pol pa na x=3, je v našem primeru rešitev naslednja: x ∈ (-∞,-3) ∪ (3,∞) V drugem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije večje ali enako nič. Od "strogega" pogoja se razlikuje v tem, da je ničla tu dovoljena. Tu pa nas zanimajo pozitivna (rdeča) področja ter ničle (črne pike):
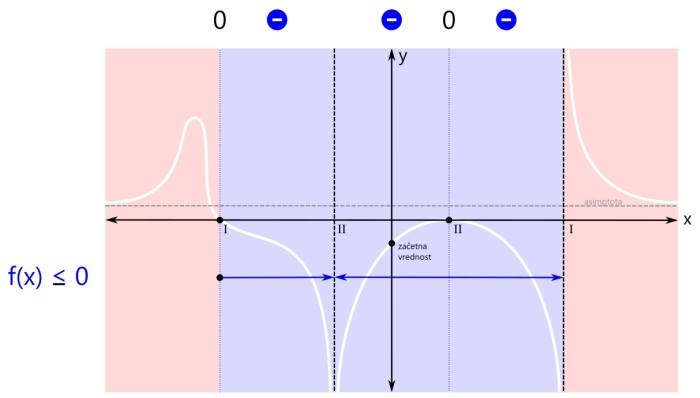
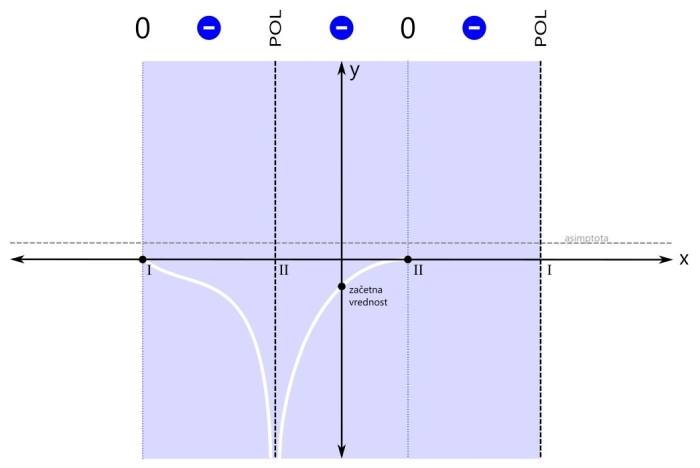
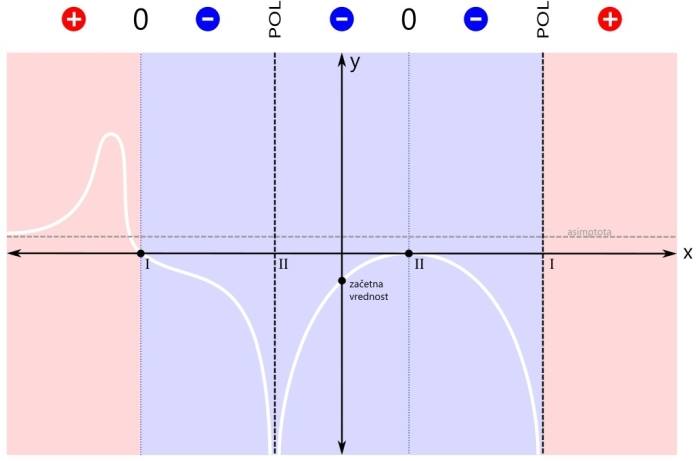
Ker sta rdeči področji dve, bosta v rešitvi dva intervala. Prva ničla (levo) je del prvega intervala (levo), zato je ni potrebno posebej navajati. Druga ničla (desno) pa je samostojna, zato jo je potrebno dodatno vključiti v rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, desna ničla na poziciji x=1, desni pol pa na x=3, je rešitev naslednja: x ∈ (-∞,-3] ∪ {1} ∪ (3,∞) Pozor! Ker je rešitev v desni ničli le ena točka, je ne podamo kot interval, ampak kot zapis posameznega elementa množice rešitev - v zavitih oklepajih. V tretjem značilnem primeru zapisa racionalne neenačbe je pogoj za neenačbo vrednost racionalne funkcije manjše ali enako nič. Tudi tu je ničla dovoljena. Kaj nas zanima? Negativna (modra) področja in ničle (črne pike):
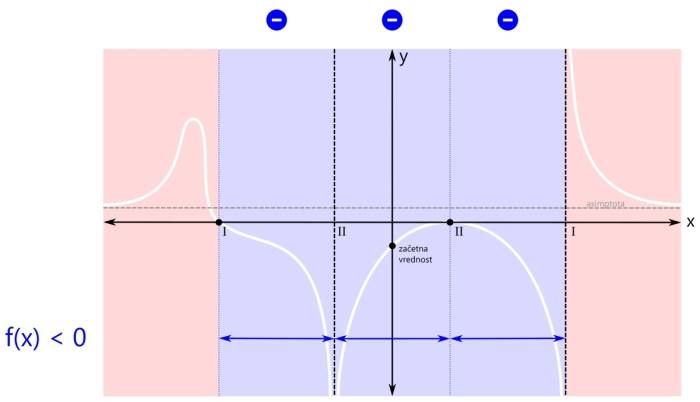
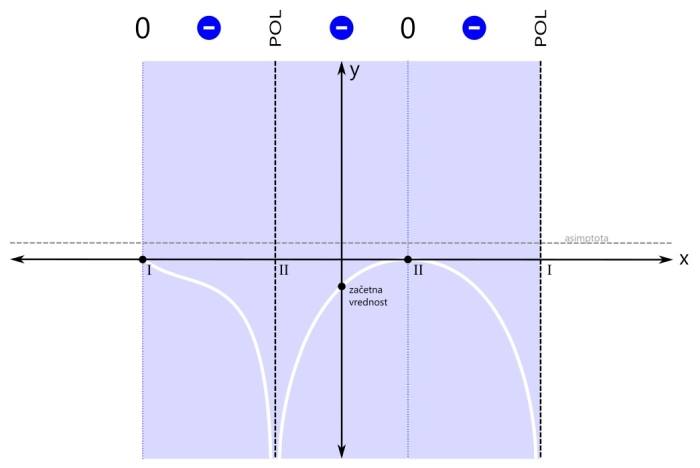
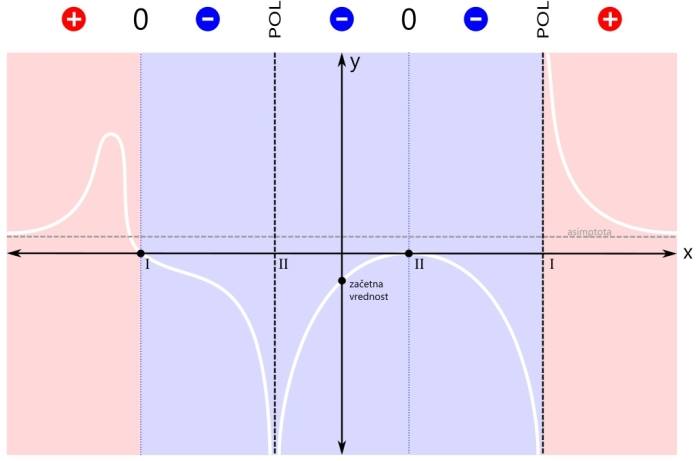
Ker so modra področja tri, bi bili v rešitvi načeloma trije intervali, a ker desna ničla združuje dva od njih, bosta v rešitvi le dva intervala. Ničla na skrajni levi pa je tudi del "modrega" intervala, tako da je ni potrebno navajati kot ločeno rešitev neenačbe. Grafična rešitev racionalne neenačbe je prikazana na spodnji sliki. Zapišimo rešitev še z oklepaji. Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desni pol pa na x=3, je rešitev naslednja: x ∈ [-3,-1) ∪ (-1,3) V zadnjem primeru neenačbe je pogoj vrednost racionalne funkcije (strogo) manjše od nič. Tako kot v prvem "strogem" primeru tudi tu ničla ni dovoljena. Velja samo tisto, kar je manjše od nič.
Ker pogoj zahteva vrednost funkcije, manjšo od nič, se osredotočimo na negativna (modra) področja. Tako področje je sicer eno samo, a je s polom in ničlo (druge stopnje) razdeljeno na tri dele. Rešitev bodo torej trije intervali. Na sliki so označeni z modrimi črtami, ki imajo na krajiščih puščice, kar pomeni, da krajišča intervalov niso vključena v rešitev. To, da so na krajiščih intervalov puščice in kdaj pike, smo že povedali, sedaj poudarimo samo naslednje: Pozor! Kadar je pogoj za neenačbo "strog", si enostavno zapomnite, da nobeno krajišče nobenega intervala ni vključeno v rešitev, torej imajo vsi intervali povsod puščice! Zapišimo intervale še z oklepaji. Ker imajo vsi intervali na krajiščih puščice, bodo vsi oklepaji okrogli. Še enkrat ponovimo naslednje splošno pravilo: Pozor! Kadar je pogoj za neenačbo "strog", so vsi oklepaji okrogli! Ker se leva ničla v našem primeru nahaja na poziciji x=-3, levi pol na x=-1, desna ničla pa na x=1, je rešitev naslednja: x ∈ (-3,-1) ∪ (-1,1) ∪ (1,3) Za vas smo pripravili "univerzalno" orodje, s katerim boste lahko kjerkoli in kadarkoli narisali graf racionalne funkcije ter reševali naloge s polinomi in racionalnimi funkcijami. Prvi se od slednjih razlikujejo predvsem po tem, da nimajo polov, s čimer so tudi njihovi grafi "lepši" :) Dobra novica pa je tudi ta, da si boste po branju tega prispevka omenjeni pripomoček lahko pripravili čisto sami :) Da bo pripomoček res univerzalen, ga pripravimo kar za racionalno funkcijo (za polinome ga bomo pa na koncu poenostavili). Naloge opisanega tipa običajno zahtevajo graf funkcije ali zapis rešitve neenačbe. Rešitev neenačbe je preprosto interval (pozor: na x osi!), kjer se graf nahaja nad ali pod določeno mejo. Predpostavimo, da ima naša racionalna funkcija dve ničli:
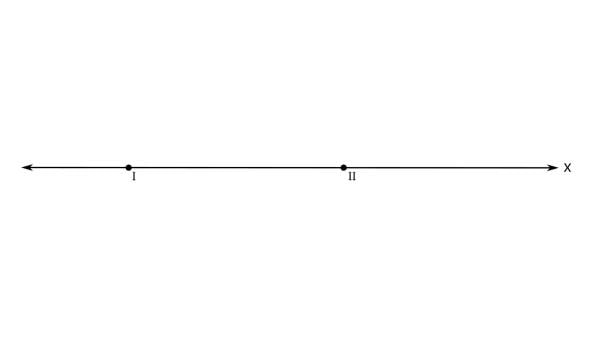
Računsko do teh ničel pridemo tako, da polinom v števcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=-3 in x₂=x₃=1. Narišimo x os in na njej označimo ničli (s pikama). Ničlo prve stopnje označimo z rimsko 1, ničlo druge stopnje pa z rimsko 2: Naša racionalna funkcija naj ima tudi dva pola:
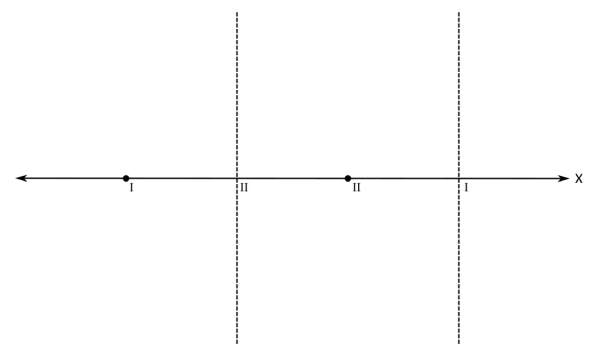
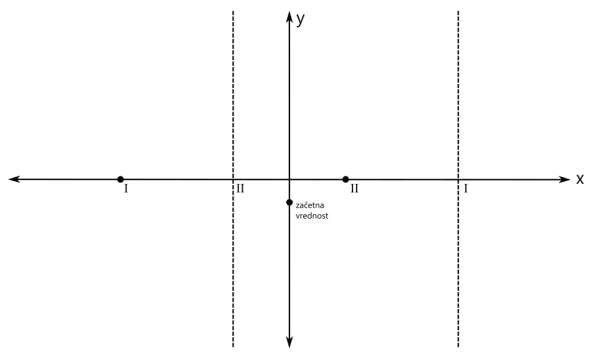
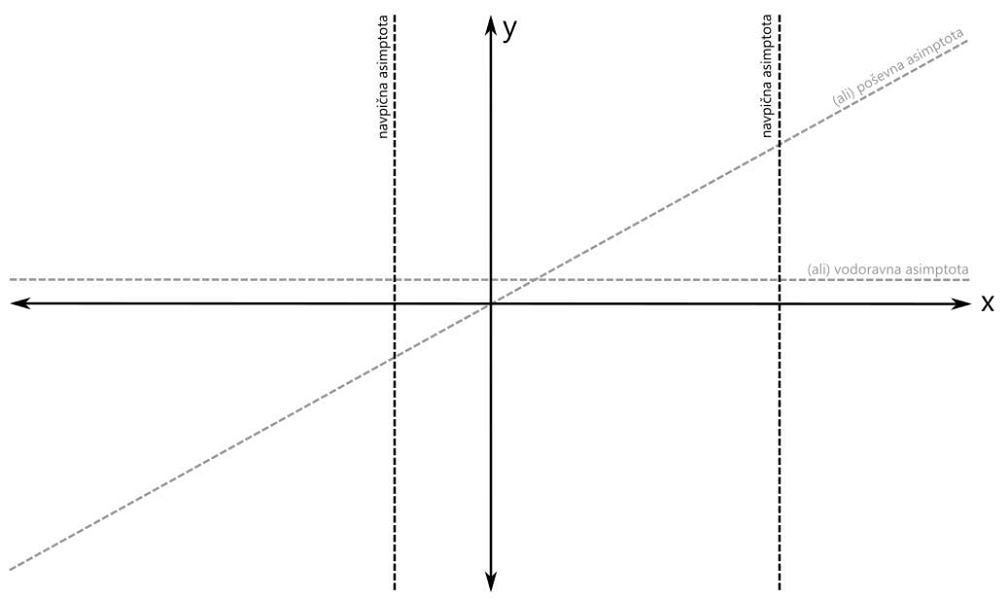
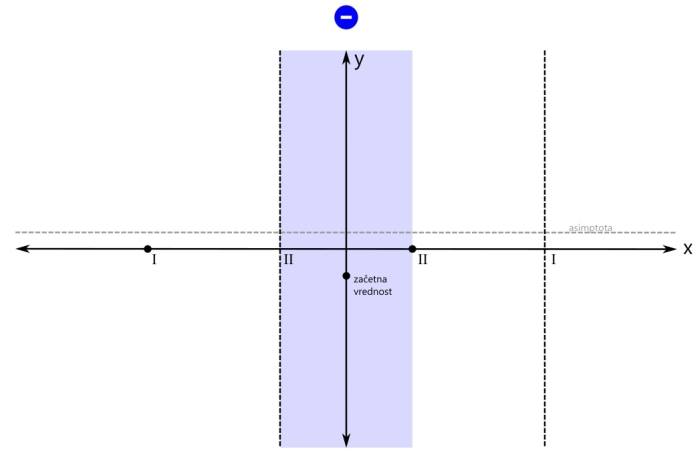
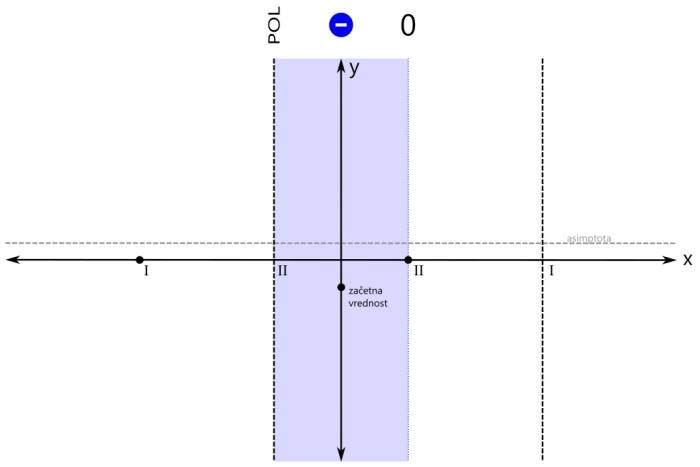
Računsko do teh polov pridemo tako, da polinom v imenovalcu racionalne funkcije izenačimo z 0 in rešimo enačbo. Z drugimi besedami, poiščemo ničle polinoma v imenovalcu. Ničla prve stopnje v rezultatu nastopa enkrat, ničla druge stopnje pa dvakrat. Na primer x₁=x₂=-1 in x₃=3. Ampak pozor! Kljub temu, da govorimo o ničlah, so na grafu to poli, saj gre za polinom v imenovalcu! Na x osi označimo še pola (z navpičnima črtkanima črtama). Pol prve stopnje označimo z rimsko 1, pol druge stopnje pa z rimsko 2: Ničle in pole naše racionalne funkcije smo označili, sedaj je na vrsti začetna vrednost. V našem primeru je začetna vrednost negativna. Pozor! Za razliko od vrednosti ničel in polov, ki sta bili vrednosti x, je začetna vrednost vrednost y! Na primer y=-0,5. Računsko do začetne vrednosti pridemo tako, da vse x v zapisu racionalne funkcije nadomestimo z 0 in izračunamo vrednost funkcije. Z drugimi besedami, začetna vrednost je količnik prostih členov polinomov v števcu in imenovalcu. Pozor! V primerih, ko se v x=0 nahaja kakšna ničla ali pol, je potrebno izbrati novo začetno vrednost, na primer pri x=-1 ali x=1. Narišimo še y os in na njej označimo začetno vrednost: Označimo še vrednost, ki jo naša funkcija doseže pri zelo majhnih oziroma velikih vrednostih x (po domače rečeno "levo oz. desno v neskončnosti", čeprav neskončnosti dejansko ne moremo doseči). To vrednost v koordinatnem sistemu predstavlja premica (lahko je tudi krivulja, a to spada že med zahtevnejšo matematiko), ki jo graf funkcije doseže na skrajni levi oz. desni strani (v "neskončnosti"). To premico imenujemo asimptota. Le-ta je lahko vodoravna (vodoravna asimptota) ali pa poševna (poševna asimptota). Pozor! Tako kot pri začetni vrednosti nas tudi pri asimptoti zanima vrednost y! Računsko do asimptote pridemo tako, da najprej preverimo stopnji polinomov v števcu in imenovalcu racionalne funkcije (to sta najvišja eksponenta x, ki se pojavita - pri potenci x², gre recimo za polinom 2. stopnje):
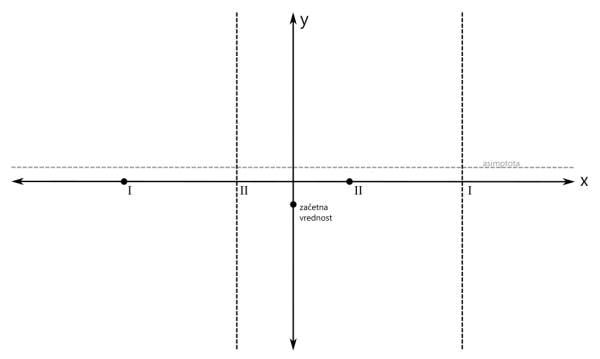
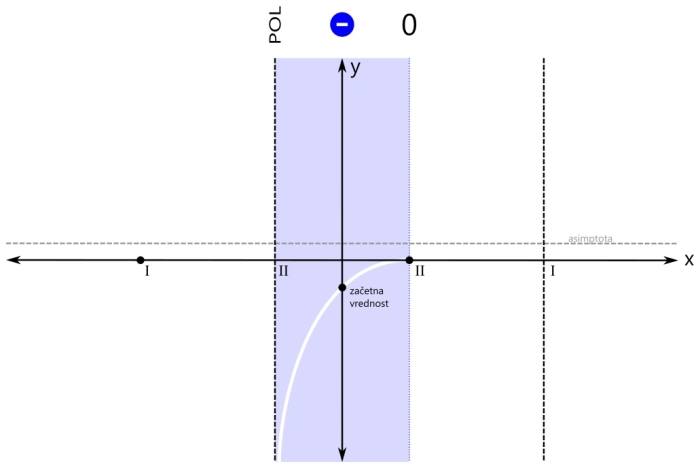
Pozor! Pri asimptoti je pomembno tudi to, da jo graf pri majhnih vrednostih x lahko seka, kar za pol recimo ne moremo reči. V našem primeru imamo vodoravno asimptoto, njena vrednost je pa večja od nič: Ustavimo se še nekoliko pri asimptotah. Po definiciji je asimptota premica ali krivulja, ki se v neskončnosti približuje drugi krivulji, ne da bi jo dosegla. Omenili smo vodoravno in poševno asimptoto. Ti dve asimptoti se nanašata na obnašanje grafa racionalne funkcije skrajno levo oziroma desno (-∞ oz. +∞ na x osi). Vodoravna in poševna asimptota hkrati ne moreta obstajati, saj se graf v neskončnosti lahko približuje le eni od njiju. Ne pozabimo: Vrednost vodoravne oz. poševne asimptote zapišemo kot y=... Pri risanju racionalne funkcije pa se skoraj vedno (kadar ima funkcija vsaj en realni pol) srečamo s še eno asimptoto, to je navpična asimptota. Ta je vedno navpična in poteka skozi pol racionalne funkcije. Navpične asimptote se nanašajo na obnašanje grafa racionalne funkcije v okolici polov (poli se nahajajo na x osi, graf pa gre v njihovi bližini navzgor ali navzdol proti neskončnosti). Navpičnih asimptot je za razliko od vodoravne in poševne lahko več - toliko, kolikor ima racionalna funkcija različnih realnih polov. Ne pozabimo: Vrednost navpične asimptote zapišemo kot x=... Navpičnih asimptot pri risanju grafa racionalne funkcije običajno ne omenjamo, le preprosto rečemo, da smo na koordinatnem sistemu označili pol racionalne funkcije. Je pa dobro, da vemo, da gre tudi v tem primeru za asimptoto. Vse asimptote rišemo kot črtkane premice. Tako, glavne značilne točke grafa imamo (stacionarne točke bomo izpustili), sedaj pa pričnimo z risanjem grafa. Graf bomo risali po odsekih, pred tem pa bomo na vsakem odseku določili predznak funkcije. Začnimo z odsekom okoli začetne vrednosti. Začetna vrednost je v našem primeru negativna, zato bo negativno tudi področje okoli nje. Za začetek z modro obarvajmo področje do prvega pola oz. ničle na levi oz. desni strani: Preverimo še predznak funkcije na robovih narisanega območja, označenega z modro barvo:
Sedaj pa pričnimo z risanjem grafa. Risali ga sproti z barvanjem območij predznaka funkcije. Zaenkrat imamo eno območje (modro). Začnimo pri začetni vrednosti. Pojdimo najprej v levo stran (do meje obarvanega območja). Ker se tam nahaja pol, graf zavije navzdol proti neskončnosti. Pozor! Navzgor graf ne more, saj bi pri tem sekal abscisno os, to pa drugje razen pri ničli ni dovoljeno! Na desni strani obarvanega območja pa imamo ničlo, zato začetno vrednost preprosto povežemo z ničlo na njeni desni. Pozor! Črta naj ne bo ravna, saj nimamo linearne funkcije! Pri risanju se izogibajmo še ostrim zavojem, pa smo že na dobri poti ;) Nadaljujemo v levo stran. Pol levo od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čezenj ne menja predznaka. Modro območje se tako nadaljuje vse do naslednje značilne točke grafa racionalne funkcije, to je ničla na skrajni levi. Vrednost funkcije v ničli pa je seveda nič ;) Nadaljujemo z risanjem grafa. Ostajamo v negativnem (modrem) območju, zato se graf vrne z iste strani, v katero je izginil, ko smo se približevali polu. Z grafom nato preprosto nadaljujemo proti ničli na levem robu modrega območja. Naj vas še enkrat opozorimo: črta naj ne bo ravna, saj nimamo linearne funkcije! Sedaj pa pojdimo še malo v desno stran. Ničla desno od začetne vrednosti je sode (druge) stopnje, zato funkcija pri prehodu čeznjo prav tako ne menja predznaka. Negativno (modro) območje se tako nadaljuje tudi v desno - do naslednje značilne točke grafa racionalne funkcije, pola na skrajni desni. Vrednost funkcije v polu pa ni definirana. Pozor! Zaenkrat naša racionalna funkcija nikjer ni pozitivna, kar pa ne pomeni, da je vedno negativna! V ničlah je vrednost funkcije nič, v polih pa ni definirana. Z risanjem grafa nadaljujemo v desno smer. Zopet smo v negativnem (modrem) območju, zato se graf desno od ničle obrne navzdol. Nadaljujemo v desno, do meje obarvanega območja. Ker se na skrajni desni nahaja pol, graf zavije navzdol proti neskončnosti. Ničla na skrajni levi strani je lihe (prve) stopnje, zato funkcija pri prehodu čeznjo menja predznak (iz negativnega v pozitivnega). Levo od te ničle ni nobene značilne točke grafa več, zato se pozitivno (rdeče) območje nadaljuje levo v neskončnost. Narišimo še zadnji odsek grafa na levi strani koordinatnega sistema. Ker se na skrajno levi ničli predznak funkcije zamenja (iz negativnega v pozitivnega), z grafom nadaljujemo levo od te ničle navzgor. Pozor! Navzgor ne pojdimo preveč daleč, saj se graf pri zelo majhnih vrednostih x (levo v neskončnosti) približuje vodoravni asimptoti! Zato naredimo "ovinek" navzdol in z grafom funkcije nadaljujemo naprej proti asimptoti. Če želimo graf na tem (rdečem) območju še točneje narisati, si lahko izberemo kakšno dodatno točko, v kateri izračunamo vrednost racionalne funkcije in jo vrišemo na koordinatni sistem (na primer f(-4), to je vrednost funkcije pri x=-4). Določimo predznak še na zadnjem območju grafa racionalne funkcije. Pol na skrajni desni strani je lihe (prve) stopnje, zato funkcija pri prehodu čezenj menja predznak (iz negativnega v pozitivnega). Desno od tega pola ni nobene značilne točke grafa več, zato se pozitivno (rdeče) rdeče območje nadaljuje desno v neskončnost. Narišimo še zadnji odsek grafa na desni strani koordinatnega sistema.
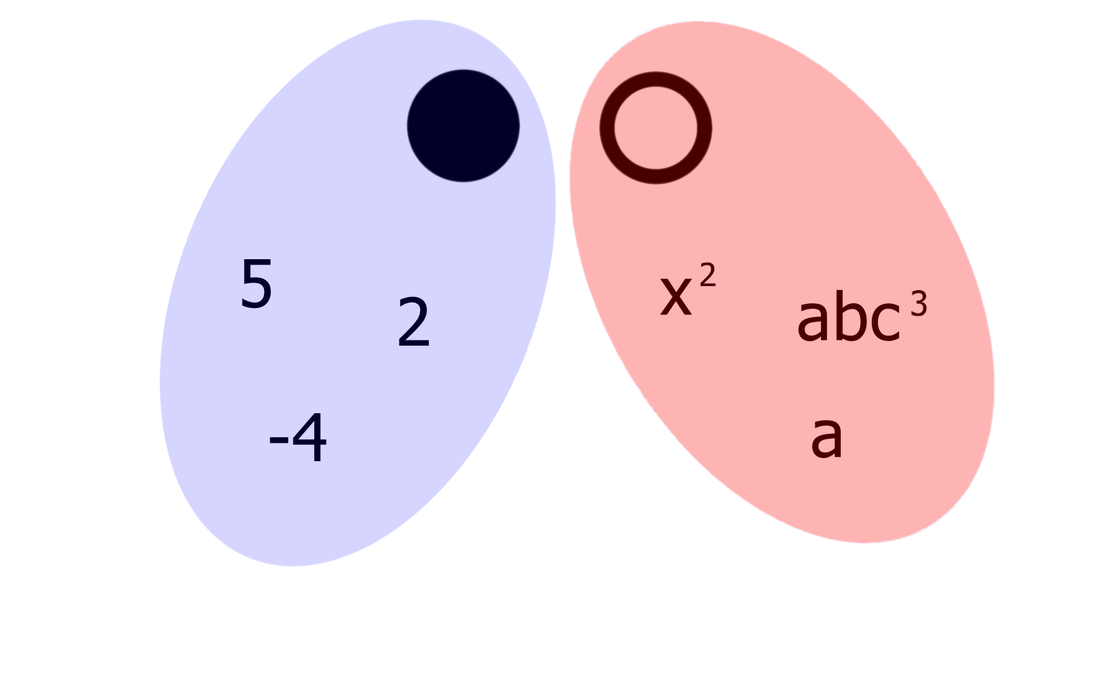
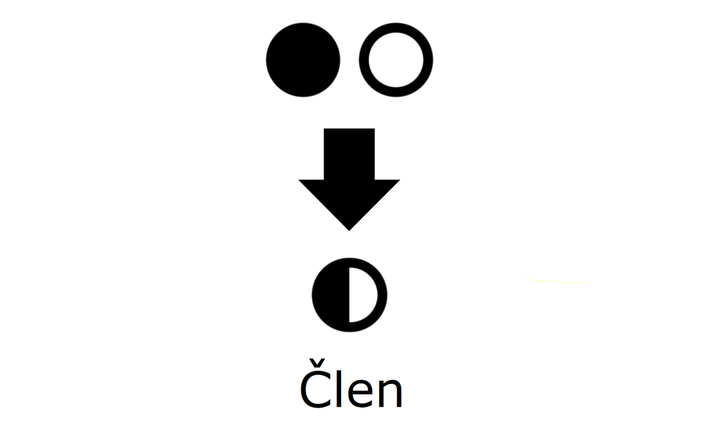
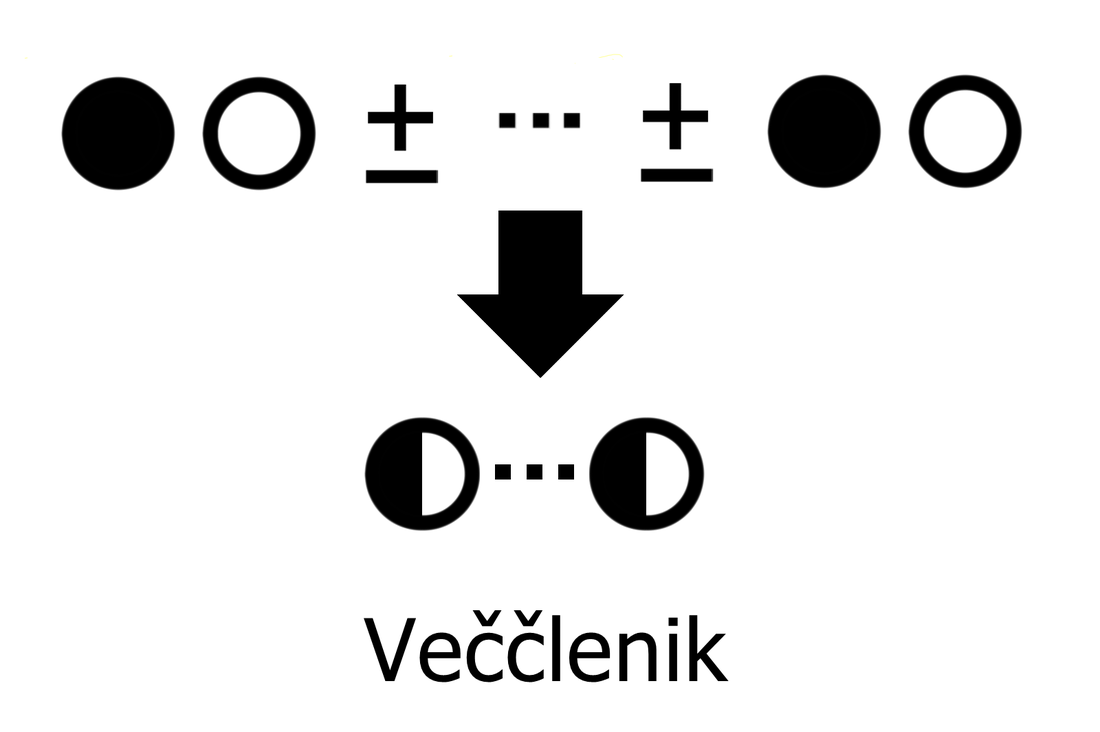
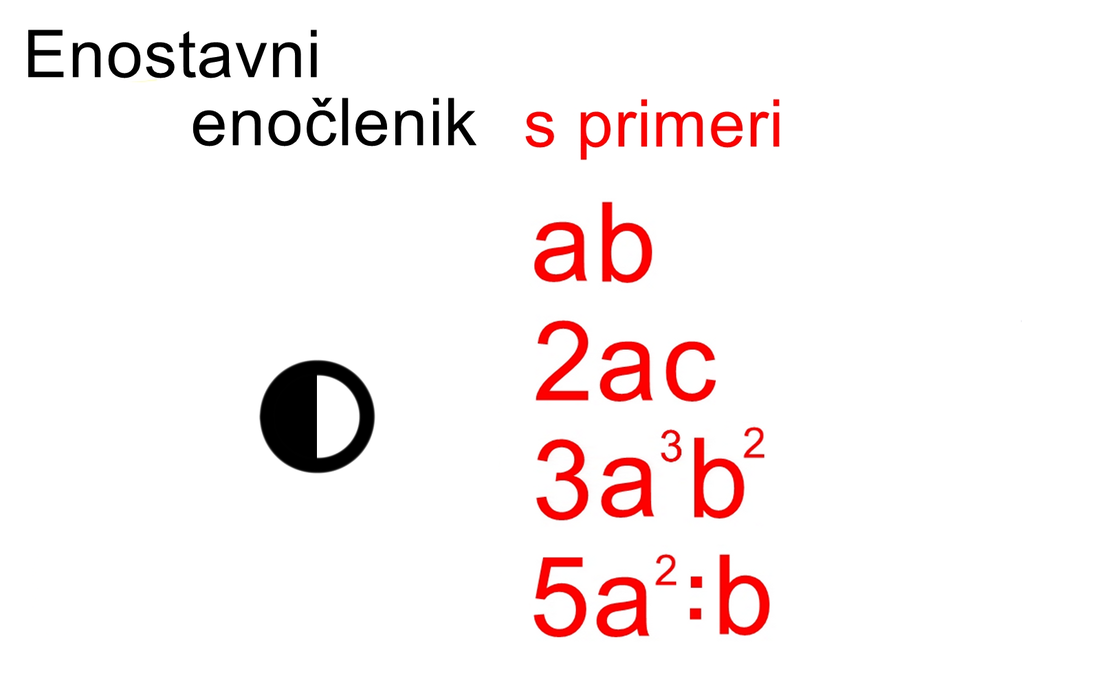
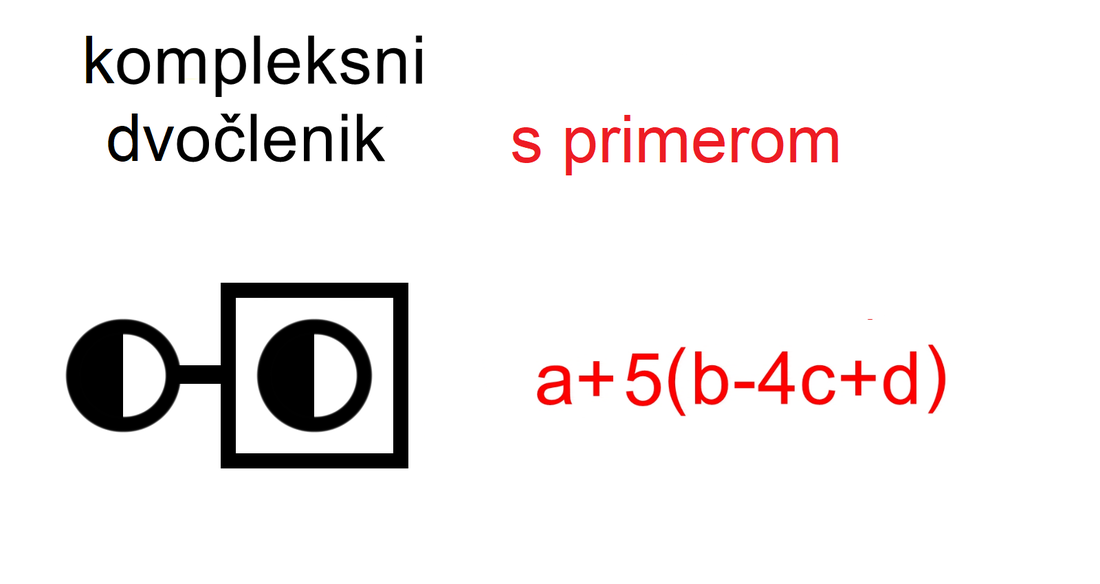
Ker se na skrajno desnem polu predznak funkcije zamenja (iz negativnega v pozitivnega), se graf na drugi strani pola ne vrne z iste strani, v katero je izginil (navzdol), ampak z nasprotne (od zgoraj). Ker se graf racionalne funkcije pri zelo velikih vrednostih x (desno v neskončnosti) približuje vodoravni asimptoti, le-ta naredi zavoj v desno (brez ostrih robov!) in se nadaljuje naprej proti asimptoti. Pozor! Abscisne osi (x) na tem odseku ne smemo več sekati, saj v področju desno od pola prve stopnje ni več nobene ničle, graf pa lahko seka abscisno os le pri prehodu preko ničle! Izrazi, enačbe, neenačbe, poenostavljanje, razstavljanje... Nočna mora za tistega, ki ne razume, "šala-mala" za tistega, ki "se mu posveti". Skozi nepregledno množico pravil se bomo tokrat skušali prebiti s pomočjo simbolov, kar bo všeč predvsem tistim, ki ste bolj "vizualni tip". Ponovitev Najprej ponovimo pojem "člen". Poenostavljeno rečeno je člen skupek številk in črk, med katerimi lahko nastopajo še simboli za množenje in deljenje ter eksponenti potenc in koreni. Ne pozabimo: znotraj člena simboli za seštevanje in odštevanje ter predznaka + in - ne nastopajo, razen če niso "ujeti" med oklepaje. So pa s simboli za seštevanje in odštevanje členi povezani med seboj! Definicija simbolov Začnimo z enočlenikom. Označimo ga z dvema krogoma:
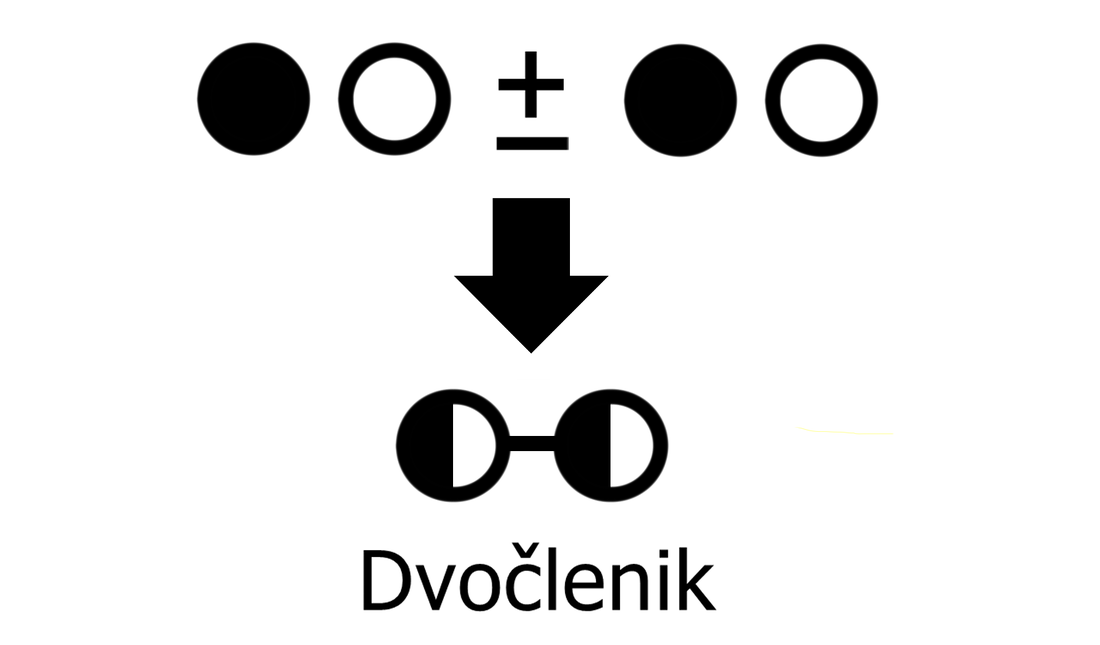
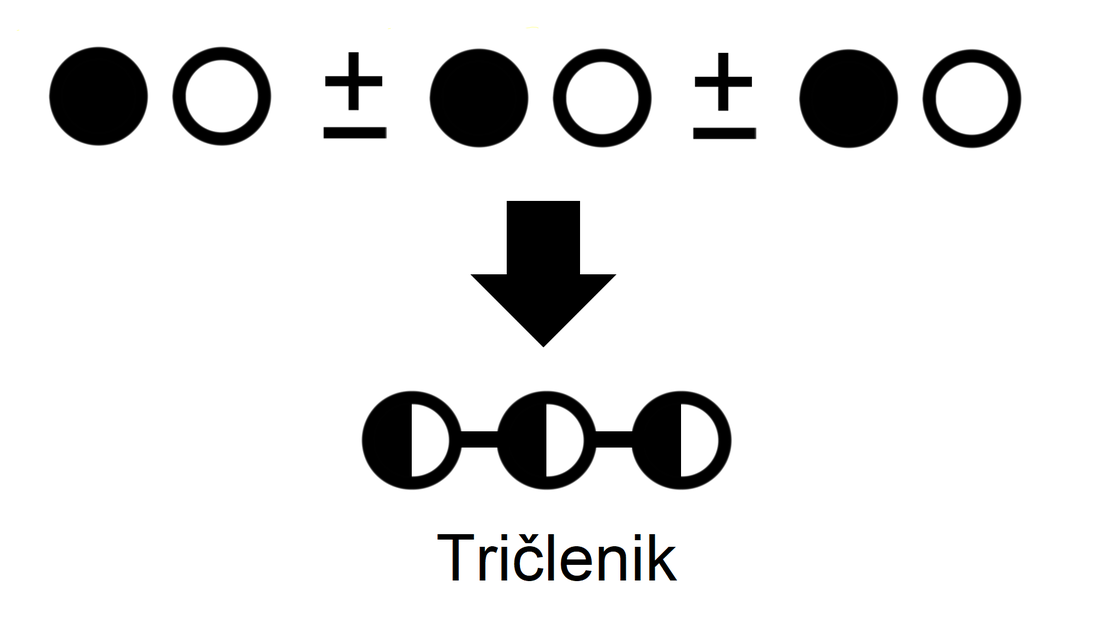
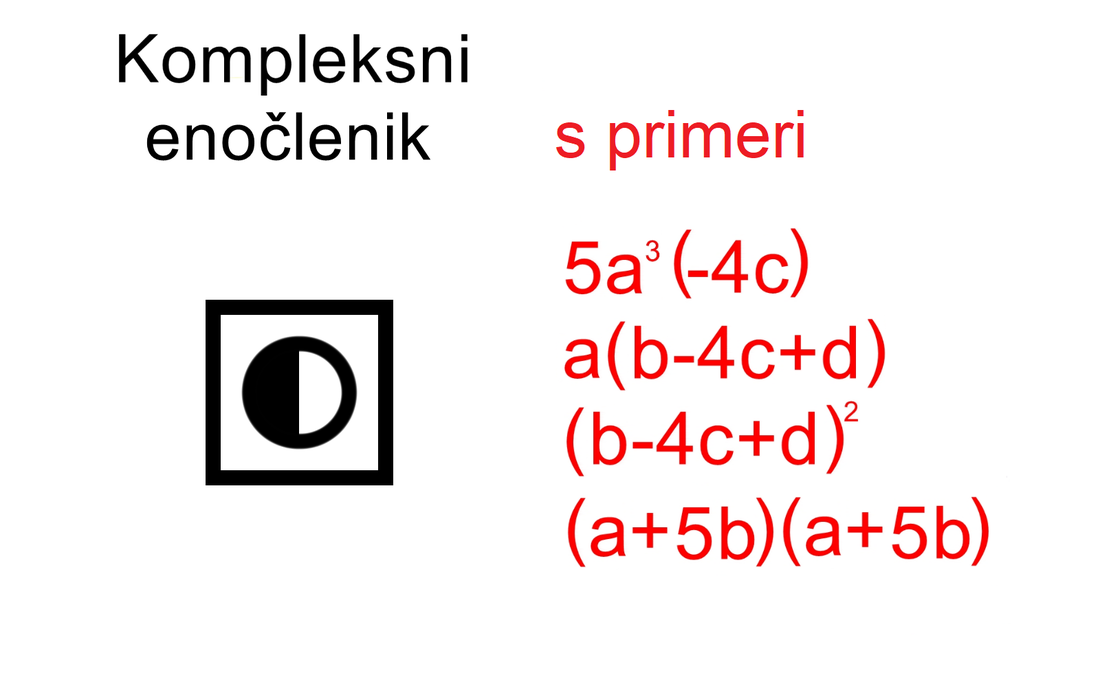
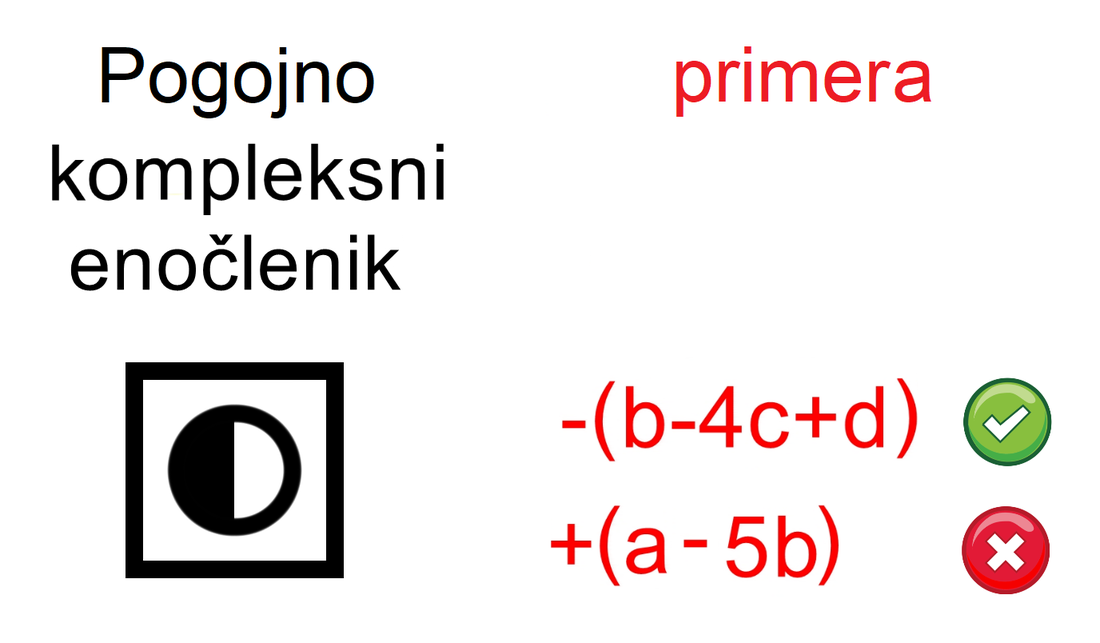
Če enočlenik ne vsebuje spremenljivke (take izraze srečamo v aritmetiki - samo številke, brez črk), rišemo le poln krog. Za boljšo preglednost lahko kombinacijo polnega in praznega kroga poenostavimo: Če med dva člena zapišemo + ali -, dobimo dvočlenik. Mi ga bomo označili takole: V izrazih se pogosto pojavlja tudi tričlenik: Ker je število členov lahko poljubno, dodajmo še simbol za veččlenik: Enočlenika običajno ne predstavljata le koeficient in spremenljivka (številka in črka, na primer 5a), ampak je sestavljen iz več delov, pogosto z oklepaji (na primer a(b-c)(d+e)). Tak enočlenik bomo poimenovali "kompleksni enočlenik". Seznam vseh simbolov je na naslednji sliki: Primeri zapisov s simboli Oglejmo si nekaj primerov za enostavni in kompleksni enočlenik: Če imamo le en oklepaj in pred njim stoji minus, je enočlenik pogojno kompleksni, saj gre v tem primeru za množenje oklepaja s številskim koeficientom -1 (posledično se po odpravi oklepaja vsem členom v oklepaju spremeni predznak): - (b-4c+d) = (-1)·(b-4c+d) = -b+4c-d Če pa pred oklepajem stoji plus, enočlenik ni kompleksen, saj oklepaj v tem primeru sploh ni potreben: + (a-5b) = a-5b Če enostavni in kompleksni enočlenik združimo v dvočlenik, dobimo: Zapis računskih pravil s simboli
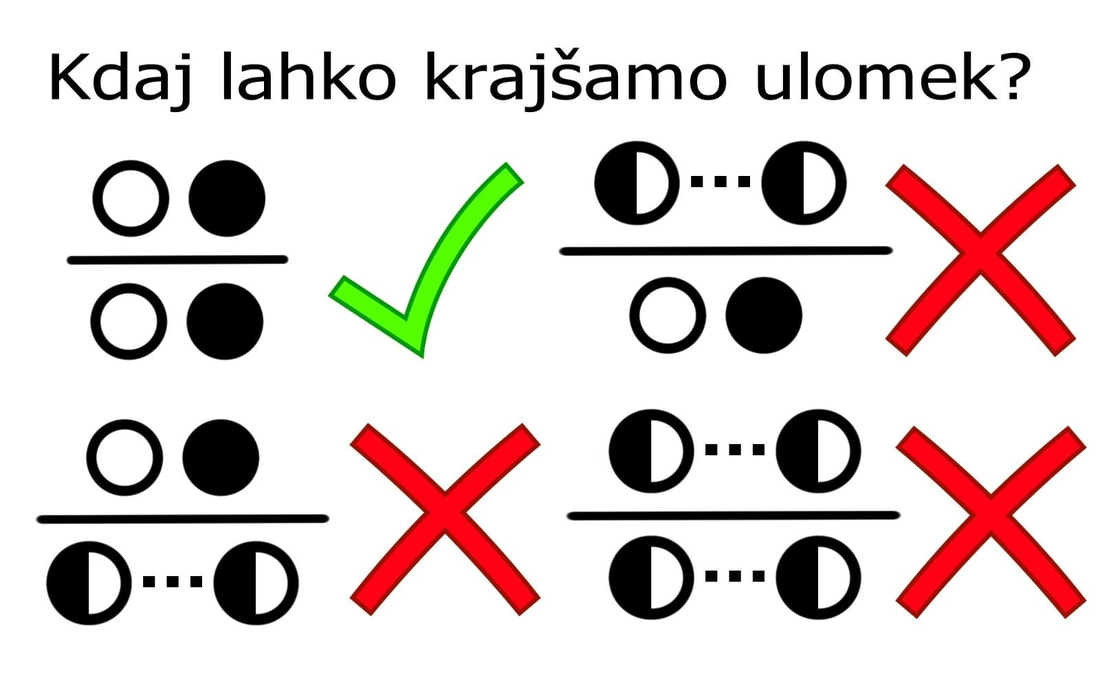
Za primer si oglejmo zapis pravila za krajšanje ulomkov. Ulomek lahko krajšamo samo takrat, kadar je tako v števcu kot v imenovalcu enočlenik. Kadar imamo opravka z veččleniki, jih je potrebno najprej razstaviti: |
ARHIV
May 2024
KATEGORIJE
All
|


 RSS Feed
RSS Feed
