|
Pravijo, da slika pove več kot 1000 besed: Že res, ampak tule vam vseeno malo pomagam. ;)
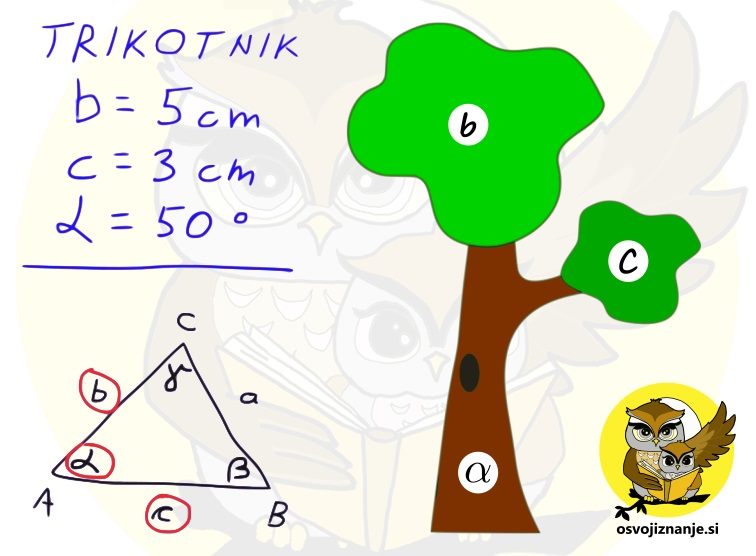
Slika predstavlja dokaj enostavni "recept" za načrtovanje geometrijskih likov, ki se glasi: "Najprej narišemo tisto, kar je vmes, nato pa še tisto, kar je na levi in na desni strani." V našem primeru pri trikotniku najprej narišemo kot alfa, nato pa na njem odmerimo še stranici c in b. "Logiko" si lahko zapomnimo s pomočjo drevesa. če hočemo priti do krošnje, moramo najprej splezati po deblu. ;)
0 Comments
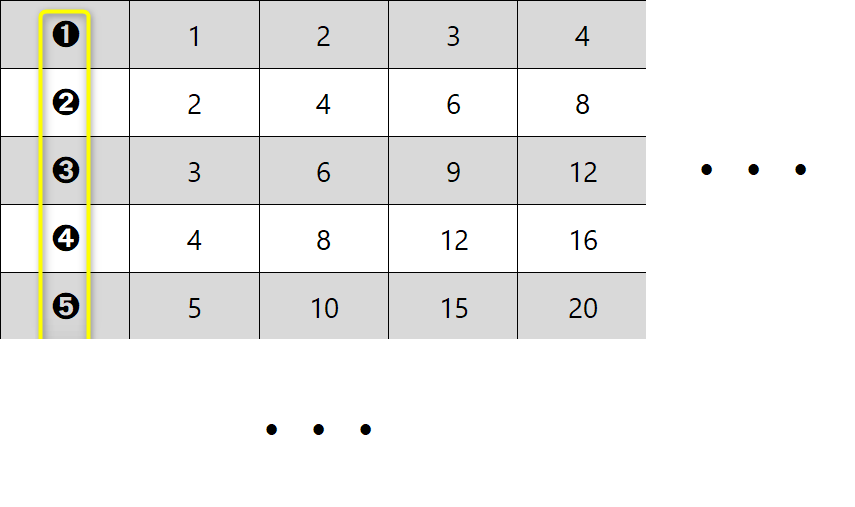
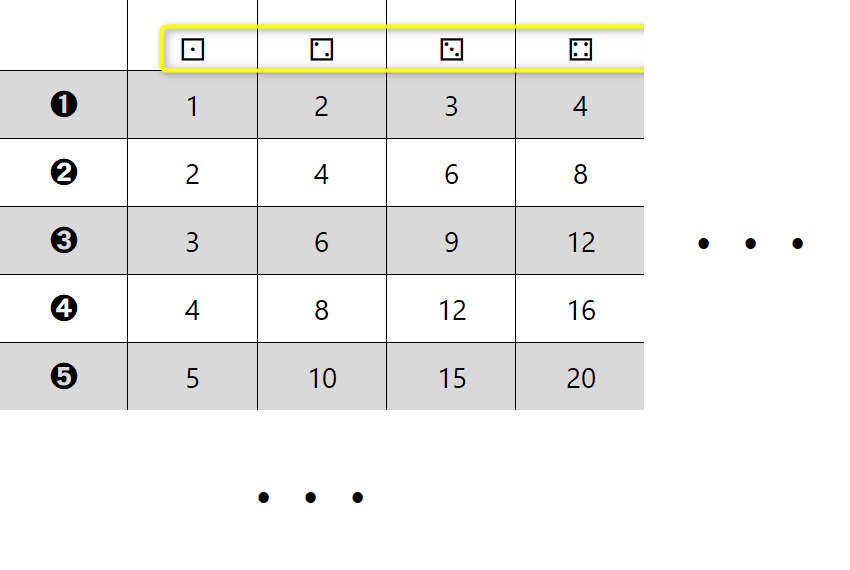
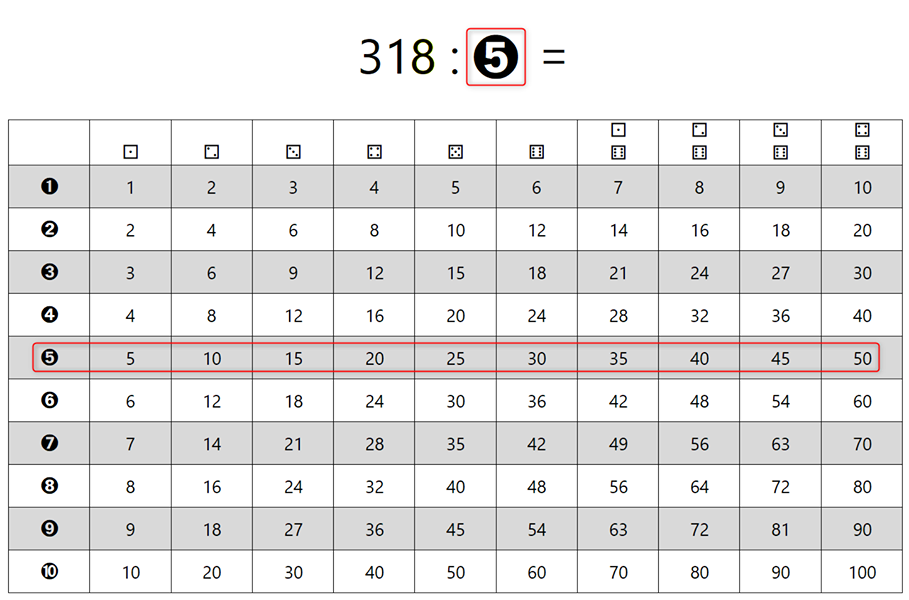
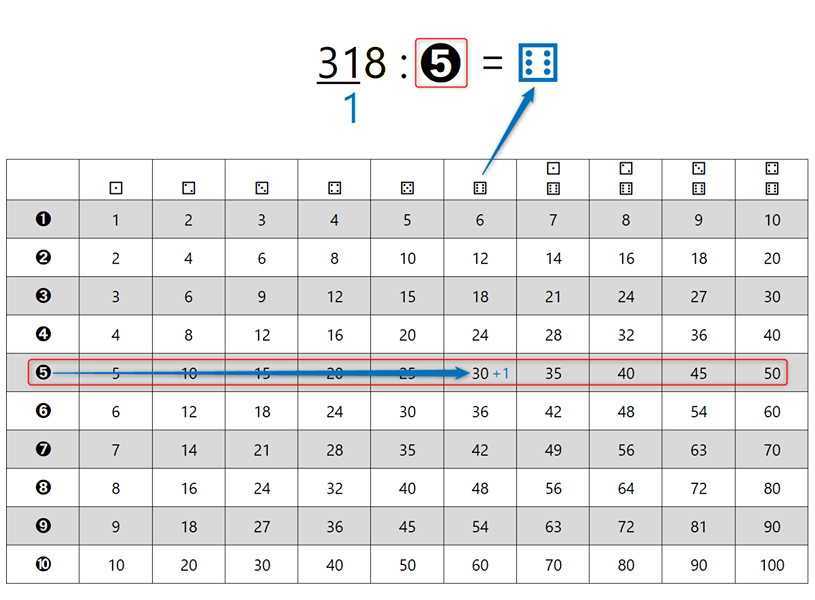
Naj vas najprej pomirim, tale pripomoček ni "potuha", če se je kdo slučajno ustrašil, je pa odličen "pomočnik" pri deljenju z ostankom in nam omogoča, da postopek tudi dejansko razumemo, ne le "znamo na pamet", kakor je na žalost dokaj pogosto pri poštevanki. Za 4 krat 5 vemo, da je 20, 20 deljeno s 4 pa je že problem. Kaj šele 21 deljeno s 4 ... Pri deljenju je ključno poznavanje večkratnikov delitelja (to je število, s katerim delimo oz. "tisto, kar stoji za dvopičjem" 😉). Zato celoten pripomoček temelji na večkratnikih števil. Zapišimo prvih 10 večkratnikov števil od 1 do 10 in sicer za vsako število v svojo vrstico tabele: Verjetno se vsi strinjamo, da se matematične pojme in postopke lažje zapomnimo, če jih povežemo z nečim znanim iz življenja. Nekaj takšnega so igralne kocke. Kot vemo, število pik pomeni vrednost, ki je "padla" ob metu kocke. Ena pika pomeni eno točko. Sedaj pa si predstavljajmo, da pika ni vredna eno točko, ampak več točk, od 1 do 10. To označimo tudi na naši tabeli - v prvi vrstici je pika vredna eno točko, v drugi dve in tako naprej do 10: Imena vrstic smo označili, preostanejo pa nam še imena stolpcev. Na podoben način, kot smo s številkami od 1 do 10 v krožcih označili vrstice, označimo tudi stolpce in sicer s kockami, na katerih je "padla" vrednost od 1 do 10. Ko na eni kocki "zmanjka pik", dodamo še eno kocko. Število pik na kocki pomeni, kateri večkratnik (po vrsti) števila v krožcu (v računu bo to delitelj) je zapisan v stolpcu pod kocko. Da bo razumevanje lažje, dodajmo še primer. Če na kocki padejo 4 pike (skrajno desni stolpec na sliki) in je vrednost posamezne pike 5 (spodnja vrstica na sliki), je skupna vrednost vseh pik 20, saj je 4 krat 5 enako 20. Velja seveda tudi, da je 20 deljeno s 4 enako 5 in 20 deljeno s 5 enako 4. Sedaj pa si oglejmo uporabo pripomočka na konkretnem računu deljenja z enomestnim številom, izračunajmo, koliko je 318 : 5. Ker delitelj (5) deli deljenca (318), bo iz deljenca nastalo več (enako velikih!) delčkov (in še nekaj ostanka). Število teh delčkov bomo zapisali desno od enačaja (to pa bo količnik). En tak delček je "vreden" 5 enot, ravno toliko, kot je "vreden" delitelj. "Po domače" nas zanima, koliko "petic" lahko "stlačimo" v škatlo, v katerem je prostora za 318 enot. Do rezultata najlažje pridemo tako, da poiščemo večkratnike delitelja, v našem primeru 5: Ker je 318 kar veliko število, bi morala biti spodnja tabela zelo široka, da bi v njej lahko našli rezultat. 🙂 Zato se reševanja lotimo postopoma. V vsakem koraku se bomo osredotočili le na prvih devet večkratnikov delitelja (dopustimo tudi 0), zato bo tabela z desetimi stolpci popolnoma dovolj. S tem postopkom v vsakem koraku dobimo eno števko rezultata oziroma količnika. Ker bomo račun reševali postopoma, je na začetku potrebno določiti, kolikšen del deljenca (318) bomo uporabili v prvem koraku. Izbiro začnemo z leve strani. Ker je vrednost prve števke (3) manj od 5 (delitelj), vzamemo prvi dve števki oziroma število 31. To število podčrtamo z vodoravno črto. Nadaljnji postopek pa je popolnoma enostaven:
Do sem je postopek dokaj standarden (morda le z izjemo načina označevanja stolpcev in vrstic v tabeli), medtem ko je naslednja ideja nekoliko bolj "smela". Pri prehodu na naslednji korak je potrebno določiti naslednji "mini" deljenec (v prejšnjem koraku je bilo to število 31 oziroma število, sestavljeno iz levih dveh števk števila 318). Običajno k ostanku v vrstici pod vodoravno črto (v našem primeru je to 1) prepišemo prvo števko od leve proti desni, ki ni podčrtana (v našem primeru je to 8) in dobimo naslednji "mini" deljenec 18. Naš predlog, ki bi si ga učenci verjetno lažje zapomnili, je naslednji: zakaj ne bi k ostanku v vrstici pod vodoravno črto "potisnili" kar celoten preostanek števila, ki ni podčrtan? V našem primeru je to sicer le števka 8, ampak če bi bil deljenec "daljši", bi pa lahko navzdol prestavili kar vse, kar ni podčrtano (trik: za lažje pomnjenje bi si predstavljali, da je delu deljenca "zmanjkalo tal pod nogami" 🙂 - to asociacijo bi si učenci lahko priklicali v spomin tudi, če bi postopek že nekoliko pozabili) S predlaganim pristopom je sicer v naslednjem koraku (in vsem, ki mu potencialno sledijo) potrebno znova določiti "mini" deljenca, a to ne bi smel biti prevelik problem saj za vse korake uporabimo enako logiko določevanja le-tega. Ponovimo postopek še za drugi "mini" deljenec (v našem primeru je to 18):
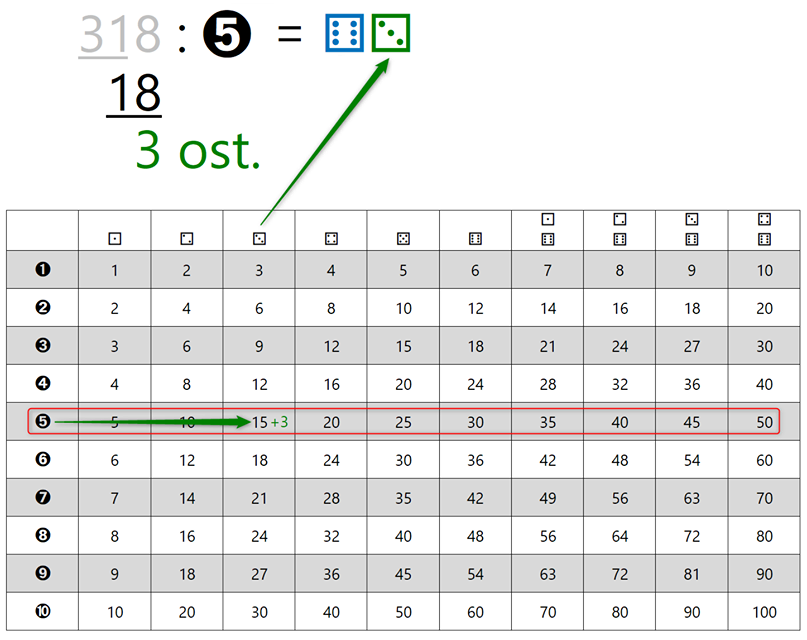
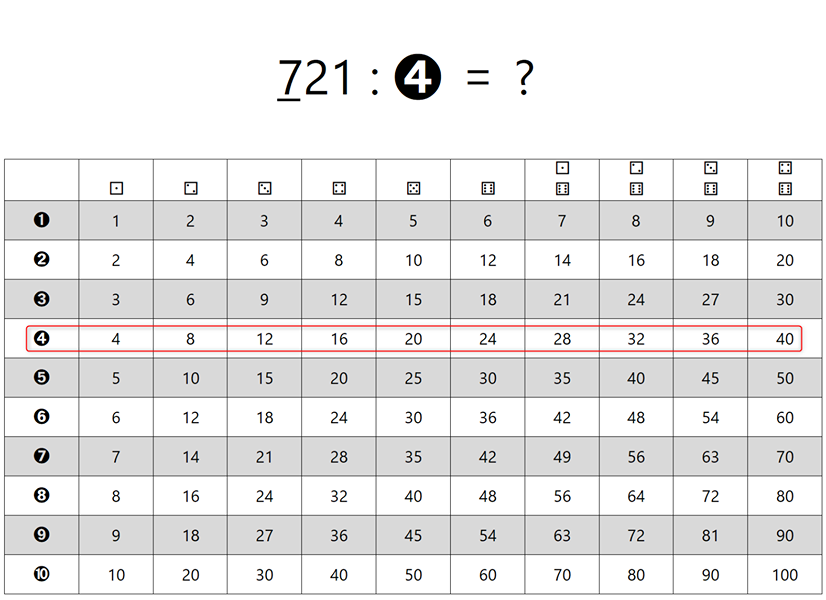
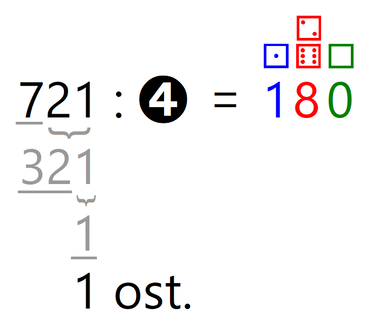
Ker desno od vodoravne črte ni nobene števke več (podčrtano je celotno število, s katerim smo delili oz. celoten "mini" deljenec, to je 18, zato nobeni števki ne more "zmanjkati tal pod nogami" 😉), smo z računanjem zaključili. Ostanek, ki smo ga dobili v zadnjem koraku deljenja (v našem primeru je to 3), je končni ostanek pri deljenju. Tega moramo v testu zapisati k rezultatu deljenja oziroma količniku, ki ga bomo iz kock "prebrali" pri zapisu končnega rezultata. Zapišimo še končni rezultat. Ostanek smo že določili, sedaj le še "preberimo" vrednosti kock. Število pik na kocki predstavlja vrednost posamezne števke, v našem primeru sta to 6 in 3, kar predstavlja število 63. V našem primeru, kjer smo število 318 delili s številom 5, smo torej dobili količnik 63 ter ostanek 3. Z drugimi besedami, v število 318 lahko "stlačimo" 63 petic, pa še ostane prostor za tri "vitke" enice. 😉 Naloga Izračunaj, koliko je 721 : 4. V tabeli je že označen "namig": Rešitev:
V našem primeru je druga vrstica nekoliko drugačna od tistega, kar se običajno uči v šolah (iz prve vrstice bi se namreč v drugo vrstico poleg ostanka 3 "morala po pravilih" prenesti le dvojka, ne pa celoten preostanek deljenca).
Pravilo sem nekoliko priredil, ker menim, da se učenci postopek lažje zapomnijo, če si predstavljajo, da preostanek števila, ki ni podčrtan, "pade v spodnje nadstropje" :) Kljub "mini spremembi" račun ni napačen, le potrebno je paziti, da v vsaki vrstici podčrtamo nov "vmesni deljenec", kar v "originalnem" postopku ni potrebno. Mogoče nekoliko razmišljanja več, a koraki so s tem poenoteni, kar pa tudi prispeva k lažji razumljivosti. Pazljivost je potrebna edinole v primerih, kjer pri deljenju vmesnega deljenca ni ostanka. Če v koraku, ki sledi, podčrtamo dve števki, je v rezultat potrebno "vriniti" še eno ničlo. Primer: 18300 : 6. Zakaj pa ne? :) Sicer ne dobesedno, ampak zavoj toast kruha je tako "matematičen", da grem težko mimo njega ;) Na njem si oglejmo nekaj količinskih predstav. Zamislimo si, da zavoj z desetimi rezinami kruha predstavlja tisočico. Če celotni zavoj kruha predstavlja tisočico, ena izmed rezin predstavlja desetino celotnega zavoja oziroma stotico. Tako kot deset rezin predstavlja celoten zavoj, deset stotic predstavlja eno tisočico. Mali otroci imajo radi kruh, narezan na "vojačke". En tak "vojaček" predstavlja desetino celotne rezine oziroma desetico. Tako kot deset "vojačkov" predstavlja celotno rezino, deset desetic predstavlja eno stotico. Kockice suhega kruha se odlično priležejo v juhi. Ena taka kockica predstavlja desetino "vojačka" oziroma enico. Tako kot deset kockic predstavlja celotnega "vojačka", deset enic predstavlja eno desetico. Raziskave kažejo, da si matematiko si najbolje zapomnimo na podlagi praktičnih primerov, zato pozorno opazujmo naravo okoli sebe in sigurno bomo našli še kaj uporabnega za naslednjo uro matematike. ;)
|
ARHIV
May 2024
KATEGORIJE
All
|

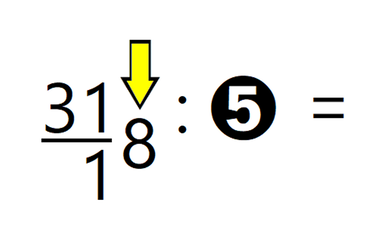





 RSS Feed
RSS Feed
