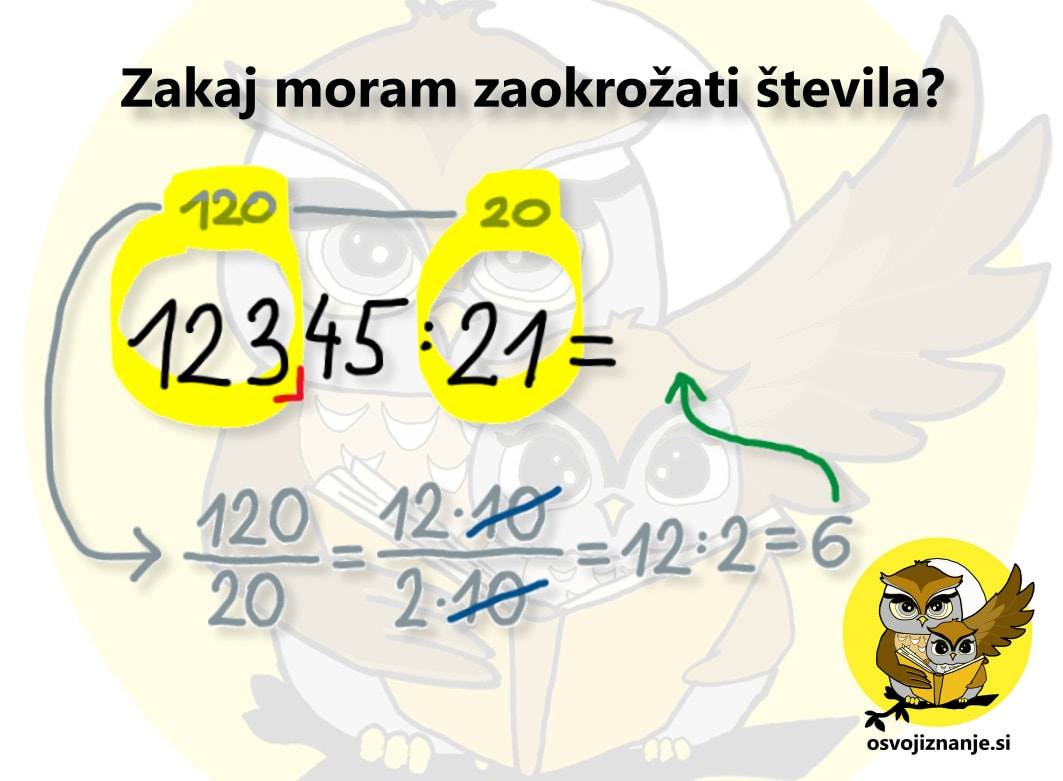
Ker pisno deljenje velja za postopek, v knjigah in na spletu mrgoli "kuharskih receptov" z vrstnim redom opravil, ki ga je potrebno dosledno upoštevati, če ne želimo npr. bankrotirati, ko bomo 100 evrov med 10 sodelavcev razdelili tako, da bomo vsakemu dali 1000 evrov. ;)

Tako kot življenje pa ne poteka vedno "po ravni črti", se tudi pri pisnem deljenju včasih kje ustavi. In če znamo zgolj postopek na pamet, je račun potrebno prečrtati in začeti znova.

"Tekoče znanje matematike" namreč ne pomeni, da znamo vse postopke na pamet, ampak je to sposobnost, da se "izmotamo iz težav", ko naletimo nanje. Recimo, da pozabimo korak postopka ali pa se pri prejšnjem koraku zmotimo. Takrat nam po glavi začnejo rojiti različna vprašanja in zaželimo si, da bi imeli ob sebi nekoga, ki bi ga lahko prosili za pomoč.

S tem namenom sem tokratni članek oblikoval v obliki vprašanj in odgovorov. Upam, da vam bo v pomoč. :)

Koliko števk deljenca (na levi) moram vzeti za prvi izračun?

Ravno prav. :) Pojdimo lepo po vrsti, pri tem pa si pomagajmo s primerom na sliki.

Kot vemo, je deljenje enako ulomku in ulomek s števcem, manjšim od imenovalca, je manjši od 1. V okviru celih števil je to 0 (v minus ne gremo). Če bi torej vzeli premalo števk (v našem primeru le prvo ali prvi dve), bi bil rezultat deljenja manjši od 1 in prva števka količnika (desno od enačaja) bi bila 0.  S tem sicer ni nič narobe, a je brez smisla, saj ničel pred števili ne pišemo. Tudi preveč števk (npr. prve štiri) ne bi bila dobra rešitev, saj bi bilo računanje preveč zahtevno, s čimer bi algoritem izgubil smisel.

V našem primeru je torej najbolje izbrati tri števke, s čimer je celoštevilski rezultat prvega deljenja enomestna vrednost (1, 2, 3 ... ali 9), v našem primeru 6. Ta vrednost je hkrati tudi prva števka rezultata (količnika) in jo bomo bomo zapisali desno od enačaja, kar bo razvidno v nadaljevanju.

Kako najlažje pridem do vrednosti, ki jo je potrebno podpisati na levi strani?
​
Že v prejšnjem poglavju smo ugotovili, da je razlika med zmnožkom »množenja nazaj« (105) in »trenutnega« deljenca (123) enaka 18, nismo pa povedali, kako do te razlike najlažje pridemo.

Na sliki je prikazana strategija s približevanjem preko »okroglih« števil (angl. under strategy). Za okrogla števila štejemo večkratnike potenc števila 10, v angleškem jeziku zanje pogosto slišimo izraz »friendly numbers«. Namesto te strategije bi lahko uporabili tudi strategijo s prištevanjem »okroglega« števila in vračanjem nazaj (angl. over strategy): 123 + 20 - 2.

Omenjen način je marsikomu mogoče nekoliko neobičajen, saj je navajen »klasičnega« računa odštevanja v stolpcu (123 - 105), ampak omogoča veliko boljši vpogled v sam koncept pisnega deljenja. Saj se tudi vprašamo ponavadi: »Koliko od 105 manjka do 123?« in ne: »Koliko je 123 minus 105?« :)

Kako pravilno podpisujem?

Pri podpisovanju si zapomnite predvsem to, da enico podpisanega števila zapišete točno pod enico »trenutnega deljenca«.  V našem primeru to pomeni 8 (enica števila 18) pod 3 (enica števila 123). Za lepši in bolj sistematičen izgled je seveda dobro zapisati tudi desetice pod desetice, stotice pod stotice itd., a za opisani način reševanja s pomočjo številskega traka to ni bistveno.

Pri prvem podpisovanju si lahko pomagamo tudi s »kaveljcem«, ki označuje konec »trenutnega deljenca« (v našem primeru stoji med števkama 3 in 4 deljenca), pri podpisovanjih, ki sledijo, pa pazimo na to, da gremo v vsakem koraku za eno mesto v desno.

Zakaj pa moramo paziti na to, da so enice pod enicami? Zato, ker bomo naslednjem koraku na desno stran podpisanega števila dodali naslednjo števko deljenca (v našem primeru je to števka 4), s čimer bomo dobili nov »trenutni deljenec«.  In če je podpisana vrednost zamaknjena v levo ali v desno, se nam lahko zgodi, da bomo na desni strani dopisali napačno števko (v našem primeru 3 ali 5), kar za naš račun ne pomeni nič dobrega. Več o tem povem v naslednjem poglavju o »padajočih števkah«. :)

Kaj pri pisnem deljenju »pada dol«?

Podpisovanju razlike med zmnožkom »množenja nazaj« in »trenutnega deljenca«  vedno sledi dodajanje naslednje števke deljenca na desno stran te razlike, s čimer dobimo »trenutni deljenec« za naslednji korak deljenja.

Ste kaj razumeli? Brez skrbi, z razlago ob primeru bo lažje. ;)

V našem primeru je razlika med zmnožkom »množenja nazaj« (21 · 5 = 105) in »trenutnega deljenca«  (123, na rumenem polju do rdečega »hakeljca«) enaka 18. Kot je bilo rečeno že prejšnjem poglavju, pazimo, da je enica te razlike (8) točno pod enico trenutnega deljenca (3). Po domače rečeno »se držimo desnega robu rumenega polja«.

Celotni deljenec je v našem primeru enak 12345, »trenutni deljenec« (v prvem koraku) pa predstavljajo njegove prve tri števke (123, v rumenem polju do »hakeljca«). Naslednja števka deljenca je tako (v prvem koraku) 4, ki prva sledi »hakeljcu«. Za lažjo predstavo ta števka leži na modri podlagi.

To števko (4) nato dodamo na desno stran razlike (18), po domače lahko rečemo, da 4 »pade dol«. Za lažjo predstavo je pot padanja obarvana modro. Ko 18 in 4 »sestavimo skupaj«, dobimo »trenutni deljenec« za naslednji korak, to je 184.

Tega nato delimo z 21 in tako naprej ...

Kdaj je podpisovanja konec?

Predpostavimo, da želimo rezultat zapisati v obliki celoštevilskega količnika in ostanka.
S postopkom, opisanim v prejšnjem koraku, nadaljujemo toliko časa, da »pade dol« še zadnja števka celotnega deljenca, s čimer dobimo naš zadnji »trenutni deljenec«. Deljenje zadnjega »trenutnega deljenca« z deliteljem nam da še zadnjo števko količnika in ostanek.

V našem primeru je celotni deljenec enak 12345, torej je njegova »zadnja števka« 5. To zapišemo desno od razlike 16, ki smo jo podpisali pod prejšnji »trenutni deljenec« 184. Naš zadnji »trenutni deljenec« je tako 165. Za količnik 165 : 21 smo ocenili vrednost 7. Ta postane zadnja števka količnika (587). Razlika med zmnožkom »množenja nazaj« (21 · 7 = 147) in »trenutnim deljencem« (165) pa je enaka 18. Ta razlika je naš ostanek, saj – po domače - »nima več kaj dol pasti«.

V primeru, da želimo rezultat zapisati v obliki decimalnega števila, za zadnjo zapisano števko delitelja zapišemo decimalno vejico in s postopkom nadaljujemo vse dokler je razlika med zmnožkom »množenja nazaj« in »trenutnim deljencem« različna od nič. To lahko traja tudi »v neskončnost«, zato je včasih potrebno na neki decimalki rezultat zaokrožiti. Več o tem postopku povem kdaj drugič. ;)

Kako vem, da je rezultat pravilen (oziroma vsaj smiseln)?

Marsikdo od nas je verjetno že kdaj na testu oddal kakšno »neumnost«, recimo rezultat za premer atoma, merjen v centimetrih. :) V izogib takim spodrsljajem je dobro izračun preveriti oziroma rezultat oceniti »na palec«, bodisi pred zapisom končnega odgovora ali pa že na začetku, da vemo, kaj pričakovati.

Pri računu deljenja to lahko storimo zelo enostavno tako, da deljenec zaokrožimo na dve, delitelj pa na eno številsko mesto (več o zaokroževanju si lahko preberete tule), okrajšamo odvečne ničle in izračunamo »kar ostane«. Zakaj zaokrožati na tak način? Zato, ker s tem dobimo preprost račun deljenja dvomestnega števila z enomestnim, katerega lahko enostavno rešimo že s poznavanjem poštevanke in nekaj »premetavanja« ničel.

V našem primeru deljenec 12345 zaokrožimo na 12000 (številska mesta štejemo od leve proti desni), delitelj pa na 20. Ker je deljenje isto kot ulomek, zadnji ničli lahko enostavno »okrajšamo« in dobimo račun 1200 : 2, katerega rezultat je 600. Račun deljenja »iz poštevanke«, ki ga moramo pri tem izračunati, je 12 : 2, kar je enako 6, ničli v deljencu pa se »preneseta« na količnik.

Računanja pri matematiki marsikdo ne mara, medtem ko je geometrija, vzorci, marsikje tudi logika in kombinatorika med bolj priljubljenimi.

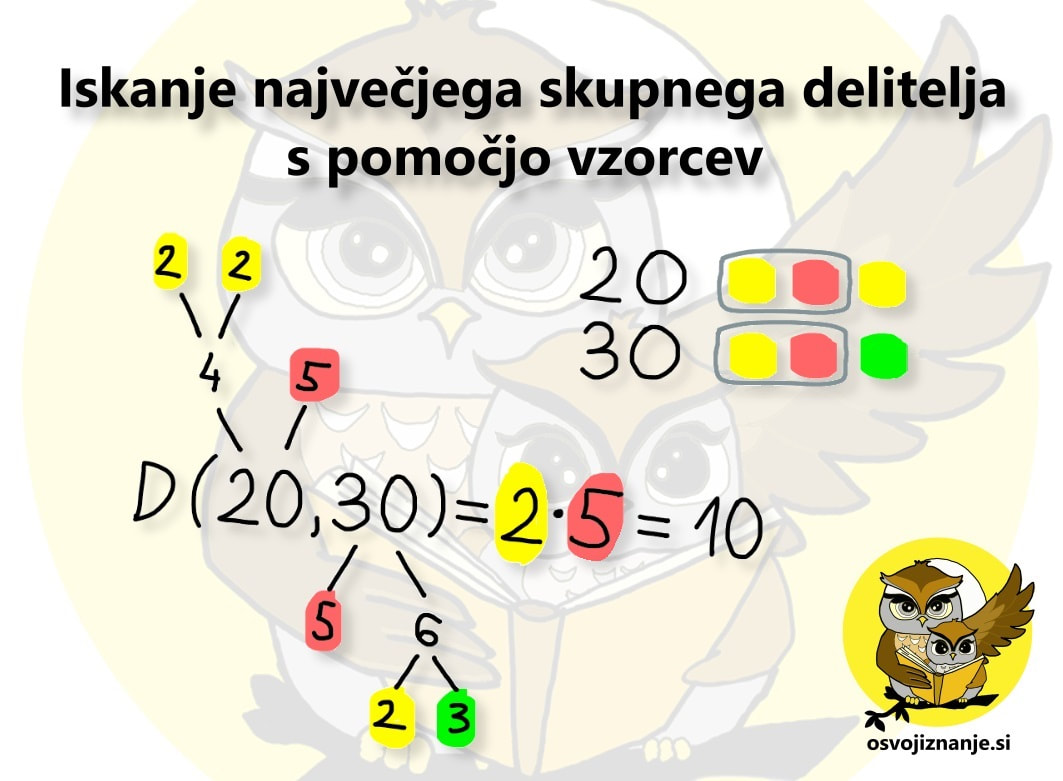
Tudi za določanje največjega skupnega delitelja (z VELIKO črko D ga označimo zato, ker je NAJVEČJI) obstaja "neračunska" metoda in sicer s pomočjo vzorcev.

Navodilo je preprosto, oglejmo si ga na primeru iskanja največjega skupnega delitelja števil 20 in 30:

1. Števili razcepimo na prafaktorje ("vizualcem" je sigurno bližje prikazana metoda z drevesno strukturo), v našem primeru 20 = 2 · 2 · 5 in 30 = 2 · 3 · 5
2. Razcepa predstavimo kot vzorca (recimo rumena pika za prafaktor 2, zelena za prafaktor 3 in rdeča za prafaktor 5)
3. Pomislimo: ker iščemo delitelj, iščemo del vzorca, ki si ga števili delita (v našem primeru oba vzorca vsebujeta eno rumeno in eno rdečo piko, medtem ko se v tretji piki razlikujeta - pri 20 je rumena, pri 30 pa zelena)
4. Zmnožimo prafaktorja, ki pripadata ujemajočem se delu vzorca (v našem primeru sta to "rumena" 2 in "rdeča" 5, kar pomeni, da je rezultat 2 · 5 = 10)

Omenjeno metodo lahko uporabimo tudi za iskanje največjega skupnega delitelja več števil.