|
Pri seštevanju in odštevanju ulomkov je potrebno najti najmanjši skupni imenovalec (pri množenju in deljenju tega ne počnemo!) Teoretični način 1 - metoda iskanja najmanjšega skupnega večkratnika Ste vedeli, da je iskanje najmanjšega skupnega imenovalca v bistvu iskanje najmanjšega skupnega večkratnika? Dejansko vidimo, da je metoda za nekaj uporabna :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/30, 1/10 in 1/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa iz zgornjih vrstic "poberimo" praštevila, ki jih bomo uporabili v končnem izračunu. Pozor! Vsako nastopajoče praštevilo vzamemo le enkrat, razen če se le-to znotraj ene vrstice ponovi! V našem primeru se v zadnji vrstici ponovi 2, zato jo vzamemo dvakrat:
Ugotovimo, da je skupni imenovalec ulomkov 1/30, 1/10 in 1/20 enak
Primer 2: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Razstavljeni imenovalci so:
Dvojka se v drugi vrstici ponovi, zato jo vzamemo dvakrat, trojko pa enkrat:
Teoretični način 2 - metoda dopolnjevanja imenovalca do najmanjšega skupnega imenovalca Ta metoda je najprimernejša za razumevanje bistva najmanjšega skupnega imenovalca. Primer 1: Poiščimo skupni imenovalec ulomkov 5/30, 1/10 in 3/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa dopolnimo imenovalce z manjkajočimi faktorji - praštevili (množenje!) tako, da bodo vsi enaki:
Pozor! Vsako število, ki ga dodamo v imenovalec, moramo dodati tudi v števec! In ne pozabimo, med števili je znak za množenje! Sedaj imamo povsod v imenovalcu 2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 60. Račun z ulomki izgleda takole: Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 3/10 in 5/15. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 120. Račun z ulomki izgleda takole: Primer 3: Poiščimo skupni imenovalec ulomkov 1/3, 3/4 in 5/6. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*3, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 12. Račun z ulomki izgleda takole: Metoda je primerna tudi za računanje z izrazi: Primer 4: Izračunajmo naslednji račun. Če imenovalec tretjega ulomka zapišemo kot zmnožek dveh dvočlenikov, imamo situacijo zelo podobno situaciji v prvih treh primerih, le da tu namesto številk množimo dvočlenike v oklepajih. Lahko bi npr. množili tudi spremenljivke (črke: a,b,x,y,...). Imenovalca tretjega ulomka torej ne bomo zapisali kot zmnožek praštevil, ampak kot zmnožek dvočlenikov v oklepajih. Za dobro voljo: v tovrstnih matematičnih nalogah sta dvočlenika, ki ju dobimo z razstavljanjem enega od imenovalcev, ravno dvočlenika iz imenovalcev preostalih dveh ulomkov, tako da je taka naloga dokaj lahko rešljiva ;) No, tako je tudi v našem primeru: Dopolnimo imenovalce z manjkajočimi faktorji (dvočleniki v oklepajih) tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu (x+2)(x-3), kar pomeni, da smo našli najmanjši skupni imenovalec, to je (x+2)(x-3). Račun z ulomki izgleda takole: Način s poskušanjem 1: množenje in postopno deljenje
Načina s poskušanjem sta primerna za tiste, ki zadevo že nekoliko bolje obvladate :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. vse imenovalce zmnožimo med seboj:
72 je vsekakor skupni imenovalec 3, 4 in 6, ne vemo pa še, če je to najmanjši skupni imenovalec. Če se nam ne ljubi posameznih imenovalcev razstavljati na praštevila, lahko poskusimo s poskušanjem :) 72 delimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je še vedno skupni imenovalec vseh 3 števil v imenovalcih:
S poskušanjem smo ugotovili, da je najmanjši skupni imenovalec ulomkov 1/3, 1/4 in 1/6 število 12. Metoda z deljenjem je primernejša za manjše vrednosti imenovalcev, če so pa te večje, pa uporabimo lahko naslednjo: Način s poskušanjem 2: postopno množenje Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Poiščimo največji imenovalec (v našem primeru je to 6) in preverimo, če je mogoče deljiv z ostalimi imenovalci (v našem primeru sta to 3 in 4). Če je deljiv, je to že kar največji skupni imenovalec. Če ni deljiv, ga postopoma množimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je novo število deljivo z vsemi imenovalci. Kot ste opazili, je tudi to metoda s poskušanjem :)
Tole je bilo pa skorajda prelahko :) Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 1/10 in 1/15. Najprej preverimo, če je največji imenovalec (v našem primeru je to 15) deljiv z 8 in 10. Ker ni deljiv, ga moramo množiti s praštevili:
Primer 3: Poiščimo skupni imenovalec ulomkov 1/2, 1/3 in 1/6. Tu je največji izmed imenovalcev že kar največji skupni imenovalec. V tem primeru nam ga ni potrebno množiti s praštevili: Največji skupni imenovalec ulomkov 1/2, 1/3 in 1/6 je 6, saj je 6 deljiva tako z 2 kot s 3.
0 Comments
Predpostavimo, da veste, kaj je veččlenik (če pa slučajno ne, si preberite tole ;) )
Razložimo na primeru: Zmnožimo:
Račun bo torej: (a + b)(c + d + e). Oklepaji so nujni! "Vsak z vsakim" v naslovu pomeni, da moramo pri množenju veččlenikov vsak člen prvega veččlenika pomnožiti z vsakim členom drugega veččlenika. Pozor! členov znotraj oklepaja ne množimo med seboj! Z drugimi besedami povedano, vsak člen iz levega oklepaja bo enkrat stal zraven vsakega člena iz desnega oklepaja: (a + b)(c + d + e) = ac + ad + ae + bc + bd + be Ni panike, kvadrat zapiši kot produkt dvočlenika samega s seboj:
(x-3)² je isto kot (x-3)(x-3). Sedaj pa samo uporabite pravilo za množenje dvočlenikov (saj poznate tisto, "zmnoži vsakega z vsakim"?). Za zgornji primer dobimo x²-3x-3x+9. Izraz uredimo in dobimo: (x-3)² = x²-6x+9. Na enak način si lahko pomagamo tudi s kubom dvočlenika, s tem da problem rešujemo po korakih: (x-3)³ je isto kot (x-3)(x-3)(x-3) Med seboj najprej zmnožimo prva dva oklepaja, nato pa še tretjega: (x-3)(x-3)(x-3) = (x²-3x-3x+9)(x-3) =... Ni panike, uporabi Vietovo pravilo, pri čemer upoštevaš, da je linearni koeficient enak nič:
x²-9 je isto kot x²+0x+9. Ker je linearni koeficient enak 0, je potrebno prosti člen (9 v zgornjem izrazu) predstaviti kot zmnožek dveh nasprotno enakih števil (+√9 in - √9 oz. +3 in -3 v zgornjem izrazu). Velja torej: x²-9 = (x+3)(x-3). V nadaljevanju sledi razlaga za razstavljanje izrazov po Vietovem pravilu. Postopek je uporaben za "lažjo obliko" izraza, pri čemer predpostavimo:
Razložimo zgornji izraz:
Sedaj pa navodilo. Aha, preden se lotimo reševanja, povejmo še, kaj pričakujemo za rešitev :) Ker je spremenljivka v zgornjem izrazu x, bo rešitev v obliki (x±a)(x±b). X je seveda spremenljivka, a in b pa bomo določili z naslednjim postopkom:
Preprosto :) in sicer v dveh korakih:
Nekaj primerov:
To najlažje naredimo tako, da delimo števec z imenovalcem, saj ulomek v matematiki pomeni deljenje. Število s končnim decimalnim zapisom (po domače tako decimalno število, ki se ne "vleče" v neskončnost) pa dobimo samo, če ulomek razširimo tako, da v imenovalcu dobimo potenco števila 10 (po domače števila, ki ima spredaj 1, zadaj pa same ničle, npr. 10, 100, 1000,...) V število s končnim decimalnim zapisom lahko pretvorimo ulomek, ki ima v imenovalcu:
V število s končnim decimalnim zapisom pa ne moremo pretvoriti ulomkov, ki imajo v imenovalcu:
Pozor! če imenovalec množimo z nekim številom, moramo seveda z istim številom pomnožiti tudi števec, sicer bomo v godlji! :) Sedaj, ko imamo desetiški ulomek (v imenovalcu je potenca števila 10), le še:
Nekaj primerov:
V nadaljevanju sledi nekaj nasvetov za reševanje nalog v stilu: "Zapiši množico točk, ki je predstavljena v koordinatnem sistemu..." Saj veste, ko imate na x/y "križkražu" polne in črtkane črte, pobarvano polje pa sega v neskončnost ali pa je stisnjeno v "sendvič"... :)
1. Na sliki je samo črta
2. Na sliki je črta, od katere se levo, desno, dol ali gor proti neskočnosti razteza pobarvano polje
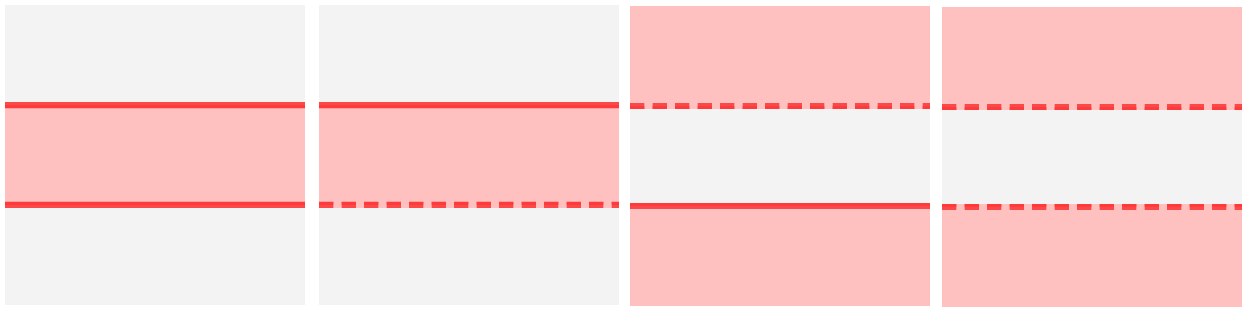
3. Na sliki sta dve vzporedni črti, med katerima se razteza pobarvano polje (ujeto v "sendvič")
Oglejte si še legendo. Saj poznate tiste naloge v stilu: "V koordinatnem sistemu nariši množico točk, ki ustreza zapisu..." In potem rišemo polne in črtkane črte, barvamo v neskončnost ali pa narišemo "sendvič"... :) Da se boste s takimi nalogami lažje spopadli, naj vam predlagamo naslednji "kuharski recept". 1a. Preverimo, ali pogoj velja za x os ali za y os (če je pogoj dvojni, preskočimo na točko 1b.) Tu bomo narisali eno vodoravno ali navpično črto.
1b. Preverimo, ali za x os ali za y os velja dvojni pogoj Tu bomo narisali dve vodoravni črti, dve navpični črti ali eno vodoravno in eno navpično črto.
2a. Preverimo, za kakšen pogoj gre [>, <, ≥, ≤ ali =] (pri pogoju za x in y preskočimo na točko 2b): Tu barvamo levo/desno oziroma gor/dol od črte iz točke 1. Pri pogoju "=" ne barvamo ničesar. Če sta pogoja za x oziroma y dva, barvamo področje med črtama ali pa področje od črt navzven.
Tu barvamo levo/desno oziroma gor/dol od črt iz točke 1b (razen pri pogoju "=", kjer ne barvamo). Obarvani področji se prekrivata, kot rešitev pa velja naslednje:
Legenda:
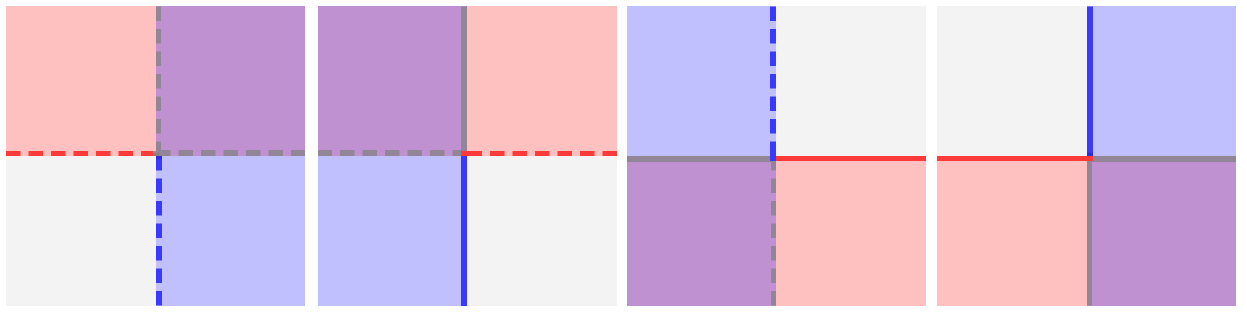
Primeri slik za enojni pogoj za x (≤, <, =, >, ≥): Primeri slik za enojni pogoj za y (≤, <, =, >, ≥): Primeri slik za za dvojni pogoj za x: Primeri slik za dvojni pogoj za y: Primeri slik za pogoj za x in y (logični operator "in"): Primeri slik za pogoj za x in y (logični operator "ali"):
|
ARHIV
May 2024
KATEGORIJE
All
|
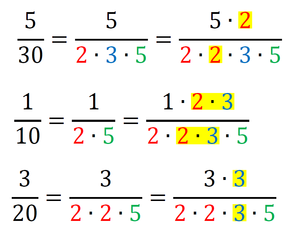
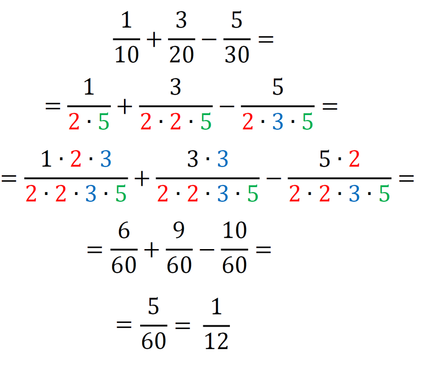
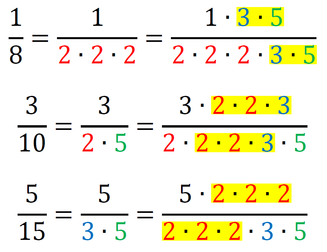
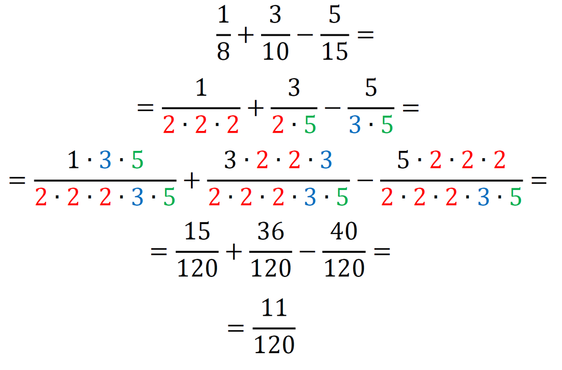
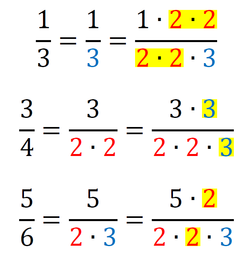
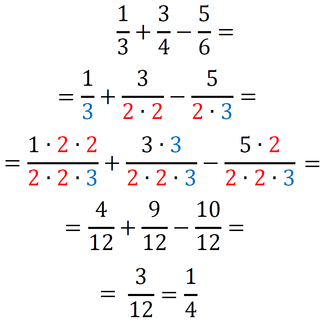
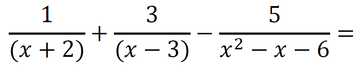
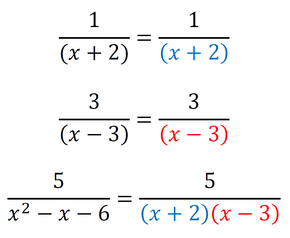
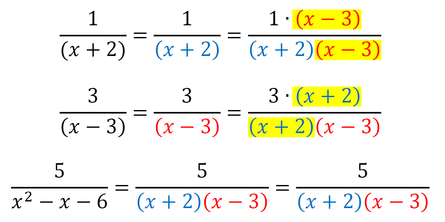
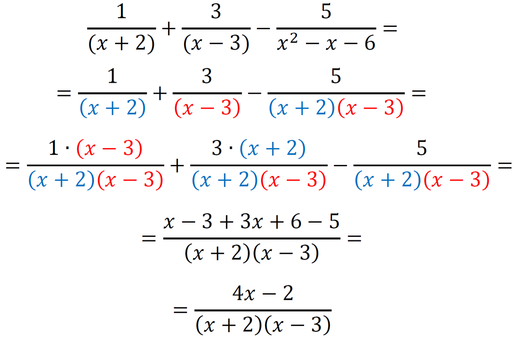
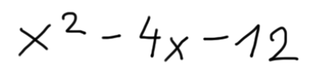
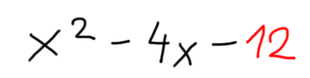
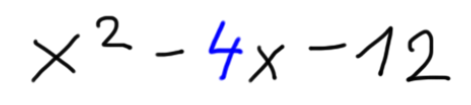
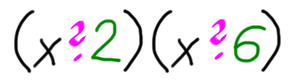
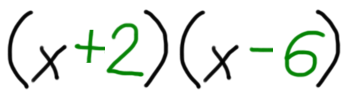




 RSS Feed
RSS Feed
