|
Pri seštevanju in odštevanju ulomkov je potrebno najti najmanjši skupni imenovalec (pri množenju in deljenju tega ne počnemo!) Teoretični način 1 - metoda iskanja najmanjšega skupnega večkratnika Ste vedeli, da je iskanje najmanjšega skupnega imenovalca v bistvu iskanje najmanjšega skupnega večkratnika? Dejansko vidimo, da je metoda za nekaj uporabna :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/30, 1/10 in 1/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa iz zgornjih vrstic "poberimo" praštevila, ki jih bomo uporabili v končnem izračunu. Pozor! Vsako nastopajoče praštevilo vzamemo le enkrat, razen če se le-to znotraj ene vrstice ponovi! V našem primeru se v zadnji vrstici ponovi 2, zato jo vzamemo dvakrat:
Ugotovimo, da je skupni imenovalec ulomkov 1/30, 1/10 in 1/20 enak
Primer 2: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Razstavljeni imenovalci so:
Dvojka se v drugi vrstici ponovi, zato jo vzamemo dvakrat, trojko pa enkrat:
Teoretični način 2 - metoda dopolnjevanja imenovalca do najmanjšega skupnega imenovalca Ta metoda je najprimernejša za razumevanje bistva najmanjšega skupnega imenovalca. Primer 1: Poiščimo skupni imenovalec ulomkov 5/30, 1/10 in 3/20. Najprej zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Sedaj pa dopolnimo imenovalce z manjkajočimi faktorji - praštevili (množenje!) tako, da bodo vsi enaki:
Pozor! Vsako število, ki ga dodamo v imenovalec, moramo dodati tudi v števec! In ne pozabimo, med števili je znak za množenje! Sedaj imamo povsod v imenovalcu 2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 60. Račun z ulomki izgleda takole: Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 3/10 in 5/15. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*2*3*5, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 120. Račun z ulomki izgleda takole: Primer 3: Poiščimo skupni imenovalec ulomkov 1/3, 3/4 in 5/6. Zapišimo vse tri imenovalce kot zmnožek praštevil (2, 3, 5, 7, 11,...):
Dopolnimo imenovalce z manjkajočimi faktorji - praštevili tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu 2*2*3, kar pomeni, da smo našli najmanjši skupni imenovalec, to je 12. Račun z ulomki izgleda takole: Metoda je primerna tudi za računanje z izrazi: Primer 4: Izračunajmo naslednji račun. Če imenovalec tretjega ulomka zapišemo kot zmnožek dveh dvočlenikov, imamo situacijo zelo podobno situaciji v prvih treh primerih, le da tu namesto številk množimo dvočlenike v oklepajih. Lahko bi npr. množili tudi spremenljivke (črke: a,b,x,y,...). Imenovalca tretjega ulomka torej ne bomo zapisali kot zmnožek praštevil, ampak kot zmnožek dvočlenikov v oklepajih. Za dobro voljo: v tovrstnih matematičnih nalogah sta dvočlenika, ki ju dobimo z razstavljanjem enega od imenovalcev, ravno dvočlenika iz imenovalcev preostalih dveh ulomkov, tako da je taka naloga dokaj lahko rešljiva ;) No, tako je tudi v našem primeru: Dopolnimo imenovalce z manjkajočimi faktorji (dvočleniki v oklepajih) tako, da bodo vsi enaki:
Sedaj imamo povsod v imenovalcu (x+2)(x-3), kar pomeni, da smo našli najmanjši skupni imenovalec, to je (x+2)(x-3). Račun z ulomki izgleda takole: Način s poskušanjem 1: množenje in postopno deljenje
Načina s poskušanjem sta primerna za tiste, ki zadevo že nekoliko bolje obvladate :) Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. vse imenovalce zmnožimo med seboj:
72 je vsekakor skupni imenovalec 3, 4 in 6, ne vemo pa še, če je to najmanjši skupni imenovalec. Če se nam ne ljubi posameznih imenovalcev razstavljati na praštevila, lahko poskusimo s poskušanjem :) 72 delimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je še vedno skupni imenovalec vseh 3 števil v imenovalcih:
S poskušanjem smo ugotovili, da je najmanjši skupni imenovalec ulomkov 1/3, 1/4 in 1/6 število 12. Metoda z deljenjem je primernejša za manjše vrednosti imenovalcev, če so pa te večje, pa uporabimo lahko naslednjo: Način s poskušanjem 2: postopno množenje Primer 1: Poiščimo skupni imenovalec ulomkov 1/3, 1/4 in 1/6. Poiščimo največji imenovalec (v našem primeru je to 6) in preverimo, če je mogoče deljiv z ostalimi imenovalci (v našem primeru sta to 3 in 4). Če je deljiv, je to že kar največji skupni imenovalec. Če ni deljiv, ga postopoma množimo z različnimi praštevili (začnemo z 2 in 3, mogoče 5) in sproti preverjamo, če je novo število deljivo z vsemi imenovalci. Kot ste opazili, je tudi to metoda s poskušanjem :)
Tole je bilo pa skorajda prelahko :) Primer 2: Poiščimo skupni imenovalec ulomkov 1/8, 1/10 in 1/15. Najprej preverimo, če je največji imenovalec (v našem primeru je to 15) deljiv z 8 in 10. Ker ni deljiv, ga moramo množiti s praštevili:
Primer 3: Poiščimo skupni imenovalec ulomkov 1/2, 1/3 in 1/6. Tu je največji izmed imenovalcev že kar največji skupni imenovalec. V tem primeru nam ga ni potrebno množiti s praštevili: Največji skupni imenovalec ulomkov 1/2, 1/3 in 1/6 je 6, saj je 6 deljiva tako z 2 kot s 3.
0 Comments
Leave a Reply. |
ARHIV
May 2024
KATEGORIJE
All
|
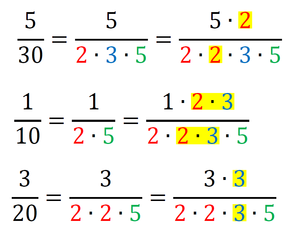
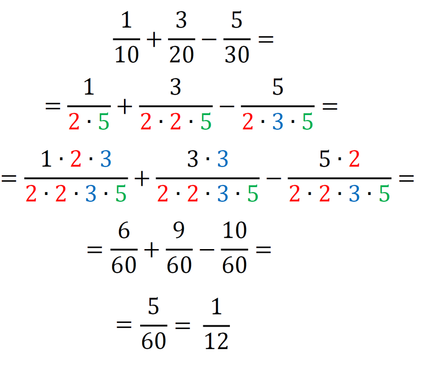
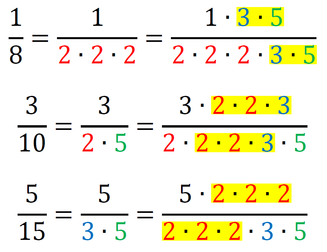
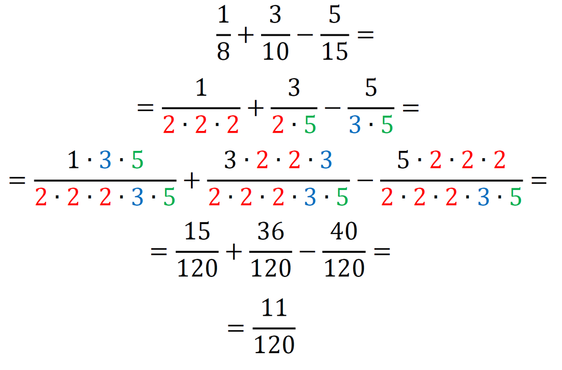
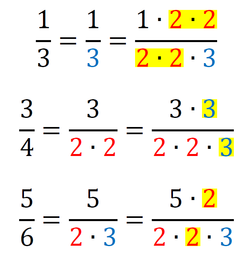
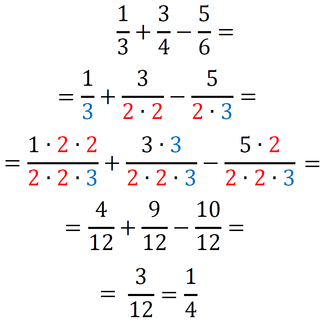
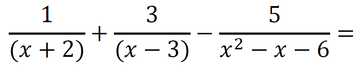
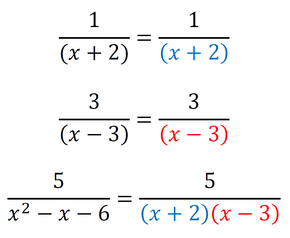
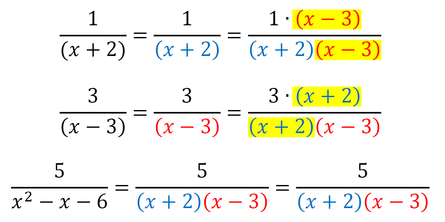
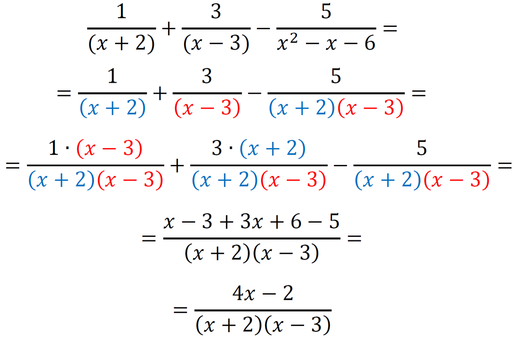
 RSS Feed
RSS Feed
