|
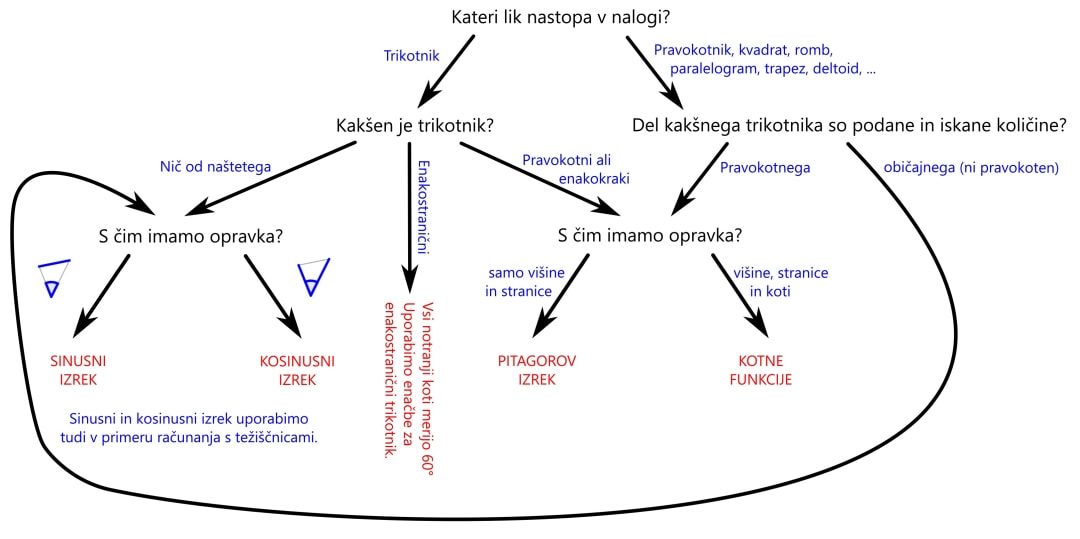
Marsikdo se pri nalogah z razreševanjem trikotnika znajde pred vprašanjem, kateri izrek uporabiti. Je to nemara sinusni, kosinusni, morda Pitagorov? Ali pa le kotne funkcije. Da se boste v tovrstnih situacijah lažje znašli, smo vam pripravili naslednji algoritem: Nekaj navodil za tolmačenje algoritma:
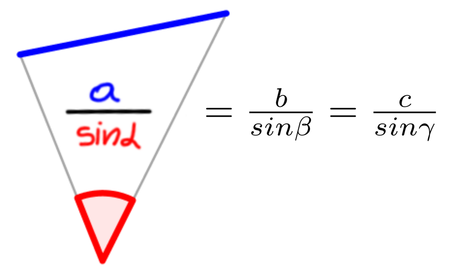
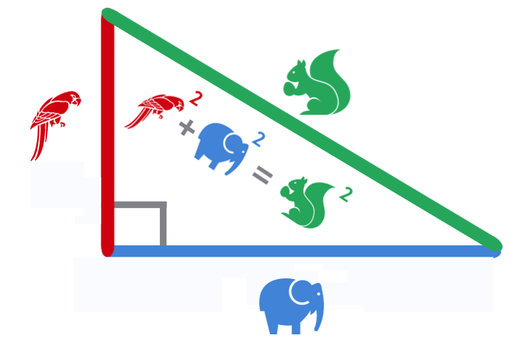
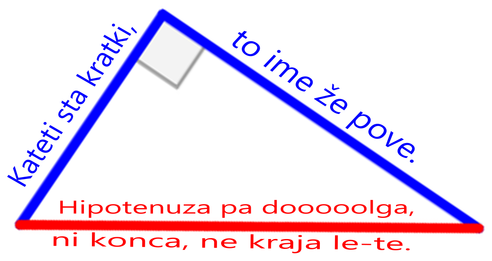
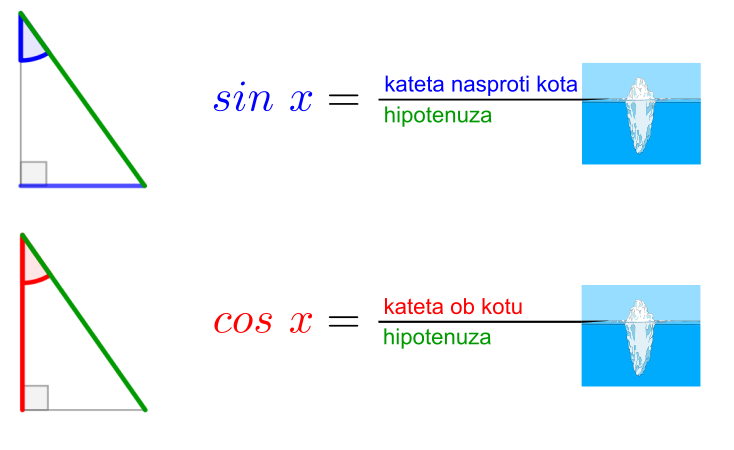
Sinusni izrek si lahko zapomnimo grafično ... ... ali pa s pomočjo verza: Če kot in stranica stojita SI Nasproti, trikotnika s SINusnim izrekom se loti! Tudi kosinusni izrek si lažje zapomnimo, če si ga narišemo ... ... ko pa nas misli popeljejo v naravo, si lahko barvno pudarjen del predstavljamo kot KOSov kljun :) Pitagorov izrek ni nič drugega kot posebna oblika kosinusnega izreka, ko je kot med stranicama na zgornji sliki enak 90° in obarvani del enačbe "pade", saj je cos 90° enak 0. Pomembno! Enačb se ne učite na stranico in kot določeno! Stranice so lahko označene z a, b in c, predstavljamo pa si jih praktično lahko kot karkoli ... recimo kot živali :) Kotnih funkcij se nam ni potrebno učiti vseh "na pamet". Preden povemo, kako to doseči, ponovimo razliko med katetami in hipotenuzo (to so stranice v pravokotnem trikotniku, če kdo slučajno še ne ve): Kateti sta kratki, to ime že pove. Hipotenuza pa dooooolga, ni konca, ne kraja le-te. Kotne funkcije so štiri (sinus, kosinus, tangens in kotangens), a "na pamet" se moramo naučiti le enačbi za prvi dve ... Če kot in kateta stojita SI Nasproti, SINus vržem v račun, ko pa hodita po isti poti, kosinus na to ne bo imun. Sinus in kosinus, kje je tu fora? Enačbi zanju sta kot ledena gora. Stranica krajša gor' in daljša dol', Ne en ne drug večji od 1 ne bo nikol'. ... medtem ko preostali dve kotni funkciji (tangens in kotangens) enostavno izpeljemo...ali pa kar zapojemo: 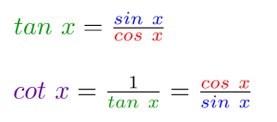 Enačbi za sinus in kosinus se naučim, za tangens pa kar prvega z drugim delim. Če pa kotangens koga zanima še, naj tangens na glavo obrne le.
0 Comments
Leave a Reply. |
ARHIV
May 2024
KATEGORIJE
All
|
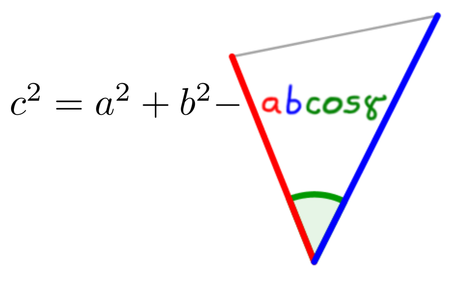
 RSS Feed
RSS Feed
