|
"Kakšno pravilo pa je že spet to?" boste nemara pripomnili. Brez panike, to pravilo ni le še ena kaplja v morju pravil, med katerimi se ne znajdete več. Da bi vam olajšali pot iz matematične zagate, smo za vas pripravili nekaj temeljnih pravil za računanje. In jih poimenovali kar po barvah, česar boste veseli predvsem "vizualni tipi". Vsako izmed pravil bomo predstavili posebej, potem pa se bomo nanje po potrebi sklicevali. Videli boste, da teh pravil niti ni toliko, kot si mislimo. Vsaj ne osnovnih. Kar nakazuje, da matematika res ni tako težka, kot se zdi na prvi pogled :) Začnimo z najosnovnejšim pravilom računanja, pravilom o seštevanju in odštevanju. Pravilo seštevanja in odštevanja uporabimo pri:
Pravilo se glasi:
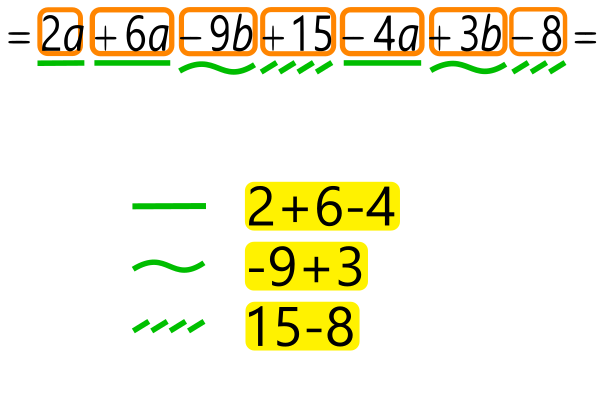
Pri računanju si lahko pomagamo tudi s tabelo. Pozor! V algebri (številke in črke) podobne člene seštevamo / odštevamo ločeno, saj "hrušk in jabolk" seveda ne moremo seštevati :). Ideja (aritmetika - samo številke): Števila, na katerih bomo uporabili rumeno pravilo, lahko obkrožimo z rumeno in jih pobarvamo. Primeri uporabe rumenega pravila v aritmetičnem računskem izrazu Ideja (algebra - številke in črke): Na koncu računa, ko imamo le še "kačo" členov, vsak člen obkrožimo z oranžno barvo, pod členi pa z zeleno barvo označimo posamezne podobne člene (ravna črta, vijugasta črta, poševno črtkana črta, ...) Tako dobimo pregleden "zemljevid" podobnih členov, ki nam bo olajšal končen izračun po rumenem pravilu z upoštevanjem grupiranja podobnih členov (zeleno pravilo). Primer končne "kače" členov; členi so obkroženi z oranžno barvo in nato grupirani po zelenem pravilu. Znotraj vsake "zelene" skupine je uporabljeno rumeno pravilo; ravna črta so a-ji, vijugasta b-ji, poševno črtkana črta pa predstavlja številske člene.
0 Comments
Lepota matematike je (med drugim) tudi v tem, da se je marsikaj potrebno naučiti samo na pol12/8/2018 V matematiki najdemo veliko računskih operacij, ki so med seboj obratne. To pomeni, da rezultat prve operacije z drugo operacijo vrnemo nazaj v začetno stanje. Vsakdo od vas bi si verjetno želel matematične operacije, ki bi vašo razmetano sobo pospravila nazaj v "pospravljeno stanje" ;)
"In kje je sedaj tisti del, ki pravi, da se je potrebno naučiti samo na pol?" boste dejali. Če sta računski operaciji obratni, je dovolj, da se določenega postopka naučimo le za prvo, za drugo pa vemo, da omenjeni postopek "obrne na glavo". Oglejmo si primer. Množenje in deljenje sta obratni računski operaciji. Če vemo, da vsako množenje z 10 rezultatu doda ničlo (oziroma decimalno mesto premakne v desno), jo bo vsako deljenje z 10 odvzelo (oziroma decimalno mesto premaknilo v levo). Naštejmo nekaj najbolj pogosto uporabljanih računskih operacij, ki so med seboj obratne:
Oglejmo si še en primer za potenciranje in korenjenje, konkretno za kvadrat in kvadratni koren:
Včasih dve obratni računski operaciji najdemo kar v enem računu, česar se še posebej razveselimo, saj ena operacija izniči drugo, tako da nam sploh ni potrebno ničesar računati :) Oglejmo si nekaj primerov:
Ste vedeli, da se je tudi poštevanke dovolj naučiti le na pol? Za to pa ima zaslugo zakon o zamenjavi, ki velja za množenje. 3·4 je tako enako 4·3 in tako naprej ... Zakon o zamenjavi velja tudi za seštevanje. Ste se pri iskanju ničel polinoma kdaj spraševali, zakaj ima ničla vedno nasprotni predznak od predznaka, ki se pojavi v oklepaju razstavljenega polinoma?
Če ste se, je to dober znak, saj želite razumeti, kaj počnete in to je pri matematiki ključnega pomena. Za primer vzemimo polinom: f(x)=x²-x-6 Ko ga razstavimo, dobimo: f(x)=(x-3)(x+2) Ničlo poiščemo tako, da polinom izenačimo z 0: (x-3)(x+2)=0 Da bo zmnožek oklepajev enak 0, mora biti vrednost vsaj enega oklepaja enaka 0, torej:
Če želimo, da bo x-3 enak 0, mora biti vrednost x enaka 3, saj je 3-3 enako 0. K -3 moramo torej postaviti njegovo nasprotno vrednost, da bosta skupaj enaka 0. Na enak način moramo za zagotovitev rezultata x+2=0 k +2 postaviti njeno nasprotno vrednost -2, da bosta skupaj enaka 0. Rešitvi enačbe (in hkrati ničli polinoma) sta torej
Zato, da namesto s štirimi osnovnimi računskimi operacijami (seštevanje, odštevanje, množenje in deljenje) računamo le z dvema (seštevanje in množenje).
Kako? Preprosto:
Zgornja razlaga je mogoče res nekoliko karikirana, je pa res, da omenjeni dve zakonitosti redno uporabljamo. Naj omenimo le nekaj primerov:
Za tovrstno telovadbo potrebujemo le nekaj znanja poštevanke in...dovolj veliko sobo (če boste delali majhne korake, bo šlo pa tudi v manjši sobi:)).
In kako poteka tale mešanica možganske in mišične telovadbe? Preverimo kar na primeru. Razstavimo izraz x² - 5x -36. Preden se lotimo reševanja, si pripravimo še "teren". Poštevanko verjetno še znamo (če ne, pa hitro malo ponavljat' ;) ), v sobi moramo pa označiti "točko nič", ki bo predstavljala število 0. V eno smer od te točke bodo koraki naprej oziroma "v plus", v drugo pa koraki nazaj oziroma "v minus". Začnimo s številom 36. Pomislimo na vse rezultate poštevanke, ki znašajo 36. Naloga je nekoliko zahtevnejša od "klasične", saj jo opravljamo v obratni smeri. 36 vemo, da je enako:
Dobili smo pet kombinacij množenca in množitelja. Vsak tak par (na primer 3 in 12, 4 in 9,...) nam predstavlja število korakov. Naša naloga je, da ugotovimo, s katerim parom korakov lahko pridemo do koeficienta linearnega člena. V našem primeru je to -5, torej moramo biti na koncu sprehoda 5 korakov "v minusu". Začnemo pa vedno na "točki nič". Pri tej nalogi je pomembno tudi to, kakšen je predznak pri številskem členu:
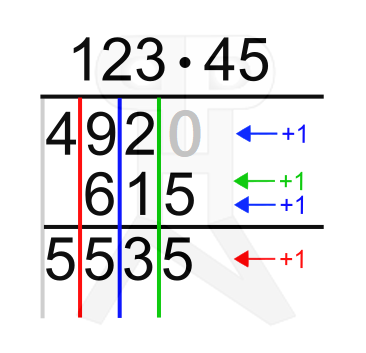
V našem primeru je številski člen negativen (-36), zato bomo korake delali "mal' naprej in mal' nazaj" (ali pa obratno, po želji :)) Po kombinaciji možganske in mišične telovadbe ugotovimo, da do 5 korakov "v minus" pridemo lahko tako, da naredimo 4 korake naprej in 9 korakov nazaj (lahko tudi najprej 9 korakov nazaj in nato 4 korake naprej). Za rešitev smo uporabili torej četrti par števil (oziroma korakov) iz zgornjega seznama, 4 in 9. Rešitev se torej glasi: x² - 5x -36 = (x+4)(x-9) saj smo do cilja prišli tako, da smo naredili 4 korake naprej in 9 korakov nazaj. V šoli že leta učijo vedno eno in isto metodo za množenje. Največji argument za to je nevarnost, da bi se učenci ob različnih metodah preveč zbegali in potem vse pomešali. Delno je to res, saj se v šoli ponavadi učimo postopkov in dva postopka za isto stvar bi nas res lahko zmedla. Po drugi strani pa se določeno snov lahko bolje naučimo, če jo pogledamo iz več zornih kotov. Ne nazadnje se tudi pri vsakem nakupu (npr. mobilnega telefona), kjer imamo "v igri več favoritov", o vsakem izmed njih poučimo mnogo bolje, kot pa da bi kupili prvi telefon, ki nam "pride pod roke". Zato smo vam pripravili primerjavo treh najbolj uporabljanih metod za množenje dveh večmestnih števil ter navedli njihove glavne prednosti in slabosti. Prvo metodo smo poimenovali "klasična", to verjetno vsi poznamo iz šole. Druga je "metoda z mrežo", ki je aktualna predvsem na angleško govorečem področju (zanimiva za tiste, ki radi naročate knjige iz tujine). Tretja metoda pa je "japonska" in bo všeč predvsem tistim, ki radi rišete. Vse tri metode bodo predstavljene skozi primer množenja števil 123 in 45. Klasična metoda Postopek:
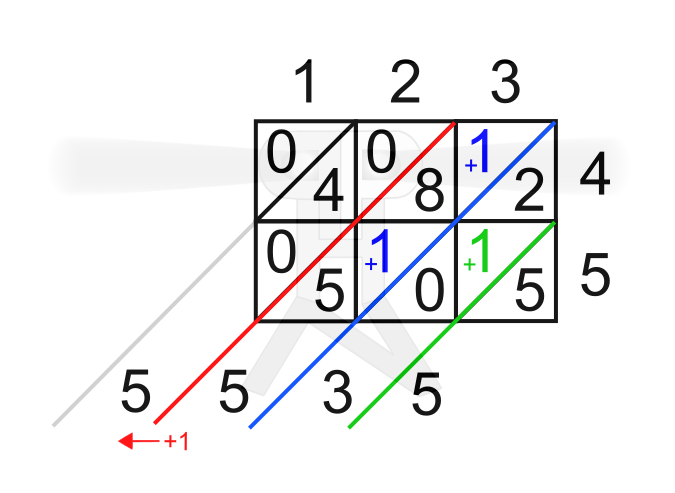
Prenos naprej: Prvič (po potrebi) prenašamo vrednost desetice naprej oz. levo pri množenju (v našem primeru je npr. pri množenju števk 3 in 4 rezultat 12, kjer zapišemo enico (2), desetico (1) pa prenesemo naprej), nato pa (po potrebi) še pri seštevanju zmnožkov (v našem primeru je npr. pri seštevanju 9 in 6 rezultat 15, kjer zapišemo enico (5), desetico (1) pa prenesemo naprej). Prednosti: Zasede najmanj prostora, večja preglednost. Slabosti: Množenje večmestnega števila z enomestnim (pri metodi z mrežo in japonskem načinu vedno množimo samo enomestna števila), nepregledno zapisovanje prenosa naprej (pri metodi z mrežo sta "moder" in "zelen" prenos naprej zapisana na točno določenem mestu v tabeli, pri klasičnem pa običajno med velike cifre vrivamo majhne enice, ki nas spomnijo, da moramo narediti prenos naprej). Metoda z mrežo Postopek:
Prenos naprej: Prenos naprej pri množenju ni potreben, po potrebi vrednost desetice prenesemo naprej pri seštevanju zmnožkov. V našem primeru je npr. pri seštevanju 5, 1, 8 in 1 rezultat 15, kjer zapišemo enico (5), desetico (1) pa prenesemo naprej. Prednosti: Prenos naprej pri množenju ni potreben. Slabosti: Potrebno je dorisati prečne črte med enicami/deseticami/stoticami/..., potrebno je paziti, da števila pravilno vnesemo v tabelo (od leve proti desni in od zgoraj navzdol). Japonska metoda Postopek:
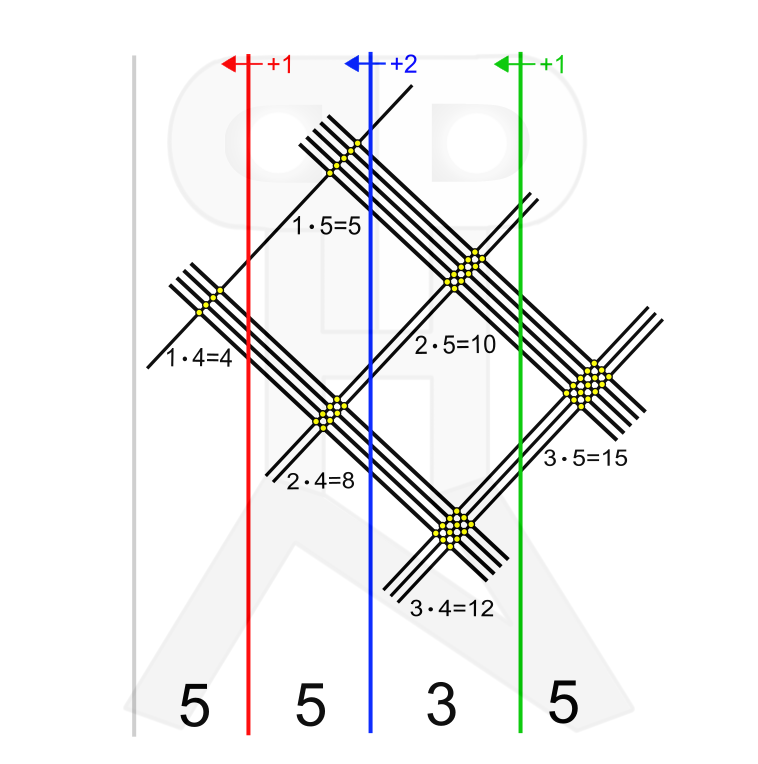
Prenos naprej: Prenos naprej se izvaja samo v končnem koraku, ko seštevek točk v posameznem "stolpcu" zapisujemo na dno "stolpca". V našem primeru je npr. pri seštevanju 2•5=10, 3•4=12 in prenešene 1 rezultat 23, kjer zapišemo enico (3), desetico (2) pa prenesemo naprej. Prednosti: Vizualna metoda, motivacija za učenje poštevanke (z znanjem poštevanke lahko hitreje računamo). Slabosti: Potrebno je pravilno narisati črte (tako tiste za števke kot ločne črte med enicami/deseticami/stoticami...), zasede veliko prostora, dolgotrajno štetje točk (če ne znamo poštevanke). Opisali smo tri metode, nedvomno pa jih obstaja še več. Zanimiv način množenja dveh večmestnih števil je tudi uporaba zakona o distributivnosti množenja, o katerem si lahko več preberete tule. Množenje z distributivnostnim zakonom je uporabno za števila, ki se na številski osi nahajajo blizu "okroglih" vrednosti, na primer 98 in 103, ki sta blizu vrednosti 100: 98•103 = (100-2)(100+3) = 10000 + 300 - 200 - 6 = 10094 Distributivnost oziroma zakon o razčlenjevanju je lastnost množenja, da se lahko faktorji razčlenijo in posamezni členi teh faktorjev množijo. Verjetno vam je zgornji stavek popolnoma jasen. Ne? Itak :) Razložimo pojem bolj “po domače”. Verjetno vas je večina že videla kakšen napovednik za prihajajoči film. Na koncu napovednika je običajno omenjen tudi distributer (npr. “Distribucija Karantanija Cinemas”). In kaj počne distributer? Distribuira filme, seveda :) No, da se ne boste izgubili med tujkami, najprej razložimo, kaj ta beseda sploh pomeni. Po SSKJ distribucija pomeni razdeljevanje oz. razpošiljanje. Distributerji pa razdeljujejo, razpošiljajo… Filmski distributer razpošilja filme kinooperaterjem, obstajajo pa tudi drugi distributerji, recimo distributer plina, električne energije, bencina, prehrambenih izdelkov itd. In kakšno zvezo ima filmska industrija z matematiko? Če ne drugega, oboji poznajo pojem distributivnost :) Če distributer distribuira, je distributivnost sama sposobnost distribucije. Joj, kakšen stavek! :) Preden vse skupaj do konca zavozlamo, si poglejmo praktičen primer. Zamislimo si, da ima filmski distributer na mizi en kup filmskih kolutov, ki jih mora razposlati različnim kino operaterjem: Najprej jih podolgem in počez razdeli (glej črte na spodnji sliki), nato pa razpošlje. Nekaj v Kolosej, nekaj v Cineplex in tako naprej. Vsak kinooperater ima svojo barvo kolutov: In kje je tu distributivnost? Oglejmo si primer še z matematične plati.
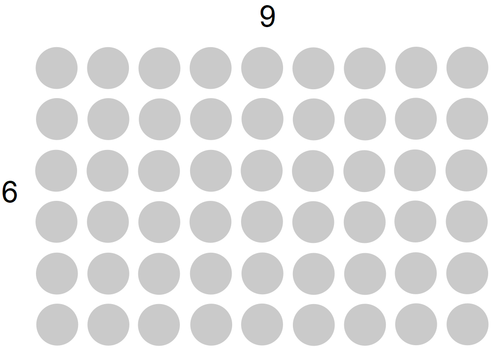
Iz prve slike s pomočjo znanja poštevanke hitro ugotovimo, da je kolutov 9•6, torej 54. Na drugi sliki pa so naslednji koluti:
Ker gre za iste kolute kot na prvi sliki, bi po logiki tudi teh moralo biti 54. S preprostim seštevanjem različnih barv ugotovimo, da naša trditev drži: 2 + 3 + 4 + 10 + 15 + 20 = 54 Vse lepo in prav, ampak še vedno ne vemo, kje je tu distributivnost. No, sedaj pa si že res zaslužite odgovor :) V računu za prvo sliko (sivi koluti) imamo dva faktorja: 9 in 6. Ker je množenje distributivno, lahko katerega koli od faktorjev razčlenimo na poljubno število členov (pretiravat pa vseeno ni treba). Mi smo razčlenili kar oba faktorja (glej drugo sliko):
Račun 9•6 je tako postal (2+3+4)(1+5). Distributivnost oziroma zakon o razčlenjevanju nadalje pravi, da je sedaj potrebno posamezne člene zmnožiti med seboj. Saj poznate tisto: “Množimo vsakega z vsakim!” Naš račun se tako glasi: 9•6 = (2+3+4)(1+5) = 1•2 + 1•3 + 1•4 + 5•2 + 5•3 + 5•4 = 2 + 3 + 4 + 10 + 15 + 20 = 54 Mogoče se tole komu zdi brez veze, češ kaj pa kompliciramo, saj bi z znanjem osnovnošolske poštevanke enostavno zmnožili 9 in 6 ter dobili rezultat 54. V bistvu ni brez veze, le primer je nekoliko prelahek. Ampak saj primeri morajo biti lahki, da jih razumemo. Poglejmo si še en primer. Zmnožimo števili 15 in 18. Tega se pa niste učili v osnovni šoli, ane? :) S pomočjo distributivnosti račun 15•18 lahko preoblikujemo na raven osnovnošolske poštevanke, začinjene z nekaj seštevanja: 15•18 = (10+5)(10+8) = 10•10 + 10•8 + 5•10 + 5•8 = 100 + 80 + 50 + 40 = 270 Pa ne recite: "Ah, sej 'mamo kalkulator!" Možgančke je fino malo peljati na sprehod, da se ne zasedijo ;) Predpostavimo, da veste, kaj je veččlenik (če pa slučajno ne, si preberite tole ;) )
Razložimo na primeru: Zmnožimo:
Račun bo torej: (a + b)(c + d + e). Oklepaji so nujni! "Vsak z vsakim" v naslovu pomeni, da moramo pri množenju veččlenikov vsak člen prvega veččlenika pomnožiti z vsakim členom drugega veččlenika. Pozor! členov znotraj oklepaja ne množimo med seboj! Z drugimi besedami povedano, vsak člen iz levega oklepaja bo enkrat stal zraven vsakega člena iz desnega oklepaja: (a + b)(c + d + e) = ac + ad + ae + bc + bd + be Kot vemo, imajo končen decimalni zapis desetiški ulomki.
In kako vemo, da je nek ulomek desetiški? Enostavno, z razcepom imenovalca na prafaktorje:
Če so med prafaktorji v imenovalcu le dvojke in/ali petice, poiščemo pare (2*5=10):
Jih znate našteti? ;) Še enkrat jih ponovimo posebej za vas:
Eksplicitna oblika zapisa enačbe premice Najprej razrešimo dilemo med eksplicitnim in implicitnim zapisom. Besedi seveda izvirata iz latinščine, v oči oziroma ušesa pa nas najbolj zbode predpona pri prvi, to je "eks-", ki po latinsko pomeni "izven" oziroma "iz". Kdo je v tem primeru "zunaj"? Odvisna spremenljivka y. Na drugo stran enačaja jo je namreč postavila neodvisna spremenljivka x v družbi koeficientov (številk). To je nekako tako, kot da bi "eks" dekle pred vrata postavilo "eks" fanta. Auč, not good. Na sliki imate primer eksplicitnega zapisa: Implicitna oblika zapisa enačbe premice Če je pri eksplicitnem zapisu odvisna spremenljivka y osamljena, ločena od neodvisne spremenljivke x in številskih koeficientov, je pri implicitnem zapisu le-ta "v dobri družbi". Na drugi strani enačbe pa je ničla, po čemer tak zapis linearne funkcije tudi najlažje prepoznamo. Če še malo "pokukamo" k latinščini, beseda eksplicitno izhaja iz latinskega izraza "implicitus", ki pomeni "vključiti, prepletati" - logično, spet je govora o odvisni spremenljivki y, ki tokrat ni osamljena (juhu :)) Odsekovna oblika zapisa enačbe premice
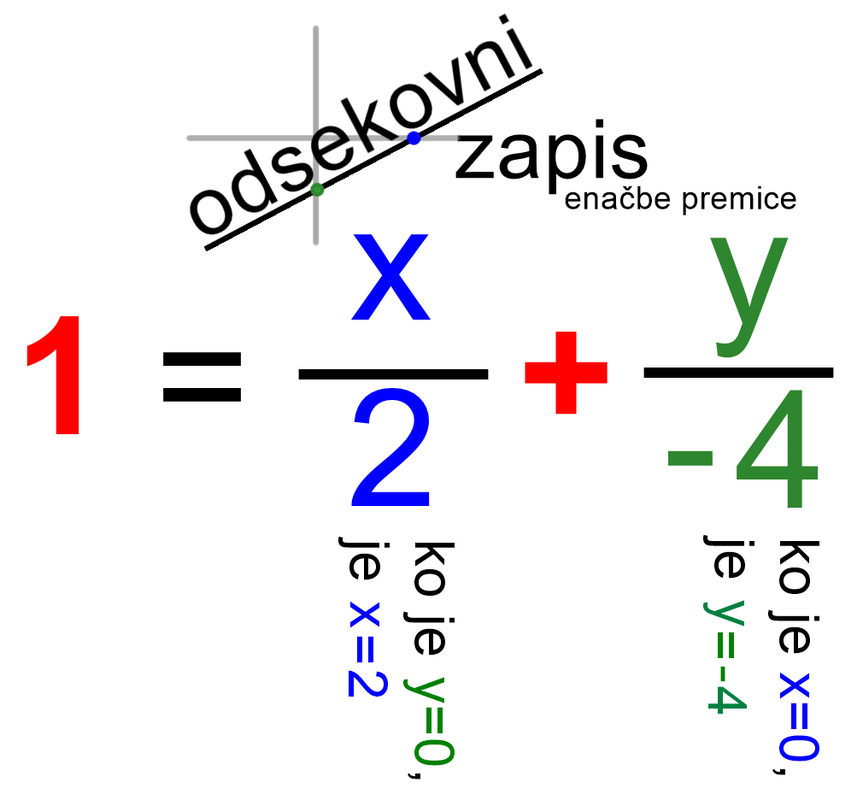
Ta zapis je po eni strani najbolj zakompliciran, po drugi strani pa si ga je najlažje predstavljati, saj je v neposredni povezavi z grafom funkcije. Tokrat je na svoji strani enačbe "osamljena" enica. Kaj nam ta enica pove?
|
ARHIV
May 2024
KATEGORIJE
All
|
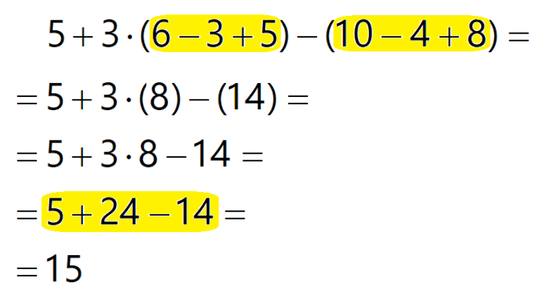
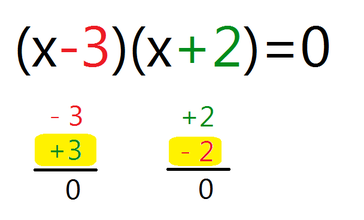



 RSS Feed
RSS Feed
