Enkrat je bilo v enem razredu ene šole eno dekle. In rada se je oblačila čisto "po svoje". Ker je bilo njenim sošolkam njeno oblačenje všeč, so jo pri tem posnemale.

In kje je tu matematika? 

​Dekle, ki se je oblačilo "po svoje", lahko označimo kot neodvisno, medtem ko so posnemovalke od nje odvisne.

Resno, kje je tu matematika?

Tako kot v zgornji zgodbi imamo tudi pri matematiki spremenljivke, ki so lahko odvisne ali pa neodvisne. Odvisne so seveda odvisne od - neodvisnih :) Odvisno spremenljivko običajno označimo z y, neodvisno pa z x. Na primer: y=2x+4.

No, sedaj pa imate matematiko :)

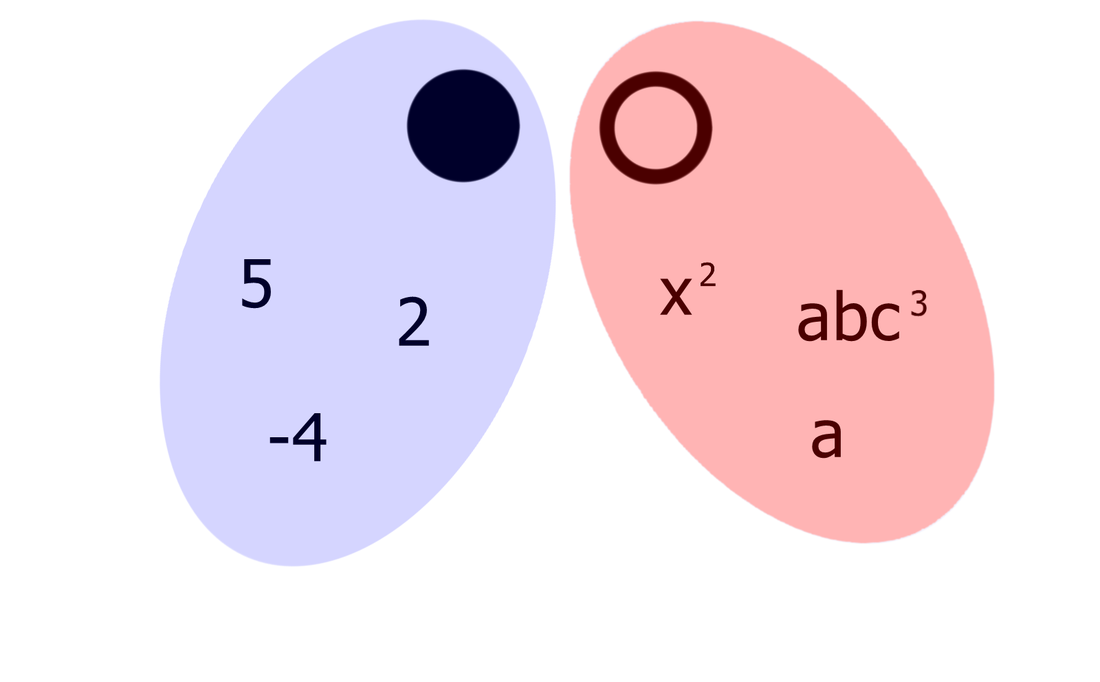
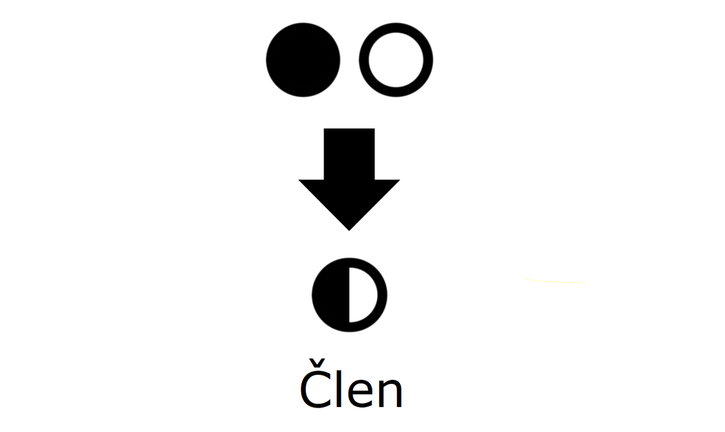
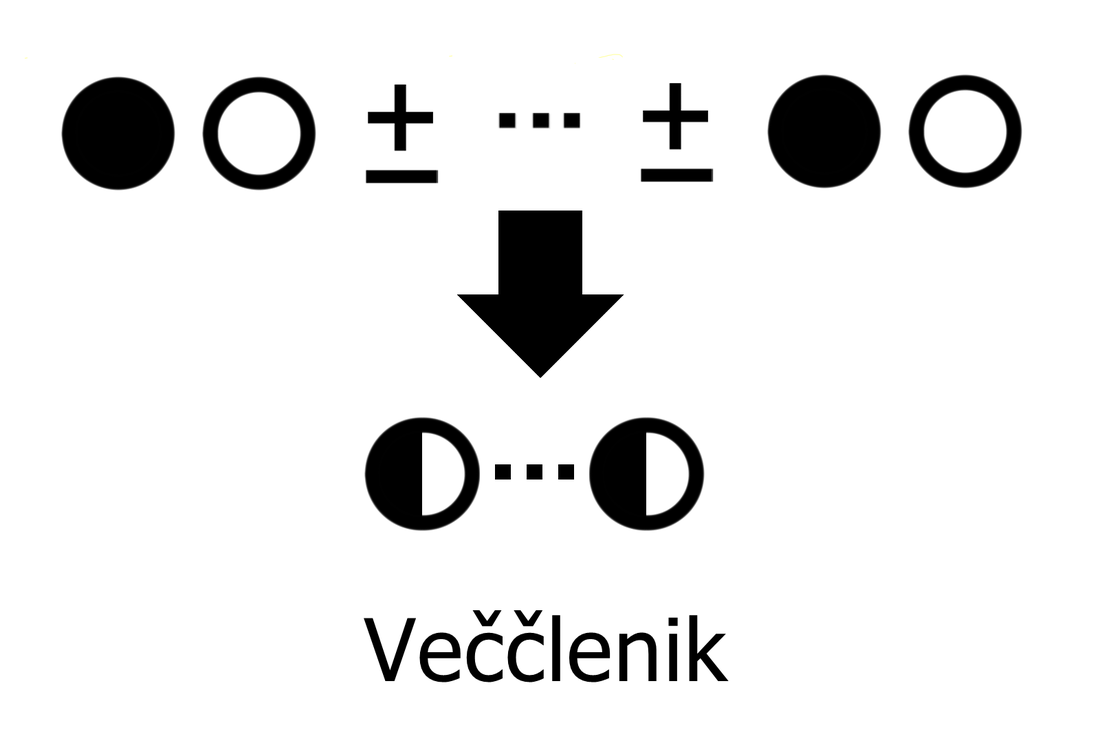
Izrazi, enačbe, neenačbe, poenostavljanje, razstavljanje... Nočna mora za tistega, ki ne razume, "šala-mala" za tistega, ki "se mu posveti". 

Skozi nepregledno množico pravil se bomo tokrat skušali prebiti s pomočjo simbolov, kar bo všeč predvsem tistim, ki ste bolj "vizualni tip".

Ponovitev

Najprej ponovimo pojem "člen".  Poenostavljeno rečeno je člen skupek številk in črk, med katerimi lahko nastopajo še simboli za množenje in deljenje ter eksponenti potenc in koreni. 

Ne pozabimo: znotraj člena simboli za seštevanje in odštevanje ter predznaka + in - ne nastopajo, razen če niso "ujeti" med oklepaje. So pa s simboli za seštevanje in odštevanje členi povezani med seboj!

Definicija simbolov

Začnimo z enočlenikom. Označimo ga z dvema krogoma:

• poln krog (predstavlja številko oziroma koeficient - številski faktor),
• prazen krog  (predstavlja črko oziroma spremenljivko).

Med njima je znak za množenje, ki pa ga ne pišemo. Pod njima je na sliki še nekaj primerov:

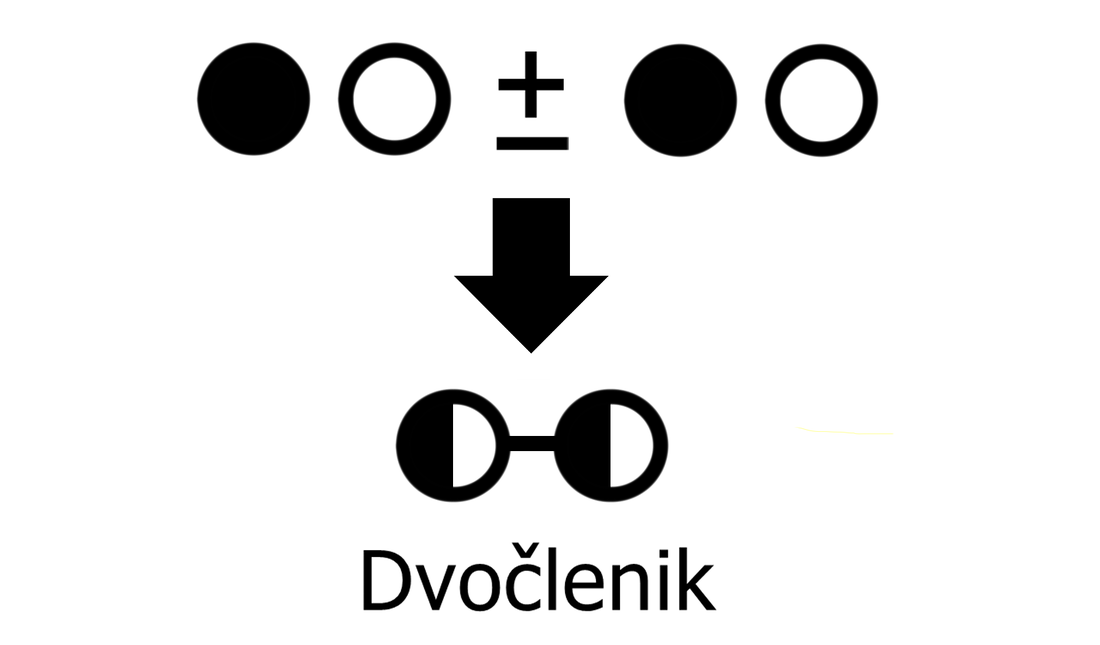
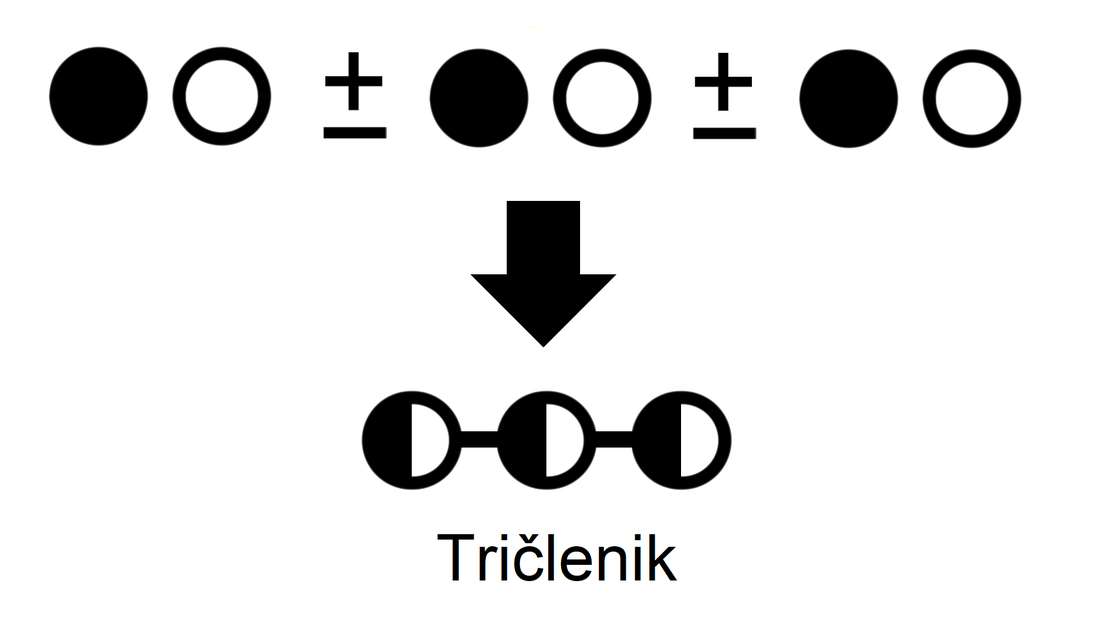
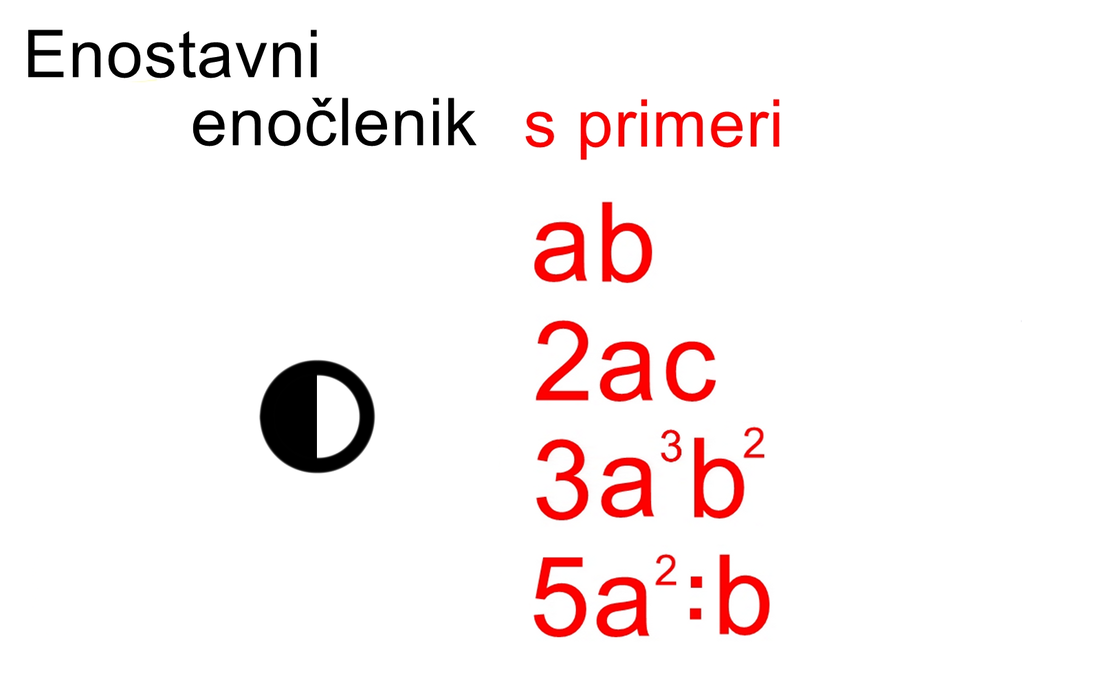
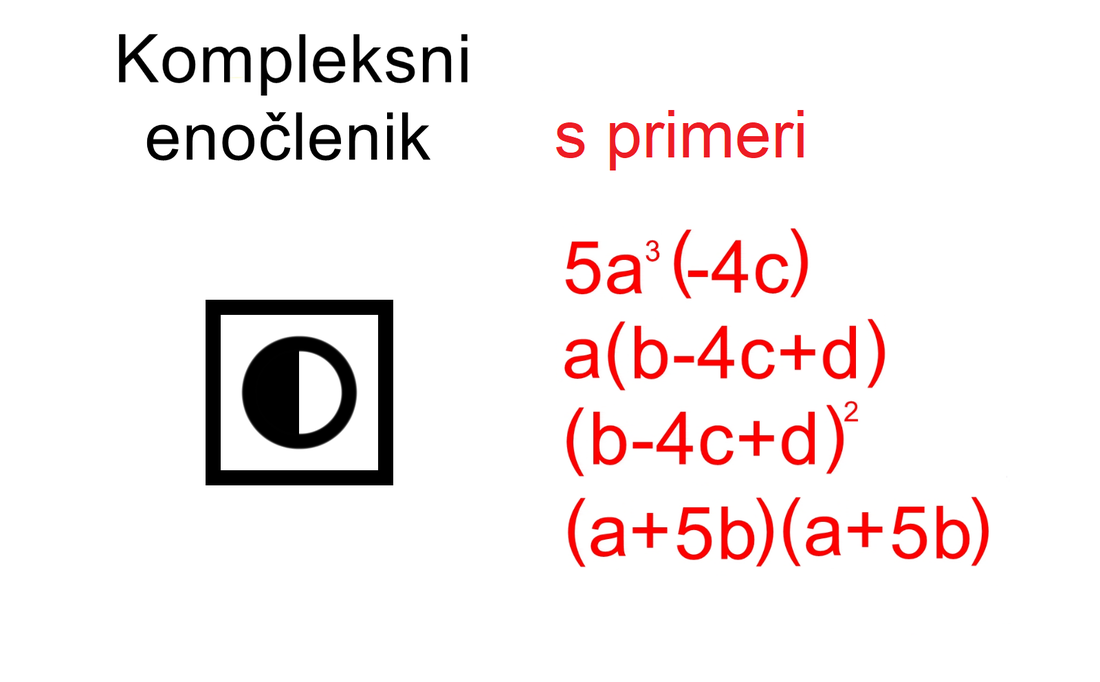
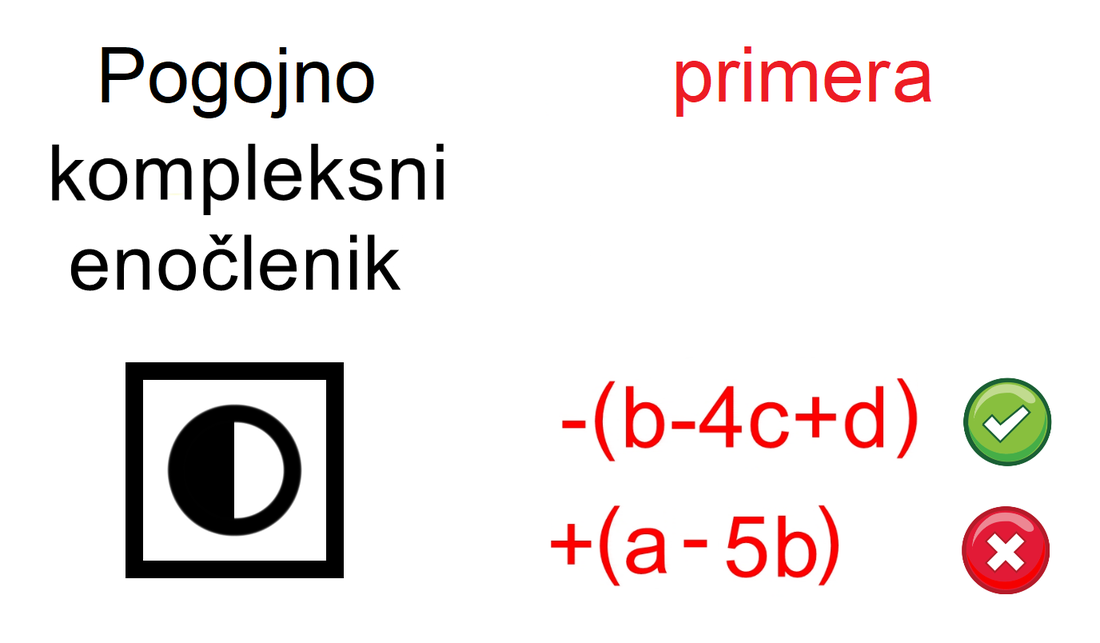
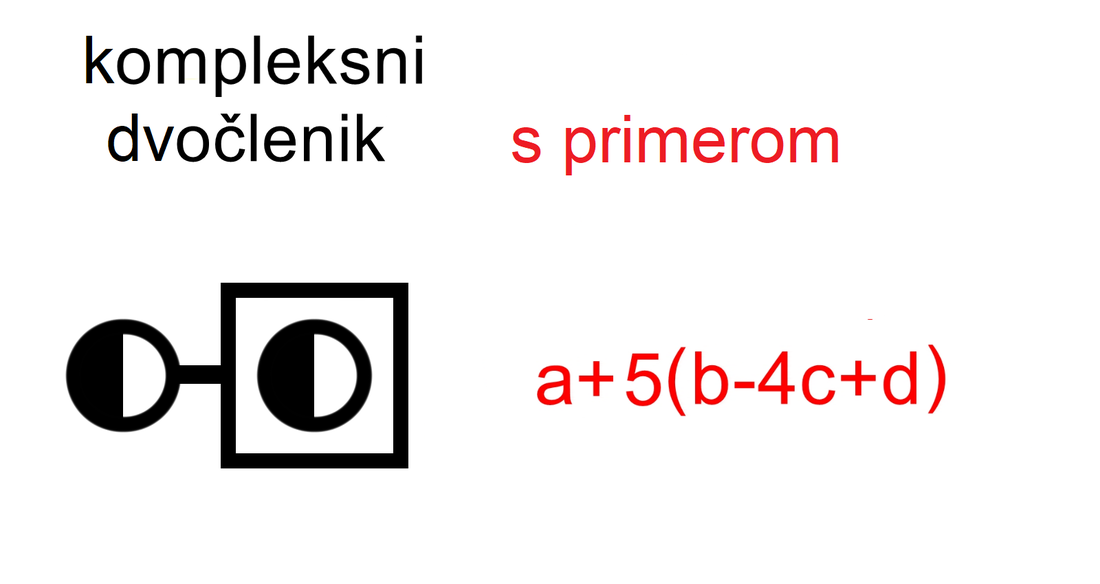
Če enočlenik ne vsebuje spremenljivke (take izraze srečamo v aritmetiki - samo številke, brez črk), rišemo le poln krog.

Za boljšo preglednost lahko kombinacijo polnega in praznega kroga poenostavimo:

Če med dva člena zapišemo + ali -, dobimo dvočlenik. Mi ga bomo označili takole:

V izrazih se pogosto pojavlja tudi tričlenik:

Ker je število členov lahko poljubno, dodajmo še simbol za veččlenik:

Enočlenika običajno ne predstavljata le koeficient in spremenljivka (številka in črka, na primer 5a), ampak je sestavljen iz več delov, pogosto z oklepaji (na primer a(b-c)(d+e)). Tak enočlenik bomo poimenovali "kompleksni enočlenik".

Seznam vseh simbolov je na naslednji sliki:

Oglejmo si nekaj primerov za enostavni in kompleksni enočlenik:

Če imamo le en oklepaj in pred njim stoji minus, je enočlenik pogojno kompleksni, saj gre v tem primeru za množenje oklepaja s številskim koeficientom -1 (posledično se po odpravi oklepaja vsem členom v oklepaju spremeni predznak):

- (b-4c+d) = (-1)·(b-4c+d) = -b+4c-d

Če pa pred oklepajem stoji plus, enočlenik ni kompleksen, saj oklepaj v tem primeru sploh ni potreben:

+ (a-5b) = a-5b

Če enostavni in kompleksni enočlenik združimo v dvočlenik, dobimo:

Zapis računskih pravil s simboli

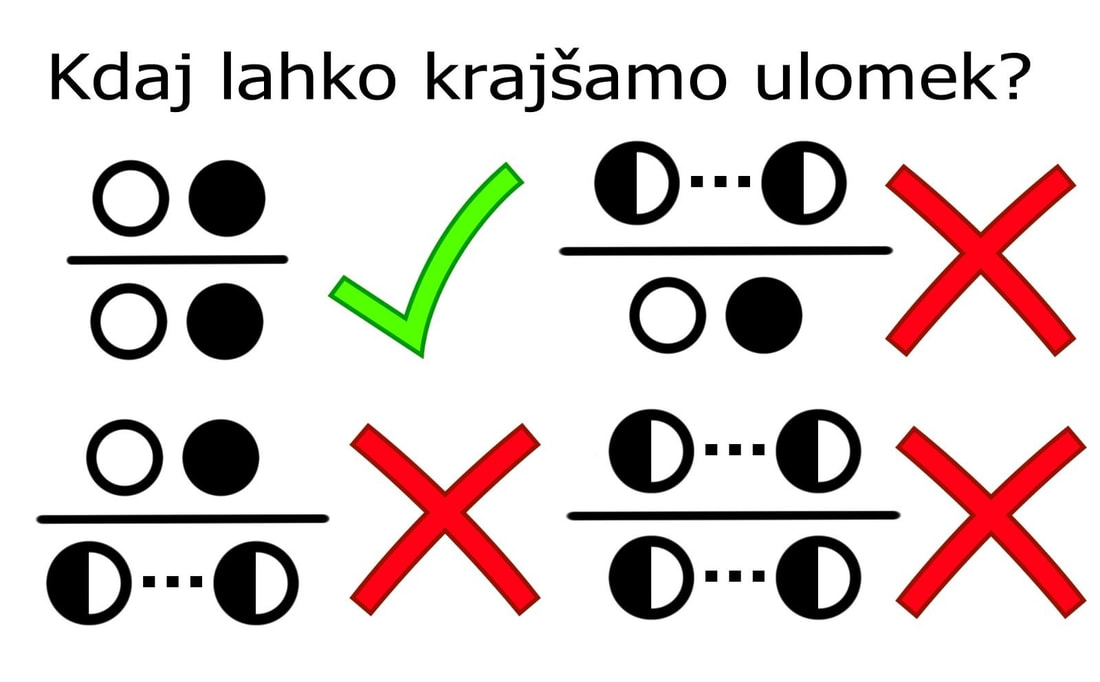
Za primer si oglejmo zapis pravila za krajšanje ulomkov.

Ulomek lahko krajšamo samo takrat, kadar je tako v števcu kot v imenovalcu enočlenik. Kadar imamo opravka z veččleniki, jih je potrebno najprej razstaviti:

Najprej v enačbi poenostavimo, kar se da, nato pa preverimo, kakšen je eksponent neznanke:

• če je najvišji eksponent neznanke enak ena (neznanka se npr. pojavlja le v obliki "x"), člene z neznanko postavimo na levo stran enačbe, člene brez neznanke pa na desno. Rešitev take (linearne) enačbe je le ena.
• če je najvišji eksponent neznanke enak dve ali več (neznanka se npr. pojavlja v obliki "x" in/ali "x²", in/ali "x³",...), vse člene postavimo na levo stran enačbe (in jih razstavimo), na desni pa naj bo samo 0. Rešitev bo toliko, kakršen je najvišji eksponent neznanke, v primeru deljenja enačbe z neznanko pa moramo seveda izločiti "prepovedane" rešitve
  

Vsak matematični izraz lahko preoblikujemo v dve skrajnosti:

• če na koncu dobimo produkt faktorjev, je to razstavljanje, razcepljanje oz. faktorizacija; na primer (x-2)(x+3)
• če na koncu dobimo vsoto/razliko členov, je to poenostavljanje, razširjenje oz. razčlenjenje; na primer x^2+x-6

V praksi dobimo na testu izraz, ki je "nekje vmes", potem pa ga moramo bodisi poenostaviti, bodisi razstaviti.

Ponovimo:
Faktorji so med seboj ločeni z znakom za množenje ali deljenje.

• Lahko so sestavljeni iz ene same številke (koeficienta) ali/in ene ali več črk (spremenljivk) na poljubno potenco (npr. 2x^2),
• lahko pa so sestavljeni iz produktov črk in številk, ločenih s plusi oziroma minusi - v tem primeru morajo biti faktorji ločeni z oklepaji (npr. (2x+2)(x^2-3))

Členi so med seboj ločeni z znakom za seštevanje ali odštevanje.

• sestavljeni so iz faktorjev, ti pa so spet lahko dveh vrst (glej zgornji dve alineji)

"Tehnika", ki jo uporabimo pri seštevanju dveh algebrskih ulomkov, pri katerih imenovalca nimata skupnega faktorja

[slika sledi...]

Ponovimo:
Algebrski izraz je smiseln zapis, sestavljen iz spremenljivk (največkrat je to "x"), števil, računskih operacij (+, -, krat, deljeno) in oklepajev, na primer: (x^2-2x+5)*x
Aritmetični izraz je poenostavljeno rečeno algebrski izraz brez spremenljivk (črk). 
Algebrski ulomek ima v števcu in/ali imenovalcu algebrski izraz.

• Absolutna vrednost podanega števila je vedno pozitivna.
• Če pa imamo podano absolutno vrednost števila in iščemo "originalno" število, sta rešitvi vedno dve - ena pozitivna in ena negativna, saj je absolutna vrednost tako pozitivnega kot negativnega števila - pozitivna.

Drugo alinejo si lahko predstavljamo tudi na naslednji način: Ko pridemo domov, je skleda z jabolki vedno prazna. Za to pa vedno obstajata dva scenarija - lahko da je bila prazna že zjutraj, lahko pa je bila skleda zjutraj polna in je jabolka potem nekdo pojedel 

Običajno iščemo najmanjši skupni večkratnik malih števil, rezultat pa je običajno neko veliko število (kljub temu, da govorimo o najmanjšem skupnem večkratniku). No, vsaj oznaka v (mala črka) je "v sorodu" z nečim malim.

Iskanje najmanjšega skupnega večkratnika si lahko poenostavimo na naslednji način:

• razcepimo podana števila na prafaktorje (začnemo z 2, nadaljujemo s 3, 5 in 7,...dlje nam običajno ni potrebno iti
• enake prafaktorje posameznega števila zapišemo s potenco
• obkrožimo vse prafaktorje z najvišjim eksponentom (ne glede na to, kateremu številu pripadajo)
• zmnožimo obkrožena števila in dobimo najmanjši skupni večkratnik podanih števil

Običajno iščemo največji skupni delitelj velikih števil, rezultat pa je običajno neko malo število (kljub temu, da govorimo o NAJVEČJEM skupnem delitelju). No, vsaj oznaka D (velika črka) je "v sorodu" z nečim velikim.

Poleg običajnega iskanja največjega skupnega delitelja si lahko pomagamo tudi s preprostim krajšanjem števil. Števila delimo s praštevili; začnemo z 2, nadaljujemo s 3 in 5...no, dlje nam običajno niti ni več potrebno iti. Števila krajšamo toliko časa, da nimajo nobenega skupnega delitelja več (pravimo, da so si tuja).
Če zmnožimo vsa praštevila, s katerimi smo krajšali prvotna števila, dobimo največji skupni delitelj.