|
»Hm«, boste rekli, »a nismo v šoli rekli, da velja zgolj za seštevanje in množenje? Ja. In ne. :) Če odštevanje obravnavamo strogo kot odštevanje in deljenje kot deljenje, potem ne moremo splošno reči, da zanju velja zakon o zamenjavi. Če pa:
A pozor! Računsko operacijo pred številom, ki ga želimo »nesti drugam«, moramo v tem primeru »vzeti s seboj«! Oglejmo si dva primera. V prvem želimo odštevanje postaviti na konec računa, da ga bomo izvedli nazadnje. To lahko storimo, a ne pozabimo minusa pred številom 5! V drugem primeru pa želimo deljenje izvesti prej, da ne bo deljenec prevelik. Število 4 lahko postavimo takoj za 12, a ne pozabimo »s seboj nesti« tudi znaka za računsko operacijo deljenja! Da me ne boste "prijeli za besedo": V matematičnem členu po Wikipediji v členu lahko nastopata zgolj številski operaciji množenja in potenciranja. Kaj pa deljenje? Če si deljenje z nekim številom (v našem primeru s 4) predstavljamo kot množenje z ulomkom, ki ima to število v imenovalcu, števec pa enak 1 (v našem primeru 1/4), pa imamo čisto pravi člen s štirimi faktorji: 12, 2, 3 in 1/4.
0 Comments
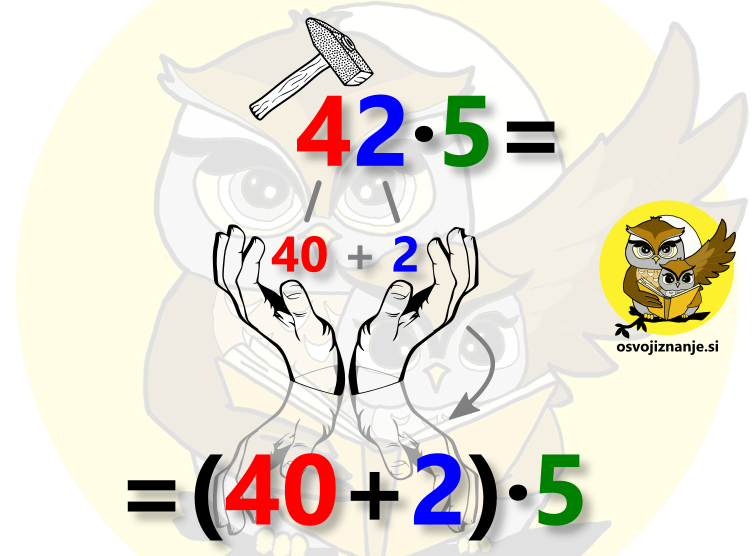
O tem, kaj je distributivnost, lahko nekaj več preberete tule, mi pa si poglejmo kar primer. Izračunajmo račun 42 krat 5. Poštevanka nam tu direktno ne more pomagati, saj jo znamo le do 10 krat 10, si pa lahko pomagamo tako, da razdelimo prvi faktor na dva dela (42 razdelimo na štiri desetice in dve enici), katera potem ločeno množimo z drugim faktorjem (v našem primeru 5) in na koncu seštejemo (po distributivnostnem zakonu). Da bo vse skupaj še lažje, si izmislimo zgodbico. 🙂 Recimo, da s kladivom udarimo po večjem od števil (42), nakar to razpade v števili 40 in 2, ki ju ujamemo v roko in postavimo v oklepaj: Števil ni nujno drobiti na vrednosti pod 10, saj poštevanka zajema celoštevilske faktorje do vrednosti 10. Močno si lahko pomagamo že z razčlenitvijo na večkratnike desetiških enot. Mi smo število 42 s tem namenom razdelili na 40 (4 krat 10) in 2. Namesto množenja števil 42 in 5 bomo tako s 5 zmnožili števili 40 in 2 ločeno, rezultata množenja pa na koncu sešteli. Nadaljujmo našo zgodbico od včeraj. 😉 Petico si na primer predstavljajmo kot psa, na katerega z vsake številke v oklepaju skoči ena bolha. Vsak skok pomeni eno množenje. Prvo je 40 krat 5, drugo pa 2 krat 5: Sedaj moramo izračunati le še preprost računski izraz (ne pozabimo, da ima množenje prednost pred seštevanjem) in smo končali. 🙂 Za tak način množenja torej potrebujemo le znanje poštevanke, seštevanja in množenja z večkratniki potenc števila 10. Zakaj iz 4 ∙ 5 = 20 sledi, da je 40 ∙ 5 = 200? Preprosto. 40 ∙ 5 lahko zapišemo tudi kot 4 ∙ 10 ∙ 5 oziroma 4 ∙ 5 ∙ 10 (zakon o zamenjavi) oziroma 20 ∙ 10 (zakon o združevanju), pri množenju z 10 pa vemo, da v rezultatu "pridelamo" dodatno ničlo na desni strani (oziroma premik decimalne vejice v desno, kadar računamo z decimalnimi števili).
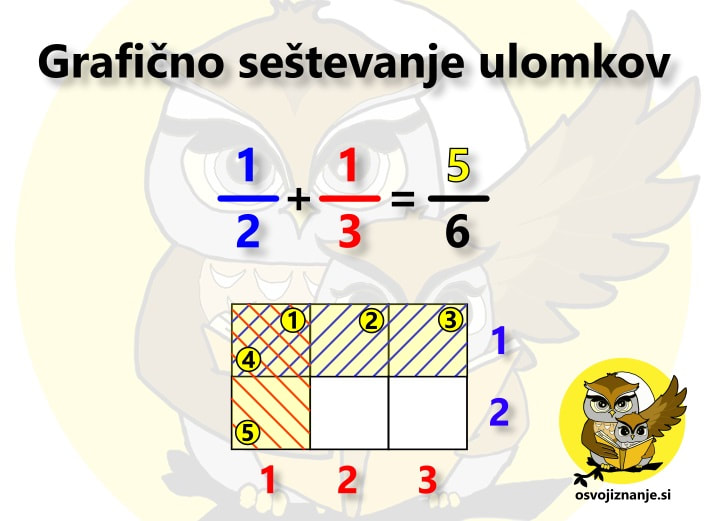
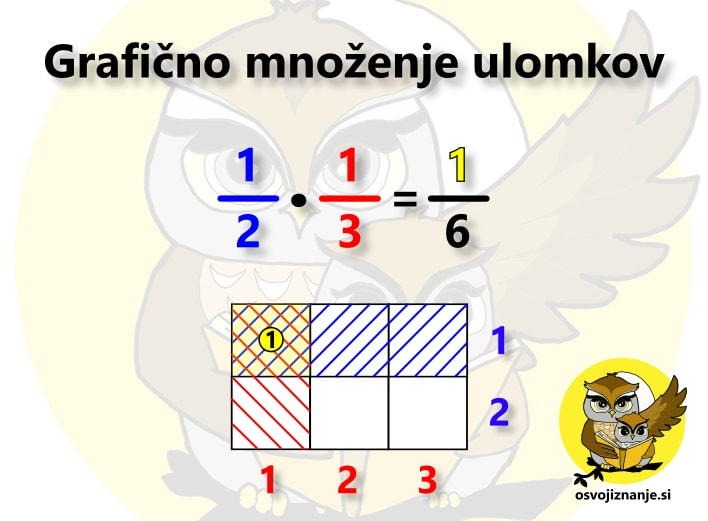
Na koncu še vprašanje za vas. V našem primeru smo delna zmnožka na koncu sešteli. Pri katerih številih, recimo dvomestnih, pa bi bil račun lažji, če bi uporabili odštevanje? (Kadar je enica večja od 5, npr. pri računu 48 ∙ 5.) ... oziroma uporaba logike pri uri aritmetike. Pri seštevanju ulomkov »na klasičen način« vemo, da jih moramo najprej »spraviti na skupni imenovalec«, nato pa sešteti števce le-teh. Na koncu ulomek, ki predstavlja vsoto, še okrajšamo. Kako pa bi to storili grafično? Oglejmo si račun 1/2+1/3. Ker ulomek predstavlja del celote, eno polovico lahko predstavimo tako, da celoto razdelimo na dva enaka dela in enega pobarvamo. Z eno tretjino storimo podobno, le da celoto razdelimo na tri enake dele. Kako pa bi naenkrat lahko predstavili oba ulomka? Z dvodimenzionalnim poljem oziroma tabelo. S stolpci prikažemo en ulomek, z vrsticami pa drugega. V našem primeru torej potrebujemo tabelo z dvema stolpcema in tremi vrsticami (lahko storimo tudi obratno, saj za vsoto velja zakon o zamenjavi). Modra šrafura na sliki predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3. Sedaj pa »vklopimo logiko«. V Booleovi algebri simbol »+« pomeni disjunkcijo oziroma logični »ali«. V izjavni logiki (angl. propositional logic) to povezavo označimo z znakom »∨«, v teoriji množic pa z znakom »∪«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »∥« ali zgolj angleškem izrazu »OR«. Kaj to pomeni za našo tabelo s prikazom ulomkov? S pomočjo uporabe logike lahko iz nje neposredno zapišemo rezultat našega računa. Ker ima tabela 6 polj, je imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Kaj pa števec? Ker imamo logično relacijo »ali«, moramo prešteti vsa polja, ki so šrafirana ali modro ali rdeče. Eno polje je šrafirano z dvema barvama, torej ga moramo šteti dvakrat. Imamo torej eno modro, dve rdeči in eno dvobarvno šrafirano polje, skupaj torej 1+2+2 oziroma 5 polj. Števec je torej 5, kar pomeni, da je vsota enaka 5/6. Pri množenju ulomkov »na klasičen način« pa zmnožimo tako števce kot imenovalce ter okrajšamo, »kar se da«. Za primer uporabimo ista ulomka, le da ju tokrat zmnožimo. Iščemo torej produkt 1/2 · 1/3. Ulomka predstavimo na povsem enak način kot pri seštevanju, le rezultat bomo prebrali drugače. Zopet imamo torej tabelo z 2 stolpcema in 3 vrsticami, kjer modra šrafura predstavlja števec ulomka 1/2, rdeča pa števec ulomka 1/3. Ponovno »vklopimo logiko«. V Booleovi algebri simbol »*« pomeni konjunkcijo oziroma logični »in (hkrati)«. V izjavni logiki to povezavo označimo z znakom »∧«, v teoriji množic pa z znakom »∩«. Poznavalci digitalnega sveta omenjeno relacijo prepoznajo tudi v znaku »&« ali zgolj angleškem izrazu »AND«. S pomočjo naše tabele zapišimo še rezulat. Ker ima tabela 6 polj, je tudi tu imenovalec vsote enak 6, saj gre za celoto, razdeljeno na 6 (enakih) delov. Pri števcu pa bo nekoliko drugače. Ker imamo logično relacijo »in hkrati«, moramo prešteti vsa polja, ki so šrafirana tako modro kot rdeče. Tako je le eno polje, kar pomeni, da je števec enak 1. Zmnožek ulomkov 1/2 in 1/3 je torej enak 1/6. Omenjena metoda je mogoče nekoliko daljša od »klasične«, saj je tu in tam potrebno kakšen rezultat še dodatno okrajšati, nam pa omogoča zelo dober vpogled v koncept računanja z ulomki, česar nam »piflarski« postopki ne nudijo.
Ste pogrešili odštevanje in deljenje? Odštevanje je »pokrito« s prištevanjem nasprotne vrednosti, deljenje pa z množenjem z obratno vrednostjo. Na koncu pa še vprašanje za vas. Kako bi grafično predstavili vsoto oziroma zmnožek treh ulomkov? Vedno bolj se zavedamo, da je vizualizacija zelo pomembna za razumevanje matematičnih zakonitosti. Pa tudi kakšnih drugih. Ampak, ostanimo zaenkrat pri matematiki. Konkretneje, pri osnovnih računskih operacijah. Načinov za vizualno predstavitev seštevanja, odštevanja, množenja in deljenja je kar veliko, zato smo včasih v dilemi, katerega uporabiti. Seveda je najbolje, da si vsakdo izbere takega, ki ustreza prav njemu, a vseeno je nekje potrebno začeti. ;) Sam ponavadi začnem z dvema modeloma oziroma didaktičnima pripomočkoma (če ju imamo na voljo v fizični obliki), to sta:
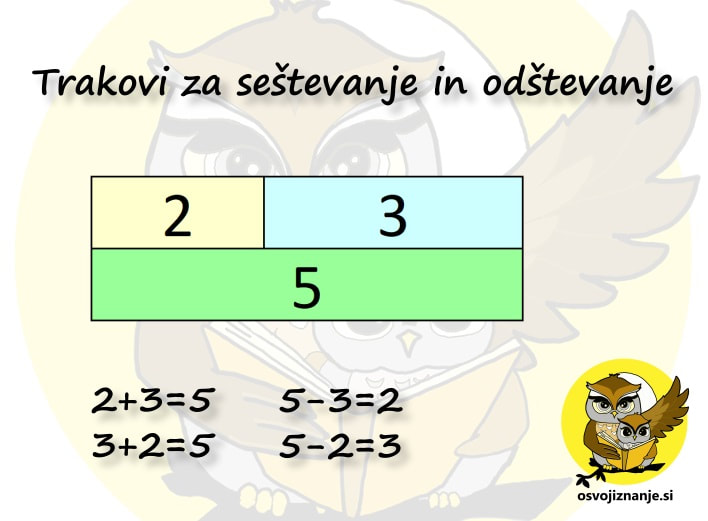
Glavna razlika med trakom in ploščicami je dimenzija. Trak se razteza le v eni smeri, medtem ko je polje ploščic dvodimenzionalno. Če trakove zlagamo enega za drugim, nam celotna dolžina take »kače« predstavlja vsoto posameznih trakov, s čimer ponazorimo seštevanje. Če trakove zlagamo vzporedno, pa jih med seboj lahko primerjamo. Se sprašujete, kje smo izgubili odštevanje? ;) Odštevanje najlažje ponazorimo z razliko med dolžinama dveh trakov. Kljub temu, da ne govorim o merjenju, ampak o računanju, sem že dvakrat omenil dolžino. Malo iz navade, malo pa nalašč. ;) Seštevanje in odštevanje si namreč v naravi najlažje predstavljamo prav z merjenjem razdalje. Če na primer najprej prehodim 3 kilometre, nato pa še 2, sem skupaj prehodil 3+2, torej 5 kilometrov (seštevanje, vsota). Če je sosednja vas oddaljena 6 kilometrov, pa moram do nje prehoditi še 6-5, torej 1 kilometer (odštevanje, razlika). Kaj pa množenje in deljenje? Za množenje vemo, da predstavlja seštevanje več enakih števil hkrati, lahko bi mu rekli tudi »turbo seštevanje«. :) Zakaj bi recimo preštevali 56 rozin, ko pa jih lahko zložimo v 7 vrstic po 8 ali 8 vrstic po 7 rozin? Ja, 7 krat 8 je isto kot 8 krat 7, le gledamo nekoliko z druge perspektive. In ja, govorimo o poštevanki. :) Poštevanka ni nič drugega kot vsi možni računi množenja s faktorji od 1 do 10. In če želimo pri računanju imeti »doživljenjski turbo pogon«, se jo je dobro dobro naučiti. Ja, dobro je zapisano dvakrat, ne gre za slovnično napako. :)
Pri deljenju pa imamo prav tako opravka z več enakimi števili, le da jih tu ne seštevamo, ampak neko večje število razdelimo na več enakih manjših števil. Včasih to (v množici celih števil) ni mogoče, zato govorimo o deljenju z ostankom. Pri deljenju z ostankom eno od števil vedno »nasrka«, saj je manjše od ostalih. Saj poznate tisto, trije starejši bratje in četrti »mulc«, ki je komaj iz plenic ... nikoli nima prav. ;) Glede na povedano množenje torej najlažje predstavimo z zlaganjem v stolpce in vrstice. Kaj pa bi zlagali? Ploščice. Ali, če želite, polagali, tako kot tiste v kopalnici. ;) Z deljenjem pa te ploščice razdelimo, podolgem ali počez. O tem, da za seštevanje obstajata dva (glavna) postopka in da eden ne more nadomestiti drugega, sem že pisal, zato le na kratko povzamem: Seštevanje v vrsti je močno povezano z razumevanjem koncepta (desetiške enote, mestnovrednostni koncept), medtem ko je seštevanje v stolpcu zgolj na pamet naučen matematični postopek. Za prvega bi lahko rekli, da je »človeku bolj prijazno« in ga lahko izvajamo tudi ustno, medtem ko je drugi primeren zgolj za pisno računanje. Slednji tudi ni preveč perspektiven, saj računanje v taki obliki vse bolj prevzemajo računalniki. Zato povejmo raje nekaj več o seštevanju v vrsti in sicer tistem »na pamet«. Ustno seštevanje je vsekakor koristno usvojiti, saj je hitrejše, pa še zvezka in pisala nimamo vedno pri roki. Na primer v trgovini, ko lovimo znesek 20 evrov, da bi si pridobili bonus, a ne želimo iti niti centa čez. ;) Zna pa biti za marsikoga zahtevnejše od pisnega računanja, se ga velja lotiti postopoma. Na začetku v vrsti lahko seštevamo pisno. Najprej seštejemo posamezne desetiške enote, nato pa še vse skupaj: Ko zadevo obvladamo že nekoliko bolje, si pa lahko zapišemo le še vmesne zneske (recimo najprej le vsoto stotic, ki ji nato dodamo vsoto desetic in nazadnje prištejemo še enice), ostalo pa poskusimo izračunati ustno. Z ustnim seštevanjem se naučimo tudi t.i. »inženirskega računanja«, kjer je velikokrat potrebno narediti hitre ocene rezultata. V dolgi vrsti v trgovini za to sicer ni potrebe, a vseeno. :)
Za konec pa bi poudaril še eno prednost seštevanja v vrsti, to je večja svoboda pri računanju. Za marsikoga to sicer niti ni ne vem kakšna prednost, saj od nas zahteva »skok iz cone udobja«. Na drugi strani se moramo pri seštevanju v stolpcu strogo držati postopka, kar po svoje pomeni določeno stopnjo varnosti, težava pa nastane, če postopek pozabimo. Če poznamo koncept, si pri seštevanju pomagamo lahko tudi kako drugače, recimo z izposojanjem številskih enot, dopolnjevanjem do desetice ipd. Seštevanje v vrstici bi lahko poimenovali kar »kreativno seštevanje«. V učbenikih so take naloge ponavadi označene s »Spretno izračunaj ...« Pri teh vam bo kalkulator prej v napoto kot v korist. ;) V tokratnem prispevku najprej vprašanje za vas. Na spodnji sliki je isti račun rešen na dva načina. Za katerega menite, da je boljši oziroma lažji, bolj razumljiv in si ga je lažje zapomniti ter za dlje časa? S čim vas en ali drug postopek "prepričata"? V nadaljevanju si bomo oba podrobneje ogledali. Seštevanje "v vrsti" Seštevanje "v vrsti" (včasih slišimo tudi izraz "vodoravno seštevanje") se bo mogoče komu zdelo zastarelo. Starši se verjetno v večini spomnimo predvsem drugega načina ("v stolpcu"), a prvi v sebi skriva več, kot si morda predstavljamo. Tovrsten postopek je namreč osnova za dejansko razumevanje tega, kar se pri tem računskem postopku dogaja s števili - razumevanje koncepta seštevanja. Pri seštevanju v vrsti najprej seštejemo velike desetiške enote, nato pa po vrsti vedno manjše. V našem primeru seštevamo tri dvomestna števila, tako da najprej seštejemo vse tri desetice (označene rdeče), zatem pa še vse tri enice (označene modro). Na ta način možgane razbremenimo razmišljanja pri prehodu čez desetico. 60 + 19 je recimo opazno lažji račun, kot pa 25 + 36 + 18. Če tudi krajši zapis za nas pretrd oreh, ga lahko še nadalje poenostavimo. V našem primeru: 60 + 19 = 60 + 10 + 9. Druga poenostavitev pride v poštev recimo pri kakšnem prehodu čez stotico, tisočico ... Recimo v primeru 90 + 14. Veliko lažje je k 100 prišteti 4 kot pa k 90 prišteti 14. Miselni tok seštevanja je pri tem postopku zelo podoben računanju "na pamet", kar verjetno večina od nas počne na primer v trgovini, ko sproti računamo, koliko je vredno blago, ki ga zlagamo v nakupovalni voziček. Seštevanje "v stolpcu"
Seštevanje "v stolpcu" marsikomu izgleda enostavneje od seštevanja "v vrsti", a nima kaj dosti skupnega z razumevanjem koncepta seštevanja. Glavna težava omenjene metode je seštevanje "z napačnega konca", vsaj kar se številskih predstav tiče. Pri seštevanju v stolpcu namreč računamo od desne proti levi oziroma od manjših desetiških enot proti večjim, kar po domače povedano "ni možganom prijazno". Miselni tok gre pri računanju "na pamet", ki zahteva (in tudi vzpodbuja) dobre številske predstave, večinoma v obratni smeri. Spomnimo se štetja denarja. Pri tem je lažje najprej sešteti večje vrednosti in nato prišteti še drobiž, kot pa obratno. Pri računanju "v stolpcu" poseben postopek s "prenašanjem naprej" omogoča, da števila zlahka seštejemo, tudi če številskih predstav (še) nimamo dobro razvitih. To na prvi pogled izgleda obetavno, a je na dolgi rok zelo problematično. Otrok, ki nima dobro razvitih številskih predstav, bo sicer nekaj časa lahko še uspeval v matematiki, a bo učenja "na pamet" vedno več, napake pa vedno bolj izrazite. Na neki točki lahko preprosto zaide v slepo ulico, iz katere pa je pot zelo naporna. "Znak za alarm" pri razumevanju je recimo lahko že nepravilno podpisovanje (pravilno je enice pod enice, desetice pod desetice ...) ali napačno "prenašanje" pri prehodu čez desetico (recimo prenos enice namesto desetice). Težava nastane tudi, če postopek pozabimo. Brez dobrih številskih predstav ga bomo zelo težko ponovno priklicali iz spomina. V času pred razcvetom žepnih računalnikov je bil ta postopek praktično edini način za hitro seštevanje večmestnih števil, danes pa so ga v večini nadomestili računalniški algoritmi, zato bo v prihodnosti vedno manj pomemben. V našem primeru najprej seštejemo (modre) enice. Rezultat je 19, kar pomeni, da 9 zapišemo, desetico (1, zapisana z manjšo pisavo) pa "nesemo naprej" v stolpec levo ter jo prištejemo k seštevku desetic (2 + 3 + 1 = 6), skupaj torej 7. In dobimo rezultat 79. Če postopka ne razumemo, nam ta predstavlja zgolj skupek navodil brez pomena. Če se med računanjem zmotimo, večinoma tega niti ne opazimo, ko pa se »zatakne«, nam pa ne preostane drugega, kot da vse skupaj pustimo in gremo reševat naslednjo nalogo. Ob razumevanju koncepta, ki se »skriva« za postopkom, pa lahko hitro opazimo, če gre kaj narobe, najpomembnejše pa je to, da se v primeru težav lahko sami »rešimo«. Oglejmo si postopek pisnega množenja z dvomestnim številom. Za primer vzemimo račun 123 · 45. Pri pisnem množenju 123 najprej množimo s 4, nato pa še s 5: Zakaj je spodnja vrstica (množenje s 5) zamaknjena v desno? V bistvu ni, ker je zgornja zamaknjena v levo. :) Zakaj? Zato, ker množenje s 4 v bistvu ni množenje s 4, ampak s 40 (več o tem nekoliko kasneje). S tem namenom sem na skrajno desno stran zgornje »zelene« vrstice tudi zapisal ničlo, a narahlo, saj jo (vsaj v naših šolah) ne pišemo. Prištevanje 0 v zadnjem koraku postopka, do katerega še pridemo, namreč ne spremeni končnega rezultata. Če je 123 · 4 enako 492, je 123 · 40 enako 4920, saj z 10 preprosto množimo tako, da na desni strani prvega faktorja pripišemo ničlo, 123 · 5 pa je 615. Na koncu »zeleni« vrstici še seštejemo in celotni račun se glasi: Zakaj moramo »zelena« zmnožka sešteti? Distributivnostni zakon pravi, da je zmnožek vsote dveh števil s tretjim številom enak vsoti posameznih zmnožkov prvih dveh števil s tretjim številom. Zapleteno? Prav imate. Zato sem o tem pripravil posebno razlago, kjer vam bo postalo vse jasno. :) Če število 45 razdelimo na desetice in enice, dobimo vsoto dveh števil iz našega zakona (ja, tistega, z neznansko zapletenim imenom :) ), števili med črtama pa sta posamezna zmnožka, za katera vemo, da ju moramo na koncu sešteti. In točno to v postopku tudi naredimo. Zapis z upoštevanjem distributivnostnega zakona se tako glasi: Dodatna vprašanja:
Naslov izgleda zapleteno, pri razlagi pa se bom potrudil, da ne bo tako :) Za pisno deljenje z dvomestnim številom obstaja več metod (za eno izmed njih sem posnel tudi video), tokrat pa si oglejmo metodo s približki. Metoda je primerna predvsem za delitelje z majhno oziroma veliko vrednostjo enice, saj je tu relativna napaka majhna in nam ne bo potrebno toliko radirati. Zakaj, si lahko ogledate tule, kjer sem to metodo uporabil pri delitelju 14 in sem imel kar veliko dela :) Mi pa izračunajmo naslednji račun: 279 : 31 Najprej ugotovimo, s kolikšnim delom deljenca pričeti računanje. Ker 31 ne gre v 27 niti enkrat, moramo vzeti vse 3 števke deljenca, zato »kljukice« (z njo ločimo del deljenca, na katerem izvajamo operacije, od preostalega dela) ne bomo potrebovali, s podpisovanjem pa bomo začeli pod enico deljenca. Za matematične navdušence (ostali lahko nadaljujete v naslednjem odstavku): Načeloma bi lahko začeli tudi le z dvema števkama najvišje mestne vrednosti (2 in 7), a bi bila prva števka količnika 0 (števka z najvišjo mestno vrednostjo), za 0 pred številom pa vemo, da je vseeno, če ga ni (za ničlo na najnižji mestni vrednosti pa seveda vemo, da mora biti tam). Računanje bomo torej pričeli z »delnim« računom 279:31 (v našem primeru je to kar celoten račun). Sedaj vas pa verjetno že zanima, kje se skriva približek iz naslova in zakaj ga sploh uporabimo. 279:31 je razmeroma težak račun, če pa 279 zaokrožimo na 280, 31 pa na 30, dobimo: 280 : 30 Če tako deljenec kot delitelj delimo z 10, se račun ne spremeni, zato dobimo nov, lažji račun: Spomnimo se na krajšanje ulomkov, za katere vemo, da so v bistvu računi deljenja: Tu lahko uporabimo znanje poštevanke, saj vemo, da je 9·3 enako 27, 10·3 pa 30. 28 je malo nad 27, torej lahko rečemo, da je 28:3 enako 9 »in še malo zraven«. Na tem mestu ne smemo pozabiti, da naš račun ni 28:3, ampak 279:31, zato računamo naprej na »originalnem« računu. Približek smo uporabili samo zato, da smo lažje ugotovili, približno (!) kolikokrat gre 31 v 279. Ker je 28 nekaj več kot 9·3 (oziroma 280 nekaj več kot 9·30), za 31 lahko rečemo, da gre približno 9-krat v 279 in zapišemo prvo števko količnika: 279 : 31=9? Ker smo prvo števko količnika ("uporabili" smo že celotni deljenec, zato je ta edina) zgolj ocenili, še nismo prepričani, da je prava, jo je potrebno preveriti z obratno računsko operacijo - množenjem (če število delimo in nato množimo z istim številom, dobimo nazaj prvotno število). Pozor: tega preverjanja z množenjem ne smemo mešati z množenjem v preizkusu, ki sledi na koncu računa, saj tu preverjamo vsako števko količnika posebej, v preizkusu pa celoten račun. Pa preverimo: 1·9 je 9 in nič ne manjka več do 9, zato pod enico deljenca zapišemo 0. 3·9 je 27 in nič ne manjka več do 27, zato tudi pod desetico deljenca zapišemo 0. Ostanka ni, saj je 31·9 enako 279, kar kasneje seveda lahko preverimo tudi s preizkusom. 279 deljeno z 31 je torej res 9. Ker sta bila naša približka (280 in 30) relativno blizu "originalnima" vrednostma (279 in 31), nam je "uspelo" že v prvem poskusu, sicer pa bi morali še malo radirati :)
Za konec še nekaj vprašanj za razmislek:
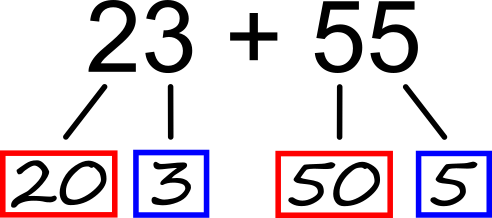
Kaj so to številska drevesa? Po domače povedano so to drevesa, na katerih namesto jabolk rastejo števila, obrnjena pa so z glavo navzdol. Vam je zdaj kaj bolj jasno? Manj? :) Pravijo, da slika pove več kot 1000 besed, zato si poglejmo primer. Razdelimo število 123 na desetiške enote in ga zapišimo v obliki: Predstavitev števila na tak način nam olajša računanje "na plus in minus", recimo:
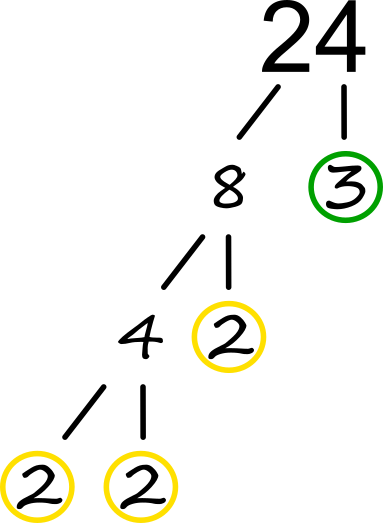
Število lahko zapišemo tudi v obliki prafaktorjev. Pri nas razcep števila na prafaktorje v šolah običajno učijo na način z navpično črto (nekajkrat smo ga uporabili tudi v naših video vsebinah), v tujini pa se ga lotijo tudi takole (angl. izraz "factor tree"): Razcep izvajamo s postopnim "drobljenjem" števila, na podlagi poznavanja poštevanke. Za 24 vemo, da je 8 krat 3. 3 je že praštevilo, zato se tu veja konča, 8 pa delimo naprej, vse dokler ne pridemo še do preostalih prafaktorjev. Drevo bi lahko npr. začeli tudi s "6 krat 4"; v tem primeru bi bila struktura drevesa drugačna, na koncu pa bi dobili iste prafaktorje kot na zgornji sliki. Predstavitev števila na tak način nam olajša računanje "na krat in deljeno" ter še kar nekaj drugih računskih operacij, ki iz omenjenega izhajajo, recimo:
S pomočjo praštevilske faktorizacije si močno poenostavimo tudi iskanje najmanjšega skupnega večkratnika, največjega skupnega delitelja ter najmanjšega skupnega imenovalca ulomkov. Če združimo tako zapis v obliki desetiških enot kot razcep na prafaktorje, pa si lahko pomagamo tudi pri računskih izrazih in deljenju z ostankom. Za boljšo preglednost in ločevanje vrst dreves se dogovorimo še za označevanje:
Omenjeno znanje nam pomaga tudi pri računanju na pamet, ki je ob hitrem preverjanju pravilnosti rezultatov na koncu pisnih testov praktično nepogrešljivo. Oglejmo si nekaj primerov tovrstnega računanja. Seštevanje brez prehoda Na podlagi drevesnega zapisa hitro ugotovimo:
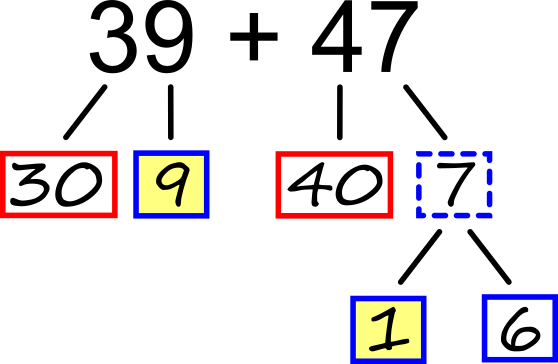
Seštevanje s prehodom Desetice enostavno seštejemo:
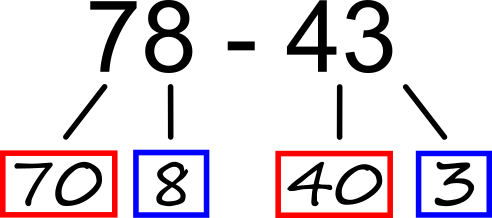
V našem primeru smo si ogledali prehod čez desetico. Na podoben način bi si lahko pomagali tudi pri prehodu čez stotico, tisočico ... Odštevanje brez prehoda Na podlagi drevesnega zapisa hitro ugotovimo:
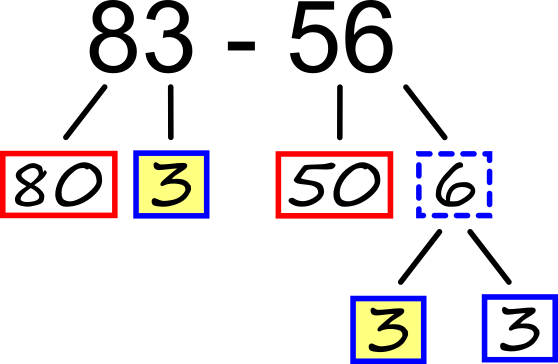
Odštevanje s prehodom Če ne bi imeli prehoda, bi preprosto odšteli desetice in enice, tako kot v prejšnjem primeru. A Ker računa "3 - 6" v okviru naravnih števil ne moremo izračunati, smo enico odštevanca (6) razdelili še naprej in sicer tako, da se del le-te ujema z enico zmanjševanca (3, obarvano rumeno). Račun nato izračunamo postopoma:
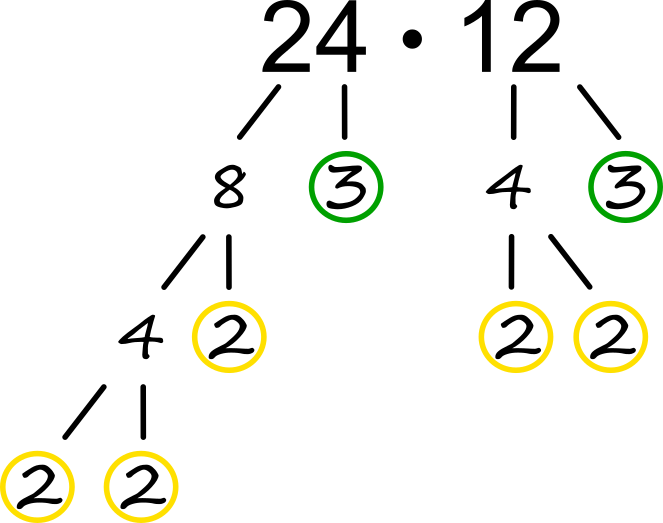
Dodatek: Če nalogo razširimo na cela števila, si lahko pomagamo s "trikom", ki je razložen tule. Množenje Če oba faktorja razcepimo na prafaktorje, rezultat lahko preprosto zapišemo v obliki potenc:
Rezultat lahko razmeroma hitro dobimo tudi z množenjem praštevil, kjer upoštevamo:
V našem primeru bi tako izračunali:
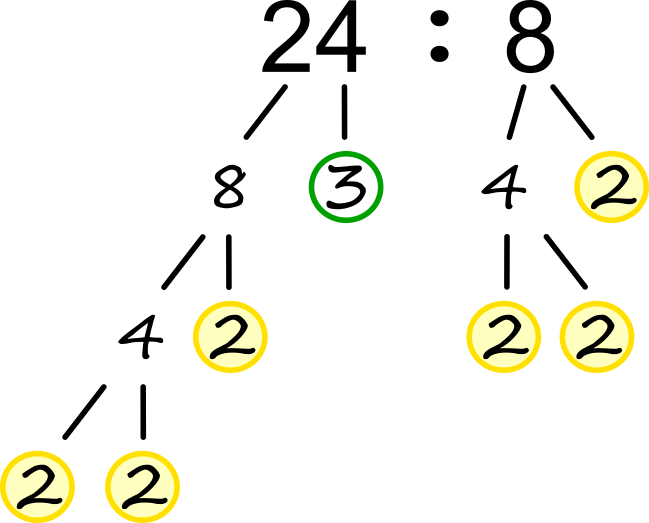
Do rezultata seveda lahko pridemo tudi s pisnim množenjem, kjer pa si s številskimi drevesi lahko pomagamo le v manjši meri. Deljenje Tako kot smo pri odštevanju ločeno odšteli desetice in enice, lahko pri deljenju enako storimo s prafaktorji, ki smo jih dobili s praštevilskim razcepom deljenca (24) in delitelja (8), saj je koncept odštevanja in deljenja zelo podoben. Račun izračunamo postopoma:
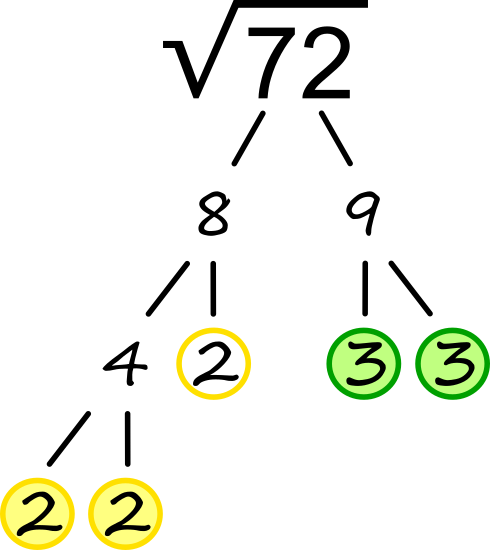
Za razmislek: Ob upoštevanju, da je deljenje je isto kot krajšanje ulomkov, s pomočjo številskih dreves skušaj okrajšati ulomek 24/8. Delno korenjenje Če število pod korenom razcepimo na prafaktorje, ga lahko zapišemo v obliki potenc:
Končni rezultat je torej: √72 = √2²∙2∙3² = 2∙3√2 Pod korenom je ostal prafaktor 2, ker "nima svojega para". 20 + ☐ - 10 = 40
Saj poznate tale tip naloge, kajne? :) Kako najlažje ugotoviti, kaj je potrebno vpisati v okvirček? Enačaj nam pri tem lahko močno pomaga. Kaj pomeni "je enako"? Dobesedno pomeni "je enako" :) In kaj je enako? Seštevek števil na levi in na desni. No, na desni nam niti računati ni potrebno, ker imamo le eno število :) Opomba: govora je o seštevku, števil na levi strani. Zraven seveda štejemo tudi odštevanje, ki je v bistvu prištevanje nasprotnih števil. Računali bomo torej le na levi strani. Zapišimo levo stran računa še "v barvah", da bo lažje razumljiv: 20 + ☐ - 10 = 40 Pri "barvanju" smo upoštevali, da znak za računsko operacijo vpliva na število, ki mu sledi (na desni) in ne na število pred njim oziroma (na levi). Več o tem si lahko preberete tule. Ljudje smo (večinoma) narejeni tako, da se najprej lotimo tistega, kar poznamo, šele nato pa neznanega. Tudi tu bomo naredili tako. Komur okvirček ni všeč, račun lahko zapiše tudi takole: 20 + ? - 10 = 40 "Naberimo" torej na levi strani skupaj tisto, kar poznamo ... 20 - 10 ... in izračunajmo: 20 - 10 = 10 Kaj nam je torej do sedaj uspelo narediti? Na levi strani smo združili znano in dobili: 10 + ☐ = 40 Tole je pa že kanček lažje, kajne? :) Zopet se spomnimo na enačaj, ki nam pove, da mora biti rezultat na levi strani enak rezultatu na desni. Če imamo na levi strani 10, na desni pa 40, nam na levi nekaj manjka. Koliko moramo torej dodati na levi strani, da dobimo isto, kot imamo na desni? Odgovor je 30, saj velja 10 + 30 = 40 Opomba: Sklepali bi lahko tudi, da imamo na desni strani 30 preveč, kar je sicer pravilno, a potem računa ne bi mogli rešiti, saj se okvirček nahaja na levi in ne na desni strani. V okvirček tako zapišemo 30 in celoten račun se glasi: 20 + 30 - 10 = 40 Če naredimo preizkus, na levi strani res dobimo 40. Še nasvet za konec: Namesto (abstraktnih) števil lahko pri enačenju uporabimo tudi konkretne pripomočke - štejemo kocke, kroglice, denar ... ali pa tehtamo. |
ARHIV
May 2024
KATEGORIJE
All
|


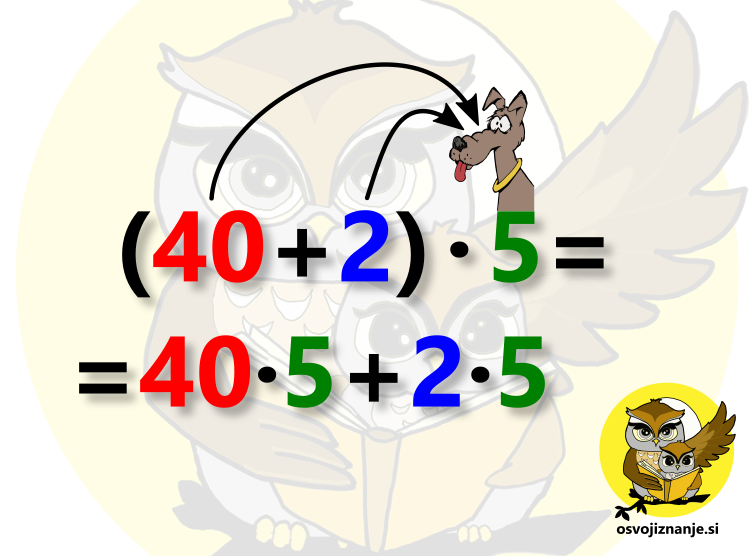
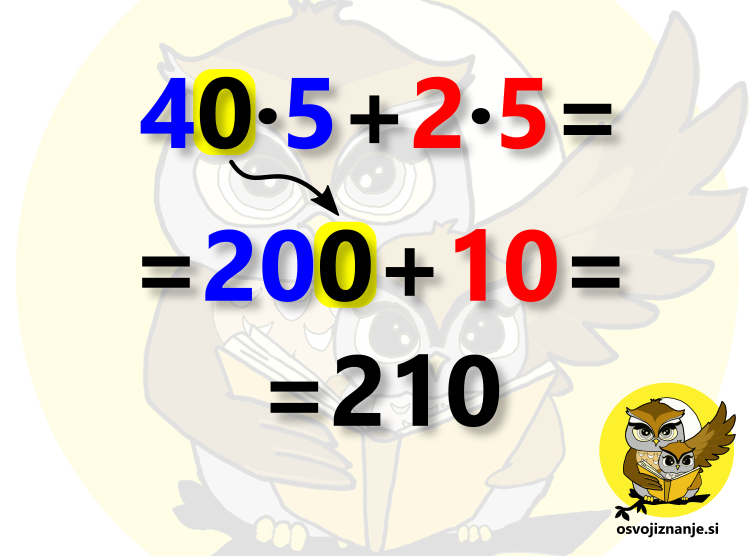







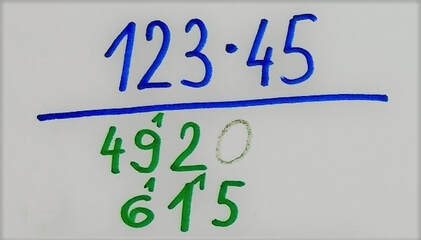
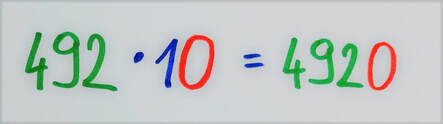
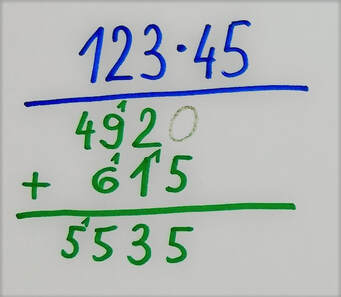
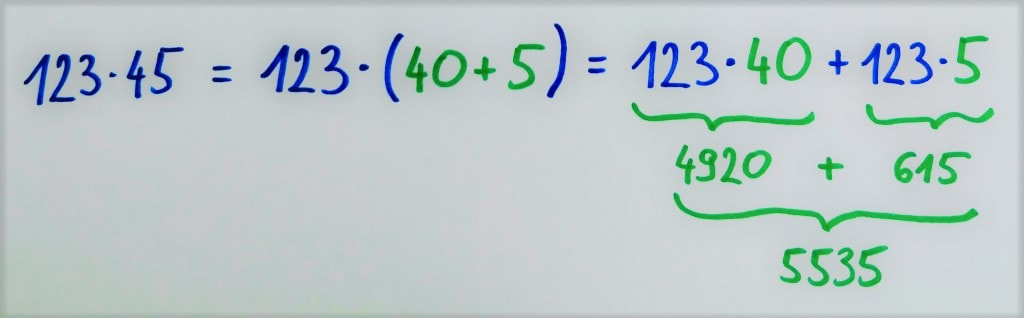
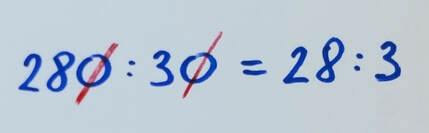



 RSS Feed
RSS Feed
