Za plus in minus trakci, za krat in deljeno ploščice

Vedno bolj se zavedamo, da je vizualizacija zelo pomembna za razumevanje matematičnih zakonitosti. Pa tudi kakšnih drugih. Ampak, ostanimo zaenkrat pri matematiki. Konkretneje, pri osnovnih računskih operacijah.

Načinov za vizualno predstavitev seštevanja, odštevanja, množenja in deljenja je kar veliko, zato smo včasih v dilemi, katerega uporabiti. Seveda je najbolje, da si vsakdo izbere takega, ki ustreza prav njemu, a vseeno je nekje potrebno začeti.  ;)

Sam ponavadi začnem z dvema modeloma oziroma didaktičnima pripomočkoma (če ju imamo na voljo v fizični obliki), to sta:

• trak za seštevanje in odštevanje ter
• ploščice za množenje in deljenje.

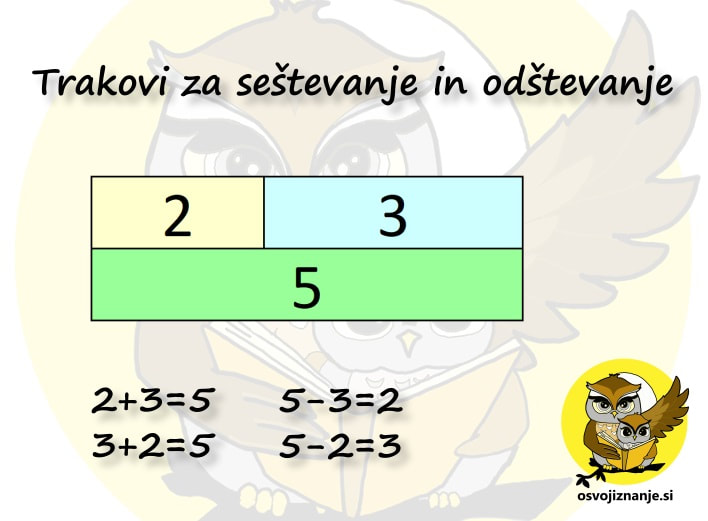
Glavna razlika med trakom in ploščicami je dimenzija. Trak se razteza le v eni smeri, medtem ko je polje ploščic dvodimenzionalno.

Če trakove zlagamo enega za drugim, nam celotna dolžina take »kače« predstavlja vsoto posameznih trakov, s čimer ponazorimo seštevanje. Če trakove zlagamo vzporedno, pa jih med seboj lahko primerjamo. Se sprašujete, kje smo izgubili odštevanje? ;) Odštevanje najlažje ponazorimo z razliko med dolžinama dveh trakov.

Kljub temu, da ne govorim o merjenju, ampak o računanju, sem že dvakrat omenil dolžino. Malo iz navade, malo pa nalašč. ;) Seštevanje in odštevanje si namreč v naravi najlažje predstavljamo prav z merjenjem razdalje. Če na primer najprej prehodim 3 kilometre, nato pa še 2, sem skupaj prehodil 3+2, torej 5 kilometrov (seštevanje, vsota). Če je sosednja vas oddaljena 6 kilometrov, pa moram do nje prehoditi še 6-5, torej 1 kilometer (odštevanje, razlika).

Kaj pa množenje in deljenje? Za množenje vemo, da predstavlja seštevanje več enakih števil hkrati, lahko bi mu rekli tudi »turbo seštevanje«. :) Zakaj bi recimo preštevali 56 rozin, ko pa jih lahko zložimo v 7 vrstic po 8 ali 8 vrstic po 7 rozin? Ja, 7 krat 8 je isto kot 8 krat 7, le gledamo nekoliko z druge perspektive. In ja, govorimo o poštevanki. :) Poštevanka ni nič drugega kot vsi možni računi množenja s faktorji od 1 do 10. In če želimo pri računanju imeti »doživljenjski turbo pogon«, se jo je dobro dobro naučiti. Ja, dobro je zapisano dvakrat, ne gre za slovnično napako. :)

Pri deljenju pa imamo prav tako opravka z več enakimi števili, le da jih tu ne seštevamo, ampak neko večje število razdelimo na več enakih manjših števil.

Včasih to (v množici celih števil) ni mogoče, zato govorimo o deljenju z ostankom. Pri deljenju z ostankom eno od števil vedno »nasrka«, saj je manjše od ostalih. Saj poznate tisto, trije starejši bratje in četrti »mulc«, ki je komaj iz plenic ... nikoli nima prav. ;)

Glede na povedano množenje torej najlažje predstavimo z zlaganjem v stolpce in vrstice. Kaj pa bi zlagali? Ploščice. Ali, če želite, polagali, tako kot tiste v kopalnici. ;) Z deljenjem pa te ploščice razdelimo, podolgem ali počez.