|
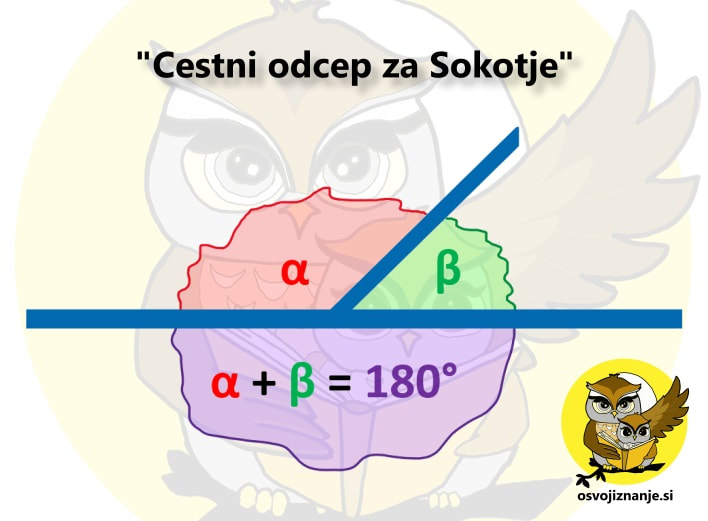
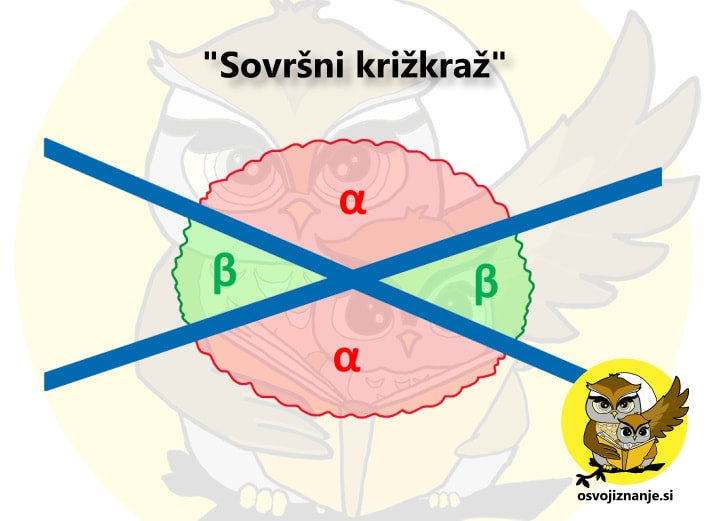
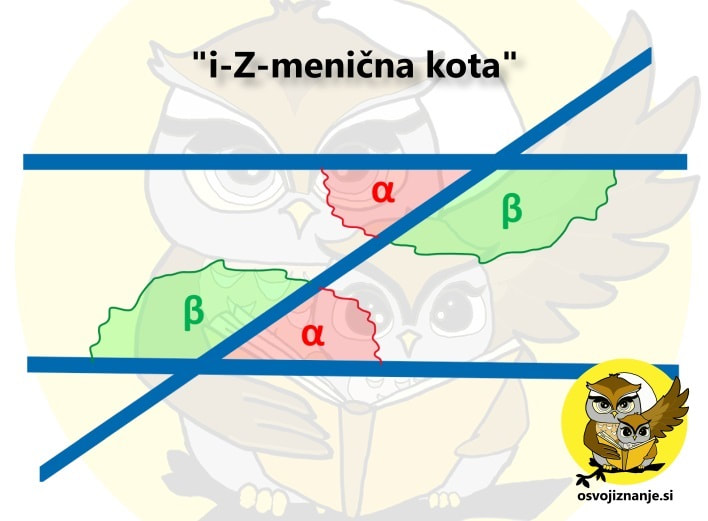
Koti radi nastopajo v paru, tudi v matematičnih testih. ;) Kdaj sta kota sokota in kdaj sovršna kota? Kaj pa izmenična kota? Čeprav se sliši zakomplicirano, si pojme zapomnimo veliko lažje, če si jih predstavljamo vizualno, zraven pa pripišemo še kakšno besedno zvezo. Temu se strokovno reče "dvojno kodiranje" (več o metodi učenja si lahko preberete v našem slovarčku). Mi imamo za vas nekaj predlogov, izmislite pa si seveda lahko tudi svoje. Ko govorimo o sokotih, si lahko predstavljamo ravno cesto z odcepom: Za sokota je značilno tudi to, da si delita en krak. No, ta krak je v našem primeru cestni krak :). Pri učenju sovršnih kotov si lahko predstavljamo »križkraž« ali črko x: Za sovršna kota je značilno tudi to, da si delita vrh, na kar lahko sklepamo že iz imena samega. Če seveda vemo, kaj je vrh kota. ;) Tudi tu se lahko znajdemo - če sta kraka nogi, je vrh kota lahko glava (saj se spomnite »glavonožcev«, ki smo jih risali v vrtcu? :) Pri izmeničnih kotih pa si zopet lahko pomagamo z abecedo, to je lahko črka Z ali pa črka N (kot nalašč obe najdemo tudi v imenu - iZmeNična kota): Ob pozornem pogledu na zadnjo sliko pa lahko opazimo tako sokote kot tudi sovršne kote. Kot je matematiki že običaj, je tudi tu vse povezano med seboj.
Zato kot že mnogokrat - ne učimo se matematike na pamet, ampak - po pameti! ;)
0 Comments
Pravijo, da slika pove več kot 1000 besed: Že res, ampak tule vam vseeno malo pomagam. ;)
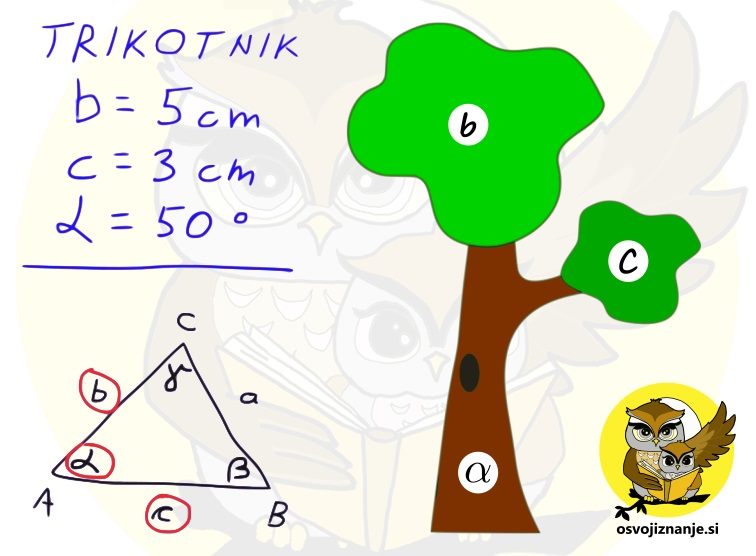
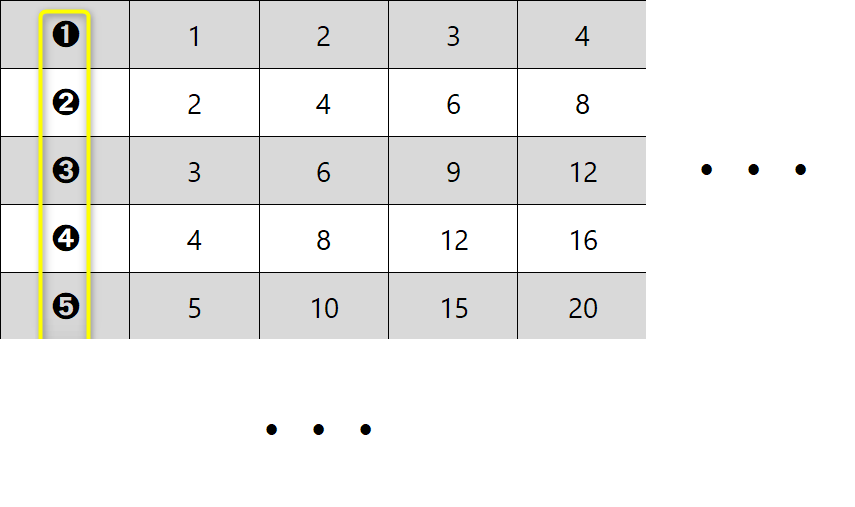
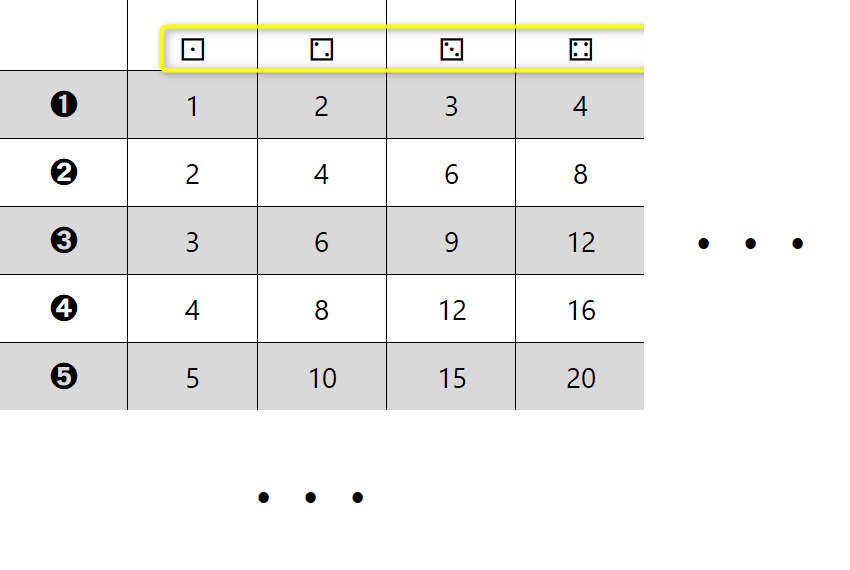
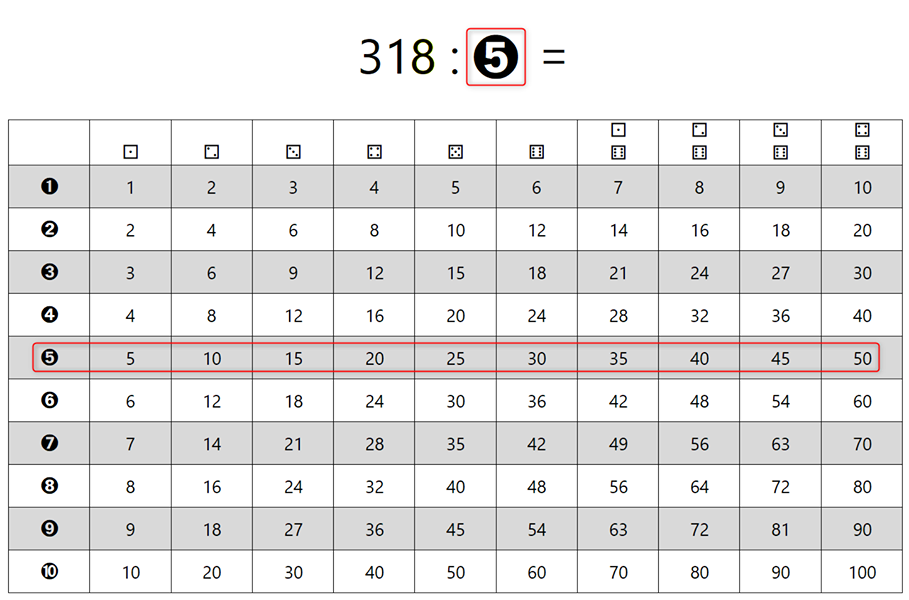
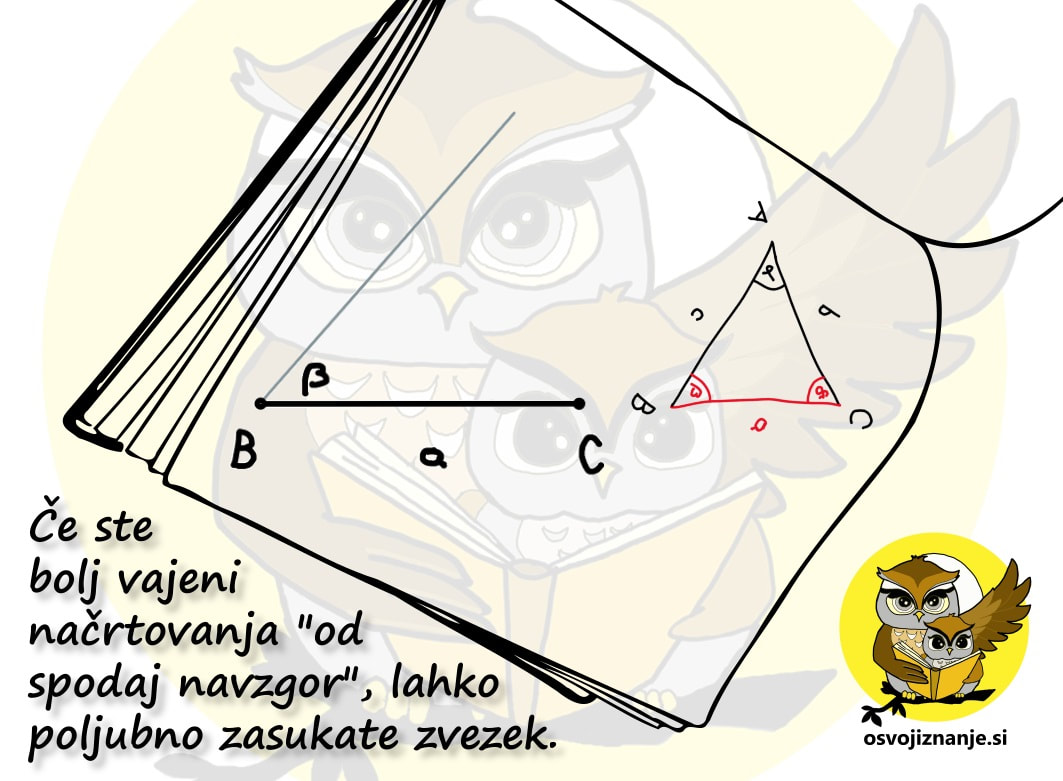
Slika predstavlja dokaj enostavni "recept" za načrtovanje geometrijskih likov, ki se glasi: "Najprej narišemo tisto, kar je vmes, nato pa še tisto, kar je na levi in na desni strani." V našem primeru pri trikotniku najprej narišemo kot alfa, nato pa na njem odmerimo še stranici c in b. "Logiko" si lahko zapomnimo s pomočjo drevesa. če hočemo priti do krošnje, moramo najprej splezati po deblu. ;) Naj vas najprej pomirim, tale pripomoček ni "potuha", če se je kdo slučajno ustrašil, je pa odličen "pomočnik" pri deljenju z ostankom in nam omogoča, da postopek tudi dejansko razumemo, ne le "znamo na pamet", kakor je na žalost dokaj pogosto pri poštevanki. Za 4 krat 5 vemo, da je 20, 20 deljeno s 4 pa je že problem. Kaj šele 21 deljeno s 4 ... Pri deljenju je ključno poznavanje večkratnikov delitelja (to je število, s katerim delimo oz. "tisto, kar stoji za dvopičjem" 😉). Zato celoten pripomoček temelji na večkratnikih števil. Zapišimo prvih 10 večkratnikov števil od 1 do 10 in sicer za vsako število v svojo vrstico tabele: Verjetno se vsi strinjamo, da se matematične pojme in postopke lažje zapomnimo, če jih povežemo z nečim znanim iz življenja. Nekaj takšnega so igralne kocke. Kot vemo, število pik pomeni vrednost, ki je "padla" ob metu kocke. Ena pika pomeni eno točko. Sedaj pa si predstavljajmo, da pika ni vredna eno točko, ampak več točk, od 1 do 10. To označimo tudi na naši tabeli - v prvi vrstici je pika vredna eno točko, v drugi dve in tako naprej do 10: Imena vrstic smo označili, preostanejo pa nam še imena stolpcev. Na podoben način, kot smo s številkami od 1 do 10 v krožcih označili vrstice, označimo tudi stolpce in sicer s kockami, na katerih je "padla" vrednost od 1 do 10. Ko na eni kocki "zmanjka pik", dodamo še eno kocko. Število pik na kocki pomeni, kateri večkratnik (po vrsti) števila v krožcu (v računu bo to delitelj) je zapisan v stolpcu pod kocko. Da bo razumevanje lažje, dodajmo še primer. Če na kocki padejo 4 pike (skrajno desni stolpec na sliki) in je vrednost posamezne pike 5 (spodnja vrstica na sliki), je skupna vrednost vseh pik 20, saj je 4 krat 5 enako 20. Velja seveda tudi, da je 20 deljeno s 4 enako 5 in 20 deljeno s 5 enako 4. Sedaj pa si oglejmo uporabo pripomočka na konkretnem računu deljenja z enomestnim številom, izračunajmo, koliko je 318 : 5. Ker delitelj (5) deli deljenca (318), bo iz deljenca nastalo več (enako velikih!) delčkov (in še nekaj ostanka). Število teh delčkov bomo zapisali desno od enačaja (to pa bo količnik). En tak delček je "vreden" 5 enot, ravno toliko, kot je "vreden" delitelj. "Po domače" nas zanima, koliko "petic" lahko "stlačimo" v škatlo, v katerem je prostora za 318 enot. Do rezultata najlažje pridemo tako, da poiščemo večkratnike delitelja, v našem primeru 5: Ker je 318 kar veliko število, bi morala biti spodnja tabela zelo široka, da bi v njej lahko našli rezultat. 🙂 Zato se reševanja lotimo postopoma. V vsakem koraku se bomo osredotočili le na prvih devet večkratnikov delitelja (dopustimo tudi 0), zato bo tabela z desetimi stolpci popolnoma dovolj. S tem postopkom v vsakem koraku dobimo eno števko rezultata oziroma količnika. Ker bomo račun reševali postopoma, je na začetku potrebno določiti, kolikšen del deljenca (318) bomo uporabili v prvem koraku. Izbiro začnemo z leve strani. Ker je vrednost prve števke (3) manj od 5 (delitelj), vzamemo prvi dve števki oziroma število 31. To število podčrtamo z vodoravno črto. Nadaljnji postopek pa je popolnoma enostaven:
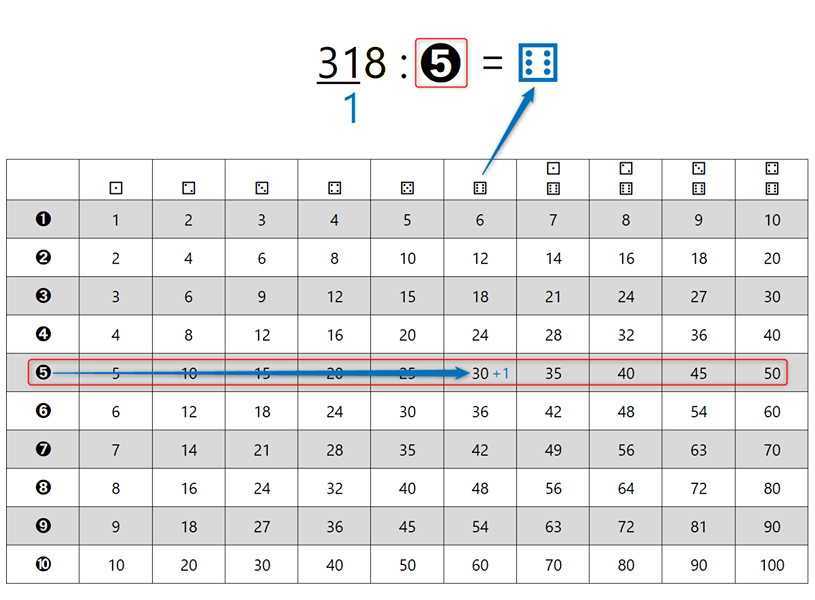
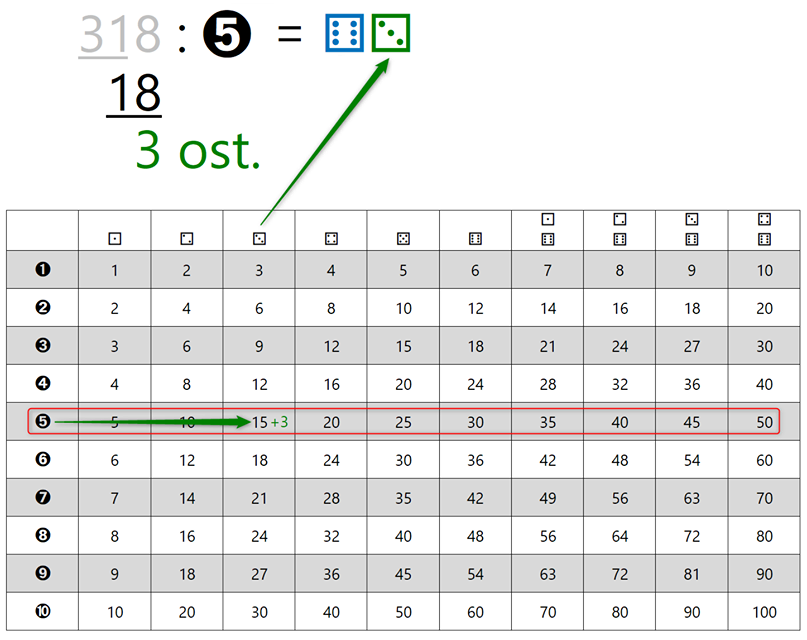
Do sem je postopek dokaj standarden (morda le z izjemo načina označevanja stolpcev in vrstic v tabeli), medtem ko je naslednja ideja nekoliko bolj "smela". Pri prehodu na naslednji korak je potrebno določiti naslednji "mini" deljenec (v prejšnjem koraku je bilo to število 31 oziroma število, sestavljeno iz levih dveh števk števila 318). Običajno k ostanku v vrstici pod vodoravno črto (v našem primeru je to 1) prepišemo prvo števko od leve proti desni, ki ni podčrtana (v našem primeru je to 8) in dobimo naslednji "mini" deljenec 18. Naš predlog, ki bi si ga učenci verjetno lažje zapomnili, je naslednji: zakaj ne bi k ostanku v vrstici pod vodoravno črto "potisnili" kar celoten preostanek števila, ki ni podčrtan? V našem primeru je to sicer le števka 8, ampak če bi bil deljenec "daljši", bi pa lahko navzdol prestavili kar vse, kar ni podčrtano (trik: za lažje pomnjenje bi si predstavljali, da je delu deljenca "zmanjkalo tal pod nogami" 🙂 - to asociacijo bi si učenci lahko priklicali v spomin tudi, če bi postopek že nekoliko pozabili) S predlaganim pristopom je sicer v naslednjem koraku (in vsem, ki mu potencialno sledijo) potrebno znova določiti "mini" deljenca, a to ne bi smel biti prevelik problem saj za vse korake uporabimo enako logiko določevanja le-tega. Ponovimo postopek še za drugi "mini" deljenec (v našem primeru je to 18):
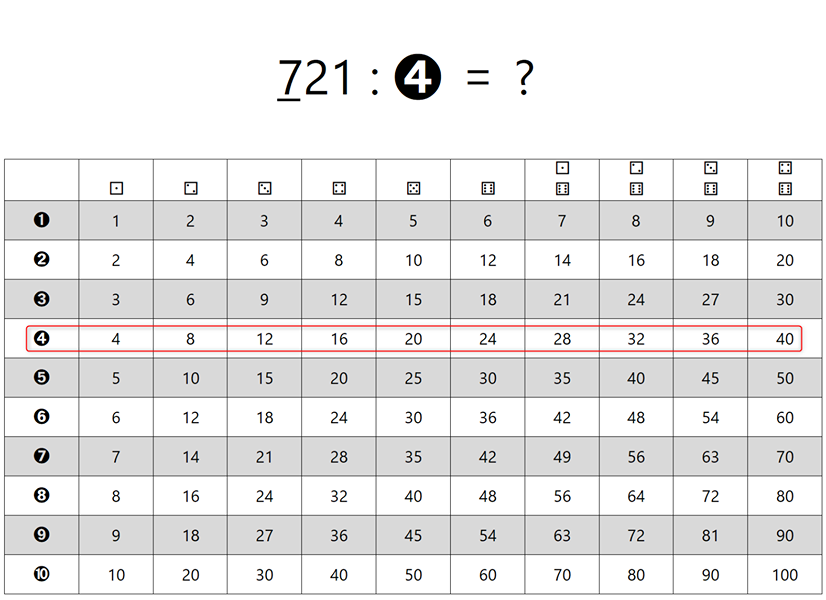
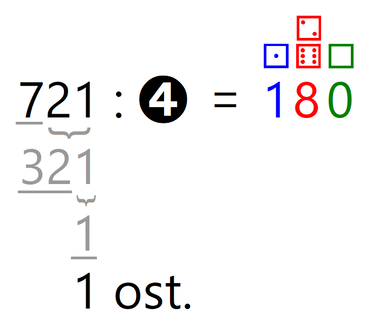
Ker desno od vodoravne črte ni nobene števke več (podčrtano je celotno število, s katerim smo delili oz. celoten "mini" deljenec, to je 18, zato nobeni števki ne more "zmanjkati tal pod nogami" 😉), smo z računanjem zaključili. Ostanek, ki smo ga dobili v zadnjem koraku deljenja (v našem primeru je to 3), je končni ostanek pri deljenju. Tega moramo v testu zapisati k rezultatu deljenja oziroma količniku, ki ga bomo iz kock "prebrali" pri zapisu končnega rezultata. Zapišimo še končni rezultat. Ostanek smo že določili, sedaj le še "preberimo" vrednosti kock. Število pik na kocki predstavlja vrednost posamezne števke, v našem primeru sta to 6 in 3, kar predstavlja število 63. V našem primeru, kjer smo število 318 delili s številom 5, smo torej dobili količnik 63 ter ostanek 3. Z drugimi besedami, v število 318 lahko "stlačimo" 63 petic, pa še ostane prostor za tri "vitke" enice. 😉 Naloga Izračunaj, koliko je 721 : 4. V tabeli je že označen "namig": Rešitev:
V našem primeru je druga vrstica nekoliko drugačna od tistega, kar se običajno uči v šolah (iz prve vrstice bi se namreč v drugo vrstico poleg ostanka 3 "morala po pravilih" prenesti le dvojka, ne pa celoten preostanek deljenca).
Pravilo sem nekoliko priredil, ker menim, da se učenci postopek lažje zapomnijo, če si predstavljajo, da preostanek števila, ki ni podčrtan, "pade v spodnje nadstropje" :) Kljub "mini spremembi" račun ni napačen, le potrebno je paziti, da v vsaki vrstici podčrtamo nov "vmesni deljenec", kar v "originalnem" postopku ni potrebno. Mogoče nekoliko razmišljanja več, a koraki so s tem poenoteni, kar pa tudi prispeva k lažji razumljivosti. Pazljivost je potrebna edinole v primerih, kjer pri deljenju vmesnega deljenca ni ostanka. Če v koraku, ki sledi, podčrtamo dve števki, je v rezultat potrebno "vriniti" še eno ničlo. Primer: 18300 : 6. Zakaj pa ne? :) Sicer ne dobesedno, ampak zavoj toast kruha je tako "matematičen", da grem težko mimo njega ;) Na njem si oglejmo nekaj količinskih predstav. Zamislimo si, da zavoj z desetimi rezinami kruha predstavlja tisočico. Če celotni zavoj kruha predstavlja tisočico, ena izmed rezin predstavlja desetino celotnega zavoja oziroma stotico. Tako kot deset rezin predstavlja celoten zavoj, deset stotic predstavlja eno tisočico. Mali otroci imajo radi kruh, narezan na "vojačke". En tak "vojaček" predstavlja desetino celotne rezine oziroma desetico. Tako kot deset "vojačkov" predstavlja celotno rezino, deset desetic predstavlja eno stotico. Kockice suhega kruha se odlično priležejo v juhi. Ena taka kockica predstavlja desetino "vojačka" oziroma enico. Tako kot deset kockic predstavlja celotnega "vojačka", deset enic predstavlja eno desetico. Raziskave kažejo, da si matematiko si najbolje zapomnimo na podlagi praktičnih primerov, zato pozorno opazujmo naravo okoli sebe in sigurno bomo našli še kaj uporabnega za naslednjo uro matematike. ;)
Pri razstavljanju izrazov moramo biti dobri opazovalci, da pravilno »identificiramo« zapis, na podlagi česar se potem odločimo za postopek. Seveda obstaja lažji način od učenja vseh kombinacij na pamet, ampak ga včasih učitelji niso veseli. Je pa z njim vseeno možno rešiti kakšno nalogo več. Omejimo se na dvočlenike, ki jih obravnavamo v osnovni šoli. Najprej je seveda potrebno vedeti, ali izraz razstavljamo ali poenostavljamo. Pri nalogi običajno jasno piše, še vedno pa je dobro »od daleč« videti, kaj bomo počeli: Poenostavljeno povedano: zgornji izraz na sliki nima oklepajev, zato ga je potrebno razstaviti, spodnji pa ima oklepaje, zato pri njem pride v poštev poenostavljanje. V nadaljevanju se posvetimo razstavljanju. Pri tem imamo v bistvu le dve večji opciji – izpostavljanje skupnega faktorja ali pa Vietovo pravilo: Oba izraza na zgornji sliki imata tri člene, ampak zgornji ima v prvem členu številski faktor, poleg tega pa ima še različne črke (spremenljivke), medtem ko gre desni po pravilu »spremenljivka na kvadrat, spremenljivka, brez spremenljivke« (govorimo o spremenljivki a na sliki). Zato prvega rešimo z izpostavljanjem skupnega faktorja, drugega pa po Vietovem pravilu. Se sprašujete, kam sta izginila kvadrat dvočlenika ter produkt vsote in razlike? Brez panike, tudi ta dva tipa razstavljanja si bomo ogledali, jima pa ne bomo dodelili svojega postopka, saj ju je moč rešiti s pomočjo vietovega pravila. V šoli vam pa tega običajno ne povedo, ampak vas naučijo še dva postopka, kot da jih že tako ali tako ni dovolj ... Najprej si oglejmo prvi »posebni primer«: Veste, kateri izraz na zgornji sliki predstavlja kvadrat dvočlenika? V bistvu vam sploh ni treba vedeti. Izraz ustreza »normam« za razstavljanje po Vietovem pravilu, torej ga ne bomo reševali z izpostavljanjem skupnega faktorja. Če bomo kot rezultat dobili dva popolnoma identična faktorja, ju bomo zapisali kot kvadrat, sicer pa enega zraven drugega. Sedaj pa si oglejmo še situacijo s produktom vsote in razlike: Če med prvi in drugi člen spodnjega izraza zapišemo »0⋅a«, se vrednost izraza ne spremeni, nova oblika pa je ustrezna za razstavljanje po Vietovem pravilu:
a² + 0⋅a – 9 Razstavljanje marsikomu povzroča kar nekaj težav, a ni potrebno, da je tako. Predvsem se ga ne smemo ustrašiti in tudi če pozabimo kakšno pravilo, imejmo v mislih, da se vedno lahko znajdemo in z nekaj logike račun rešimo nekoliko drugače. Vemo, da je število deljivo z 2, če se konča z 2, 4, 6, 8 ali 0 ter deljivo s 5, če se konča z 0 ali 5.
Potem pa so tu »naloge z zvezdico«, kjer se naučimo še, da je število deljivo s 4, če sta s 4 deljivi zadnji dve števki oziroma deljivo s 25, če sta s 25 deljivi zadnji dve števki. V primeru, da sta zadnji dve števki enaki 0, je število deljivo tako s 4 kot s 25. Največji ljubitelji matematike se potem naučijo še to, da je število deljivo z 8, če so z 8 deljive zadnje tri števke. Prepoznate vzorec? Pri deljivosti s katerim številom si še lahko pomagamo z zadnjimi tremi števkami? Vrnimo se k deljivosti z 2 in 5. Če pravilo zapišemo podobno kot pravilo za deljivost s 4 in 25, se glasi: Število deljivo z 2, če je z 2 deljiva zadnja števka oziroma deljivo s 5, če je zadnja števka deljiva s 5. Pozabiti pa seveda ne smemo na primer, ko je enica enaka 0. V tem primeru je število deljivo tako z 2 kot s 5. Po tej analogiji bi moralo obstajati še eno število, pri deljivosti s katerim si lahko pomagamo z zadnjimi tremi števkami. Kako ga lahko ugotovimo? Zopet se vrnimo k deljivosti z 2 in 5. Če štejemo naprej po večkratnikih števila 2, se vsak vzorec konča z 0 na mestu enic. Enako velja za štetje po večkratnikih števila 5. Zato je dovolj za deljivost gledati le zadnjo števko. Če štejemo po večkratnikih števila 4, pa se vsak vzorec konča z »00« na mestu desetic in enic. Enako velja za večkratnike števila 25. Zato moramo za deljivost gledati zadnji dve števki. Enako velja za večkratnike števila 8. Tu se vsak vzorec konča z »000« na zadnjih treh mestih. Vse lepo in prav, a še vedno ne vemo, pri deljivosti s katerim številom si še lahko pomagamo z zadnjimi tremi števkami. Pomislimo, kakšna povezava obstaja med 2, 5 in 0 na mestu enic. Kaj pa med 4, 25 in »00« na mestu desetice in enice? 2 ∙ 5 je 10, 4 ∙ 25 pa je 100. 4 ∙ 25 lahko zapišemo tudi kot 2² ∙ 5² oziroma (2 ∙ 5)². Naš odgovor je že skoraj na dlani. Koliko krat 8 je 1000? Oziroma koliko na tretjo potenco krat 2³ je 1000? Po dosedanji logiki 5 na tretjo potenco oziroma 125. Res je, 125 ∙ 8 = (5 ∙ 2)³ = 1000 in število je deljivo s 125, so s 125 deljive zadnje tri števke. Ne verjamete? Poizkusite s kalkulatorjem in enim zelo velikim številom, recimo 45653454243443375:125. Ni važno, kako veliko je število, pomembne so samo zadnje tri števke. Za konec pa še vprašanje. Deljivost s katerimi števili lahko še raziščemo na podlagi ugotovljenega? Kaj ima seštevanje in odštevanje v okviru celih števil skupnega s košarko?
Predstavljajmo si tekmo med plusi in minusi in ves čas spremljajmo razliko v rezultatu:
3 -2 -2 +1 -3 +2 Kakšen je torej trenutni rezultat?
Tudi rezultat računa 3 -2 -2 +1 -3 +2 je enak -1. Minus 1, ker "minusi vodijo za 1 točko". V nižjih razredih osnovne šole učenci še ne obvladajo "obračanja enačb", zato tako enačbe kot neenačbe rešujejo s poskušanjem. Pri enostavnih enačbah to nekako še gre, pri neenačbah pa se zadeva lahko kaj hitro "zavleče". Zato je koristno pri tem uporabiti nekaj logičnega sklepanja. Oglejmo si primer reševanja neenačbe x+2>=5:
Rešitev neenačbe x+2>=5 je torej x>=3. Opomba: Opisana metoda je primerna za reševanje neenačb v okviru množice naravnih števil + števila 0. Na tak način lahko rešimo enačbe s seštevanjem in odštevanjem, pri enačbah z množenjem in deljenjem pa je potrebna previdnost, predvsem če ulomki še niso bili obravnavani. V poštev v tem primeru pridejo samo določene kombinacije števil. Če je omenjena metoda prezahtevna, lahko za začetek poskusimo s tabelo, v katero vnesemo števila od 1 do 10 kot potencialne rešitve in nato eno po eno preverjamo, če ustreza. Ob tem lahko s pomočjo elaboracije preidemo na prvotno opisano metodo. Tule je še nekaj primerov za vajo: x > 3 x <= 7 x+2 > 5 x-2 <= 6 2+x >= 4 7-x < 5 Ko imamo opravka s pozitivnimi števili, ponavadi ni težav, saj »smo z njimi gor rasli«. Pri negativnih številih pa si s »klasičnimi« modeli ne moremo več pomagati (predstavljajte si, da je na avtobusu 5 ljudi, nato pa jih 7 izstopi – mission impossible), zato si je potrebno izmisliti nove. Najdete jih na koncu tega članka, prej pa si odgovorimo še na nekaj vprašanj. Predznak ali računska operacija? Kadar množimo ali delimo, ni dileme: če se vmes pojavi kakšen plus ali minus, gre definitivno za predznak. Pri seštevanju in odštevanju pa zadeva postane že bolj zanimiva, a povsem obvladljiva, če upoštevamo naslednje:
Za predznak je logično, da je negativen, saj pozitivnega ni potrebno pisati, v nalogah pa je potrebna pazljivost, saj nikjer ne piše, da pozitivnega predznaka ne smemo pisati, zato nas učitelji radi presenetijo tudi s kakšnim zapisom v stilu »2+(+3)-(+5) ...« Zakaj moramo predznak postaviti v oklepaj? Zato, ker se z računsko operacijo »ne marata« in ju je potrebno fizično ločiti. :) Ne vem, če je to sicer res, si je pa lahko zapomniti. :) Povrhu zapis brez oklepaja še »grdo zgleda«, recimo 5 - - 3, 6 + - 2 ... Prišteti ali odšteti, to je sedaj vprašanje Ko se pred nami pojavi račun s samimi plusi in minusi, med katerimi je nekaj računskih operacij, nekaj pa predznakov, ga je potrebno najprej poenostaviti, kar marsikomu povzroča težave. Zato sem za vas pripravil nekaj modelov, s katerimi si lahko pomagate. Če si predstavljamo, da računski operaciji seštevanja in odštevanja pomenita segrevanje in ohlajanje, predznak minus pa zanikanje trditve in zamižimo na eno oko glede slovnice, rezultat dobimo že z nekaj logike: Na podoben način si seštevanje in odštevanje lahko predstavljamo kot hojo naprej in nazaj po sobi, pri čemer nas negativni predznak obrne za 180 stopinj: Lahko pa rečemo, da je število s predznakom minus »negativno razpoloženo« in računski operaciji, ki stoji pred njim, »meša štrene« in sicer tako, da plus spremeni v minus, minus pa v plus. :)
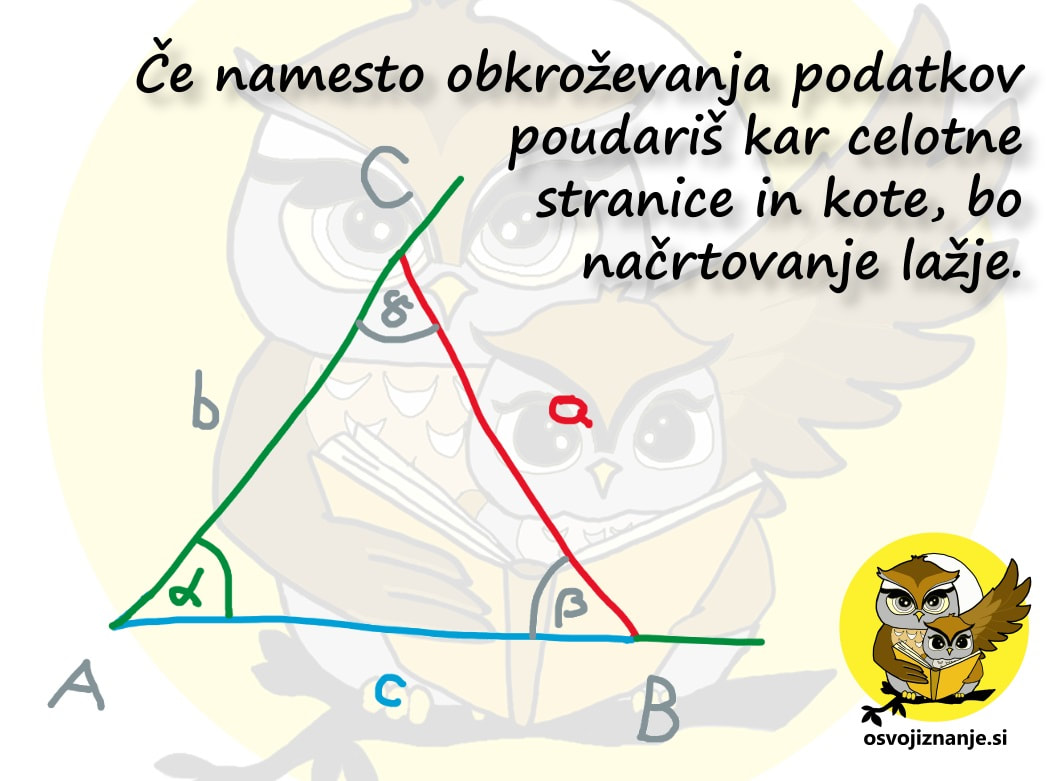
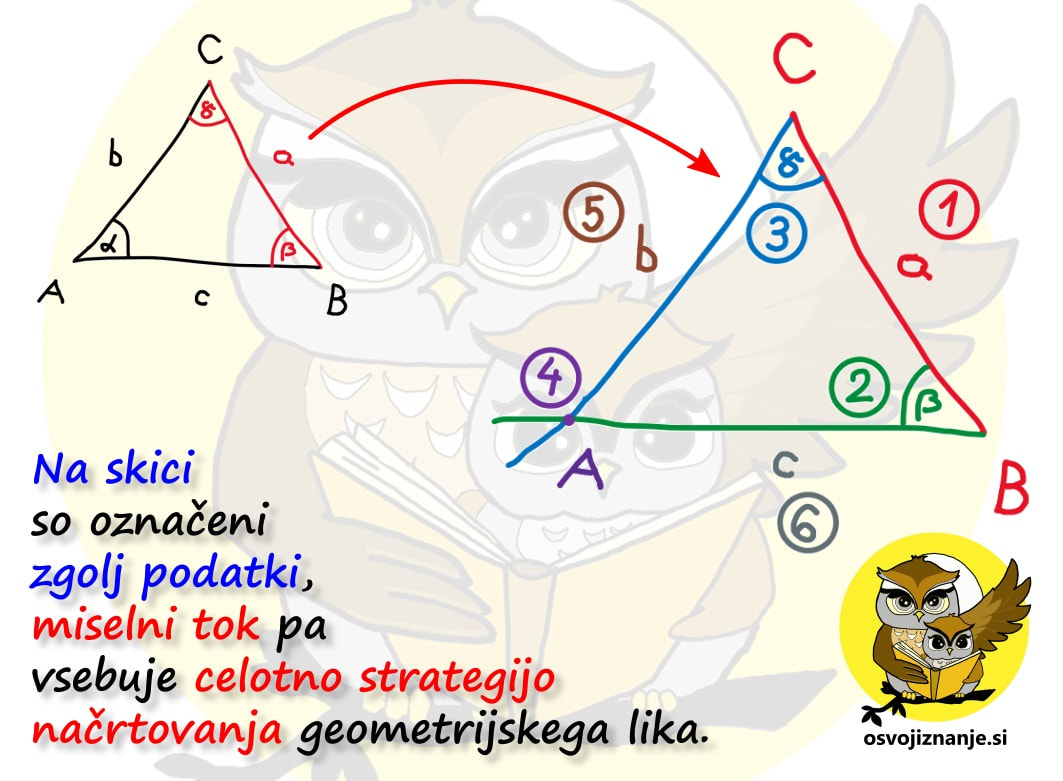
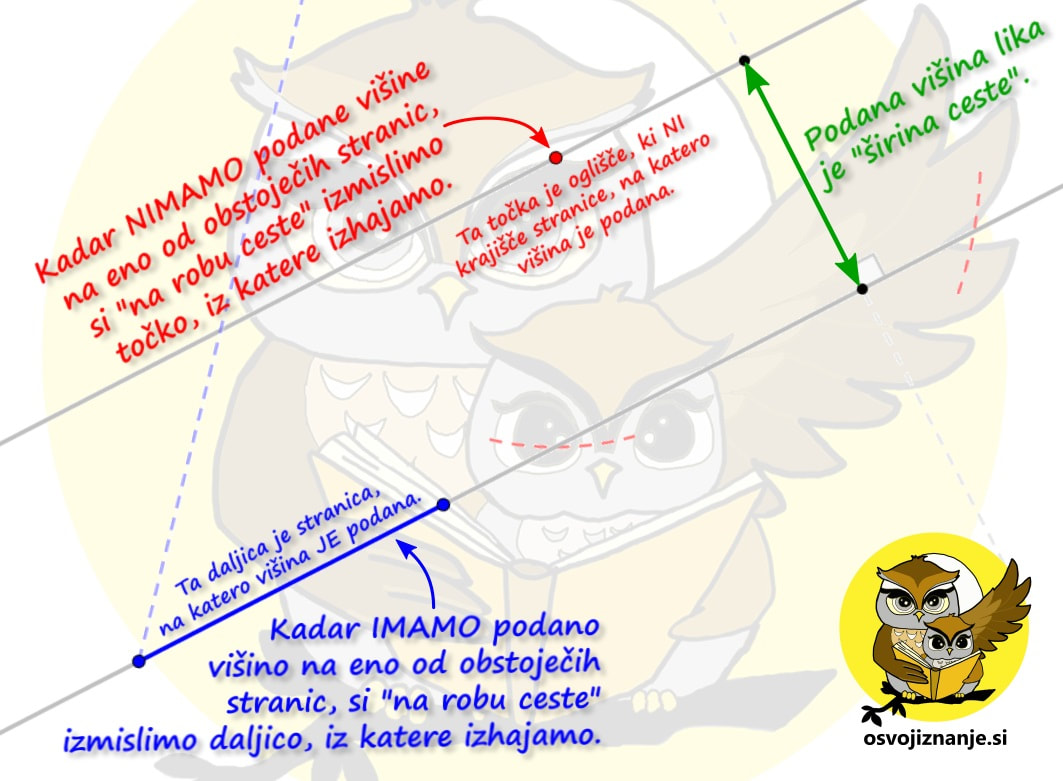
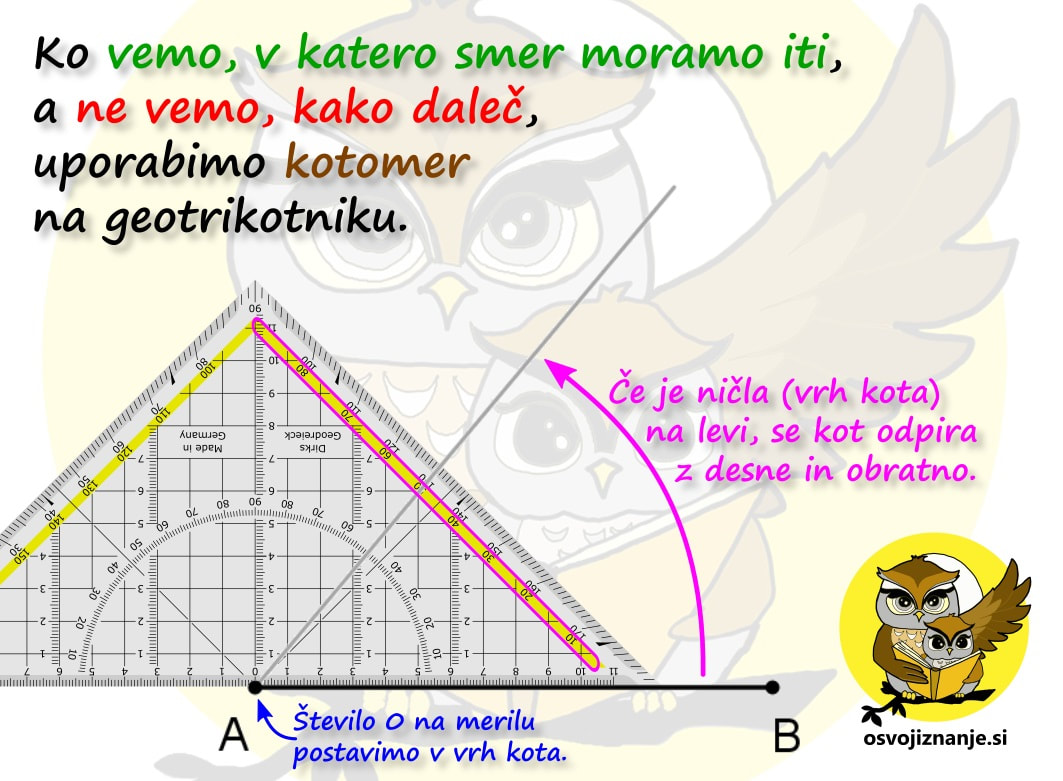
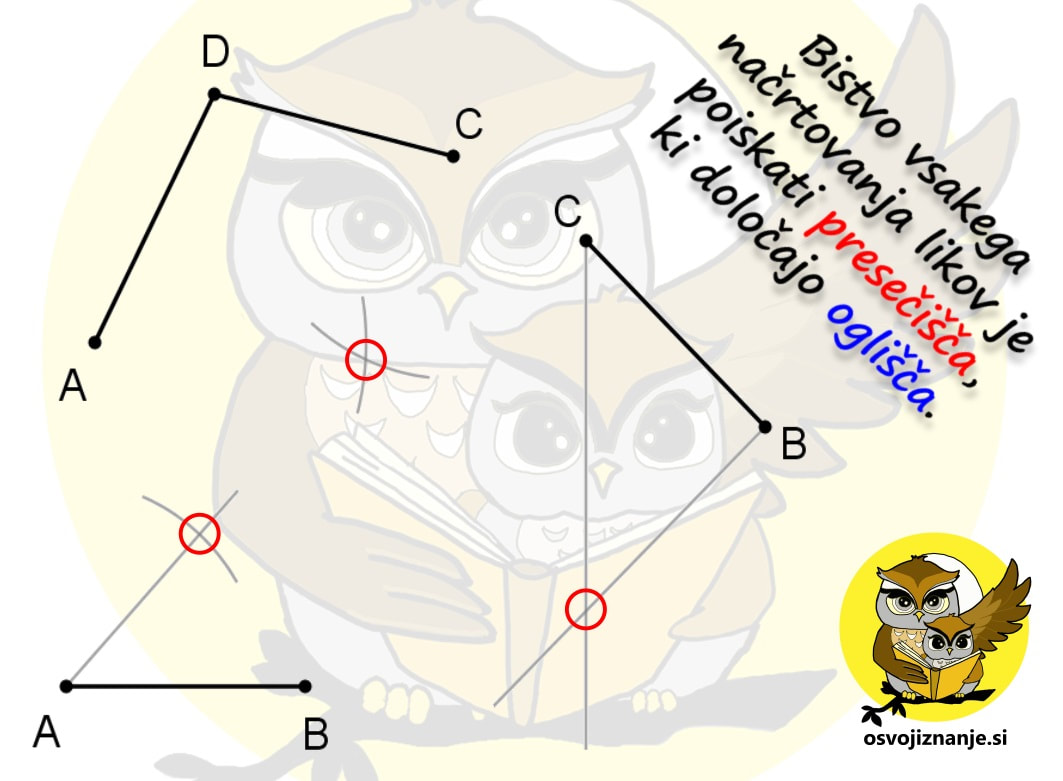
Imate tudi vi v zvezku na desetine navodil za načrtovanje geometrijskih likov »v stilu kuharskega recepta«? Potem pa končno izbrskate tako, ki »diši na podano nalogo«, začnete načrtovati in nekje na sredi ugotovite, da vendarle ni povsem »kompatibilno« z njo? Za take situacije sem pripravil neke vrste univerzalno navodilo, kjer najdete odgovor (skoraj) na vsako vprašanje v zvezi z načrtovanjem, ne glede na to za kakšen geometrijski lik gre. Mora biti na skici lik vedno enako označen? Ni važno, na kakšen način označimo sestavne dele, pomembno je le to, da se skice med načrtovanjem držimo. Kako na skici označiti poznane vrednosti (podatke)? Lahko jih obkrožimo, še bolje pa je na primer pobarvati kar celo stranico ali kote s kraki vred; te lahko tudi podaljšamo, da si bomo lažje ustvarili »miselni tok«. Kaj je to miselni tok? Z njim opišemo strategijo načrtovanja. Gre za neke vrste »drugo skico«, na kateri niso označeni le podatki, ampak predstavlja kar celoten, prostoročno narisan geometrijski lik. Bistvena sestavina miselnega toka pa so označeni koraki načrtovanja. Njegovo nastajanje si lahko predstavljamo kot neko generalko pred »ta pravim« načrtovanjem s šestilom in ravnilom. Ko načrtovanje enkrat že dovolj obvladamo, miselnega toka ni potrebno več risati, ampak je lahko zgolj »v glavi«. Ali pri načrtovanju lahko obrnem list? Seveda. :) Če si recimo navajen, da trikotnik začneš risati pri vodoravni stranici oziroma »od spodaj navzgor«, je to lahko tudi kakšna od poševnih stranic, le pravilno je potrebno zasukati list oziroma zvezek. Kje začeti z načrtovanjem? Najmanj dela imamo, če začnemo pri stranici. Če začnamo s kotom, je nekoliko več risanja, a imamo zato kasneje manj dela, saj imamo na sliki že več kot polovico trikotnika. Če imamo podano višino, lahko najprej narišemo »cesto« ... Kaj je naloga geotrikotnika? Z njim odmerimo točno določeno dolžino (ravnilo) in velikost kotov (kotomer). Katero merilo na kotomeru moramo gledati? Kot se "odpira" tako, kot se odpirajo vrata s tečaji v vrhu kota. Z odpiranjem kota se povečuje njegova velikost, s tem pa tudi številke na merilu kotomera. Uporabimo lahko tudi preprosto pravilo »kontra strani«: če je vrh na levi, se kot odpira z desne (povečevanje številk z desne) in obratno. Zakaj potrebujem šestilo? Z njim začrtamo, do kam bo segala daljica (stranica lika), katere dolžina je znana, a poznamo položaj je enega od njenih krajišč. V tem primeru »mero vzamemo« z geotrikotnikom, šestilo zapičimo v znano krajišče in začrtamo krožnico v smeri, v katero »sumimo«, da bo stranica potekala. Podobno kot pri iskanju ubežnika iz zapora ali zablodele živali. Kaj je bistvo vsakega načrtovanja geometrijskega lika? Glavna stvar, ki jo iščemo pri načrtovanju, so presečišča. Ko imamo vsa presečišča, ta samo še povežemo z ravnimi črtami in imamo lik. Presečišča dobimo bodisi s sekanjem krožnih lokov in/ali poltrakov. Prve na podlagi podatkov o dolžini daljic zarišemo s šestilom, druge pa na podlagi velikosti kotov z geotrikotnikom. |
ARHIV
May 2024
KATEGORIJE
All
|

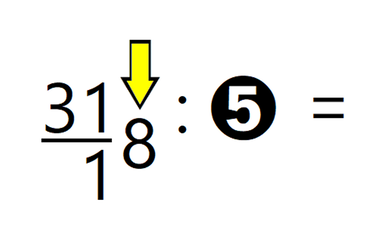
















 RSS Feed
RSS Feed
