V višjih razredih osnovne šole učenci običajno ne dobijo več vprašanj, zato se morajo znajti sami, kar v bistvu sploh ni tako slabo – celo nasprotno. V bistvu gre za enega pomembnejših korakov v samostojnost.

Kdor se zna samostojno učiti, bo v življenju lahko veliko dosegel.

Da bo pot do samostojnosti lažja, sem vam pripravil nekaj nasvetov, kako se zadeve lotiti.

Priprava na učenje

Preberemo snov v učbeniku in si na podlagi le-te izmislimo vprašanja, na katera skušamo že takoj odgovoriti z lastnimi besedami. Snov je takrat še v kratkoročnem spominu – je še »sveža«.

Vprašanja in odgovore je najbolj priporočljivo zapisati na učne kartice. Te so lahko klasične (na papirju), komur pa bolj ustreza digitalna oblika, lahko preizkusi aplikacijo Anki. Vsaka oblika kartic ima svoje prednosti in slabosti - digitalna je hitrejša za kratke besedilne odgovore, papirna pa za zapletenejše odgovore, pri katerih je včasih potrebno tudi kaj narisati - shemo, miselni vzorec in podobno).

Če ne želimo izdelovati kartic, lahko uporabimo tudi kakšen star zvezek, a pazimo, da odgovorov ne zapišemo takoj pod vprašanji, če ne nas lahko hitro zamika, da bi »preplonkali« odgovor. :)

Pri zapisovanju odgovorov lahko preverimo tudi v zvezek, delovni zvezek in svoje zapiske, če bi lahko kakšen odgovor še "oplemenitili".

Kljub temu, da podčrtovanje ne velja za najboljšo učno metodo, si lahko kakšen del besedila označimo, da ga bomo pri preverjanju rezultatov testiranja lažje našli. Seveda le, če je učbenik naš in ga ne nameravamo prodati naprej, pri lastnih zapiskih pa si pri podčrtovanju lahko damo duška. :)

Učenje

Strokovnjaki priporočajo metodo učenja s testiranjem oz. aktivnim priklicem. Pri tem skušamo po najboljših močeh odgovoriti na zapisana vprašanja oziroma po spominu narisati shemo ali miselni vzorec. Bolj ko pri tem »napenjamo možgane«, več znanja se prenese v dolgoročni spomin, kjer ostane za vedno. Zato, četudi nas zamika, ne poglejmo prehitro med odgovore.

Pred prvim testiranjem vedno počakajmo vsaj en dan, da se novo znanje "uleže" oziroma pustimo, da v vmesnem času kakšno informacijo že pozabimo. Ko se bomo naslednji dan skušali spomniti odgovora, bomo "brskali po spominu", pri tem pa se bodo gradile nove nevronske povezave. Te se bodo še dodatno utrdile ponoči, zato si le privoščimo kvaliteten spanec.

Na vprašanja odgovarjajmo čimbolj mešano, k tistim, s katerimi imamo največ težav, pa se vrnimo pogosteje. Najbolje je uporabiti metodo ponavljanja s presledki, ki jo ima aplikacija Anki že vgrajeno. Zadnji dan pred testom pa pojdimo še enkrat čez vsa vprašanja.

Testiramo se lahko sami, lahko nas kdo vpraša, lahko se izmenično sprašujeva s sošolcem, pomaga pa tudi, če odgovor na vprašanje komu razložimo (Protégéjev efekt).
 
Vprašanja in odgovori naj bodo urejeni (razporejeni po predmetih in poglavjih posameznega predmeta) in »varno shranjeni«. Za vprašanja in odgovore v klasični obliki je zelo priročna vložna mapa, v katero lahko dodamo tudi kakšen miselni vzorec, ki povzema določeno snov, za učne kartice na papirju ali kartonu pa kakšna škatlja od čevljev. Kartice, ki spadajo skupaj, lahko spnemo z elastiko.

Dodatno branje:
https://modraskrinjica.wordpress.com/2022/07/21/aktivni-priklic-najboljsi-nacin-ucenja/
https://modraskrinjica.wordpress.com/2023/01/26/nasvet-za-anki-kartice-napisi-s-svojimi-besedami/
https://modraskrinjica.wordpress.com/2023/01/31/anki-moje-najboljse-orodje-za-ucenje/

Učenje je lažje, če je le-to zanimivo. Zanimivega pa si ga naredimo lahko le sami in sicer tako, da smo namesto "buljenja v knjigo" bolj aktivni - si izdelujemo izpiske ter jih urejamo s pomočjo t.i. organizatorjev znanja. Ti naj bodo čim bolj vizualni, da si bomo snov lažje zapomnili.

Obstaja cela kopica organizatorjev znanja, najbolj priljubljeni so grafični. Da se bomo med njimi lažje znašli, sem pripravil slovarček le-teh.

Z organizatorji znanja lahko opremimo tudi zadnje strani učnih kartic (flashcards) pri učenju po metodi aktivnega priklica, o kateri si več lahko preberete tule.

​Viri: ZRSŠ, Wikipedia, Spretnosti učenja, Understood

Znati se učiti je veščina, s pomočjo katere se lahko naučimo praktično vse, kar želimo. Učinkovito in brez pretiranega stresa, znanje pa se nam vtisne globoko v spomin, od koder ga lahko enostavno prikličemo.

Ko se pogovarjamo o učenju učenja, je koristno poznati pojme, ki so opisani v nadaljevanju.

Reference: Inner Drive, Love to teach, Wikipedija, Modra skrinjica, Understood

V bistvu ste lahko veseli, da ste jih dobili, sicer bi jih morali napisati sami. :)

Ja, je kar stres, ko mali nadebudnež prinese domov kopico vprašanj, ampak ta naj bi bila zgolj za vodilo, kaj je potrebno znati. Namesto "predelave" teh vprašanj ima vsak lahko popolnoma svoj način učenja, ampak ga, priznajmo si, le redkokdo uporabi. Sploh sproti. Večina se v dobrem tednu nauči odgovore in "poizkusi srečo" na testu.

Da ne bomo samo kritizirali, imam za vas nekaj idej, kaj "početi" s temi vprašanji.

Fotokopiranje in razrez

• vprašanja fotokopiramo (pomagamo si lahko s telefonom, jaz uporabljam Tiny Scanner),
• jih razrežemo,
• poiščemo odgovore v zvezku (učbeniku, delovnem zvezku ...) in
• nalepimo listke z vprašanji v zvezek, vsakega na mesto, kjer se »skriva« odgovor nanj.

Če so se v šoli že pripravljali na test, imajo pogosto v zvezku odgovore zapisane tik pod vprašanji. V tem primeru lahko fotokopiramo vprašanja in odgovore skupaj in jih razrežemo, nato pa otrok »išče pare«.

Samolepilni listki s številkami vprašanj

• Oštevilčimo vprašanja, če še niso.
• Številke vprašanj zapišemo na samolepilne (post-it) listke.
• Listke prilepimo v zvezek, vsakega na mesto, kjer se »skriva« odgovor nanj.

Če za učenje uporabljamo poleg zvezka tudi učbenik in/ali delovni zvezek, kar je seveda priporočljivo, isto številko vprašanja zapišemo na več listkov in enega prilepimo na primer v zvezek, drugega pa v učbenik, lahko pa tudi na več mest v isti knjigi, če je odgovor bolj razpršen.

Pri tej metodi fotokopiranje ni potrebno, je pa potrebno imeti list z vprašanji vedno na vidnem mestu. Če je ta prilepljen v zvezek, pa – spet kopiramo. :)

Učne kartice (angl. flashcards)

• Vprašanja zapišemo na sprednjo stran učnih kartic.
• Otrok v zvezku (učbeniku, delovnem zvezku ...) poišče odgovore.
• Starši pregledamo odgovore in jih po potrebi skupaj z otrokom dopolnimo.
  
  

Učne kartice otrok lahko nato uporabi tudi za nadaljnje učenje.

Če želimo poleg utrjevanja učne snovi »potrenirati« tudi pisanje, otrok lahko na kartice zapiše tako vprašanja kot odgovore. Starši pa pri tem malo popazimo, da se kakšno vprašanje »ne izgubi«.
 
Poleg omenjenih seveda obstaja še veliko drugih načinov učenja, nekaj jih najdete tudi v preostalih člankih rubrike »Učenje in organizacija«, če pa imate kakšno idejo tudi sami, vabljeni, da jo delite z nami v Facebook skupini.

Če se namesto na pamet učimo z upoštevanjem povezav in medsebojnih odvisnosti, je učenje veliko bolj učinkovito, poznavanje celotne slike (namesto nepovezanega kupa dejstev) pa zahteva tudi manj časa pri ponavljanu naučene snovi, recimo pred testom.

Oglejmo si primer. Če se npr. pripravljamo na test računanja z ulomki, moramo ponoviti vse štiri računske operacije ter tudi vse oblike števil, ki lahko nastopijo v računu: »klasičen« ulomek, celi del in ulomek, manjši od 1, decimalno število, celo število ... potem je tu lahko še kakšen oklepaj, morda koren ali potenca ... Če bi radi pred testom ponovili vse kombinacije, bi nam vzelo kar nekaj časa.

Če pa namesto računanja vseh kombinacij razmislimo raje o tem, kako se določene množice števil »obnašajo« pri posameznih računskih operacijah, kaj imajo določena »srečanja« skupnega, kje so razlike in poiščemo še kakšno povezavo oziroma odnos, nam to vzame veliko manj časa.

Če namesto vseh kombinacij po Paretovem načelu (za mnoge pojave velja, da 20 % vzrokov povzroči 80 % posledic) naredimo le bistvene in pri tem pazimo na čimbolj enakomerno razporeditev nastopajočih parametrov kot so npr. računske operacije (seštevanje, odštevanje, množenje, deljenje ...) in števila (cela, decimalna, ulomki ...), bomo končali bistveno prej, pripravljeni pa ne bomo nič manj, kot če bi šli čez vse kombinacije.

Ko se nekaj učimo, nam močno pomaga, če se lahko opremo na nekaj, kar že poznamo.

V matematiki so to konkretni materiali – pri štetju so nepogrešljivi kamenčki, fižolčki, bombončki ... ;) Nadalje pri seštevanju uporabljamo paličke ali trakove različnih dolžin, ti so uporabni tudi pri primerjanju vrednosti ter odštevanju. Ko spoznamo množenje in deljenje, ena dimenzija ni več dovolj, zato uporabimo na primer polja ploščic. O tem sem se razpisal že v eni izmed predhodnih objav.

Zrelejši ko smo, vedno bolj si znamo predstavljati pojme tudi brez tega, da bi jih »prijeli v roke«. A prehitra abstrakcija vseeno ni dobra. Sploh ne popolna. Zato tudi tisti, ki smo »z matematiko že na ti«, :) radi uberemo neke vrste srednjo pot – z risanjem. O pomembnosti vizualnih predstav sem tudi že pisal.

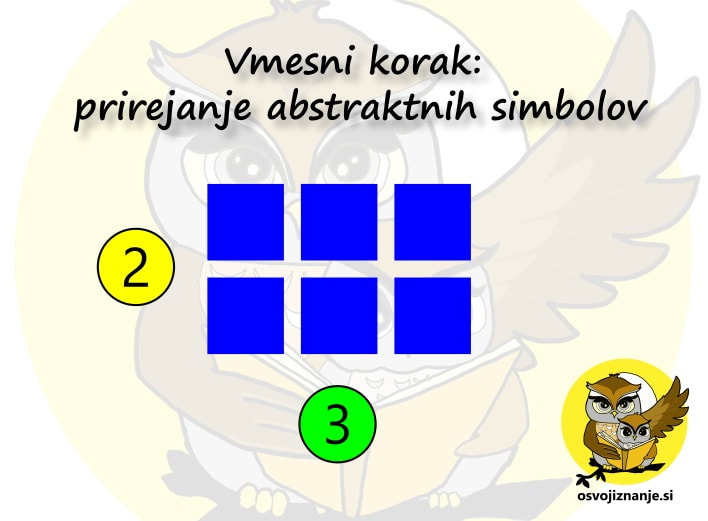
Tako vizualne kot konkretne predstave imajo lahko različne nivoje abstrakcije. Ko si neko vrednost znamo predstavljati tudi brez dejanskega preštevanja, lahko naredimo »korak naprej« in ji priredimo na primer neko barvo in/ali obliko. Jaz sem v moji namizni igri recimo desetice označil z rdečimi kvadratki, enice z modrimi, praštevila pa s krožci različnih barv. Omenjena abstrakcija nam pomaga, da lahko gradimo še kompleksnejše strukture, ki jih z osnovnimi gradniki ne bi mogli, bodisi zaradi pomanjkanja materiala ali prostora na listu, predvsem pa bi se s tem zmanjšala preglednost. Ta pa je ključnega pomena za razumevanje koncepta. In te »vmesne variante« so idealne za predstavljanje (zahtevnejših) konceptov.

Sprva so naši modeli brez številk, ko pa ta nivo abstrakcije presežemo, jih lahko vključimo zraven. Primeri takega modela so številski trak, trikotniki z računskimi operacijami in podobno. Zanimiva je recimo tudi »seštevalno-odštevalna kača«, ki smo jo pred dnevi izdelali z otroki. Zelo podobno lahko naredimo tudi za množenje in deljenje.

Ko nek koncept popolnoma osvojimo, lahko računamo zgolj še s številkami, kar pa še ne pomeni, da na take in drugačne pripomočke lahko pozabimo.

Dejstvo je, da so v resničnem življenju koncepti med seboj prepleteni in vsaka kombinacija le-teh je za nas lahko nov izziv. En tak primer so recimo besedilne (in kasneje še težje problemske) naloge. Za marsikatero si niti predstavljamo ne, kako bi jo lahko rešili drugače kot pa s pomočjo slike.

Je pa koristno didaktične pripomočke poznati tudi takrat, ko pomagamo tistim, ki določene snovi še niso osvojili, bodisi v vlogi nesebične sošolke oziroma sošolca bodisi kot učitelji ali starši.​

… a upa, da nobena izmed njih ne bo prava.

Sliši se nekoliko neobičajno, a najboljši način za predstavljanje nekega abstraktnega pojma je vedno lasten način, tisti, ki si ga »izmislimo« sami. Kar pa še ne pomeni, da tuje ideje niso dobre. So nepogrešljiva osnova, na podlagi katere »izumimo« svojo metodo oziroma jo obogatimo.
 
Velikokrat slišimo, da kakšna ideja »ne drži vode«, pa ne le v šoli, tudi na splošno. Take dileme se največkrat pojavljajo ob nasvetih za vzgojo otrok :) . To je do določene mere res – tuja ideja je le redko popolnoma primerna, po drugi strani pa ima verjetno prav vsaka v sebi nekaj, kar se splača preizkusiti oziroma vsaj delno povzeti ter s tem obogatiti svojo idejo.
 
Zato se ob spoznanju, da neka ideja ni dobra za nas, skušajmo odzvati konstruktivno. Dejstvo, da smo sami ugotovili njeno neustreznost, dokazuje, da razmišljamo na pravi način - aktivno in kritično, sedaj pa moramo le še energijo namesto v kritiziranje vložiti v iskanje delčkov te ideje, ki bi jih lahko uporabili za obogatitev lastnih idej.
 
Vrnimo se k razlagi.

Učenci od učne ure »odnesejo več«, če učitelj oziroma inštruktor, pa tudi starši, ko pomagajo pri domačem delu, namesto »klasične« razlage s pripovedovanjem več sprašuje. Tak način razlage v bistvu najbolj ustreza prav staršem, ki niso obremenjeni z vso teorijo, po drugi strani pa svojega otroka najbolje poznajo. Vprašanja v stilu:

• »Kaj meniš o tem?« in
• »Kako bi se lotil tega?«

poskrbijo, da je otrok pri učenju aktiven in ima večjo motivacijo za to, da bo neko snov dejansko razumel, ne le »na pol preslišal« in se pred testom na pamet naučil pravilne odgovore. Kadar se »klasični« razlagi ne moremo izogniti, pa to skušajmo »odeti v tančico skrivnosti«, da pri učencih vzbudimo radovednost.
 
Če je učencev več, lahko v razredu »viharimo možgane« (angl. brainstorming), nakar učitelj ideje povzame in med njimi naredi nek »most«. Pri razlagi so to lahko neki različni pogledi na obravnavano tematiko, pri reševanju problemskih nalog pa različne strategije reševanja le-teh.
 
Predvsem pri naravoslovnih predmetih, na primer pri matematiki, spodbujajmo tudi čim več risanja in/ali uporabo didaktičnega materiala, saj na tak način najlažje preverimo razumevanje koncepta. Začnimo z enostavnejšimi primeri, nato dodajajmo detajle. Če je pretežko, se vrnimo korak nazaj.
 
»Vračanje nazaj« sicer pomeni dodatno porabo časa, ki ga učiteljem že tako ali tako primanjkuje, ampak je za gradnjo trdnih temeljev znanja nujno potrebno. S stalnim hitenjem naprej si učitelj dela medvedjo uslugo, saj učenci, ki »izgubijo rdečo nit«, lahko hitro postanejo  nezainteresirani, s čimer se njihova »luknja v znanju« le veča, značajsko živahnejši pa pogosto tudi motijo pouk. Tudi mizar mora tu ali tam »nabrusiti žago« :) .
 
Kaj pa storiti, ko se »zalomi«?

Pri reševanju nalog, pa najsi bo v šoli ali pri domači nalogi, se velikokrat zgodi, da rezultat ni pravilen. Kljub temu skušajmo ohraniti pozitivno vzdušje in

• namesto: »To je napačen rezultat,«
• ali celo: »Tvoj način reševanja je napačen,«
  
  

otroka oziroma učenca raje vprašajmo, kako je prišel do takega rezultata. Ponudimo mu možnost, da nam korak za korakom razloži potek reševanja in ga v točkah, kjer podvomimo v pravilnost, ustavimo ter z njim začnemo konstruktivni pogovor na način:

• »Tega pa ne razumem, mi lahko razložiš, čemu si to naredil tako?« ali
• »Zanimivo razmišljanje, bi ga znal upodobiti na sliki?«

Na podlagi narisane skice je običajno veliko lažje sklepati o razumevanju, kot pa zgolj iz besed, saj otroci še nimajo tako razvitega govornega izražanja. Omenjeno metodo lahko uporabimo tudi takrat, ko nismo prepričani, da je učenec nalogo rešil sam.
 
Če prepoznamo (napačno) metodo, ki jo je uporabil, mu situacijo lahko razložimo takole:

• »Postopek, ki si ga izbral, si izpeljal povsem pravilno, a na žalost ni primeren za to nalogo. Zato kljub temu, da se med računanjem nisi zmotil, dobiš drugačen rezultat, kot je v rešitvah. Poskusiva najti še kakšen drug način za reševanje naloge.«

 
Z omenjenimi pristopi ustvarimo visoko motivacijsko okolje za učenje, obenem pa tudi močno zmanjšamo verjetnost za »slabo voljo«, ki je močan demotivator, tako pri pouku kot pri reševanju domače naloge.
 
Starši otroku ob nerazumevanju snovi, ki je bolj življenjske narave, običajno pomagamo glede na lastne izkušnje, ko gre za nek matematični postopek, pa pobrskamo po spominu in mu ga razložimo tako, kot se ga spomnimo še iz naših šolskih dni.

Pa to, kar povemo, res razumemo?
 
Nekaj časa nazaj sem sodeloval v spletni razpravi o tem, zakaj morajo otroci seštevati in odštevati »v vrsti«, ko pa bi to po mnenju nekaterih staršev lahko veliko preprosteje naredili »v stolpcu«. Marsikateri starš se slednjega postopka še dobro spomni iz osnovne šole in ga uporablja tudi sicer v življenju, kadar je potrebno računati »na roke«. Ne zaveda pa se, da računanje »v stolpcu« ni isto kot računanje »v vrsti«, še več, prvo je zgolj postopek, ki se ga naučimo na pamet in izvajamo avtomatizirano, drugo pa omogoča dejansko razumevanje koncepta teh dveh računskih operacij. In koncept je tisto, kar otrok potrebuje, da si bo lahko zgradil trdno osnovo za naprej.
 
Zato je še toliko bolj pomembno, da pogovor z otrokom teče v obe smeri, saj bomo le na ta način ugotovili, ali otrok snov res razume, pa tudi sami bomo morda prišli do kakšnega novega spoznanja, ko bomo na določeno temo pogledali še z drugega, zrelejšega zornega kota. Mogoče se nam zgodi celo kakšen »aha« trenutek :) .

Levi možganski polobli pripisujemo zasluge za logiko, abstraktno mišljenje in prostorske predstave, desni pa za domišljijo, kreativnost in čutnost.

Med učenjem ne gre ne brez ene ne brez druge, saj stalno sodelujeta, lahko bi rekli, da se "medsebojno napajata".

Oglejmo si primer: Če želimo biti kreativni (desna stran), moramo imeti trdno temeljno znanje (leva stran), ki ga najlažje pridobimo ravno s kreativnostjo pri učenju - no, pa smo spet pri desni strani :)

Tiste, ki še vedno mislite, da je poštevanka zgolj niz podatkov, ki si jih je potrebno zapomniti, na pamet, brez razmisleka, moram na žalost razočarati.
 
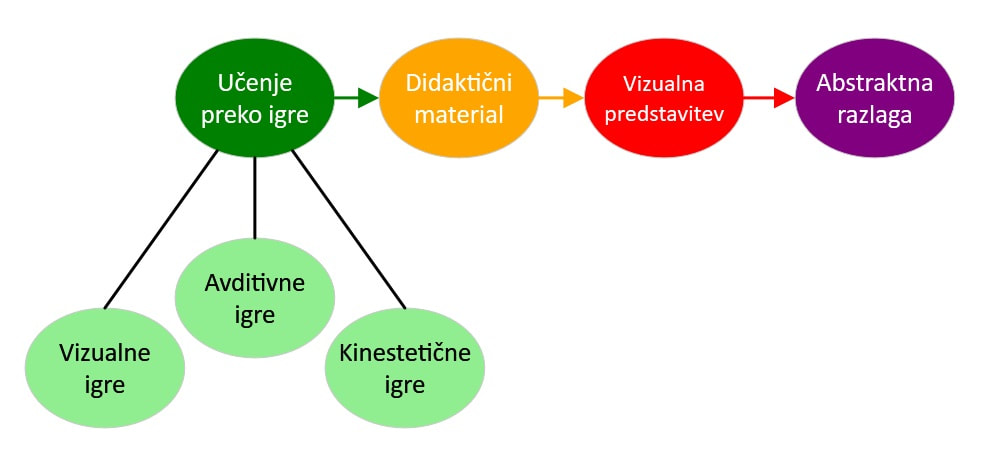
Tako kot matematika ni le predmet »za levo možgansko polovico«, je tudi poštevanka več kot le skupek med seboj zmnoženih števil.
 
Matematika je močno povezana z umetnostjo, ustvarjalnostjo, občutki in čustvi, ki jih povezujemo z desno možgansko poloblo (o tem si več lahko preberete v prispevku o STEAM). Eden pomembnejših občutkov je občutek za lepo, pa naj bo to lepota narave ali umetnostnih del. Tudi matematika je v svojem bistvu »lepa«, čeprav se na žalost še vedno najdejo ljudje, tudi med učiteljskimi vrstami, ki se na vse pretege trudijo, da bi dokazali nasprotno, včasih celo nevede, ko v teste vključujejo naloge, ki nimajo »lepega« rezultata. Res je, matematika ni lahek predmet in pot do rešitve pogosto ni enostavna, ampak nekaj zadovoljstva na koncu si pa zasluži prav vsak. Tako, kot po težavnem vzponu na goro.
 
Mar ne bi vsak otrok rad imel na učenje poštevanke lepe spomine? Barvite, slikovite, povezane z vsemi čutili, tudi za sluh in tip?
 
Če pogledamo globlje, v bistvo poštevanke, opazimo, da so računi, ki jih vsebuje, med seboj močno povezani in skupaj tvorijo logično celoto. Čeprav so računi poštevanke na prvi pogled med seboj dokaj različni, je prav vsak izmed njih sestavljen iz delcev, ki izhajajo iz istega nabora, imenujemo jih praštevila. V poštevanki se pojavljata tudi števili 1 in 0, ki nista praštevili, imata pa v matematiki poseben pomen. Več o tem si lahko preberete v prispevku o številih.)
 
Če te, t.i. »osnovne delce množenja« in povezave med njimi predstavimo na učencu prijazen vizualen, avditiven ali kinestetičen način, mu bo tudi celota veliko bolj jasna. In kar je najpomembnejše, poštevanko bo lahko raziskoval samostojno. Pri samostojnem učenju, ki ga »poganja« radovednost, pa vemo, da se zelo veliko naučimo.
 
Večina otrok v učenju poštevanke »na pamet« ne vidi nekega smisla, zato je zanje to zelo mučno opravilo, ob katerem marsikdo doživlja celo travme, ki jim zagnusijo ne le poštevanke, ampak celotno matematiko. Potem pa je tu še »hitrostno ocenjevanje«, kjer se ne znajdejo najbolje in je njihova usoda zapečatena.
 
Zato je zelo pomembno, da poštevanko učencem predstavimo kot nekaj, kar je v tesni povezavi z vsakdanjim življenjem in jim damo možnost samostojnega raziskovanja s pomočjo didaktičnega materiala, ki je lahko zgolj vizualen, lahko pa mu dodamo tudi avditivne in kinestetične elemente.
 
Didaktični material si z nekaj domišljije in kreativnosti lahko pripravi vsak sam, sicer je pa tu namizna igra »Igriva praštevanka«, ki sem jo razvil zato, da se bodo otroci poštevanko učili preko igre, z raziskovanjem in predvsem bolj z veseljem, znanje le-te pa se bo ohranilo za vedno.

Sam sem čuječnost vedno povezoval bolj z duhovnostjo kot z znanostjo, a vedno bolj ugotavljam, da jo močno potrebujemo tudi pri reševanju problemov.

Po Wikipediji je čuječnost namerno zavedanje in neobsojajoče sprejemanje sedanjega trenutka. Ja, sliši se zelo zapleteno, zato si raje oglejmo konkretni primer ;)

Ko pred seboj vidimo matematični problem, se ga dostikrat lotimo z naglico, še posebej, če imamo za njegovo reševanje odmerjen čas. Zato pogosto uberemo pot, ki ni nujno najkrajša, niti ne najlažja. Če smo zraven še "živčni", se verjetnost za napako le še poveča.

Če pa se znamo za trenutek ustaviti in si problem pozorno ogledati, za trenutek pozabiti na boj za končne točke in oceno ter z osredotočenjem na sedanji trenutek skušamo iz situacije izvleči čim več, smo na poti do rešitve deležni veliko manj stresa, posledično pa je tudi možnost za napako manjša.

Čuječnost nam torej pomaga, da se izkopljemo iz "začaranega kroga" oziroma vanj sploh ne zaidemo.

Na spletu lahko najdemo obilico načinov za urjenje čuječnosti (kar malo povprašajte strica Googla :) ), s "treningom" pa lahko začnemo že zelo zgodaj, recimo z opazovanjem rastlin v gozdu ali prometnih znakov ob cesti.

Za konec si oglejmo še en matematičen primer. 

Recimo, da moramo izračunati izraz

72 + 33 + 28 = ?

Kako bi se ga lotili? V vrstici? V stolpcu? Bi najprej sešteli desetice in nato enice?

Pozoren pogled na račun razkrije, da vsota enic dveh izmed števil tvori točno desetico. To sta števili 72 in 28. Če ti dve števili pogledamo še nekoliko pobliže, ugotovimo, da je njuna vsota točno 100.

Pot do rešitve torej lahko zelo preprosta: 72+28=100, temu prištejemo še 33 in dobimo končni rezultat: 133.