Strokovnjaki pravijo, da se naučimo največ, če uporabljamo kombinacijo aktivnega priklica in učenja s presledki (metodi najdete tudi v našem slovarčku).

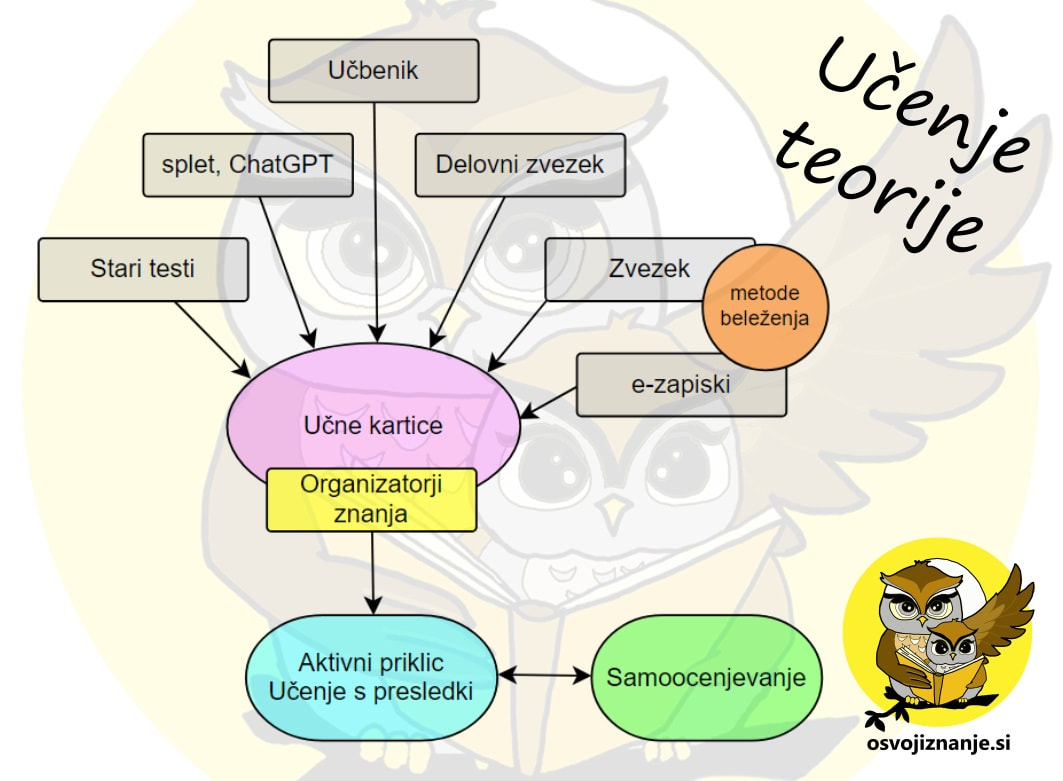
Najbolj elegantno se učenja lotimo z uporabo učnih kartic. Tistim, ki ste uspeli omejiti uporabo zaslonov za zabavo in se ne bojite tehnologije, ;) priporočam Anki, ostali pa seveda lahko naredite »klasične« kartonske kartice, ki imajo na eni strani vprašanje, na drugi pa odgovor. Pomanjkljivost slednjih je le v tem, da moramo med učenjem sami skrbeti za pravi vrstni red in količino ponavljanja v presledkih, medtem ko ima Anki t.i. Leitnerjevo metodo že implementirano. In deluje zelo učinkovito, povem iz prakse.

»Material« za učne kartice lahko črpamo iz različnih virov: zvezek, učbenik, delovni zvezek, stari testi, splet ... Bolj ko je vir urejen, lažja je priprava kartic. Tudi za beleženje obstaja kar nekaj metod, nekaj najbolj zanimivih si lahko ogledate v našem slovarčku.

Priprava kartic zahteva veliko zbranosti, saj moramo vanje vključiti čim več pomembnih dejstev in čim manj »balasta«. Z optimalnimi vprašanji in odgovori lahko močno zmanjšamo čas učenja in se naučimo veliko več kot z »običajnimi« metodami učenja (zopet govorim iz prakse – ko smo pri nas začeli uporabljati Anki, so otroci z manj učenja začeli dobivati boljše ocene).

In kakšna so »optimalna« vprašanja? Ta naj vsebujejo splošno vprašanje, ki mu sledi nekaj konkretnih podvprašanj. Slednja ne morejo zajemati celotne snovi, saj bi jih bilo preveč, so pa odličen opomnik za to, kaj vse je potrebno znati oziroma česa ne smemo »zgrešiti«, ko odgovarjamo na splošno vprašanje. Predvsem, če se učimo sami. Če se učimo v skupini, pa lahko nekoga prosimo, da nam namesto splošnega vprašanja zastavi nekaj konkretnih vprašanj, da vidimo, ali snov ne le znamo, ampak tudi razumemo.

Na zadnjo stran učnih kartic je najbolje vključiti nek grafični organizator, ki zajema vse ključne pojme. Ta nam pomaga, da pri samostojnem učenju česa ne zgrešimo, če nas kdo »vpraša«, pa lahko v miselnem vzorcu, primerjalni tabeli, Vennovem diagramu ali čem podobnem (najzanimivejše najdete v našem slovarčku) najde idejo za konkretno vprašanje.

Odgovor se skriva nekje vmes. Nobena skrajnost ni dobra, zato je najboljša pot vedno tista, ki zajame kar največ pozitivnih lastnosti obeh opcij ter se spretno izogiba pastem.

Marsikdo se boji, da bomo z uporabo umetne inteligence prenehali misliti in vse prepustili »robotom«, s čimer bomo iz dneva v dan postajali bolj, oprostite izrazu, neumni. V skrajnem primeru se to seveda lahko zgodi, ampak ne zaradi umetne inteligence. Še vedno smo mi tisti, ki odločamo in če se odločimo, da tega ne bomo dopustili, smo »na varni strani«.

Kdor je po naravi vedoželjen, ima od umetne inteligence lahko veliko koristi, saj jo lahko uporabi zato, da svoje znanje še bolj oplemeniti. In če jo na tak način uporabljajo tudi učenci, dijaki in študentje, se nimamo ničesar bati.

Zakaj bi se trudili z iskanjem virov za projektno nalogo, če nam pri tem lahko pomaga »pametni asistent«? Mi se raje posvetimo končnemu izdelku, predvsem pa predstavitvi. V mnogo primerih za slednjo, ki je v bistvu najpomembnejša pri vsem tem, zmanjka časa. Predstavitvi moramo nameniti posebno pozornost tudi zato, ker je to edina sestavina naloge, pri kateri nimamo pomoči. To je tisti »pokaži, kaj znaš oziroma zmoreš«, ki bi moral imeti glavno vlogo tudi pri oceni.
S pomočjo umetne inteligence tako lahko prihranimo čas, ki bi ga sicer porabili za rutinska opravila in se namesto tega raje posvetimo efektivnemu učenju, preostanek dneva pa namenimo bolj prijetnim aktivnostim.

Razvoj tehnologije gre naprej, ta pa se odraža na vseh področjih, tudi v šolstvu. Zato upiranje nima smisla, potrebno se je kar najbolje prilagoditi in se »prepustiti toku« s pravo mero zmernosti.

V višjih razredih osnovne šole učenci običajno ne dobijo več vprašanj, zato se morajo znajti sami, kar v bistvu sploh ni tako slabo – celo nasprotno. V bistvu gre za enega pomembnejših korakov v samostojnost.

Kdor se zna samostojno učiti, bo v življenju lahko veliko dosegel.

Da bo pot do samostojnosti lažja, sem vam pripravil nekaj nasvetov, kako se zadeve lotiti.

Priprava na učenje

Preberemo snov v učbeniku in si na podlagi le-te izmislimo vprašanja, na katera skušamo že takoj odgovoriti z lastnimi besedami. Snov je takrat še v kratkoročnem spominu – je še »sveža«.

Vprašanja in odgovore je najbolj priporočljivo zapisati na učne kartice. Te so lahko klasične (na papirju), komur pa bolj ustreza digitalna oblika, lahko preizkusi aplikacijo Anki. Vsaka oblika kartic ima svoje prednosti in slabosti - digitalna je hitrejša za kratke besedilne odgovore, papirna pa za zapletenejše odgovore, pri katerih je včasih potrebno tudi kaj narisati - shemo, miselni vzorec in podobno).

Če ne želimo izdelovati kartic, lahko uporabimo tudi kakšen star zvezek, a pazimo, da odgovorov ne zapišemo takoj pod vprašanji, če ne nas lahko hitro zamika, da bi »preplonkali« odgovor. :)

Pri zapisovanju odgovorov lahko preverimo tudi v zvezek, delovni zvezek in svoje zapiske, če bi lahko kakšen odgovor še "oplemenitili".

Kljub temu, da podčrtovanje ne velja za najboljšo učno metodo, si lahko kakšen del besedila označimo, da ga bomo pri preverjanju rezultatov testiranja lažje našli. Seveda le, če je učbenik naš in ga ne nameravamo prodati naprej, pri lastnih zapiskih pa si pri podčrtovanju lahko damo duška. :)

Učenje

Strokovnjaki priporočajo metodo učenja s testiranjem oz. aktivnim priklicem. Pri tem skušamo po najboljših močeh odgovoriti na zapisana vprašanja oziroma po spominu narisati shemo ali miselni vzorec. Bolj ko pri tem »napenjamo možgane«, več znanja se prenese v dolgoročni spomin, kjer ostane za vedno. Zato, četudi nas zamika, ne poglejmo prehitro med odgovore.

Pred prvim testiranjem vedno počakajmo vsaj en dan, da se novo znanje "uleže" oziroma pustimo, da v vmesnem času kakšno informacijo že pozabimo. Ko se bomo naslednji dan skušali spomniti odgovora, bomo "brskali po spominu", pri tem pa se bodo gradile nove nevronske povezave. Te se bodo še dodatno utrdile ponoči, zato si le privoščimo kvaliteten spanec.

Na vprašanja odgovarjajmo čimbolj mešano, k tistim, s katerimi imamo največ težav, pa se vrnimo pogosteje. Najbolje je uporabiti metodo ponavljanja s presledki, ki jo ima aplikacija Anki že vgrajeno. Zadnji dan pred testom pa pojdimo še enkrat čez vsa vprašanja.

Testiramo se lahko sami, lahko nas kdo vpraša, lahko se izmenično sprašujeva s sošolcem, pomaga pa tudi, če odgovor na vprašanje komu razložimo (Protégéjev efekt).
 
Vprašanja in odgovori naj bodo urejeni (razporejeni po predmetih in poglavjih posameznega predmeta) in »varno shranjeni«. Za vprašanja in odgovore v klasični obliki je zelo priročna vložna mapa, v katero lahko dodamo tudi kakšen miselni vzorec, ki povzema določeno snov, za učne kartice na papirju ali kartonu pa kakšna škatlja od čevljev. Kartice, ki spadajo skupaj, lahko spnemo z elastiko.

Dodatno branje:
https://modraskrinjica.wordpress.com/2022/07/21/aktivni-priklic-najboljsi-nacin-ucenja/
https://modraskrinjica.wordpress.com/2023/01/26/nasvet-za-anki-kartice-napisi-s-svojimi-besedami/
https://modraskrinjica.wordpress.com/2023/01/31/anki-moje-najboljse-orodje-za-ucenje/

Učenje je lažje, če je le-to zanimivo. Zanimivega pa si ga naredimo lahko le sami in sicer tako, da smo namesto "buljenja v knjigo" bolj aktivni - si izdelujemo izpiske ter jih urejamo s pomočjo t.i. organizatorjev znanja. Ti naj bodo čim bolj vizualni, da si bomo snov lažje zapomnili.

Obstaja cela kopica organizatorjev znanja, najbolj priljubljeni so grafični. Da se bomo med njimi lažje znašli, sem pripravil slovarček le-teh.

Z organizatorji znanja lahko opremimo tudi zadnje strani učnih kartic (flashcards) pri učenju po metodi aktivnega priklica, o kateri si več lahko preberete tule.

​Viri: ZRSŠ, Wikipedia, Spretnosti učenja, Understood

Znati se učiti je veščina, s pomočjo katere se lahko naučimo praktično vse, kar želimo. Učinkovito in brez pretiranega stresa, znanje pa se nam vtisne globoko v spomin, od koder ga lahko enostavno prikličemo.

Ko se pogovarjamo o učenju učenja, je koristno poznati pojme, ki so opisani v nadaljevanju.

Reference: Inner Drive, Love to teach, Wikipedija, Modra skrinjica, Understood

V bistvu ste lahko veseli, da ste jih dobili, sicer bi jih morali napisati sami. :)

Ja, je kar stres, ko mali nadebudnež prinese domov kopico vprašanj, ampak ta naj bi bila zgolj za vodilo, kaj je potrebno znati. Namesto "predelave" teh vprašanj ima vsak lahko popolnoma svoj način učenja, ampak ga, priznajmo si, le redkokdo uporabi. Sploh sproti. Večina se v dobrem tednu nauči odgovore in "poizkusi srečo" na testu.

Da ne bomo samo kritizirali, imam za vas nekaj idej, kaj "početi" s temi vprašanji.

Fotokopiranje in razrez

• vprašanja fotokopiramo (pomagamo si lahko s telefonom, jaz uporabljam Tiny Scanner),
• jih razrežemo,
• poiščemo odgovore v zvezku (učbeniku, delovnem zvezku ...) in
• nalepimo listke z vprašanji v zvezek, vsakega na mesto, kjer se »skriva« odgovor nanj.

Če so se v šoli že pripravljali na test, imajo pogosto v zvezku odgovore zapisane tik pod vprašanji. V tem primeru lahko fotokopiramo vprašanja in odgovore skupaj in jih razrežemo, nato pa otrok »išče pare«.

Samolepilni listki s številkami vprašanj

• Oštevilčimo vprašanja, če še niso.
• Številke vprašanj zapišemo na samolepilne (post-it) listke.
• Listke prilepimo v zvezek, vsakega na mesto, kjer se »skriva« odgovor nanj.

Če za učenje uporabljamo poleg zvezka tudi učbenik in/ali delovni zvezek, kar je seveda priporočljivo, isto številko vprašanja zapišemo na več listkov in enega prilepimo na primer v zvezek, drugega pa v učbenik, lahko pa tudi na več mest v isti knjigi, če je odgovor bolj razpršen.

Pri tej metodi fotokopiranje ni potrebno, je pa potrebno imeti list z vprašanji vedno na vidnem mestu. Če je ta prilepljen v zvezek, pa – spet kopiramo. :)

Učne kartice (angl. flashcards)

• Vprašanja zapišemo na sprednjo stran učnih kartic.
• Otrok v zvezku (učbeniku, delovnem zvezku ...) poišče odgovore.
• Starši pregledamo odgovore in jih po potrebi skupaj z otrokom dopolnimo.
  
  

Učne kartice otrok lahko nato uporabi tudi za nadaljnje učenje.

Če želimo poleg utrjevanja učne snovi »potrenirati« tudi pisanje, otrok lahko na kartice zapiše tako vprašanja kot odgovore. Starši pa pri tem malo popazimo, da se kakšno vprašanje »ne izgubi«.
 
Poleg omenjenih seveda obstaja še veliko drugih načinov učenja, nekaj jih najdete tudi v preostalih člankih rubrike »Učenje in organizacija«, če pa imate kakšno idejo tudi sami, vabljeni, da jo delite z nami v Facebook skupini.

Če se namesto na pamet učimo z upoštevanjem povezav in medsebojnih odvisnosti, je učenje veliko bolj učinkovito, poznavanje celotne slike (namesto nepovezanega kupa dejstev) pa zahteva tudi manj časa pri ponavljanu naučene snovi, recimo pred testom.

Oglejmo si primer. Če se npr. pripravljamo na test računanja z ulomki, moramo ponoviti vse štiri računske operacije ter tudi vse oblike števil, ki lahko nastopijo v računu: »klasičen« ulomek, celi del in ulomek, manjši od 1, decimalno število, celo število ... potem je tu lahko še kakšen oklepaj, morda koren ali potenca ... Če bi radi pred testom ponovili vse kombinacije, bi nam vzelo kar nekaj časa.

Če pa namesto računanja vseh kombinacij razmislimo raje o tem, kako se določene množice števil »obnašajo« pri posameznih računskih operacijah, kaj imajo določena »srečanja« skupnega, kje so razlike in poiščemo še kakšno povezavo oziroma odnos, nam to vzame veliko manj časa.

Če namesto vseh kombinacij po Paretovem načelu (za mnoge pojave velja, da 20 % vzrokov povzroči 80 % posledic) naredimo le bistvene in pri tem pazimo na čimbolj enakomerno razporeditev nastopajočih parametrov kot so npr. računske operacije (seštevanje, odštevanje, množenje, deljenje ...) in števila (cela, decimalna, ulomki ...), bomo končali bistveno prej, pripravljeni pa ne bomo nič manj, kot če bi šli čez vse kombinacije.

Levi možganski polobli pripisujemo zasluge za logiko, abstraktno mišljenje in prostorske predstave, desni pa za domišljijo, kreativnost in čutnost.

Med učenjem ne gre ne brez ene ne brez druge, saj stalno sodelujeta, lahko bi rekli, da se "medsebojno napajata".

Oglejmo si primer: Če želimo biti kreativni (desna stran), moramo imeti trdno temeljno znanje (leva stran), ki ga najlažje pridobimo ravno s kreativnostjo pri učenju - no, pa smo spet pri desni strani :)

Tiste, ki še vedno mislite, da je poštevanka zgolj niz podatkov, ki si jih je potrebno zapomniti, na pamet, brez razmisleka, moram na žalost razočarati.
 
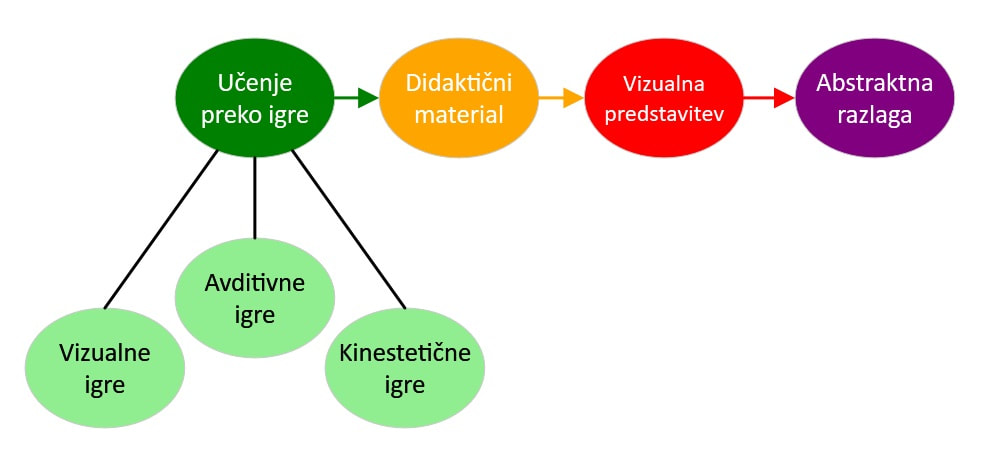
Tako kot matematika ni le predmet »za levo možgansko polovico«, je tudi poštevanka več kot le skupek med seboj zmnoženih števil.
 
Matematika je močno povezana z umetnostjo, ustvarjalnostjo, občutki in čustvi, ki jih povezujemo z desno možgansko poloblo (o tem si več lahko preberete v prispevku o STEAM). Eden pomembnejših občutkov je občutek za lepo, pa naj bo to lepota narave ali umetnostnih del. Tudi matematika je v svojem bistvu »lepa«, čeprav se na žalost še vedno najdejo ljudje, tudi med učiteljskimi vrstami, ki se na vse pretege trudijo, da bi dokazali nasprotno, včasih celo nevede, ko v teste vključujejo naloge, ki nimajo »lepega« rezultata. Res je, matematika ni lahek predmet in pot do rešitve pogosto ni enostavna, ampak nekaj zadovoljstva na koncu si pa zasluži prav vsak. Tako, kot po težavnem vzponu na goro.
 
Mar ne bi vsak otrok rad imel na učenje poštevanke lepe spomine? Barvite, slikovite, povezane z vsemi čutili, tudi za sluh in tip?
 
Če pogledamo globlje, v bistvo poštevanke, opazimo, da so računi, ki jih vsebuje, med seboj močno povezani in skupaj tvorijo logično celoto. Čeprav so računi poštevanke na prvi pogled med seboj dokaj različni, je prav vsak izmed njih sestavljen iz delcev, ki izhajajo iz istega nabora, imenujemo jih praštevila. V poštevanki se pojavljata tudi števili 1 in 0, ki nista praštevili, imata pa v matematiki poseben pomen. Več o tem si lahko preberete v prispevku o številih.)
 
Če te, t.i. »osnovne delce množenja« in povezave med njimi predstavimo na učencu prijazen vizualen, avditiven ali kinestetičen način, mu bo tudi celota veliko bolj jasna. In kar je najpomembnejše, poštevanko bo lahko raziskoval samostojno. Pri samostojnem učenju, ki ga »poganja« radovednost, pa vemo, da se zelo veliko naučimo.
 
Večina otrok v učenju poštevanke »na pamet« ne vidi nekega smisla, zato je zanje to zelo mučno opravilo, ob katerem marsikdo doživlja celo travme, ki jim zagnusijo ne le poštevanke, ampak celotno matematiko. Potem pa je tu še »hitrostno ocenjevanje«, kjer se ne znajdejo najbolje in je njihova usoda zapečatena.
 
Zato je zelo pomembno, da poštevanko učencem predstavimo kot nekaj, kar je v tesni povezavi z vsakdanjim življenjem in jim damo možnost samostojnega raziskovanja s pomočjo didaktičnega materiala, ki je lahko zgolj vizualen, lahko pa mu dodamo tudi avditivne in kinestetične elemente.
 
Didaktični material si z nekaj domišljije in kreativnosti lahko pripravi vsak sam, sicer je pa tu namizna igra »Igriva praštevanka«, ki sem jo razvil zato, da se bodo otroci poštevanko učili preko igre, z raziskovanjem in predvsem bolj z veseljem, znanje le-te pa se bo ohranilo za vedno.

Velikokrat si rečemo: "Ah, saj bo," in gremo na naslednjo snov. Predvsem, če po kakšni aritmetiki sledi geometrija, ko obravnavamo nekoliko drugačne zadeve. In potem pride zopet aritmetika, nekoliko smo že pozabili, nekaj snovi praktično nikoli nismo dobro znali ... in imamo problem.

Kaj storiti, ko se pojavi takšna "luknja" v znanju? Vsekakor se je potrebno ustaviti, saj težave ne bodo minile same od sebe. Stopiti je potrebno nekaj korakov nazaj, do področja, kjer nam je bilo vse še kristalno jasno.

Marsikdo se skuša kljub nepoznavanju koncepta naučiti tekoče postopke (mnogim to celo uspe, predvsem če so šolski testi predvidljivi in vsebujejo vedno enake tipe nalog), a na dolgi rok to ne prinaša koristi.

Ko se sprijaznimo s tem, da bo potrebno narediti nekaj korakov nazaj, se pojavi vprašanje: "Kako pa naj pridobim manjkajoče znanje?" Učitelja, prijatelja, starše oziroma inštruktorja prosimo za ponovno razlago manjkajoče snovi, ob tem pa nam naj ne bo nerodno prositi, da nam poleg razlage z abstraktnimi pojmi (številke, računi) postreže še s kakšno bolj konkretno.

Pomaga že kakšna nazorna slika, najboljši način za to pa je didaktični material, s katerim matematiko ne le vidimo, ampak tudi "začutimo". Veliko didaktičnega materiala lahko najdemo oziroma izdelamo že doma, tako da nam ni potrebno vsega kupovati. Didaktični material se po mojem mnenju v višjih razredih osnovne šole uporablja premalo. Marsikje slišimo, da so otroci za to že "prestari" ... To nikakor ne drži, saj se še stari starši z vnuki radi igrajo z lego kockami :)

Za dojemanje konceptov so zelo primerne tudi didaktične igre. Te so lahko namizne, kinestetični učenci pa se bodo najbolj razveselili iger s čimveč gibanja. Moč je najti tudi igre za tiste, ki se najlažje učite preko zvočnih valov.  Pri marsikateri igri se niti zavedali ne boste, da vsebuje elemente matematike. Te so najboljše :)