|
Ko se boste naslednjič "spopadali" s kakšno od problemskih (ali uporabnih ... hmm ... a neuporabne sploh obstajajo? :) ) nalog, si lahko pomagate z naslednjimi nasveti:
0 Comments
Velikokrat se pri nastavljanju enačbe za problemsko (besedilno, tekstno) nalogo znajdemo pred dilemo, kdaj seštevati in odštevati oziroma kdaj množiti in deliti.
Spodnji primeri so vam pri tem lahko v pomoč:
Besedilo lahko tudi nekoliko obrnemo:
Tole je bolj "ziheraška" metoda, ki sicer lahko vzame nekoliko več časa, je pa zato dokaj pregledna. Razložimo jo na primeru: Pešec prehodi pot 72 metrov. Koliko časa hodi, če je njegova povprečna hitrost 2 m/s? Berimo tekst in si sproti zapisujmo količine, zraven pa njihove podane vrednosti oziroma vprašaj, če te vrednosti iščemo. V oklepaje dodajmo še oznake za te količine, da bomo v nadaljevanju lažje našli ustrezno enačbo.
V šoli se učimo, da morajo biti v izpisu zgoraj podane količine, spodaj (pod črto) pa iskane količine. To sicer lepo zgleda, ni pa nujno za reševanje naloge. Če želite, lahko zgornji seznam še vedno popravite: pot (s) = 72 m hitrost (v) = 2 m/s ---------------------- čas (t) = ? Odsvetujemo pa vam, da za vsako ceno skušate vzdrževati "pravilni" vrstni red podatkov že med samim izpisovanjem le-teh. To vas lahko samo še dodatno zmede. Če vse podane količine navedemo z osnovnimi enotami, se bodo na koncu enote lepo "ujele" in tudi količina, ki jo iščemo, bo v osnovni enoti. Količine, ki niso podane z osnovnimi enotami, pred vstavljanjem v enačbo pretvorimo. Pri tem si lahko pomagamo z desetiškimi potencami. Po pregledu količin, ki nastopajo v zgornjem izpisu, kaj hitro ugotovimo, da nas do rešitve pripelje naslednja enačba: Ker iščemo čas (t), bo enačbo potrebno obrniti. Nekaj navodil za to najdete tukaj. Lahko pa v enačbo preprosto vnesemo vrednosti, na mesto iskane količine pa zapišemo x: Ko x "rešimo" iz enačbe, ugotovimo, da je iskani čas enak 36 sekund.
Marsikdo ne mara vmesnega koraka, imenovanega "izpisovanje podatkov", zato naj vam predstavimo naslednjo metodo, kar na primeru: Kolesar s povprečno hitrostjo 12 m/s prevozi pot 36 metrov. Koliko časa porabi za to pot? Najprej opozorilo. Če želite uporabljati opisano metodo, morate vedno vse količine navesti z osnovnimi enotami! Če so le-te podane z drugimi enotami, jih je potrebno pred vstavljanjem v enačbo pretvoriti. Pri tem si lahko pomagate z desetiškimi potencami. Najprej pobarvajmo tekst. Del, ki se nanaša na posamezno količino, naj bo svoje barve. Količine, ki jih moramo izračunati, podčrtajmo. Te količine se ločijo od ostalih tako, da zraven njih ni navedenega številskega podatka. Kolesar s povprečno hitrostjo 12 m/s prevozi pot 36 metrov. Koliko časa porabi za to pot? Pomislimo, katera enačba bi bila primerna za to nalogo. Glede na obarvan tekst mora vsebovati naslednje količine (v oklepaju so oznake za te količine - tudi te si prikličimo v spomin, da bo enačbo lažje najti):
(Če morda niste med tistimi, ki ne marate izpisovati podatkov, si pa količine v zgornjih alinejah brez sramu zapišite kar na papir, zraven pa seveda še njihove vrednosti. Tak način je tudi nam najbolj všeč, saj je najbolj pregleden) Ko pobrskamo po glavi ali po zvezku, ugotovimo, da gre za naslednjo enačbo: Če nam obračanje enačb ne gre najbolje (komu pa gre :) ), lahko znane količine vstavimo že v njeno osnovno obliko, pa jo bomo potem obračali po mili volji. Neznano količino označimo z x. Da je delo še enostavnejše, lahko vstavljanjem količin enačbo zapišemo s svinčnikom in nato pišemo s krepkejšim pisalom kar čeznjo: Iz enačbe izrazimo x in dobimo iskani čas. Ta znaša 3 sekunde. O tem, kako do njega najlažje pridemo, pa si preberite tule ;)
Sklepni račun Naloge z odstotki lahko zelo elegantno rešimo s pomočjo sklepnega računa. Poznamo dve vrsti nalog z odstotki:
Za naloge tipa "pocenitev" pa lahko uporabimo: Pri izpisu podatkov pazimo na naslednje:
Ker gre za nalogo s pocenitvijo, uporabimo naslednjo drugo predlogo, ki jo ustrezno dopolnimo: V prvo vrstico zapišemo
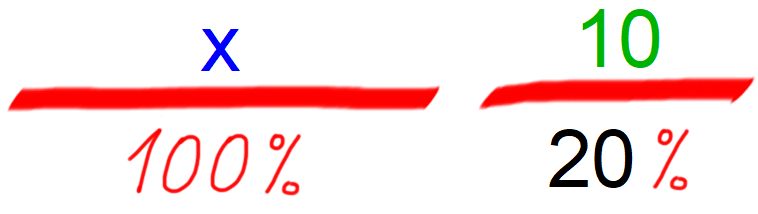
40 €...80% saj je to edini par podatkov, kjer poznamo obe vrednosti (40 € iz besedila naloge, 80% pa posredno, saj jo dobimo z odštevanjem 100%-20%). V drugo vrstico zapišemo par podatkov, kjer eno vrednost poznamo, drugo pa iščemo. Iščemo prvotno ceno hlač (x), zato zapišemo: x...100% Vrednosti križno zmnožimo in izrazimo x. Rešitev: x=50 Odgovor: Prvotna cena hlač je bila 50 €. P.S.: Če bi pa iskali znižanje v €, bi pa v drugo vrstico zapisali y...20% in po križnem množenju izrazili y. Nasvet: S predlogo tipa "pocenitev" lahko rešujemo tudi npr. naloge z raztopinami. Raztopina je v tem primeru "100% osnova", topljenec "znižanje", topilo pa "nova vrednost". Primer: Koliko vode vsebuje 1 liter soka s 60% sadnim deležem? 100% je 1 liter, 60% pa je premosorazmerno 6 decilitrov. 40% je torej preostanek, to je 1 liter - 6 decilitrov = 4 decilitre. Vode je torej 4 decilitre. Več o sklepnem računu najdete tule. Pozor! odstotki spadajo v premo sorazmerje! Računanje z deleži Na marsikateri srednji šoli sklepni račun ni dovolj "fancy", zato je dobro poznati tudi računanje z deleži. Enačba za relativni delež se glasi: r = d/o Nekaj napotkov za "prepoznavanje" posameznih količin v enačbi iz teksta naloge:
Povezava s teorijo o absolutni in relativni napaki Kdor pozna teorijo o absolutni in relativni napaki, si lahko predstavlja naslednje:
Pri primerjavi omenjenih teorij pa je potrebno paziti na naslednjo razliko: Napaka meritve (absolutna ali relativna) je vedno podana kot ±, delež (absolutni ali relativni) pa je odvisen od tega, ali imamo opravka s "podražitvijo" ali "pocenitvijo":
r = d/o Povezava s kemijo - naloge z raztopinami Naloge z raztopinami računamo z enačbo za "pocenitev", pri tem pa je:
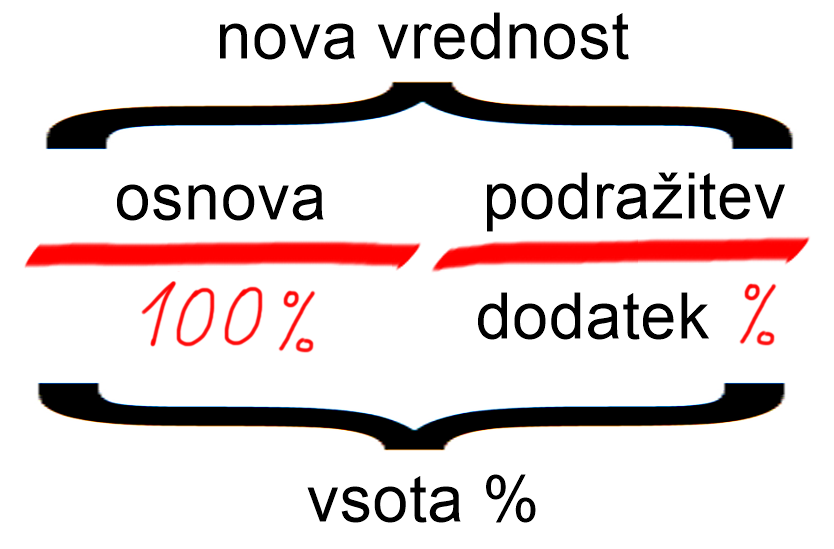
Naloge z odstotki znajo biti kar trd oreh, ko pa jih enkrat "zakapiraš" oziroma "skontaš", pa znajo postati še zabavne ;) Da bodo tudi vam v zabavo, smo vam pripravili ene vrste "kuharski recept za začetnike". Marsikdo bo porekel, da "recept" ne zajema vseh tipov nalog. Res je. Po drugi strani je pa res tudi to, da nihče na začetku ne mara prevelike kompleksnosti. In ravno zaradi njegove enostavnosti je za začetne korake vsekakor uporaben. Za primer vzemimo situacijo, ko nam starši zaradi vestne pomoči pri hišnih opravilih zvišajo žepnino. Za tako situacijo so možni so trije tipi nalog:
Debeli črti na zgornji predlogi nam predstavljata osnovo in dodatek. Nad črtama bomo pisali zneske v €, spodaj pa %. Poleg grafične bomo potrebovali tudi besedno predlogo: Znak % na levi strani besedne predloge se nanaša na % zvišanja žepnine iz našega primera. Splošno ta % pomeni delež dodatka v osnovi. Ne skrbite, če ste se slučajno izgubili. Vse bo bolj jasno v nadaljevanju ;) Besedno predlogo pretvorimo v računsko predlogo:
Vrnimo se k našim trem tipom nalog in jih rešimo, s konkretnimi številkami: 1. Žepnina znaša 50 €. Starši jo povišajo za 10 €. Za koliko % se je žepnina zvišala? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo tako, da na desni strani zapišemo 10/1, križno zmnožimo in izrazimo x. Rešitev: x=20 Odgovor: Žepnina se je zvišala za 20%. 2. Žepnina znaša 50 €. Starši jo povišajo za 20%. Za koliko € se je žepnina zvišala? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo z okrajšanjem ulomka. Rešitev: x=10 Odgovor: Žepnina se je zvišala za 10 €. 3. Žepnino starši povišajo za 20%, kar znaša 10 €. Koliko € je bil znesek žepnine pred povišanjem? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo tako, da na desni strani zapišemo 10/1, križno zmnožimo in izrazimo x.
Rešitev: x=50 Odgovor: Prvoten znesek žepnine je znašal 50 €. Naloge so seveda lahko še težje:
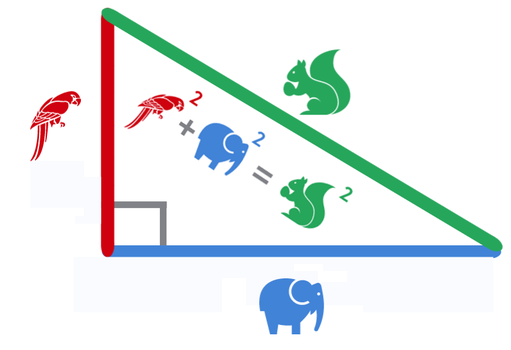
Kadar moramo iz dveh razdalj izračunati tretjo razdaljo, pri čemer sta dve razdalji pravokotni ena na drugo, imamo opravka s Pitagorovim izrekom. Ker smo na testu velikokrat živčni in črke lahko hitro zamenjamo, si ga lahko zapomnimo v obliki simbolov živali :) Poglejmo spodnjo sliko: tretja razdalja (hipotenuza, predstavljena z veverico) je vedno večja od pravokotnih dveh razdalj (kateti, predstavljani s slonom in papagajem): Če iščemo poševno, najdaljšo razdaljo, seštevamo, če pa iščemo kakšno od pravokotnih krajših razdalj, pa odštevamo (seveda manjšo od večje, saj dolžina ne more biti negativna). Ne pozabimo, da so v enačbi kvadrati razdalj, zato moramo vse razdalje kvadrirati in po končanem seštevanju / odštevanju rezultat še koreniti!
Podobno kot pri tem tipu bomo tudi tu seštevali in odštevali, potrebno pa je paziti, da med številkami nastopajo deleži celotne vrednosti (če je le-ta neznana, bo to četrtina od x, 20% od x,...).
"Simpl" varianta vsebuje samo številske vrednosti. Take naloge najlažje rešujemo v obliki tabele: Do rezultata pridemo z enostavnim seštevanjem in odštevanjem.
Problemske naloge tipa...
"Koliko m tega ali onega materiala potrebujemo, če želimo nekaj ograditi, narisati črto okoli nečesa...v izmeri toliko krat toliko oziroma glede na priloženo skico z merami" ...rešujemo s poznavanjem obsega geometrijskih likov. Če ti liki niso pravilni, oziroma preproste enačbe za njihovo ploščino ne obstajajo, jih je potrebno razrezati in potem dolžine posameznih delov sešteti (glej tudi tole). |
Arhiv
December 2023
kategorije
All
|
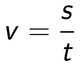
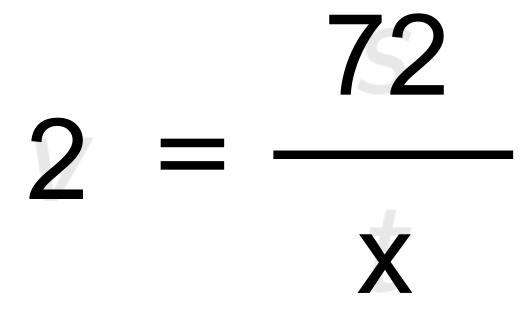
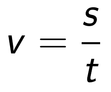
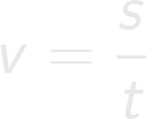
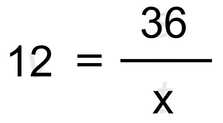




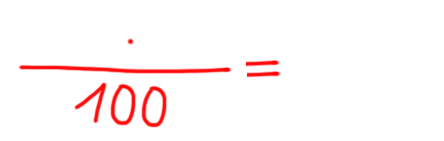


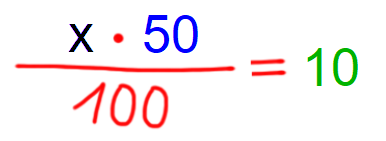


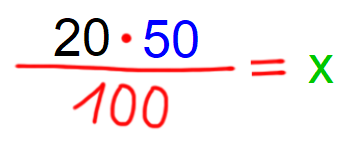
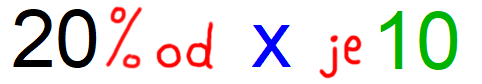
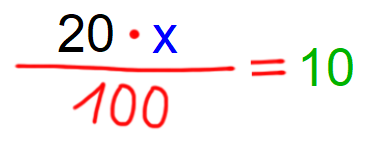


 RSS Feed
RSS Feed
