|
Sklepni račun Naloge z odstotki lahko zelo elegantno rešimo s pomočjo sklepnega računa. Poznamo dve vrsti nalog z odstotki:
Za naloge tipa "pocenitev" pa lahko uporabimo: Pri izpisu podatkov pazimo na naslednje:
Ker gre za nalogo s pocenitvijo, uporabimo naslednjo drugo predlogo, ki jo ustrezno dopolnimo: V prvo vrstico zapišemo
40 €...80% saj je to edini par podatkov, kjer poznamo obe vrednosti (40 € iz besedila naloge, 80% pa posredno, saj jo dobimo z odštevanjem 100%-20%). V drugo vrstico zapišemo par podatkov, kjer eno vrednost poznamo, drugo pa iščemo. Iščemo prvotno ceno hlač (x), zato zapišemo: x...100% Vrednosti križno zmnožimo in izrazimo x. Rešitev: x=50 Odgovor: Prvotna cena hlač je bila 50 €. P.S.: Če bi pa iskali znižanje v €, bi pa v drugo vrstico zapisali y...20% in po križnem množenju izrazili y. Nasvet: S predlogo tipa "pocenitev" lahko rešujemo tudi npr. naloge z raztopinami. Raztopina je v tem primeru "100% osnova", topljenec "znižanje", topilo pa "nova vrednost". Primer: Koliko vode vsebuje 1 liter soka s 60% sadnim deležem? 100% je 1 liter, 60% pa je premosorazmerno 6 decilitrov. 40% je torej preostanek, to je 1 liter - 6 decilitrov = 4 decilitre. Vode je torej 4 decilitre. Več o sklepnem računu najdete tule. Pozor! odstotki spadajo v premo sorazmerje! Računanje z deleži Na marsikateri srednji šoli sklepni račun ni dovolj "fancy", zato je dobro poznati tudi računanje z deleži. Enačba za relativni delež se glasi: r = d/o Nekaj napotkov za "prepoznavanje" posameznih količin v enačbi iz teksta naloge:
Povezava s teorijo o absolutni in relativni napaki Kdor pozna teorijo o absolutni in relativni napaki, si lahko predstavlja naslednje:
Pri primerjavi omenjenih teorij pa je potrebno paziti na naslednjo razliko: Napaka meritve (absolutna ali relativna) je vedno podana kot ±, delež (absolutni ali relativni) pa je odvisen od tega, ali imamo opravka s "podražitvijo" ali "pocenitvijo":
r = d/o Povezava s kemijo - naloge z raztopinami Naloge z raztopinami računamo z enačbo za "pocenitev", pri tem pa je:
0 Comments
Naloge z odstotki znajo biti kar trd oreh, ko pa jih enkrat "zakapiraš" oziroma "skontaš", pa znajo postati še zabavne ;) Da bodo tudi vam v zabavo, smo vam pripravili ene vrste "kuharski recept za začetnike". Marsikdo bo porekel, da "recept" ne zajema vseh tipov nalog. Res je. Po drugi strani je pa res tudi to, da nihče na začetku ne mara prevelike kompleksnosti. In ravno zaradi njegove enostavnosti je za začetne korake vsekakor uporaben. Za primer vzemimo situacijo, ko nam starši zaradi vestne pomoči pri hišnih opravilih zvišajo žepnino. Za tako situacijo so možni so trije tipi nalog:
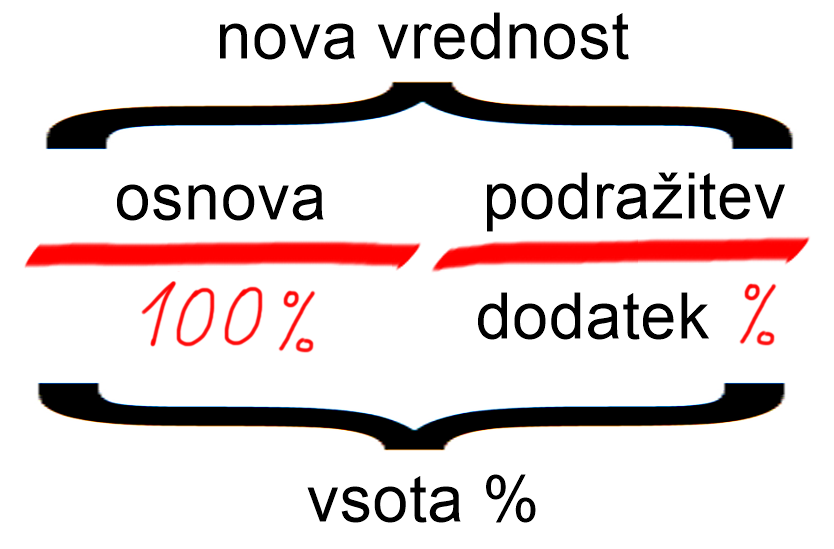
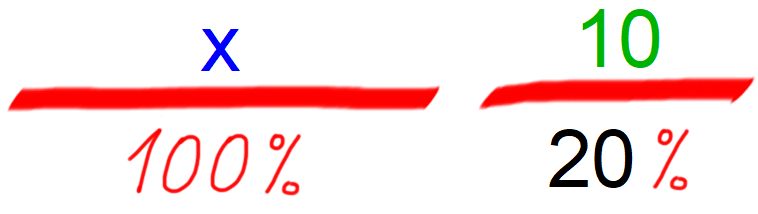
Debeli črti na zgornji predlogi nam predstavljata osnovo in dodatek. Nad črtama bomo pisali zneske v €, spodaj pa %. Poleg grafične bomo potrebovali tudi besedno predlogo: Znak % na levi strani besedne predloge se nanaša na % zvišanja žepnine iz našega primera. Splošno ta % pomeni delež dodatka v osnovi. Ne skrbite, če ste se slučajno izgubili. Vse bo bolj jasno v nadaljevanju ;) Besedno predlogo pretvorimo v računsko predlogo:
Vrnimo se k našim trem tipom nalog in jih rešimo, s konkretnimi številkami: 1. Žepnina znaša 50 €. Starši jo povišajo za 10 €. Za koliko % se je žepnina zvišala? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo tako, da na desni strani zapišemo 10/1, križno zmnožimo in izrazimo x. Rešitev: x=20 Odgovor: Žepnina se je zvišala za 20%. 2. Žepnina znaša 50 €. Starši jo povišajo za 20%. Za koliko € se je žepnina zvišala? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo z okrajšanjem ulomka. Rešitev: x=10 Odgovor: Žepnina se je zvišala za 10 €. 3. Žepnino starši povišajo za 20%, kar znaša 10 €. Koliko € je bil znesek žepnine pred povišanjem? Izpolnimo grafično predlogo. Pri tem pazimo barvno kodo: Problem zapišimo z besedo: Zapišimo račun: Račun rešimo tako, da na desni strani zapišemo 10/1, križno zmnožimo in izrazimo x.
Rešitev: x=50 Odgovor: Prvoten znesek žepnine je znašal 50 €. Naloge so seveda lahko še težje:
|
Arhiv
December 2023
kategorije
All
|




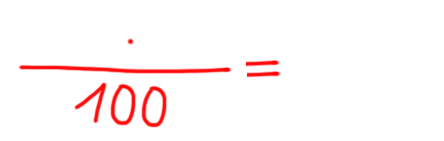


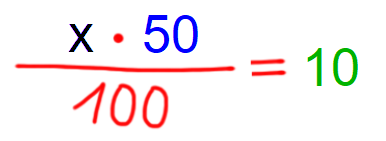


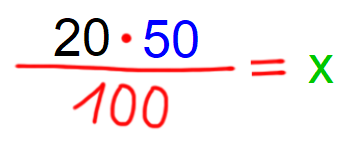
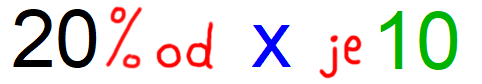
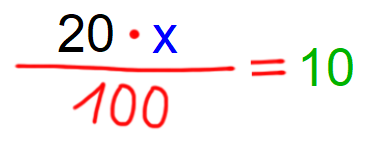

 RSS Feed
RSS Feed
