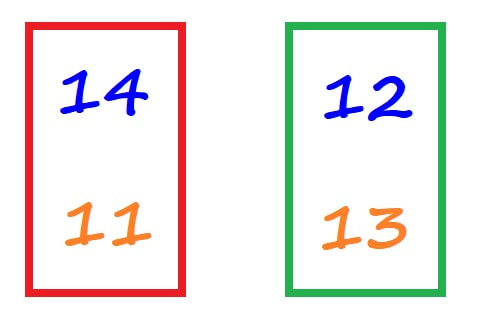
Iz preprostega razloga - ker rezultat potem kar "pade pred nas" :)

​Oglejmo si naslednjo nalogo: 

V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj?

Kdor "obvlada", bo hitro ugotovil, da mora sešteti 14 in 12. Kaj pa tisti, ki se še učijo oziroma imajo težave pri razumevanju?

Pomaga že, če z barvami "opremimo besedilo ...

V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj?

... še lažje pa nam bo, če situacijo skiciramo (poudarek je na "skiciramo", saj smo pri matematiki in ne pri LUM :) )

Sedaj, ko imamo sliko, bomo na vprašanja odgovorili veliko lažje. In to ne le na eno, tudi na kopico le-teh, recimo:

• Koliko deklic je v obeh razredih skupaj? (●)
• Koliko dečkov je v obeh razredih skupaj? (●)
• Koliko učencev je v 2.a razredu? (●)
• Koliko učencev je v 2.b razredu? (●)
• Je v 2.a razredu več učencev ali učenk? Za koliko? (●)
• Je v 2.b razredu več učencev ali učenk? Za koliko? (●)
• V katerem razredu je več deklic? Za koliko? (●)
• V katerem razredu je več otrok (dečki + deklice)? (●●●●)
• ...

V oklepaju so barve, na katere moramo biti pri posameznem vprašanju pozorni.

Led pri reševanju problemskih nalog učenci običajno prebijajo z osnovnimi nalogami "na plus in minus". Starši se ob reševanju domačih nalog velikokrat sprašujemo, kako bi jim pri tem pomagali. Tudi mi imamo za to nekaj predlogov :)

Zadeve gredo običajno "lažje v glavo", če se jih učimo po več skupaj in med njimi iščemo neko relacijo, v našem primeru razliko. Kakšna je razlika med nalogami "na plus" in nalogami "na minus"? Podobna kot razlika med sodelovanjem in tekmovanjem.

Zgornja dva primera lahko služita kot neka referenca, na katero se bodo učenci lahko vedno spomnili, kadar bodo "v škripcih".

Eno izmed osnovnih vodil pri učenju priporoča smer "od znanega k neznanemu", z drugimi besedami osvojitev obravnavanih lastnosti oziroma zakonitosti na dobro poznanem primeru in nato iskanje podobnih vzorcev še v drugih, manj "domačih" situacijah.

"Na minus" pogosto računamo tudi pri nalogah, ko "z danes na jutri" nečesa zmanjka ali pa se nekaj poveča, nas pa zanima razlika, recimo takole:

Velikokrat se pri nastavljanju enačbe za problemsko (besedilno, tekstno) nalogo znajdemo pred dilemo, kdaj seštevati in odštevati oziroma kdaj množiti in deliti.

Spodnji primeri so vam pri tem lahko v pomoč:

• Erazem (b) ima pet jabolk več od  Erika (a): b = a + 5
• Ema (b) ima tri hruške manj od Vala (a): b = a - 3
• Bor (b) ima dvakrat več frnikol od  Nika (a): b = a⋅2 = 2a
• Urška (b) ima štirikrat manj sponk za lase od Zale (a): b = a:4 = a/4

Besedilo lahko tudi nekoliko obrnemo:

• Odvisna spremenljivka y je za šest večja od  neodvisne spremenljivke x:  y = x + 6
• Odvisna spremenljivka y je sedemkrat manjša od neodvisne spremenljivke x: y = x:7 = x/7
• Odvisna spremenljivka y je za tri manjša od petkratne vrednosti neodvisne spremenljivke x:
  y = 5x - 3

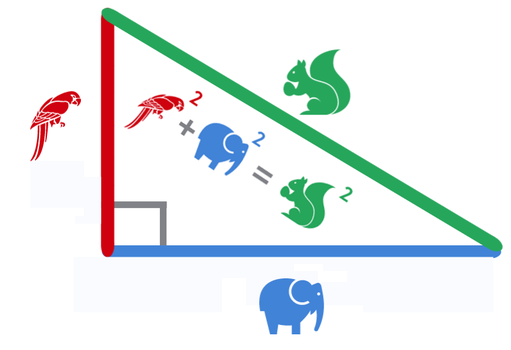
Kadar moramo iz dveh razdalj izračunati tretjo razdaljo, pri čemer sta dve razdalji pravokotni ena na drugo, imamo opravka s Pitagorovim izrekom.

Ker smo na testu velikokrat živčni in črke lahko hitro zamenjamo, si ga lahko zapomnimo v obliki simbolov živali :)

Poglejmo spodnjo sliko: tretja razdalja (hipotenuza, predstavljena z veverico) je vedno večja od pravokotnih dveh razdalj (kateti, predstavljani s slonom in papagajem):

Če iščemo poševno, najdaljšo razdaljo, seštevamo, če pa iščemo kakšno od pravokotnih krajših razdalj, pa odštevamo (seveda manjšo od večje, saj dolžina ne more biti negativna). Ne pozabimo, da so v enačbi kvadrati razdalj, zato moramo vse razdalje kvadrirati in po končanem seštevanju / odštevanju rezultat še koreniti!

Podobno kot pri tem tipu bomo tudi tu seštevali in odštevali, potrebno pa je paziti, da med številkami nastopajo deleži celotne vrednosti (če je le-ta neznana, bo to četrtina od x, 20% od x,...).

"Simpl" varianta vsebuje samo številske vrednosti. Take naloge najlažje rešujemo v obliki tabele:

Problemske naloge tipa...

"Koliko m² tega ali onega materiala potrebujemo, če želimo položiti, tlakovati...stanovanje, dvorišče itd. v izmeri toliko krat toliko oziroma glede na priloženo skico z merami"

...rešujemo s poznavanjem ploščine geometrijskih likov. Če ti liki niso pravilni, oziroma preproste enačbe za njihovo ploščino ne obstajajo, jih je potrebno razrezati in potem ploščine posameznih delov sešteti, kar se prekriva, pa odšteti (glej tudi tole).

Včasih vprašajo tudi, koliko ploščic, tlakovcev...potrebujemo, če so podane mere enega od teh. Takrat moramo izračunati ploščino enega in z njo deliti celotno ploščino.