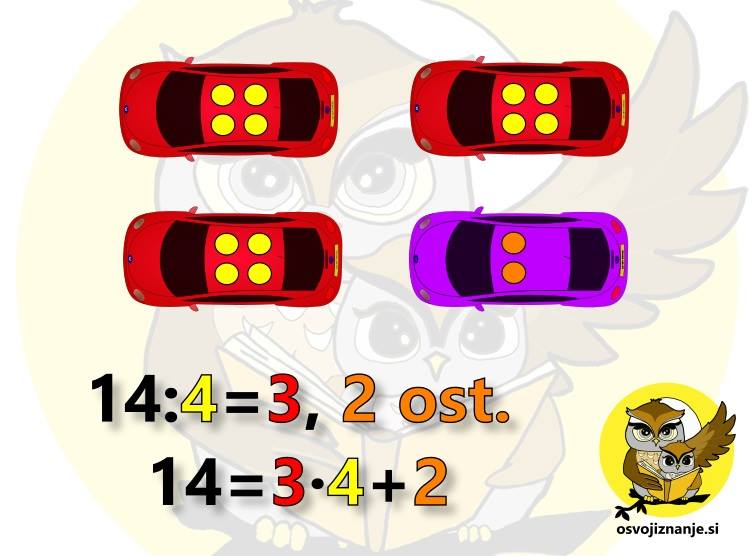
Marsikatero besedilno nalogo lahko rešimo že z enostavnim premislekom. glejmo si dve taki nalogi, pri katerih uporabimo deljenje z ostankom.

Z najmanj koliko avtomobili se lahko pelje 14 oseb, če se v enem avtu lahko peljejo največ štiri osebe?

14 ljudi bomo razdelili v skupine po 4, zato zapišemo račun 14:4. Rezultat deljenja je 3, ostanek pa 2.

Kaj nam pove rezultat? 14 ljudi torej lahko razdelimo v 3 skupine po 4 (3 krat 4 je 12), dva pa "ostaneta zunaj". Za preostala dva človeka moramo torej "naročiti" še en avto, skupaj torej potrebujemo 4. A le trije bodo polni, v zadnjem bosta sedela le dva.

Še dobro, da imamo na voljo dovolj avtomobilov, sicer bi zadnja dva morala iti kar peš ;)

Velikokrat se pri nastavljanju enačbe za problemsko (besedilno, tekstno) nalogo znajdemo pred dilemo, kdaj seštevati in odštevati oziroma kdaj množiti in deliti.

Spodnji primeri so vam pri tem lahko v pomoč:

• Erazem (b) ima pet jabolk več od  Erika (a): b = a + 5
• Ema (b) ima tri hruške manj od Vala (a): b = a - 3
• Bor (b) ima dvakrat več frnikol od  Nika (a): b = a⋅2 = 2a
• Urška (b) ima štirikrat manj sponk za lase od Zale (a): b = a:4 = a/4

Besedilo lahko tudi nekoliko obrnemo:

• Odvisna spremenljivka y je za šest večja od  neodvisne spremenljivke x:  y = x + 6
• Odvisna spremenljivka y je sedemkrat manjša od neodvisne spremenljivke x: y = x:7 = x/7
• Odvisna spremenljivka y je za tri manjša od petkratne vrednosti neodvisne spremenljivke x:
  y = 5x - 3

Problemske naloge tipa...

"Koliko m² tega ali onega materiala potrebujemo, če želimo položiti, tlakovati...stanovanje, dvorišče itd. v izmeri toliko krat toliko oziroma glede na priloženo skico z merami"

...rešujemo s poznavanjem ploščine geometrijskih likov. Če ti liki niso pravilni, oziroma preproste enačbe za njihovo ploščino ne obstajajo, jih je potrebno razrezati in potem ploščine posameznih delov sešteti, kar se prekriva, pa odšteti (glej tudi tole).

Včasih vprašajo tudi, koliko ploščic, tlakovcev...potrebujemo, če so podane mere enega od teh. Takrat moramo izračunati ploščino enega in z njo deliti celotno ploščino.