|
Metod za reševanje besedilnih nalog je celo morje, nekaj jih najdete tudi na blogu, strokovnjaki pa vedno bolj priporočajo t.i. problemski pristop k reševanju, saj so v tem primeru naši možgani najbolj zaposleni in gradijo največ matematičnih povezav.
Tudi pri »igranju s številkami« imamo na voljo več strategij, najbolje pa se obnese tista, ki jo na podlagi predznanja in izkušenj »izumimo« sami. Ob reševanju vsake besedilne naloge v naših možganih namreč zgradimo kar nekaj novih povezav (no, točneje se to dogaja med spanjem, ampak več o tem ob kakšni drugi priložnosti), ki jih kasneje lahko koristno uporabimo. Včasih pomaga, če si besedilno nalogo zgolj poenostavimo, da bi lažje razumeli samo bistvo le-te. Če nismo obremenjeni s »prevelikimi« ali »zakompliciranimi« številkami (na primer takimi s petimi decimalnimi mesti), imamo v delovnem spominu več prostora za razmišljanje o tem, kako bi nalogo rešili. Primer: Ana ima prihranjenih 582,35 EUR, Marko 472,65 EUR, Katja pa 502,33 EUR. Kdo je prihranil največ in kdo najmanj? Kolikšna je razlika med največjim in najmanjšim zneskom? Namesto velikih števil lahko uporabimo manjše, pri čemer upoštevamo razliko njihovih velikosti. Ana ima največ, nato Katja, najmanj ima Marko. Namesto »zakompliciranih« zneskov lahko rečemo, da ima Ana 3 evre, Katja 2, Marko pa 1 EUR. Tu hitro vidimo, da je razlika med Aninim in Markotovim zneskom 2 EUR, račun se glasi 3-1=2. Če sedaj uporabimo »velike« številke, dobimo račun 582,35-472,65. Rezultat pa je naš odgovor. Nalogo si lahko še dodatno poenostavimo z uporabo izrazov »več«, »manj« in »enako« namesto konkretnih števil. Tudi vprašanje za začetek lahko »postavimo na stranski tir«. Tako se res osredotočimo le na razumevanje problema in se ne obremenjujemo z računanjem, vsaj na začetku ne. Kogar zanima še kaj več na to temo, si lahko ogleda naslednji povezavi:
0 Comments
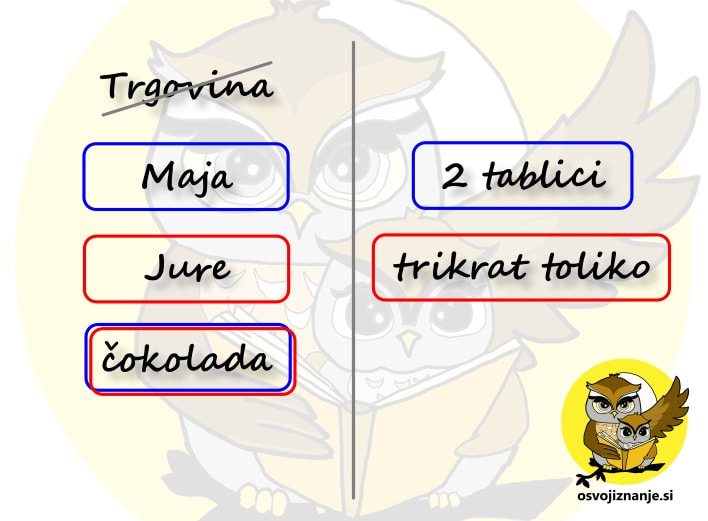
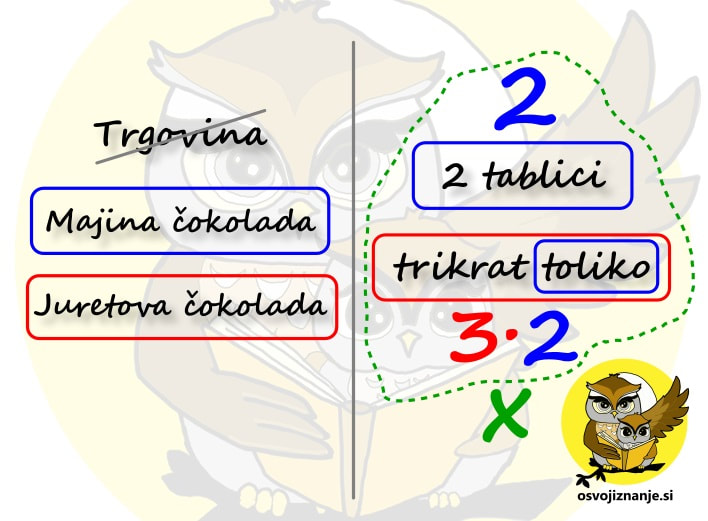
Za vas imam še eno metodo reševanja besedilnih nalog. Mogoče bo pa ravno ta tista, ki se vam bo dopadla. ;) Seveda si jo lahko tudi po želji prilagodite. V bistvu je to celo zaželjeno. Zadeva je popolnoma preprosta. Naj jo razložim na primeru. Besedilna naloga se glasi: »V trgovini je Maja kupila 2 tablici čokolade, Jure pa trikrat toliko. Koliko čokolade sta kupila oba skupaj?« Pa jo rešimo. Najprej:
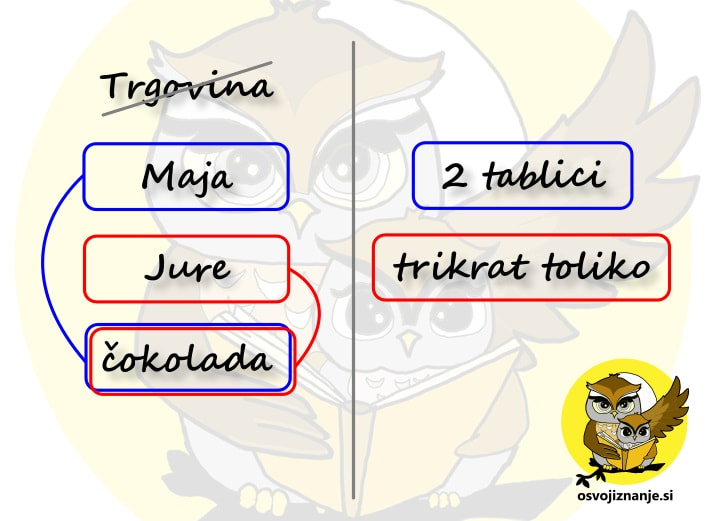
Nato z enako barvo obkrožimo vse, kar spada skupaj. Če kakšna oseba oz. predmet nastopa le enkrat, a pripada več skupinam, jo obkrožimo z več barvami. V našem primeru je to čokolada. Če kakšna oseba oz. predmet ni povezana z nobenim podatkom, jo prečrtamo. V našem primeru je to trgovina. Kako vemo, da oseba oz. predmet ni povezana z nobenim podatkom? Možnosti sta (vsaj) dve:
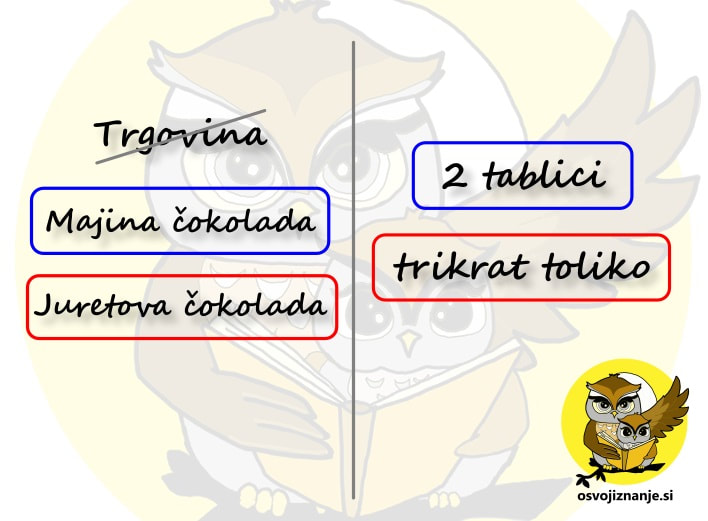
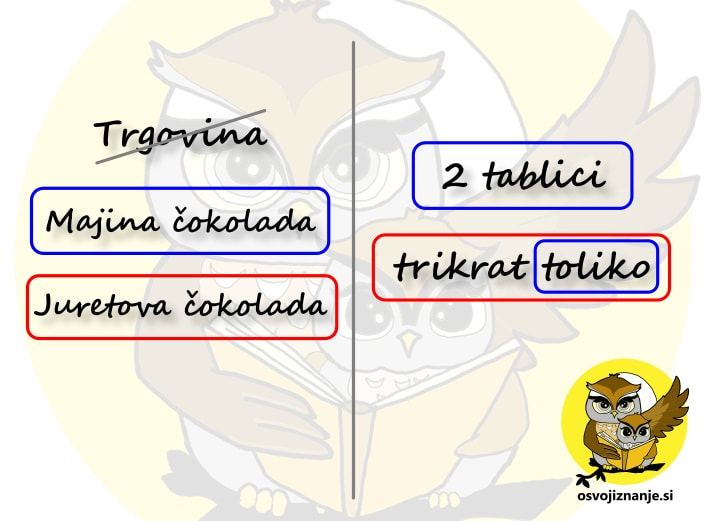
Razmislimo, če z enako barvo obkrožene osebe oz. predmete na levi lahko združimo. Z manj »navlake« bomo lažje nastavili račun. V našem primeru lahko Majo in čokolado združimo v »Majino čokolado«, Jureta in čokolado pa v »Juretovo čokolado«: Sledi zelo pomemben del naloge – poiskati moramo povezavo med podatki. Vsaka besedilna naloga tako povezavo mora vsebovati, sicer je ni možno rešiti. V našem primeru se povezava skriva v besedici »toliko«. Podatek »trikrat toliko« je sicer obarvan rdeče, a besedica »toliko« se nanaša na osebe, predmete in podatke, obarvane modro. Zato besedo »toliko« obkrožimo z modro barvo: Ko imamo vse povezave »pod streho«, si še enkrat oglejmo vprašanje. Kaj moramo izračunati? Ker bomo računali s podatki, se osredotočimo na desno stran lista. V našem primeru nas zanima skupna količina čokolade, torej »moder« in »rdeč« del skupaj. Za še večjo preglednost lahko poleg obkroženih podatkov še na veliko napišemo vrednosti. V našem primeru sta to »modra« in »rdeča« vrednost. Vrednost, ki nas zanima, označimo z vprašajem ali pa kar z neznanko x. Ta naj bo drugačne barve od podatkov. V našem primeru uporabimo zeleno barvo: Če pozorneje pogledamo desno stran lista, vidimo, da nam manjka le še korak do računa. Z zeleno smo obkrožili vrednost, ki nas zanima, torej »moder« in »rdeč« del skupaj. Besedo »skupaj« povezujemo z računsko operacijo »plus«, torej se bo račun glasil:
x=2+3∙2 Oziroma x=8. Maja in Jure sta torej kupila skupaj 8 tablic čokolade. Na koncu pa še napotek. Če je naloga preveč zahtevna zgolj za izpisovanje in obkrožanje podatkov, narišemo skico, kjer nastopajoče predmete in osebe narišemo v obliki čimbolj preprostih simbolov. Oglejmo si naslednji primer: Nika vsak dan preteče 5 kilometrov. Koliko kilometrov preteče v enem tednu? Za začetek obarvajmo besedilo s podatki z modro barvo, besedilo z vprašanji pa z rdečo: Nika vsak dan preteče 5 kilometrov. Koliko kilometrov preteče v enem tednu? V zvezku besedilo težko obarvate (razen če ga prepišete ;) ), lahko ga pa podčrtate. Nato označimo nepomembne podatke oziroma podatke, ki ne vplivajo na izračun:
Pomembne podatke pa označimo z rumenim markerjem: Podatki iz modrega dela so torej:
Na tem mestu se lahko malo ustavimo in razmišljamo:
Tudi v rdečem delu imamo podatek:
Zopet razmišljajmo:
Sedaj pa si oglejmo neznanko iz rdečega dela:
Končni razmislek:
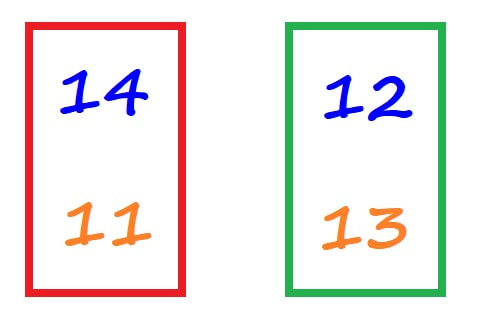
Končnega izračuna na tem mestu niti ne bom zapisal, saj namen zapisa ni rešiti besedilno nalogo, ampak omeniti možnost reševanja z vmesnim razmislekom. P.S. Dr'gač je pa rešitev 35, da se ne boste preveč tolk'l po glav' ;) Iz preprostega razloga - ker rezultat potem kar "pade pred nas" :) Oglejmo si naslednjo nalogo: V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj? Kdor "obvlada", bo hitro ugotovil, da mora sešteti 14 in 12. Kaj pa tisti, ki se še učijo oziroma imajo težave pri razumevanju? Pomaga že, če z barvami "opremimo besedilo ... V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj? ... še lažje pa nam bo, če situacijo skiciramo (poudarek je na "skiciramo", saj smo pri matematiki in ne pri LUM :) ) Sedaj, ko imamo sliko, bomo na vprašanja odgovorili veliko lažje. In to ne le na eno, tudi na kopico le-teh, recimo:
V oklepaju so barve, na katere moramo biti pri posameznem vprašanju pozorni. Tole je bolj "ziheraška" metoda, ki sicer lahko vzame nekoliko več časa, je pa zato dokaj pregledna. Razložimo jo na primeru: Pešec prehodi pot 72 metrov. Koliko časa hodi, če je njegova povprečna hitrost 2 m/s? Berimo tekst in si sproti zapisujmo količine, zraven pa njihove podane vrednosti oziroma vprašaj, če te vrednosti iščemo. V oklepaje dodajmo še oznake za te količine, da bomo v nadaljevanju lažje našli ustrezno enačbo.
V šoli se učimo, da morajo biti v izpisu zgoraj podane količine, spodaj (pod črto) pa iskane količine. To sicer lepo zgleda, ni pa nujno za reševanje naloge. Če želite, lahko zgornji seznam še vedno popravite: pot (s) = 72 m hitrost (v) = 2 m/s ---------------------- čas (t) = ? Odsvetujemo pa vam, da za vsako ceno skušate vzdrževati "pravilni" vrstni red podatkov že med samim izpisovanjem le-teh. To vas lahko samo še dodatno zmede. Če vse podane količine navedemo z osnovnimi enotami, se bodo na koncu enote lepo "ujele" in tudi količina, ki jo iščemo, bo v osnovni enoti. Količine, ki niso podane z osnovnimi enotami, pred vstavljanjem v enačbo pretvorimo. Pri tem si lahko pomagamo z desetiškimi potencami. Po pregledu količin, ki nastopajo v zgornjem izpisu, kaj hitro ugotovimo, da nas do rešitve pripelje naslednja enačba: Ker iščemo čas (t), bo enačbo potrebno obrniti. Nekaj navodil za to najdete tukaj. Lahko pa v enačbo preprosto vnesemo vrednosti, na mesto iskane količine pa zapišemo x: Ko x "rešimo" iz enačbe, ugotovimo, da je iskani čas enak 36 sekund.
Marsikdo ne mara vmesnega koraka, imenovanega "izpisovanje podatkov", zato naj vam predstavimo naslednjo metodo, kar na primeru: Kolesar s povprečno hitrostjo 12 m/s prevozi pot 36 metrov. Koliko časa porabi za to pot? Najprej opozorilo. Če želite uporabljati opisano metodo, morate vedno vse količine navesti z osnovnimi enotami! Če so le-te podane z drugimi enotami, jih je potrebno pred vstavljanjem v enačbo pretvoriti. Pri tem si lahko pomagate z desetiškimi potencami. Najprej pobarvajmo tekst. Del, ki se nanaša na posamezno količino, naj bo svoje barve. Količine, ki jih moramo izračunati, podčrtajmo. Te količine se ločijo od ostalih tako, da zraven njih ni navedenega številskega podatka. Kolesar s povprečno hitrostjo 12 m/s prevozi pot 36 metrov. Koliko časa porabi za to pot? Pomislimo, katera enačba bi bila primerna za to nalogo. Glede na obarvan tekst mora vsebovati naslednje količine (v oklepaju so oznake za te količine - tudi te si prikličimo v spomin, da bo enačbo lažje najti):
(Če morda niste med tistimi, ki ne marate izpisovati podatkov, si pa količine v zgornjih alinejah brez sramu zapišite kar na papir, zraven pa seveda še njihove vrednosti. Tak način je tudi nam najbolj všeč, saj je najbolj pregleden) Ko pobrskamo po glavi ali po zvezku, ugotovimo, da gre za naslednjo enačbo: Če nam obračanje enačb ne gre najbolje (komu pa gre :) ), lahko znane količine vstavimo že v njeno osnovno obliko, pa jo bomo potem obračali po mili volji. Neznano količino označimo z x. Da je delo še enostavnejše, lahko vstavljanjem količin enačbo zapišemo s svinčnikom in nato pišemo s krepkejšim pisalom kar čeznjo: Iz enačbe izrazimo x in dobimo iskani čas. Ta znaša 3 sekunde. O tem, kako do njega najlažje pridemo, pa si preberite tule ;)
|
Arhiv
December 2023
kategorije
All
|



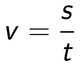
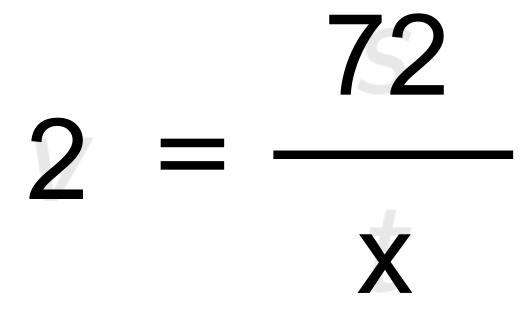
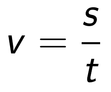
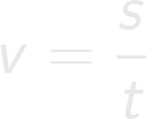
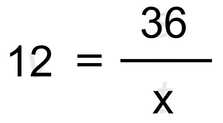
 RSS Feed
RSS Feed
